An Improved Active Shape Model Application onFacial Feature Localization

Published Online November 2010 in MECS

Facial feature extraction is an important process in facial image analysis. It can be used to face recognition and verification, facial animation, face image compression, etc.Important facial features include the face contour, eyes, eyebrow, nose, mouth, etc [1]. Many approaches have been proposed for the extraction of these facial features in recent years, and the highest attention has been given to active shape model (ASM) and active appearance model (AAM). The active shape model (ASM), proposed by Cootes and Taylor, has attracted much attention in different areas of feature extraction, such as for medical images, face images, hand gestures, etc. Because ASM captures the specific characters of a shape and its variations are denoted by a statistical shape model, it can therefore adapt to any predefined shapes more effectively and accurately.

Although original ASM algorithm can get good convergence results in many cases, it strongly relies on the position of initialization of mean shape model. When the mean shape model is far from the real face contour, it is prone to get a bad local convergence result. At the stage of searching for target points, the original ASM algorithm only uses the local gray profile model around landmark to ensure the accuracy of localization of feature points, which makes the localization result easily occur error. Besides, if the light condition of target images is largely different from that of training images, it will cause the built gray profile model can’t guide the move of feature points rightly, which makes the algorithm not converge, and the localization result of feature points not ideal, even localization failure. On account of those above defects, Du Chen introduced the edge information and part information of face to the matching process of ASM which improved the performance of ASM [2].Fan-yuhua used log-Gabor coefficients to describe the local texture distribution and built models for each feature point to increase the robustness to illumination change and other noises [3].

In this paper, an improved active shape model is proposed after deeply researching the original active shape model. The proposed algorithm includes the following four aspects. Firstly, this paper adopts a semiautomatic facial feature points marking tool. Adoption of the marking tool greatly reduces the burden of marking points. Secondly, this paper proposes an improved 2D texture model, which is based on Gabor wavelet coefficients and gradient feature. We propose to extract 2D gradient feature on the highest level and the higher level of multi-resolution pyramid images, and use Gabor wavelet transformation to extract the lowest level’s 2D local texture feature. This method makes facial feature points localization more accurate. Thirdly, we improve the multi-resolution pyramid’s decomposition method of the original active shape model. This paper proposes to use wavelet transformation to get pyramid sub-images. Finally, this paper modifies the multi-resolution searching scheme of the original active shape model. We change the length of 2D profile searching rectangle according to different pyramid levels in the proposed algorithm.

The organization of this paper is as follows. In Section 2, we provide a brief introduction of the original active shape model. Our improved ASM is introduced in Section 3. Experimental results and the performance comparisons are given in Section 4, and a conclusion is drawn in Section 5.

• II.    Brief introduction of the original active SHAPE MODEL

As a kind of statistical model, the original ASM algorithm includes three procedures: feature points mark, construction of the ASM, and localization of contour. The following gives a brief introduction of the original ASM [1] [4] [5] [6].

• A.    Feature Points Mark

The model-construction procedure of ASM requires marking n key facial feature points on each training image manually. N facial images are chosen, and each image is marked n feature points as training data manually. The marked feature points can be represented as the following vector.

X = [ x,_v...x_m , y_n,...У п Г i = 1,2... N (1) where ( x _j , y _j ) are the horizontal and vertical coordinates of the jth feature point of the th training image. T represents the transpose operation. The role of landmark points is controlling the shape of model contours. A typical setup in our system consists of 58 manually assigned landmark points ( n = 58). Fig.1 shows a training image with its landmark points marked. All the horizontal and vertical coordinates are arranged of a single group, and are matched with each other. Here, N represents the number of training images, and n represents the number of feature points of each image .Each X represents a shape vector.

Figure 1. Locations of the points used to represent a face

• B.    Construct on of The Act ve Shape Model

The model-construction procedure of active shape model is separated to the following two steps.

The first step: In order to make the shape model independent of the position, size and orientation of the face, we align these shape vectors by rotation, scaling and translation. The measure of the alignment is to minimize the sum of the squared distances of the feature points [6].

The second step: After the alignment, principal component analysis (PCA) is then applied to capture most of the shape variations. The PCA algorithm is as follows.

The mean of the shape can be expressed as

N

X = — yX/,             (2)

N £ and the corresponding covariance as

N

C = - Z ( X - X )( X - X ) T .        (3)

^N i = 1

The eigenvalues ( X 0 , X 1 , l X 2 _n - 1 ) and the corresponding eigenvectors ( p 0 , p 1 , L p 2 _n - 1 ) of the covariance matrix C, where X _i >  X _{i + 1} , can then be computed. Because the higher eigenvalues corresponding to eigenvectors contain much information of shape change, we can use some higher eigenvalues corresponding to eigenvectors to represent any shape vector approximately. We select the first j eigenvalues satisfying the following equation:

j        /2 n - 1

Z M Z ^k ^ t        (4)

k = 0    / k = 0

The determination of the value of t varies from different applications. Here, we set t be 0.98. The first j eigenvectors with the largest eigenvalues arranged in descending order can be formulated as P s = ( p 0 , p 1 , l p j - 1 ) .Therefore, a shape model can be approximated as follows:

X = X + P s b s ,               (5)

where b _s is a weight vector for the j eigenvectors ， referred to as the shape parameters ， which can be computed as follows:

When fitting the shape model to target shape, the value of b _i is constrained to lie within the range ± 3 ^[X-i ,where X i is the eigenvalue corresponding to the ih principal component, and X i match with b .This can ensure that this range of shape parameters can represent most of the shape variations in the training set.

a ccording to pca, X is the mean shape vector, and p is corresponding eigenvectors matrix. Any facial shape X can be represented as X = T_c (X + Pb) ,where c is geometry parameter, and b is shape parameter of PCA. Geometry parameter c includes the horizontal and vertical offset X _t ,Y_t ,the scale variable s and the angle

X t

Y t

x

variable 0 . T c can be represented as follows, which expresses the geometry variation of the shape.

s cos 0 — s sin 0"|Г x s sin 0 s cos0 J_y

+

T c

y

c = V , Y t , s , 0             (7)

Facial shape X is represented as a function, which is based on geometry parameter c and PCA shape parameter b. So, the problem of facial feature localization is changed to the problem of assessing the optimum geometry parameter c and the PCA shape parameter b.

• C.    Localization of Contour

ASM adopts gray match method which is based on profile. Its main idea is that we get the local texture feature around each feature point, which is the normalized derivative of the profiles sampled perpendicular to the feature point contour and centered at the feature point.

Given a point of ( x_j , y_j ) ,the sampling of l pixels on two sides of this point along the normal direction of the contour leads to the profile length being 2 1 + 1 .We use gray value to formulate the following vector:

^g ij = ^(g ij1 , g ij 2" .^g ij(2 i + 1) ) .                    ⁽⁸⁾

where g_ij represents the gray-level profile of the jth feature point of the ith training image, and g ijk ( k = 1,2...2 1 + 1) is the gray-level intensity of a corresponding pixel. The derivative profile of g_ij has a length of 2 l ,and is given as follows:

^dg ij = ( g ij 2 ^{— g} ij1 , g ij 3 ^{— g} ij2 ,".^g ij(2l + 1) - ^g ij2l ) . ⁽⁹⁾

To reduce the impact of illumination and contrast, we normalize the above vector, which is given as follows:

y j =

dgij

2 l

E Ы k=1

^where dg ijk = g ij ( k + 1) ^— g jk .So, ^{the mean} g^ray^-level profile of all the images at the jth feature point is represented as follows:

1N gj = N E gj.

The corresponding covariance is represented as the following formula.

1 ^N

G j = n E ⁽ g j - g j^⁽ g j - g j^     ⁽¹²⁾

The mean gray-level profile and covariance are the matching features of the feature point. We make the same sampling analysis of each feature point, and then we can get the statistical property of the whole contour. Those statistical properties have the distribution of Gauss function. We adopt the Mahalanobis distance measure to compute the difference between the new profile and the mean profile, which is defined as the following formula.

f ⁽ g si ) =⁽ g si - g i ) T G f¹⁽ g si ^— g i )      ⁽¹³⁾

ASM adopts gray-level profile of the contour to iterate. In each iteration step, the current model’s location and shape is changed by changing the PCA shape parameter b to finish the match of model and the test image’s contour.

Ш. The IMPROVED active shape model

ALGORITHM

• A.    Adoption of A Semi-Automatic Facial Feature Points Marking Tool

The ASM algorithm needs to be marked a number of training images manually at the training stage. Each training image should be marked a number of feature points. Thus, feature points marking becomes timeconsuming.

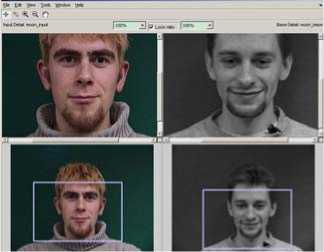
Figure 2. A semi-automatic facial feature points marking tool

Our adopted feature points marking tool has the following characters.

• ■ We can load two images at the same time. So, we can mark them at the same time.

• ■ We can mark feature points either on the first image or on the second image.

• ■    The marking tool has the function of position prediction of feature points. If we mark point on one of the two images, the corresponding point will occur on the corresponding image automatically. This function greatly improves marking efficiency. However, this position prediction function is based on the geometrical position of marked points, thus sometimes position prediction is not accurate enough and it needs us to adjust the position manually.

• ■ We can move and delete the marked points.

• ■ We can save the marking state, which allows us to mark the same image discontinuously.

Because the marking tool has the position prediction function, and the marked facial key parts (eyebrow, eye, mouth, face contour) usually have regular geometric shapes, the adoption of the marking tool can greatly improve marking efficiency and reduce marking burden.

• B.    The Modified 2D Texture Model Based on Gabor Wavelet Coefficient and Gradient Feature

The original ASM uses 1D gray profile of the feature point as the match feature, and its computation complexity is relatively low, but sometimes its localization accuracy is not high. Gabor wavelet coefficient can provide rich local-texture feature information and thus leads to accurate feature point localization, but with the drawback that it may add computation complexity. Reference [7] divided facial feature points into fiducial points and contour points. In that paper, the author extracted Gabor feature for fiducial points, and gray feature for contour points. Its localization accuracy was not high because only the 1D local texture feature was extracted and its feature expression method was relatively single. Reference [8] used gray and Log-Gabor feature to express local texture feature together. Though the author combined 2 different kinds of texture feature, he still extracted 1D feature and could not ensure high localization accuracy. In addition, extracting Log-Gabor feature for all the feature points added computation complexity.

According to the basic idea of multi-resolution pyramid searching strategy of the original ASM, in the upper levels of the pyramid, only estimated values for model fitting are determined. At the lowest level of the pyramid, the final model fitting values for the original images are computed. That is to say, a coarse-to-fine searching strategy is adopted. In the upper levels of the pyramid, the feature points are coarsely localized .And at the lowest level of the pyramid, the feature points are finely localized. So, we adopt the following two steps to build local texture feature model.

The first step: Extraction 2D gradient feature – The original ASM algorithm always builds local gray statistical property of feature points’ neighbor area .That is to say, the gray-level model is the normalized derivative of the profiles sampled perpendicular to the feature point contour and centered at the feature point. Experimental results show that to obtain sufficient statistical information needs a large number of training images if we extract gray feature as local feature. In addition, gray feature’s robustness to illumination is worse than gradient feature [8]. To reduce the influence of illumination to localization accuracy and reduce the number of training images, this paper proposes to extract 2D gradient feature on the highest level and the higher level of multi-resolution pyramid images, because gray feature is very sensitive to illumination and the number of training images is limited.

The details of profile extension from 1D to 2D can be seen in reference [8].A 2D gradient profile at a feature point is created in the following three steps: convolution, normalization, equalization [9]. These three steps are repeated at each feature point.

• ■    Convolution

In the convolution step, we move a 3 x 3 gradient mask over each pixel in the area around the feature point to generate a profile matrix. Each element of the profile matrix corresponds to a pixel. The gradient mask we used is as follows:

A = 0

- 2

We can get the gradient profile matrix by convolution. The profile matrix is two dimensional. We treat the profile matrix as a single long vector to get its mean value and covariance matrix.

• ■ Normalization

To eliminate the influence of illumination and contrast, we normalize the profile matrix by dividing it by the absolute sum of its elements.

• ■    Equalization

We equalize the normalized profile matrix by applying a sigmoid transform to each element x of the matrix. More details about the sigmoid transform can be seen in reference [8].

The second step: Extraction 2D Gabor feature – According to a coarse-to-fine searching strategy, this paper proposes to use Gabor wavelet transformation to extract the lowest level’s 2D texture feature of each feature point because Gabor wavelet coefficients contain rich local-texture feature information.

Gabor wavelet transformation has good space local character and orientation character. It can extract space frequency and local feature of muti-orientation in a local image area. Two dimension Gabor wavelet is shown as the following formula.

W ( x , y , 9 , Х , ф , о , у ) = e

X ^,2 + Y ² y '²                   ,

2               x'

• ^{2 0}  cos(2 n —+ ф)

X

where x' = x cos 9 + y sin 9, y' = - x sin 9 + y cos 9.

From (15), we can see that 2D Gabor wavelet is the convolution result of triangle function and Gaussian function. Equation (15) has five parameters which can control the 2D Gabor wavelet. The following will discuss these five parameters’ functions.

• 9 controls the orientation of Gabor wavelet, which makes the wavelet circumrotate around its center.

X controls the wavelength of triangle function, which determines the frequency of Gabor wavelet.

ф controls the phrase of Gabor wavelet, which is chosen as 0 and ^ 2 usually.

О controls the radius of Gaussian function, which determines the size of Gabor wavelet. It is usually proportional to wavelength.

Y controls the length and width ration of Gabor kernel.

Different parameters can generate Gabor wavelet with different shapes. We adopt five wavelengths and eight orientations in this paper, which is shown as the following formula:

includes phase difference. So, if there are two points with small displacement, then their phases vary largely. So, phase-sensitive distance function can measure difference of two points and can accurately localize feature points. So, we choose phase-sensitive distance to measure the similarity of two points in this paper. The displacement between two locations with small displacement can be approximately estimated by maximizing the phasesensitive distance S ф ( J , J ') in (19).If we want to

4 + i

X = 2 2, i = 0~4 3X о =—

in

9 = —, i = 0 ~ 7 8фе {п /4,-п /4}

Y = 1

maximize 5 ф ( J , J ') ,we can suppose

^{d s} Ф = ^{d s} ф

ddx   ddv xy

= 0 ,then

d(J,J')

Г d x )

d

V y 7

Г Г xx yy

( г

¹ yy

Г Г xy yx V

^Г xy

ryx xx 7

ГФ ^x ) v y 7

By this way, 40 Gabor coefficients in the complex form are used to represent the pixel and its vicinity. Specifically, a jet vector J is shown as follows:

Jet = (ax, фх, a 2Ф2,... a 40Ф40)Jj = aj exp(iфj)

Where a j . and ф j are the magnitude and phase of the jth Gabor coefficient. a j varies slowly, and ф j varies quickly.

We suppose there exist two points P and P' with relative small displacement, whose Gabor Jets are J , J ' .The similarity between two jet vectors is measured with the following two functions:

s a ( J , J ')

E a j a j

' E a ² E a

S ф ( J , J ') =

E a j a j 'cos( ф _j - ф _j '- dk j■ ) j    E « j ¹E «j'

where k =

2 n cos 9 X 2 n sin 9

X

Phase-insensitive distance function (18) doesn’t include phase parameter. If there are two points with small displacement, then their phase-insensitive distance is large. A range difference of the two jets can be determined. Phase-sensitive distance function (19)

If ГxxГyy - rxyГyx * 0 , where Ф x =E ajaj' kjx (ф- Ф'),

Фy = E ajaj ' kjy (Ф - Ф ') , Гxy = E ajaj ' kjxkjy .

and Г xx , Г yx , Г yy are defined accordingly. xx yx yy

Extracting 2D Gabor texture feature may add the computation complexity, but we only extract this kind of feature at the lowest level of pyramid images, so the computation complexity is not very high.

We can localize feature points accurately in the case that the computation complexity is not very high, since we effectively combine 2 different kinds of texture feature.

• C.    A Modified Multi-Resolution Pyramid Decomposition Method

At the training and searching stage of ASM on muti-resolution frame, original ASM algorithm adopts the following method to get pyramid images of training image. First, let training image pass a Gaussian filter, and then sample the filtered image in interval. The resolution of these images decreases gradually. The size of the latter scale image is half of that of the former scale image. The pyramid sub-images obtained by this method, whose fine feature will get less and less as the resolution decreases. So, it counts against extracting rich texture feature and influences the feature localization accuracy.

Wavelet transformation has multi-resolution character. It can extract rich information from images effectively and realize adaptation analysis of images. Using wavelet transformation to build pyramid images has many advantages [10].

• ■ Wavelet decomposition is non-loss focus change. Its direct frequency is smooth, which is good to implement image correlation.

• ■ Each layer of wavelet decomposition is constituted by a direct frequency weight and three detail weights. So we

can implement character match using these character weights.

• ■ Wavelet transformation has Mallat quick algorithm, thus its computation complexity is low and computation speed is fast.

When we choose wavelet decomposition to implement character match, we should consider the following problems: choice of wavelet function, decomposition level L.

• ■ Choice of wavelet function

The chosen wavelet function should satisfy the following conditions. @ Information of original image should be protected as much as possible in low frequency image .® Computation formula should be as simple as possible. It’s better to have corresponding quick algorithm to implement using hardware.

• ■ Determination of decomposition level L

Determination of decomposition level is relevant to the size of template image. Experimental and statistic results show that the size of template image shouldn’t be small than 8 x 8 when correlation match is implemented. When it is small than this size, its provided quantity of information is limited. Thus it is easy to get error matching result. In addition, the decomposition level shouldn’t be large. Many times low-pass filter will also lose information of original image, thus make matching result on higher level incredible. Usually, the maximum of decomposition level is 3 ~ 5 .s o , the value of decomposition level should satisfy the following formula:

L < min{log2 N/8,5} (21)

where N is the minimum of the width and height of template image.

According to the above rules and the size of training and testing images, this paper uses three levels to decompose the training and testing images. The adopted wavelet function is db1 wavelet. The decomposition results are shown in Fig.3.In Fig.3, picture (a) is the original ASM’s decomposition result, and picture (b) is our method’s decomposition result. In picture (a) and (b), there are the first level (the original image), the second level and the third level pyramid sub-images from left to right. We can clearly see that, the pyramid sub-images obtained by wavelet transformation contain richer information than that of original ASM as the resolution decrease gradually. Rich fine-information is good to extract rich local texture-feature and build stable textureprofile model, and thus increases the accuracy of feature points localization.

(a) Decomposition result of original ASM

(b) Decomposition result of our proposed method Figure 3. Multi-resolution pyramid sub-images

• D.    A Modified Pyramid Searching Strategy

In traditional ASM algorithm, the profile searching length is kept the same for different pyramid levels when multi-resolution scheme is adopted. In this paper, we set the first level (the lowest level) as the original image, the second level (the higher level) and the third level (the highest level) as pyramid sub-images obtained by wavelet transformation. At the multi-resolution searching stage, we first search feature points at the lower resolution, and then search at the higher resolution gradually. Experimental results show that displacement of feature point varies from different pyramid levels [11]. The lower the level is, the smaller the displacement is. Because we adopt a coarse-to-fine searching strategy, the displacement is very small when the new position of the feature point is near the target position. So, in our proposed algorithm, we change the length of the 2D profile searching-rectangle according to different pyramid levels. At the low resolution, we can get ideal match result of the whole contour because we ignore some details of image and our searching range is relatively wide. Correspondingly, at the high resolution, we may get good match result of local feature because we reduce our searching range. In our proposed algorithm, the length of profile searching-rectangle is reduced adaptively according to the decrease of the level. The value of the displacement of the first level is constrained. In our experiment, we set the profile length of the third level as m, m/2 of the second level, and m/4 of the first level. We set a threshold T for the displacement of the first level. If the value of the displacement is greater than T, it is set to be T.

This modified pyramid searching strategy strengthens the robustness of the algorithm, and the efficiency of the algorithm is improved to a certain extent because the computation complexity is relatively low at the low resolution.

At the searching stage on each pyramid layer, we need an algorithm to determine when we should search at the higher resolution level and when we should stop the whole searching process. In our experiment, we record the number of searched target points within the range of 50% of the 2D profile center. When the number of the points, which satisfy the condition, is 95% of the sum points (the number of marked feature points of the shape model), we can deem the algorithm converges at that level. Then we can search at the next resolution level .We will not stop searching until it converges at the corresponding level. When the algorithm converges at the last level (level 0), we can stop the whole searching process.

W . EXPERIMENTAL RESULTS AND ANALYSIS

Our experiment is based on IMM and ORL face database. We choose 200 images as training images. We choose 100 images as test images. All the images for training and test are neutral expression of frontal face. We mark 58 facial feature points for each training image manually. In this paper, we mark the feature points at the outer contour of face and the edges of each face component.

Usually, a large profile searching length is needed for robust initialization and good feature points localization. However, a too large profile searching length may make matching results worse because an inappropriate face shape can be considered as the original face shape. In addition, it may add feature points localization time if the profile searching length is too large. Based on above causes and according to the practical size of IMM and ORL face database’ face images, we test over and over again and finally set the 2D profile searching-rectangle length is 4 of the first level, 8 of the second level, and 16 of the third level. The displacement threshold T is set to be 1 on the first level.

• A.    Performance Comparison

To evaluate the performance of our modified ASM algorithm, we use two evaluation functions [11]. The first is the average error function which is represented as the following formula.

= — x —

Nn

E ave

Nn

EE abs (X(i, j) - pos(i, j))

i = 1 j = 1

where N is the number of test images, n is the number of feature points of each image. x ( i , j ) is the manually marked position of the jth feature point on the ith image, and pos ( i , j ) is position localized by the ASM algorithm.

The other one is average computation cost time function which is represented as follows.

1N

T ave =^ t .             (23)

N i = 1

where t_i is the cost time processing each image.

Tab.1 is the performance comparison result of our proposed ASM and the original ASM. From the comparison result, we can see that our proposed algorithm has greatly improved the localization accuracy and processing time compared with the original algorithm.

TABLE I .

COMPARISON PERFORMANCE OF THE MODIFIED ASM AND ORIGINAL ASM

Objective function	The modified ASM	Original ASM
Eave (unit: pixel)	2.09	4.67
T ave (unit:s)	1.87	3.45

• B.    Experimental Results

Parts of experimental results are shown in Fig.4.The group (a) is our proposed ASM algorithm’s localization results, and group (b) is the localization results of the original ASM.Obviously, we can see that our proposed algorithm has made great improvement on localization accuracy than that of the original algorithm.

(a) Localization results of our proposed ASM

(b) Localization results of the original ASM Figure 4. Localization results of ASM

To evaluate the robustness of our proposed ASM algorithm, we choose several images whose faces have small angular deflection and make experiments. Parts of experimental results are shown in Fig.5. From Fig.5, we can see that our proposed algorithm may fail to locate when faces have small angular deflection.

Figure 5. Some localization failure results

V . CONCLUSION

In this paper, a modified active shape model is proposed to improve the performance of the original active shape model. The proposed algorithm includes the following four aspects. Firstly, this paper adopts a semiautomatic facial feature points marking tool. Secondly, this paper proposes to extract 2D gradient feature on the highest level and the higher level of multi-resolution pyramid images, and use Gabor wavelet transformation to extract the lowest level’s 2D texture feature. Thirdly, this paper adopts a new method of decomposition of multiresolution pyramid. Finally, this paper uses an improved searching scheme of multi-resolution pyramid.

Experimental results show that our proposed ASM algorithm has made grate improvement on localization accuracy and processing time than that of the original ASM.However, because the training images are neutral expression of frontal face, so the experimental results also show that our proposed algorithm may fail when faces have small angular deflection. How to make the proposed W algorithm more robust of face’s angular deflection is an important direction for our future study.