An improved PSO algorithm and its application in seismic wavelet extraction
Автор: Yongshou Dai, Hui Niu
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 5 vol.3, 2011 года.
Бесплатный доступ
The seismic wavelet estimation is finally a multi-dimension, multi-extreme and multi-parameter optimization problem. PSO is easy to fall into local optimum, which has simple concepts and fast convergence. This paper proposes an improved PSO with adaptive parameters and boundary constraints, in ensuring accuracy of the algorithm optimization and fast convergence. Simulation results show that the methods have good applicability and stability for seismic wavelet extraction.
PSO, fourth-order, cumulant matching, seismic wavelet
Короткий адрес: https://sciup.org/15010222
IDR: 15010222
Текст научной статьи An improved PSO algorithm and its application in seismic wavelet extraction
Published Online August 2011 in MECS
Seismic wavelet extraction is the basis of seismic wavelet deconvolution, impedance inversion and the forward model [1].It can be divided into deterministic and statistical wavelet extraction methods for seismic wavelet extraction. The former limits the scope of application for requirement of reflection coefficient. But the latter just needs to assume it. Lazear proposed the mix-phase wavelet extraction methods based on fourth-order cumulant [2], which fitted four moments of wavelet and fourth-order cumulant of seismic data. It owns a higher accuracy and numerical stability of wavelet extraction by full use of seismic data cumulant. However, due to the unknown model parameters, it is more difficult to determine the scope of the initial model parameters, seriously affecting the searching efficiency of optimization algorithms.
Therefore, this paper combines the fourth-order cumulant matching with parameters identification methods. Then the optimization algorithms are used to search the best solutions. PSO is the new nonlinear optimization algorithm based on swarm intelligence. It is easy to fall into the local optima, which owns simple concepts and few parameters. It is used for wavelet extraction by simulation based on fourth-order cumulant matching, combined with ARMA model.
Manuscript received January 18, 2011; revised January 23, 2011; accepted January 27, 2011.
National Natural Science Foundation (No.40974072) and Natural Science Foundation of Shandong Province (ZR2010DM14))
-
II. ARMA MODEL OF SEISMIC WAVELET
Generally, the seismic trace y ( n ) is assumed to be a zero-mean stationary stochastic process, and is formulated as a convolution plus additive noise v ( n ) , often represented by the well known convolution model[3]:
-
l c + 1 - l nc
y(n) = h(n) * r(n)+v(n) = ^ h(i) r(n - i)+v(n) (1)
i = 1 - l „c
Where h ( n ) is the seismic wavelet; lc , lnc denote the lengths of causal and non-causal parts of the wavelet respectively; r ( n ) calls as the reflection coefficient ,which obeys the IID distribution; v ( n ) calls as the additive noise, independent of r ( n ) .
The following assumptions can be described from the above model [4]:
(1)Generally, the reflection coefficient series r ( n ) are zero-means [5], IID non-Gaussian process. The variance CT ^ <® and at least th order cumulant meets the condition | rkr | < от .
-
(2) v ( n ) is the environmental noise, which comes from instruments and the synthesis of multiple reflection noise signals. It is additive colored noise and a random process independent with, whose Gaussian components is much larger than the non-Gaussian parts.
-
(3) h ( n ) is the non-causal, mixed-phased seismic wavelet. The distortion of channel detector is characterized by its non-causal parts.
According to the real seismic wavelet which has limited amplitudes and length, the convolution model can be a finite non-zero part of the unite impulse response of ARMA model.
Expressed as follows:
y (n) = x (n) + v (n) (2)
Where x ( n ) is a stationary stochastic process of ARMA model, whose input is reflection coefficient series.
The ARMA model satisfies the following difference equation:
pq
Z aix (n - i) = £ br(n - i) (3) i=0 i=0
Where, p , q are respectively the order of AR part and MA part; The model impulse response corresponds the seismic wavelet h ( n ) shown in equation (1).
One character of cumulants is that even order cumulants are not zero, different from odd cumulants. So, it should be carried for seismic wavelet estimation by fourth-order cumulant. Under the assumptions and nature of cumulants, the fourth-order cumulant equation of seismic records can be expressed as follows by use of formula BBR.
C4 y ( t1, t2, t3) = r4 rm 4 b ( t1, t 2, t3) (4)
Where reflection coefficient series r 4 r are scalar quantities, which can be absorbed as a factor without the impact of wavelet form. It means that the wavelet can be estimated by calculating the fourth-order cumulant of seismic records because the fourth-order cumulant of seismic records is the product of reflection coefficient series and the fourth-order moment of the wavelet.Since higher-order cumulants are symmetric on its factors,the objective function can be established in the sense of least square error[5].
-
L T 1 T 2
ф = EEE [ C 4 У ( t 1, t 2, t 3 ) - m 4 b ( t 1, t 2, t 3)] 2 (5) T i = 0 т 2 = 0 T 3 = 0
Where C 4 y ( t 1, t 2, t 3) is the fourth-order cumulant of seismic records, m 4 b ( t 1, t 2, t 3) is the fourth-order moment of seismic wavelet, L is the length of seismic wavelet, ф is the objective function of seismic wavelet. When ф reaches its minimum, its corresponding variables are the estimated value of seismic wavelet.
The objective function is solved by the application of nonlinear optimization algorithms, which is a nonlinear, multi-parameter and multi-extreme problem. Through the study of optimization, an improved particle swarm optimization algorithm is applied to the ARMA model, improving the calculation efficient and accuracy of cumulant fitting optimization method.
-
III. PARTICLE SWARM OPTIMIZATION
PSO is the new nonlinear optimization method, proposed by Dr. Kennedy and Dr. Ebherhart of US in 1995[1].It originates from study of birds and fishes food searching behavior. The basic idea is that each particle searches the optimal solution through group collaboration and information sharing between particles. It has simple concepts, less parameters and fast convergence speed. But the accuracy of the algorithm has close relationships with parameter selections. Inappropriate parameters easily lead to divergent results. In optimization process of elementary PSO, particles may be beyond the range of effective solutions because there is no boundary constraint.
In the T-dimensional target searching space, there is a population of particles which represent N potential solutions of specific optimization problems. 5 = { x 1 ,x 2,..., xn } , x i = { x 1 1 , x 2,..., x t } , i = 1,2,..., n means a vector point of the ith particle in the T dimensional solution space. p i = { p i 1 , p i 2,....., p tt } means the optimal solution searched by the ith particle; P g = { P g 1 , Pg 2 , , P gt } , g = 1,2,..., n means the optimal solution searched by all the particles; v = { v i 1 , v. 2 ,..., v it } means the searching speed of the ith particle. Every particle adjusts itself to find the optimal solution by tracking pi and pg . When the two extremes [2] are found, the particle updates its velocity and position according to (1) and (2) [3].
-
IV. PARTICLE SWARM OPTIMIZATION
PSO (Particle Swarm Optimization) [6] is the new nonlinear optimization method, proposed by US Dr. Ebherhart and Dr. Kennedy. It has simple concepts, few parameters and fast convergence speed. But algorithm accuracy has close relationships with parameters selection. Inappropriate parameter selection easily leads to divergent results and decreased accuracy [7][8].
Mathematical expression of PSO is as follows:
ху (t + 1) = a v j ( t ) + c 1r1j ( py (t ) - x ( t )) + c 2 / 2 j (t )( P gi (t ) - x ij ( t)) (6) xtJ ( t + 1) = x^t ) + vti ( t + 1) (7)
to calls as the inertia weight, for speed control of next generation; c 1, c 2 call as the learning factors, which obey the uniform distribution within the range of [0,1] , t calls as the iterative number.
From view of physics, to v ij (t ) calls as the memory item, for better ability to expand the searching space; C 1 r 1 j ( P j ( t ) — x j ( t )) calls as the particle cognitive item ,for the optimal solution from its own experience; c 2 r 2 j ( pgi ( t ) - xj^t )) calls as the group cognitive item ,reflecting collaboration and information sharing between particles[4], [5].
The defects of elementary particle swarm optimization algorithm are as follows:
(1)Accuracy of the algorithm has close relationships with parameter selections. Value of inertia weight is between 0.2 to 1.5, values of c 1, c 2 are both 2 in normal conditions.
(2)The parameters of the algorithm are constants regardless of the specific optimization models and their iterative processes.
Test and optimize the four standard benchmark functions, which are generally used to test and compare the performances of algorithms [7].
(1)Sphere function:
f (x) = Z x-2 (8)
i = 1
- 100 ≤ xi ≤ 100 , min( f ( x )) = f (0,0,...,0) = 0
(2)Generalized Griewank function:
f(x)=∑xi2-∏(i)+1
4000 i=1
- 600 ≤ x i ≤ 600 , min( f ( x )) = f (0,0,...,0) = 0
(3)Generalized Rosenbrock function:
f(x) = ∑[100(xi+1-xi2)2+(xi-1)2]
i = 1
- 30 ≤ xi ≤ 30 , min( f ( x )) = f (0,0,...,0) = 0 (4)Generalized Rastrigin function:
f ( x ) = ∑ [ xi 2 - 10cos(2 π xi ) + 10]2 (11)
i = 1
- 5.12 ≤ x i ≤ 5.12 , min( f ( x )) = f (0,0,...,0) = 0
Sphere function is a nonlinear symmetric single-peak function; Griewank function is a rotated, variabledimensional function which cannot be separated; Rosenbrock function is the typical pathological and quadratic function; Rastrigin function is a typical complex multi-peak function with large number of local optimas.
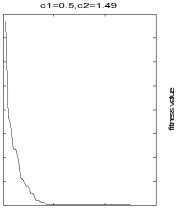
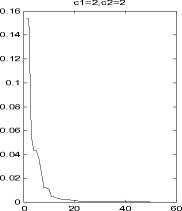
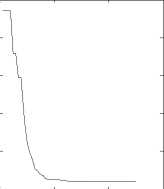
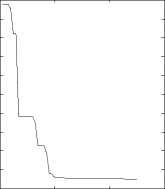
Conclusion: As it is shown in Fig.1 to Fig 5, different values of c 1, c 2 correspond different optimization results. The algorithms performances closely relate to parameter selections. Appropriate parameters determine higher accuracy of the algorithm, whereas accuracy will be reduced.
-
IV. Improved PSO
-
A. The core idea of improved PSO
For accuracy reduced of the algorithm because of improper parameter selections[8], this paper analyzes mathematical equation of elementary PSO. Inertia weight and learning factors increase or decrease linearly with the iterative process, so that the particles can search the entire space without falling into local optimum in the early period and find the global optimum in the end. Meanwhile, the improved PSO introduces differential mutation and random mutation, to increase the diversity of the particles group. At the end, this kind of PSO sets particle boundary constraints to ensure the effectiveness of solutions.
The improvements of PSO are as follows:
(1)Inertia weight
From the mathematical expression of PSO, we can conclude that larger inertia ensures a more effective global search of particles, smaller inertia weight means a more efficient local search. According to this theory, Shi and Eberhart proposed a strategy which inertia weight linearly decreases with the increase number of iterations [8].
Expressed as follows :
ω = ω max - k ∗ ( ω max - ω min)/ gen (12)
ω max calls as the maximum inertia weight, ω min calls the minimum inertia, gen calls the total number of
iterations for the algorithm, k of iterations for the algorithm.
w1=1.2
calls the current number
1.3
1.2
1.1
0.9
0.8
0.7
0.6
0.5
0.4
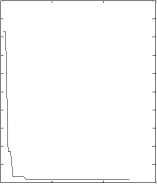
0 20 40 60
iterative number
c1=1.49,c2=1.49
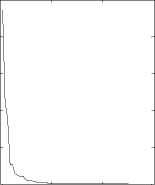
0 20 40 60
iterative number
1.4
w2=0.5
1.2
0.8
0.6
0.4
0.2
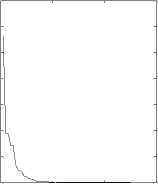
0 20 40 60
iterative number
Fig.1 Sphere function: different ω , same c 1, c 2
c1=2,c2=2
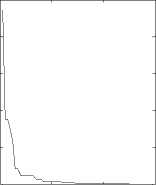
0 20 40 60
iterative number
Fig. 2 Sphere function: same ω , different c 1, c 2
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
iterative number
iterative number
Fig.3 Griewank function: same ω , different c 1, c 2
c1=0.5,c2=1.2

0 20 40 60
iterative number
Fig.4 Rosenbrock function: same ω , different c 1, c 2
c1=2,c2=2

0 20 40 60
iterative number
c1=0.5,c2=1.2
0 20 40 60
iterative number
0 20 40 60
iterative number
Fig.5 Rastrigin function: same ω , different c 1, c 2
(2)learning factors c1, c2 respectively represents the abilities of local extremes and global extremes search. Larger c1 and smaller c2 make the particles search extremes in the entire feasible space at early of the algorithm; Smallerc1 and larger c2 ensure the particles converge quickly to the global optimum value later.
Expressed as follows:
cl = cl start - k * (cl start - cl end ) / gen (13)c2 = c2start + k *(c2end - c2start ) / gen (14)
Where c 1 start , c 2 start call as the initial values for the learning factors, c 1 end , c 2 end call as the final values for the learning factors.
(3)Set the boundary constraints of particles.
When the position of the particle is beyond the given position, redefine the particle’s position using following formulas, to make sure that the particle is in the range of feasible solutions. At the same time, this redefinition ensures the diversity of new particles for undetermined boundary constraints. For papers published in translated journals, first give the English citation, then the original foreign-language citation [6].
-
B. Steps of improved PSO
Improve the elementary PSO and get the improved PSO flowchart (Fig.6). The implementation steps are as follows:
Step 5: Update the position and velocity of the particle according to (1) and (2). c 1, c 2 change linearly with the increase of iteration, which are no longer constants. Expressed as (8) and (9);
Step 6: Introduce the differential mutation, expressed as (10) after determining the particle’s best optimal position. Compare the particle mutated and those of before mutation. If better, replace x to xv .Or keep still;
Step 7: Introduction of the random mutation. This occurs on each particle with the probability p = 1/ T .
Step 8: If the particle’s position is beyond the given boundary, redefine the position of the particle based on (11) and (12);
Step 9: End the iteration when the PSO reaches its conditions (maximum number of loops or the requirement of accuracy of algorithm). Or transfer to step 2;
The improved PSO algorithm is used in standard test functions (Sphere, Griewank, Rosenbrock, Rastrigin).The optimization results are shown in Tab. 1 and Fig. 7 to Fig 10.
-
C. The core idea of improved PSO
The performances of algorithms are evaluated using the following standards: (1) Evaluation of convergence rates (2) Evaluation of stability and quality of convergence.
-
(1) Evaluation of convergence rate
The convergence rates of algorithms can be reflectedby
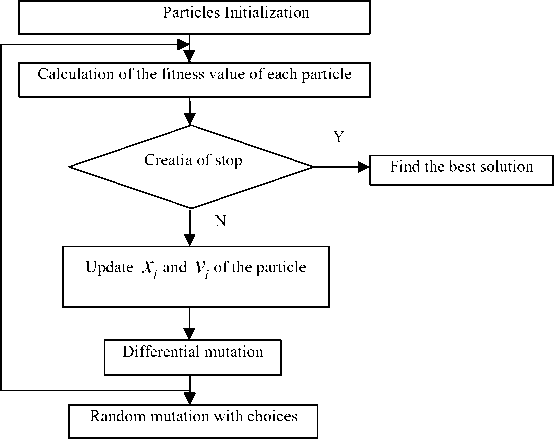
Fig.6 the flowchart of Improved PSO
test of average evolution generations. The average iterative number of elementary PSO is from 18 to 30 because of the advantage of “memory”. However, improved PSO owns more iterative numbers for the increase of calculation.
(2)Evaluation of stability and quality of convergence.
The indicators of evaluation are the average value which converges to optimal value and the average evolution generation. It is shown that the elementary PSO has poor local searching ability, low convergence rate and max error between the global optimal values. It can be seen that improved PSO improves the accuracy of the algorithm and stability of the global optimal value in Fig 7 to Fig 10.
-
V. STEPS OF SEIMIC WAVELET ESTIMATION
According to the objective function of seismic wavelet extraction and the improved PSO, the implementation steps can be summarized as follows:
Step 1: Data Generation: Synthesize the seismic data records by use of estimated ARMA wavelet model and random sequence which meet the assumption of reflection coefficient.
Step 2: Pre-parameter Estimation: Determine the order p , q of the estimated model and AR, MA parameters according to the above model identification methods.
Step 3: Determination of parameters search space: Based on the parameter estimates, determine the accurate searching range of model parameters.
Step 4: Fitting Optimization: In the searching space, find the optimal solution by using the improved PSO to estimate parameters of cumulants objective function.
Step 5: Analysis of Evaluation function: Calculate the evaluation function value; continue when it has a significant increase or decrease. Or go to step 7.
Step 6: Order Disturbance: According to the fitting errors, adjust the threshold of above method in order to generate a new set of p , q ; or go to step 3.
Step 7: End: Call the p , q before disturbance and precise model parameters as the optimal solution.
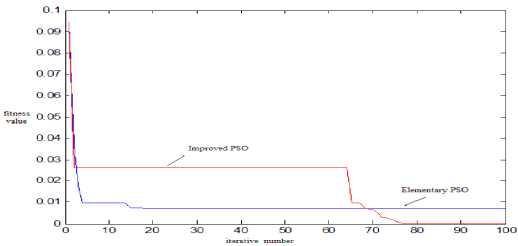
Fig.8 The iterative results of Griewank function based on different PSO
|
Test functions |
Algorithm |
Iterative numbers |
Optimal results |
Optimal solution |
|
Sphere |
Elementary PSO |
18 |
0.8052 |
0.2003 |
|
Improved PSO |
75 |
5.5412 × 10 - 10 |
1 × 10 - 6 |
|
|
Griewank |
Elementary PSO |
13 |
0.0931 |
0.1005 |
|
Improved PSO |
76 |
4.6103 × 10 - 11 |
6 × 10 - 6 |
|
|
Rosenbrock |
Elementary PSO |
25 |
1.1005 |
0.4201 |
|
Improved PSO |
45 |
0.5001 |
0.0793 |
|
|
Rastrigin |
Elementary PSO |
30 |
0.7643 |
0.1965 |
|
Improved PSO |
67 |
7.0703 × 10 - 5 |
0.0002 |
Tab.1 Optimization results of Improved PSO
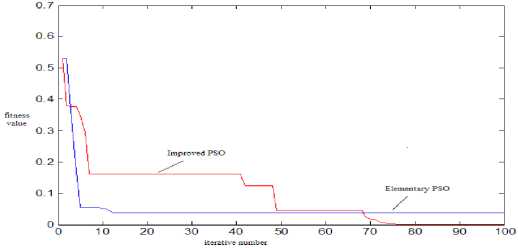
Fig.7 The iterative results of Sphere function based on different PSO
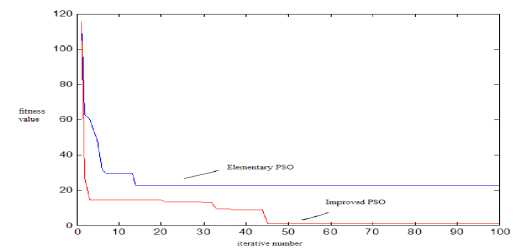
Fig.9 Iterative results of Rosenbrock function based on different PSO
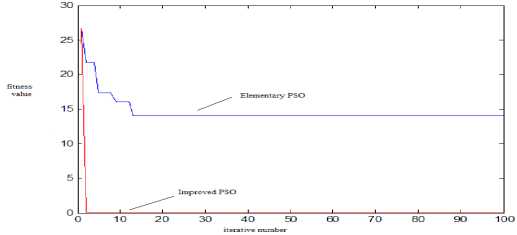
Fig.10 The iterative results of Rastrigin function based on different PSO
-
V. STEPS OF SEIMIC WAVELET ESTIMATION
Actual seismic wavelet is no causal, but the non-causal part is unknown and little by the introduction of detector and seismic records. It may cause further distortion of seismic wavelet if we artificially determine the non-causal components. So it is necessary to do in-depth study for causal seismic wavelet [9].
This paper will verify the effectiveness and practicality of this method by use of the synthetic seismic records. The coefficient series are independent and identically distributed (IID) random processes, which obey the Bernouli distribution;
The seismic wavelet is cause and mixed-phased, its differential equation of ARMA model can be expressed as follows: x ( t ) - 16 x ( t - 1) + 0.8 x ( t - 2) = r ( t ) - 0.8 r ( t - 1) - 12 r ( t - 2) (15)
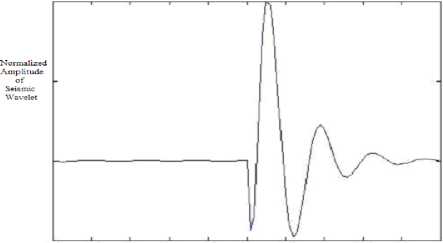
The zero-pole distribution of seismic wavelet ARMA model is shown in Figure 1.All the poles are in the unit circle, which proves wavelet is causal according to the wavelet classification standard; Similarly, one zero is in the unit circle while the other one is not, which proves that wavelet is mixed-phased. So the wavelet is causal and mixed phase. (wavelet waveform is shown in Figure 2).Noise in seismic records generally assumes to be Gaussian colored noise. If the seismic is expressed as y ( t ) = s ( t ) + v ( t ) , s ( t ) calls as the significant wave,
v(t) calls as the noise. The noise-signal ration can be defined as follows[10]:
v2(t)NSR = ∑ (16)∑ s2 (t)
Noise-signal ratio in the frequency domain is defined as:
1∫πAv2v (w)dw 1∫πRv2v (w)dw
NSR = 2 1 π - π π = 21 π - π π (17)
As2s (w)dw Rs2s (w)dw
2 π - π 2 π - π
Where Avv ( w ) , Ass ( w ) are respectively the amplitude spectra of noise and effective wavelet; Rvv ( w ) , Rss ( w ) is respectively the power spectra of noise and effective wavelet. In the paper, formula (17) is applied.
-
A. Influence of data length for ARMA model parameteres estimation
In the noise-signal ratio of 30%,the synthetic seismic records are generated with the length of 20000ms,10000ms,5000ms and 2000ms.The wavelet extraction results are as follows according to the above method:
Known as table 1 and figure 3,AR and MA parameters can get better estimates in long data case, which also meets the standard of E ( θ ) ≤ 4 But there is a certain bias between the estimated value and the actual value in case of short data(5000ms,2000ms).However, the wavelet waveforms have good continuity in different data length.
-
B. Influence of noise for ARMA model parameteres estimation
The synthetic seismic wavelets are generated with the length of 20000ms.For the study of the environmental noise impact, The seismic records are added with Gaussian colored noise with different noise-signal ratio as 10%,30%,50% and100%.Then the model parameters are estimated using the above method.
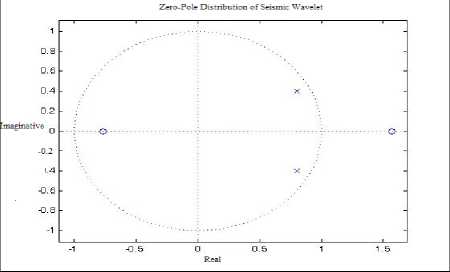
Fig.1 Zero-pole Distribution of Wavelet
О 10 20 30 40 50 60 70 00 90 100
Time t ins
Fig.2 the origin wavelet of synthetic seismic records
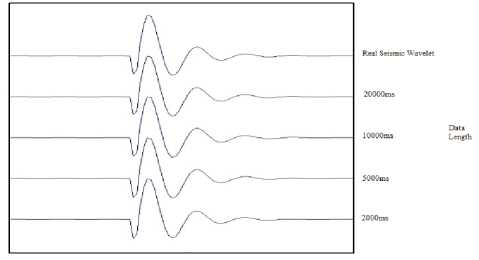
Fig. 3 The wavelets estimated with differen t lengths
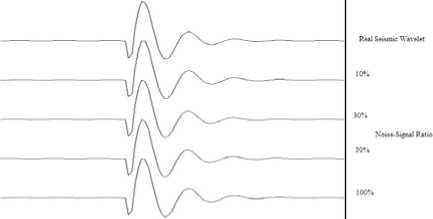
Fig.4 The wavelets estimated with different colored Gaussian noise
As it is shown in Table 2 and Figure 4, there is a slight increase in the parameters estimation errors with the noise increase. However, even the noise signal ratio is 1, the model parameters estimation still get good results. It is verified that the method used has good anti-noise tolerance for application in noise environment.
-
VI. CONCLUSIONS
In this paper, an improved PSO algorithm is proposed for the deficiencies of elementary PSO.
(1)The improved PSO has its superiority. The results of four standard test functions show more accurate performances of improved PSO.
(2)PSO is a new evolutionary algorithm based on swarm intelligence [7]. But unlike the in-depth research of genetic and simulated annealing algorithms, there are many issues to solve. For example, there must be strict theoretical proof about convergence and global optimality of PSO. Another focus will be how to combine PSO and other evolutionary algorithms, and establish the appropriate PSO model for different optimization problems.
(3)The use of optimization methods. Assuming that the seismic wavelet is causal and mixed-phased, simulation results show that the accurate model parameters can be estimated in different data length and appropriate noise environment based on SVD(singular value decomposition) method, Zhang algorithm, SVD-TLS ,cumulant fitting method and the improved PSO algorithm.
(4)The convergence stability and quality of the algorithm are improved using the improved PSO. However ,the iteration number is a little high as 80 or 100.Therefore,how to ensure the accuracy of seismic wavelet extraction and improve the optimization efficiency of PSO will be the focus for future research.
(5)The nest target is for non-causal and mixed-phased wavelet and seismic records optimization using the improved PSO. Then the optimal results can be compared with other optimization algorithms such as genetic algorithm.
Список литературы An improved PSO algorithm and its application in seismic wavelet extraction
- Enders A. Robinson and Sven Treitel, Geophysical signal analysis [M]. Prentice-Hall, Inc., Englewood Cliffs, N.J., 1980
- Lazear G D. Mixed-phase wavelet estimation using fourth- order cumulant[J]. Geophysics, 1993, 58, p.1042~1051
- Velis D R,Ulrych TJ. Simulated annealing wavelet estimation via fourth -order cumulant matching.Geophysics,1996,61(6):1939~1948
- Tang B,Yin C.Non-minimum phase seismic wavelet reconstruction based on higher order statistics.Chinese J.Geophys.(in Chinese),2001,44(3):404~410
- Dai Y S,Wei L,Huo Z Y .Research on wavelet extraction via linear equation approach based on higher-order cumulant.Journal of China University of Petroleum(in Chinese),2006,30(4):24~29
- Xian-Da Zhang, Yuan-Sheng Zhang. Singular Value Decomposition-Based MA Order Determination of Non-Gaussian ARMA Models. IEEE Transactions on Signal Processing, 1993, 41(8):2657-2664
- Zhang Xianda .A method for MA order determination of ARMA model[J].Autmation1994,20(1):83-87
- KENNEDY J,EBERHART C. Particle swarm optimization. Proceeding of IEEE International Conference on Neural Networks. Piscataway ,NJ:IEEE,1995:1942-1948
- KENNEDY J,EBERHART R C.A new optimizer using particle swarm theory[A].Proceedings of the Sixth International Symposium on Micro Machine and Human Science [C].Nagoya,Japan:IEEE,1995:3943.
- KENNEDY, EBERHART R C.A new optimizer using particle swarm theory[A].Proceedings of the Sixth International Symposium on Micro Machine and Human Science [C],Nagoya,Japan:IEEE,1995:3943M. Young, The Technical Writer's Handbook. Mill Valley, CA: University Science, 1989.


