An intelligent diagnostic system for identifying karst voids enclosed by layers with nano-cement mortar

Original article

In the construction of residential and industrial buildings, an analysis of the underground layers of the earth on which the object stands plays an important role. Due to poor-quality geological exploration of the earth’s surface, the problem of karst sinkholes is revealed during the construction of residential buildings and industrial buildings. The paper proposes to strengthen swampy and structurally unstable soils, preventing collapses during the construction and operation of facilities.

METHODS AND MATERIALS

Microsilicon was widely used after 1960 and at this time it is becoming in demand. However, this significantly complicates the process of preparing cement mortar, since, for example, additional technical equipment is required to introduce such an amount of solid, waterinsoluble substances into the mixture into the well. Nanostructured silica is a highly active cement additive containing ultrathin particles, the main component of which is represented by an amorphous modification of silicon dioxide. The increase in the strength of the material is explained by the small particle size, which contributes to the interaction with calcium hydroxide and a significant compaction of the material structure. This process helps to increase the mechanical strength of the cement material, and microspheres fill the space formed as a result of hydration [12].

It is found in [13–14] that after the introduction of nanosilicon into cement mortar (NCCR), the cement solidification time decreases with an increase in the amount of silica nanoparticles. Consequently, nanomaterials have a higher rate of hydration reaction compared to cement.

Protection against karst manifestations under the foundation in residential and industrial buildings that have already been built or recently put into operation is based on drilling wells in this zone and pumping a cement solution containing silica nanoparticles (NCCR) into the rock thickness. When the NCCR is introduced into the rock thickness in the karst formation zone, two layers arise: the upper one is a bearing layer and the lower one is an insulating layer that restricts water access to the karst from below. The first well is drilled obliquely to the upper transition zone of the geological layer prone to karst formation, and the NCC is introduced to a depth of about 10 meters to create a lower insulating and stabilizing layer. The second inclined well is drilled under karst voids, in front of groundwater, and a liquid solution of NCCR with a thickness of about 5 meters is poured. The third well, the control one, is drilled vertically until the upper support and the lower insulation come into contact. Between the upper and lower layers in the middle karst

layer, groundwater runoff channels arise from basins to discharge zones that support the natural hydrogeological regime of the karst layer layers.

As a result, the protective properties of the rock increase, the chemical and physical properties of the soil improve, the strength properties of the soil increase and the probability of landslides decreases.

The paper further proposes to investigate the gasliquid layers in the control well, which are located in a gaseous or liquid medium. These systems can combine the properties of both gases and liquids, creating unique characteristics such as high fluidity and small particle size. The study of hydrodynamic fields in the filtration of noncarbonated liquids is an urgent task that has a significant impact on the design and operation of wells.

MATHEMATICAL FORMULATION OF THE PROBLEM

The task of studying the temperature field during filtration of carbonated liquid is an important task in describing the movement of fluid in karst voids. This is due to the fact that karst voids contain a significant amount of gas, due to which, under certain external and internal factors, the upper layer may collapse.

The saturation pressure is equal to the reservoir pressure, therefore, during the movement of water in a formation with karst voids, degassing occurs. Under these conditions, the temperature drops both due to heat absorption during the phase transition and due to atmospheric thermal effects of the gas phase, and the flow of the liquid phase causes an increase in temperature. At low gas solubility, the formation heats up, and at high gas-liquid flows it cools down.

When the saturation pressure is lower than the reservoir pressure, two water flow options are possible. The first option is a single-phase flow that heats up due to the pressure in the well greater than or equal to the saturation pressure, accompanied by heating due to the Joule-Thomson effect.

If the saturation pressure is in the gap between the pressure in the formation with karst voids and the pressure in the well, then a bidirectional flow is realized. In an area where the pressure exceeds the saturation pressure P _s <  P <  P _h , a single-phase flow occurs, accompanied by heating. In an area where the pressure is less than the saturation pressure P _w <  P <  P _s , A bi-directional, oncoming flow of water and gas is realized, accompanied by phase transitions, and a high gas solubility coefficient cools the flow.

The physical properties of water and gas in karst voids differ both in the depth of the formation and horizontally, that is, the karst layer is generally anisotropic. But for simplicity, we believe that the karst layer is porous and the surrounding rocks are homogeneous in hydrodynamic and thermophysical properties. We also believe that

APPLICATION OF NANOMATERIALS AND NANOTECHNOLOGY IN CONSTRUCTION the permeable layers are located horizontally and are surrounded from above and below by impermeable rocks with a solidified solution of NCCR.

Picture 1 shows the geometry of the problem under consideration, where the inflow of carbonated water occurs to a well of radius r ₀ .

When solving the problem, we use a cylindrical coordinate system, the axis z which coincides with the axis of the well, and point z = 0 is located in the center of the karst formation (– h <  z <  h ), where h – the half-thickness (half-thickness) of the formation, and its thickness (or capacity) is equal to twice the half-thickness ( H = 2 h ). Thermophysical properties along the vertical axis (thermal conductivity λ _z and thermal conductivity a _z ) differ from the corresponding properties along the horizontal axis r (λ _r and a _r – accordingly). Assume that the pressure and temperature inside the formation do not depend on the angular coordinate φ. In the field of z <  h is impermeable rocks with thermophysical parameters are located (λ _{z 1} , a _z 1 , λ _{r 1} , a _{r 1} ), and in the field z < – h – with thermophy ^z sic ^z al parameters (λ _{z 2} , a _{z 2} , λ _{r 2} , a _{r 2} ).

In the area from the power supply circuit R _k up to the saturation radius r _s . A single-phase water flow is realized (on Fig. 1 – area I). Well pressure P _w is less saturation pressure P _s , achieved when r = r _s in formation – h <  z <  h , where r _s – saturation radius. Hence on the area r ₀ <  r < r _s there will be a two-phase flow of water and gas (in Fig. 1, this area is darkened, zone II).

Consider the energy equations of the carrier phase consisting of water, dissolved gas, free gas (pure gas) and the skeleton of a karst porous medium, transformed into one equation using a single-temperature approach.

The energy equation for the saturated phase is written as an equation with an index i . The value of index i = 1 corresponds to water, i = 2 – dissolved gas, i = 3 – free gas – gas phase:

qp/ 〃 ^ + ^^[grad T,-+ _&1gradP]-ms^^ 三=

=div^ms^gradT^-L^i+^^i-T^,        (1)

where L _i – specific heat of the phase transition i -th components, and q _i – volume density of the free gas source.

If we add up the formulas for the energy of all phases and components, making their temperatures equal, we get:

Z 例 SRG + (1 — 相) PoCo 臨 + Z Gq ， q (gradT + qgradP)-

-2>s ， P£Q ^ + 24% = div ^ms^^^-m)^ gradT . (2)

By converting, we get:

w        E«,.p,.c,.                 Z6PQ0

:+ Г----------------nVT + p--------------- ^vp -

Xms_iPic_i +(l-m) p_oc_o EmSiPa+Q-m) p_oc_o

屮 з ， 空+         =

E^zP^+Q-^PoCo 欠  Z 侬RS + (1-次)Po% div [z^s；% + (1 -根)九o) gradT

£W5,P,C,. +(l-W ) p₀C₀

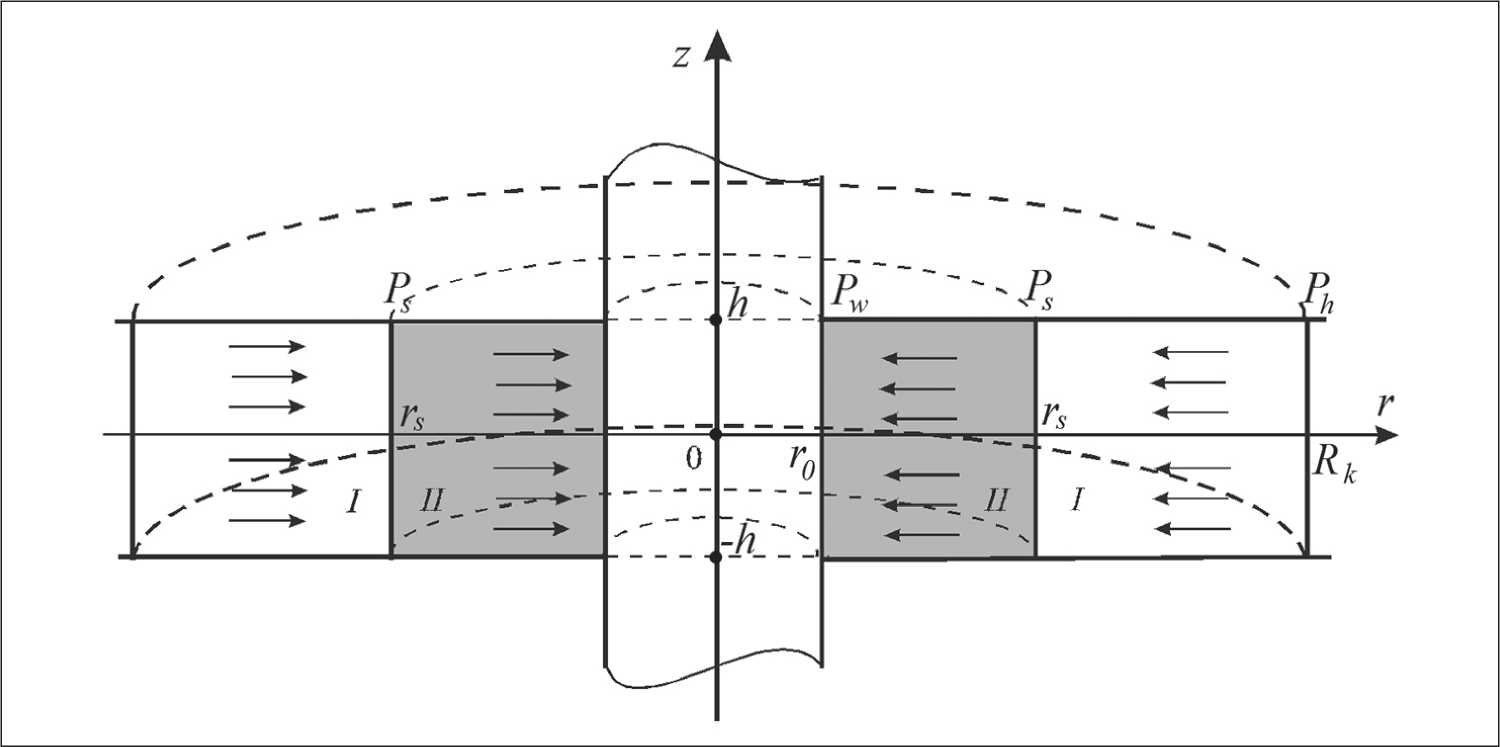
Fig. 1. Setting the problem

APPLICATION OF NANOMATERIALS AND NANOTECHNOLOGY IN CONSTRUCTION

This equation can be presented in a form corresponding to a single-phase flow equation with effective parameters:

If the consumption of carbonated liquid is equal i = 1, 2, 3, then, taking into account the equality of the filtration rate of water and the gas dissolved in it, we get:

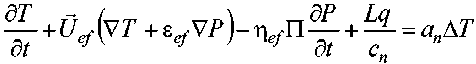
, (4)

where

汇服* P,£

□ = ^------,

一叫% +(1-加瓦 an=—-----------，

2 msiP£+(l 一 "%000

% = Х/и*Р№+(1 — т)РоСо ，

ε_ef – effective Joule-Thomson coefficient, и_ef – effective rate of convective heat transfer, η _ef – effective adiabatic coefficient.

The expression of the effective rate of convective heat transfer for a single-phase flow has the form:

и =_______ (С1Р1+С2Р2 ) О1+СзРз°з _______

” 叫 PiG+ms2P2c2+ 叫 Рз°з+(1-m)poCo'

%- 土[(。他 + C2P2 ) 出 + езрз ■[《• (9) e J          Hi       r3 」办

For a homogeneous isotropic porous medium for the effective Joule–Thomson coefficient, substituting, we obtain

Ejucq?

〜：    .

2 決科

If you express υ _i , then we get:

»>ср/ ( 5 ) Лч

.

%=」 . (5)

In an isotropic homogeneous medium, the vectors и ef and и _i are collinear, since they obey Darcy’s law, they thus coincide in direction with the pressure gradient:

In [4–13], it was shown that the value of the effective Joule-Thomson coefficient clearly does not depend on the permeability, pressure gradient, and heat capacity of a porous medium.

Consider the flow of carbonated liquid at i = 1, 2, 3, given the equality of the filtration rate of water and the gas dissolved in it, we obtain:

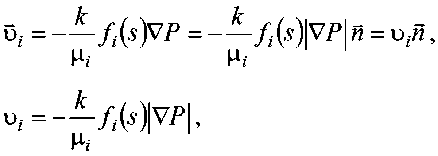
(呼问+脏 2P2 ) 5+£3 吃 3p3 ( С1Р1+С2P2 ) 5 +U3C3P3

where п – the unit vector in the direction of the pressure gradient.

If you convert the filtration rate formula i -th the phases in the formula for the effective convective heat transfer rate, we obtain:

U_ef= ^к ^^CiPifi^P\.n .             (7)

The rate of convective heat transfer and the rate of phase filtration for a one-dimensional flow are also co-direc ti onal and directed along the axis r , that’s why и _i = υ _i J r , и _ef = U_{ef r} , we get:                                    ⁱ

The heat capacity of the karst layer of the formation is determined by the expression

凄=加 S1PG + 例 S2P2s + 初 S3P3C3 + (1 —例 )po^co. (13)

When filtering carbonated liquid, the corresponding expression for the adiabatic coefficient is represented as:

XPE1 +S2P202^rl2 +S3P3C3% S1PQ+S2P2c2+S3P3S

Theoretical and experimental studies of temperature fields during filtration of liquid and gas in a porous medium were carried out by A.I. Filippov, M.R. Minlibaev, E.M. Devyatkin, P.N. Mikhailov and others in 1980– 2015 [8–14]. In the works of V.V. Dryagin, Ya.R. Adiev, A.A. Shilov, V.N. Fedorov, V.M. Meshkov, A.S. Bochkov, A.M. Sharipov, A.A. Sadretdinov, and others, temperature zones are taken into account during joint filtration of water and carbonated liquid [12–25].

APPLICATION OF NANOMATERIALS AND NANOTECHNOLOGY IN CONSTRUCTION

The formula for the effective Joule–Thomson coefficient for filtering carbonated liquids is as follows:

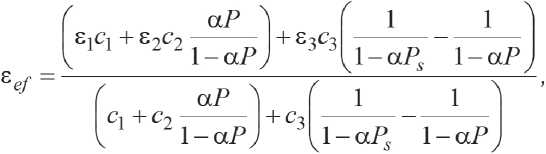
_ qq+e2c2g3+ 与 e3 3

²  1—a% 1—a 尸’ з i—aP

Due to the lack of degassing at high saturation pressures, the Joule-Thomson coefficient for filtration of carbonated water is as follows:

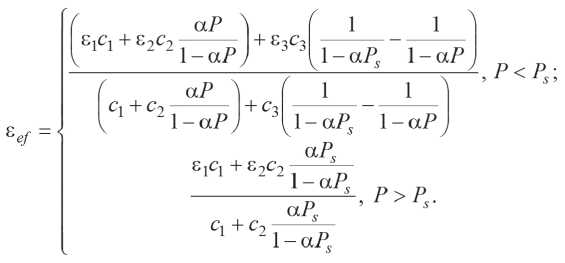
The formula for the effective Joule–Thomson coefficient of pressure has the form:

七 1 ( P£7 + P202^rlаНЬРзСзПз p .

OM + p2c2 )     '    "

PE% + P2c2n2 p

P1G+P2c2  ' S'         (17)

The effective rate of convective heat transfer is written as:

Р15 ( С1+С2^з ±£^1Ж±Ы

机 P 《 1 ( Q + С? 己 з ) + mg Р3С3 己 2 + (1 - 机 Во/ 化 1 + 己 2 )'

尸

RESULTS

aPs

Pi°i с*2

i 一叫

小 P1

+ (1-/и)росо

，尸＞巴•

In Fig. 2, curve 1, it can be seen that the temperature in the range –1 <  z < 1 is constant.

The first decomposition coefficient in this range takes both negative and positive values (curve 2). To correct the correctness of the solution, we add the zero and the first approximation of the temperature distribution (curve 3), which is expressed as a function of the temperature field on z . Figure 2 shows that in the central part of the formation, for short times, the zero approximation describes the temperature distribution with a disadvantage, and at the edges of the formation with an

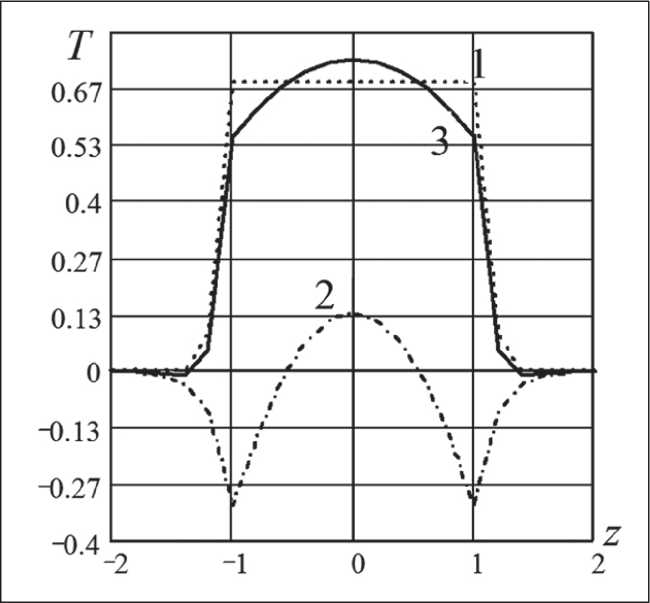
Fig. 2. Graphs of the dependence of dimensionless temperature T from the coordinate z in dimensionless coordinates: h = 1 м , R _k = 50 м , t = 0.01; ε = 0.25

excess. In environments, the zero approximation always gives an excessive temperature value.

DISCUSSION

By installing a permanent automated monitoring system for motion sensors, pressure and temperature of liquid and gas in karst voids on the control well, we will be able to monitor the dynamics of the main hydrodynamic parameters of karst voids, allowing us to assess the current regime of karst voids and, if danger arises, signal this.

Thus, using mathematical dependencies and data from the continuous monitoring system, we will be able to determine porosity, moisture content and gas content in the intermediate layer with karst voids.

CONCLUSION

The use of nanosilicon-cement mortar in the lower and upper layers allows:

– to increase the protective properties of rocks during karst phenomena;

– improve the reliability of the physical, chemical and bearing properties of the soil;

– to increase the strength characteristics of the soil;

– reduce the likelihood of emergencies:

– automate the technological process of hydrodynamic research in karst environments.

The addition of silica nanoparticles to the cement mortar changes the rheological properties of the mortar, affecting its viscosity and fluidity. This can improve filtration through porous materials. The presence of

APPLICATION OF NANOMATERIALS AND NANOTECHNOLOGY IN CONSTRUCTION

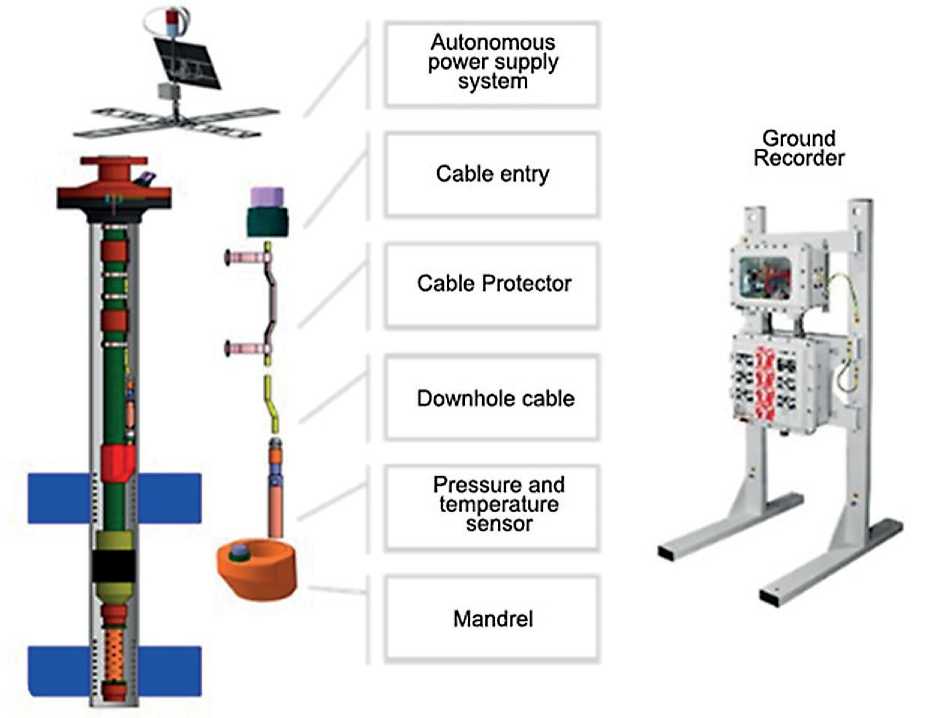
Fig. 3. Continuous monitoring system

gases in the liquid creates an additional lifting force effect and changes the flow behavior, which affects the pressure and filtration rate. A channel is formed between the dominant layer of the rock strata and the insulating stable layer for groundwater flow from the catchment area to the discharge zone, while maintaining the natural hydrogeological conditions of the rock strata, including the presence of water in the karst formation zone.

The advantages of using this development in construction:

• •    Consideration of hydrodynamic fields will help to design more stable foundations and structures, avoiding possible subsidence or destruction.

• •    Using nanotechnology to create sensors that will track changes in hydrodynamic fields and soil properties.

• •    The design of foundations taking into account the filtration properties of carbonated liquids to prevent subsidence and destruction.

The problem of filtration of carbonated liquid in karst voids is investigated. The resulting equation is used to calculate and analyze the spatiotemporal temperature distribution over time during filtration of carbonated liquid in karst voids. The study of hydrodynamic fields in the filtration of non-carbonated liquids is an urgent task that has a significant impact on the design and operation of wells.