• 1. Problem Statement

Consider for x = (х 1 ,Х 2 ,Х з ) € R ³ , t G R , X 3 > 0, the integro-differential equation

∂2u 3 ∂            ∂u t            3 ∂∂u d2 = Xdx- a(x2’x3)dx- + J k(xi,t —T)ьdx- a(x2,x3)dx   (x,T)dT(L1)

j=1                          0

under the following initial and boundary conditions u |t<0= 0,(1.2)

• ^# The study was performed with the support from the Russian Science Foundation, project no. 23-27-00264, https://rscf.ru/en/project/23-27-00264/ .

• (0 2024 Tomaev, M. R. and Totieva, Zh. D.

  a(x2 ,0)

  
  

  ∂u

  — (x,t) +   k(x i ,t

  
  

  - T )-— (x,T ) dT дхз

  
  

  X 3 =+0

  
  

  -8(xi )6(x2)6 ‘ (t),

  
  

  (1.3)

  
  

u(x,t) is the displacement function, а(х 2 ,х з ) is the velocity of propagation of transverse elastic waves, k(x i ,t) is the memory function showing the viscous properties of the medium; 8( - ) is the Dirac delta function, 8' ( • ) is the derivative of 8( - ) .

The direct problem is to find the function u(x,t) from equation (1.1) under the initial and boundary conditions (1.2), (1.3).

The inverse problem: to determine the function u(x,t) coefficient а(х2,хз) and the memory kernel k(x i ,t) , t >  0, if additional information is known

F x i ,X 2 [u](x 3 ,t, v, А) | х з =+0 = g(t,v,A), t> 0, v,A G R ,                (1.4)

where g(t,v, A) is the measurement data and

∞

F X 1 ,X 2 ^{[ u ]( x} 3 ,t^,V,

A)=/

u(x, t)e ^{i ( vx} 1 ^{+ x}x ² ) dx1 dx ₂

---------------------I

∞

is the Fourier transform of the function u(x,t) by variables x i , X 2 (next, i is imaginary unit).

Definition. A pair of functions а(х 2 ,х з ) G ( R ^x [0, от )), k(x i ,t) G ( R x [0, от )) is called the solution of the inverse problem (1.1)–(1.3) if the solution of the direct problem (1.1)–(1.3) u(x, t) from the class of generalized functions D ' ( R + x R ) satisfies (1.4) for g(t, v, A), belonging to the class D ' ([0, от )) for a fixed nonzero (v, A) .

The problems of determining the kernel of the integral convolution operator is a trend in the theory of inverse problems that arose at the end of the last century [1–8]. A more detailed analysis of the sources is presented in the monograph [9], which is one of the latest fundamental works in the theory of inverse problems for equations of memory type. It presents the results of a study of the well posedness of one-dimensional and multidimensional inverse problems for hyperbolic integro-differential equations of memory type. Theorems on the unique solvability of the inverse problems are proved, and stability estimates are obtained. Among the first results on inverse problems of linear viscoelasticity (close to this) can be noted [5, 10, 11]. In [5], the local solvability and global uniqueness in the one-dimensional inverse problem of determining the kernel of the integral convolution operator of the viscoelasticity equation with constant coefficients are obtained. In this paper, the direct problem is the Cauchy problem with continuous data. The inverse problem is replaced by a system of Volterra integral equations of the second kind. In [10, 11], the method of separation of variables is used to solve inverse problems in a limited domain, by which the problems are reduced to a system of integral equations of the Voltaire type with respect to unknown functions depending on a time.

The further results of research, in particular, over the past ten years is shown, for example, in [12–29]. In [12–17] there are inverse problems on the determination of kernels having a special structure. The goal is to reduce the initial problem to solving problems of integral geometry using a singular source (delta function) of wave disturbance. The unknowns to the inverse problems are the coefficients of the equation and the spatial parts of the kernel. In articles [18, 19], the main results are the global unique solvability of one-dimensional inverse problems using spaces of continuous functions with a weighted norm. In recent years, there has been an increasing of the number of publications on numerical calculations of the integral operator kernels [20–24].

Of most interest are multidimensional kernel determination problems when the unknowns depends on two or more variables. The multidimensional inverse problem for (1.1)–(1.3) and additional information (1.6) have been investigated in [25]. In this work, based on a combination of the method of scales of Banach spaces and the method of weight norms, a global unique solvability of the problem of determining the kernel of k(x, t) in the class of functions analytic in the variable x and smooth in the variable t was obtained.

In [26], the problem of determining the two-dimensional kernel of an integro-differential equation in a medium with weakly horizontal inhomogeneity is considered, in which method from [27] is developed.

Among the works devoted to coefficient inverse problems for viscoelastic media, which also determine the kernels of integral operators, one can note the works [28, 29]. For example, in [29] the one-dimensional problem of simultaneous determination of the wave propagation velocity and the kernel of the integral operator was studied. It is shown that both unknowns are uniquely determined by setting the Fourier image for the spatial variable of solving a direct problem on the boundary of a half-space. A conditional assessment of the stability of the solution of the problem is established.

The fundamental difference from the above results and at the same time the significant novelty of this work is the fact that it presents a multidimensional inverse problem of simultaneously determining the coefficient of the viscoelasticity equation and the kernel of the integral operator describing the properties of a viscoelastic medium for a half-space.

It should be noted that simultaneous recovery of several parameters for media with aftereffect is undoubtedly an actual problem from the point of view of applications, since it becomes possible to analyse the influence of the memory of the medium, for example, on the velocity of wave propagation in space. For practical applications, it is more interesting when the characteristics of the environment depend on two or more variables. For example, for geophysics, one of the main problem is the quantitative assessment of horizontal inhomogeneities in the velocities of seismic waves [30].

In this paper, which is a continuation of the study presented in [31], a new approach to the simultaneous determination of parameters depending on two variables in the viscoelasticity equation for a half-space is proposed. The novelty of the approach lies in the assumption that k(x i ,t) , а(х 2 ,х з ) weakly depend on the horizontal variables x i , X 2 as follows:

a(x 2 , х з ) = a o + ех 2 а 1 (х з ) + O(e ² ), k(x1,t) = ko(t) + Ex1k1(t) + O(e ² ),

(1.5)

where ε is small parameter.

In the equations (1.5) a 0 is a given positive constant.

The main purpose of this work is to construct a method for finding ko(t) and а 1 (х з ) , ki(t) with an accuracy of O(e ² ). To do this, as we will see later, it is enough to set the g(t, v, A) for two different non-zero sets (v j ,A j ) , j = 1, 2 .

The necessary and sufficient conditions for the global unique solvability of the inverse problem (1.1)–(1.4) and its stability estimate represent the theoretical significance of the work.

The theoretical results are useful for applications in solving seismic problems and the numerical implementation of this study. It has been shown [32] that with an increase in the strength of an earthquake, the soil behaves not as an elastic, but as a viscoelastic body. Soils are medium with memory, that is, the state of such medium at the current time depends on the entire background of the process. This is indicated, for example, in [33], which provides a detailed review of studies to clarify the nature of absorption of seismic waves in soils and examines the main patterns of absorption of stress waves in dispersed and semi-bedrock. As shown in [34], failure to take into account the absorbing properties of the medium leads to significant distortions in the restoration of the velocity model of the medium. The author is going to make a numerical analysis of the effect of the memory function on the wave propagation in half-space later. The algorithms given in the monograph [35] are also the basis for numerical analysis.

We seek the solution to (1.1)–(1.3) in form of the series in powers of ε

∞

u(x,t) = ^^Ej U j (x,t).

j =0

(1.6)

Using (1.4) and (1.6), we have

FX11X2 [u](x3,t,v,A)l x3 =+0

∞

=: U(xi,X2,t) = ^E ^j U j (xi,X2,t).

j =0

It is not difficult to verify that u j (hence U j ) are even in x 1 , x 2 for even j and odd for odd j . Thus, according to the well-known function U(xi,X2,t) , Uo(xi, X2,t) and Ui(xi, X2,t) can be found up to O(e ² ) [27]:

U 0 ( x 1 , x 2 , t ) =

U (xi ,X 2 ,t) + U (-Xi, - X 2 ,t)

Ui ( xi , x2, t ) =

U(xi,X2 , t) - U ( - X i , - X 2 ,t)

Since the method presumes determining a i (x 3 ) , k o (t) , ki(t) with accuracy O(e ² ) , by inserting (1.8) and (1.7) in (1.1), we obtain two inverse one-dimensional problems of the successive definition of k o (t) and a i (x 3 ) , ki(t).

(i) The problem of determining k o (t) and Uo(x,t) from the equalities

1 d ² u o = Г d ² u o + d ² u o 1 + d ⁽ du o \ a 0 ∂t ²       ∂x ²₁     ∂x ²₂      ∂x 3 ∂x 3

t

⁺ f ^{k o (} t - ^T ’ [[ W⁺W 1⁺ дХ з ( dX 3 )]^{( x}’^T ’^dT-

(1.7)

a 0

u o | t< o = °,

(1.8)

t

|^{U o} (x,t) + [ k o (t - т )lu l ( x,t ) dr

∂x 3                   ∂x 3

-5(xi)5(x2 )5 ‘ (t),

(1.9)

x 3 =+0

• (ii)    The problem of determining а 1 (х з ), k i (t) and — i (x,t) from the equalities

  ∂ ² u 1 ∂t ²

  
  

∂           ∂u 0      ∂u 1       ∂           ∂u 0

= L k o , -— X 2 a i (x 3 ) a-- + a 07—   + 7— X 2 a i (х зЬ—

∂x 3           ∂x 3      ∂x 3     ∂x 2           ∂x 2

+

∂ ² u 1

∂x ² ₁

+

d ² u1

∂x ² ₂

∂ ² u 0

^{+ x} 2 a i ^{( x} 3 ) dx 2

t

+ J X1 к1(т ) ^0 [

∂ ² u 0

∂x ² ₁

∂ ² u 0      ∂     ∂u 0

⁺ d 2 ⁺ ... V⁰ dX3^ x)'

u i | t< o = ⁰ , t

L[k o ,X 2 a i (+0)|u ° + a o|—1] + a o x i [ k i (t — т )|u ° (х,т) dт ∂x 3      ∂x 3                    ∂x 3

F x i ,x 2 ^{[ u} 1 ^{]( x} 3 , t, ^v, ^{А ) |} х з =+0 = F x i ,x 2

= 0, х з =+0

[U i ](t, v, A) =: gi(t,v,A) t> 0.

• (1.11)

• (1.12)

• (1.13)

• (1.14)

2. The Problem of Determining ko(t) and uo(x,t)

Introduce the variable z by the formula

x 3

z := ^=, c o := Vao • a 0

Let

v(z,t,v,A) := F _X i ,_X 2 [uo](coz,t,v,A)

t

Then

w(z, t, v, A) :=

v(z,t,v,A)+ У ko(t — т)v(z,T,v,A) dT exp (-ko(O)t/2) .

t

v(z, t, v, A) = exp ( k o (0)t/2 ) w(z, t, v, A) + У ro(t — т ) exp ( к о (0)т/2 ) w(z, т, v, A) dT, 0

t ro(t) = —ko(t) — У ko(t — т)ro(т) dт.

We obtain the following equations for the functions w(z, t, v, A) and r o (t) :

_∂ 2 _w

∂t ²

t

_∂ 2 _w

= -—77 + H(v,A)w —    h(t — т)w(z,т,v,A) dT,  z> 0, t G R,

∂z ²

∂w ∂z

z =+0

w | t< o ^ 0,

— c o C‘(t) — 2r o (0W)) ,

• (2.1)

• (2 . 2)

• (2 . 3)

• (2 . 4)

• (2.5)

t w|z=+0

= go(t, v, A) + У ko(t - T)go ( t, v, A) dT, 0

(2.6)

H ^{( v}, ^a) := —^{( v 2} +^A 2 ^{) c} o + 04) - r o (°),

h(t) ^: = r 0 ‘ (t)exp(r o (°)t/2) , go(t,v,A) := F _{X 1} ,_{X 2} [g o ](t, v, A)exp(r o (°)t/2), ko(t) := k o (t) exp (r o (°)t/2) .

Here, for example, r'o , rQ mean the operations of one-time and double differentiation. The derivative of the transformation parameter will be denoted, for example, g _v (t,v,A~).

We used the equality k o (°) = — r o (°) in (2.5) which results from (2.2).

By the theory of hyperbolic equations, the function w(z,t,v, A) , as a solution to (2.3)(2.5), possesses the property w = °, t < z, z >  ° , and has the following structure in the neighbourhood of the characteristic line t = z :

w(z, t, v, A) = —5(t — z) + w(z, t, v, A)0(t — z),                     (2.7)

co where w(z,t,v, A) is a regular function. Then go(t, v, A) := — 5(t) + go(t, v, A)0(t), go(t, v, A) := goo(t, v, A) exp(ro(°)t/2), co here goo (t, v, A) is the regular part of go (t, v, A).

Inserting (2.7) in (2.3)–(2.6) and using the method of separation of singularities, we find that w(z, t, v, A) satisfies the following equations for t > z >  ° ( w = w for t >  z ):

d^w dt ²

(2.8)

—+ H(v, A)w--h(t — z) — I h(t — t)w(z, t, v, A) dT, dz2                 coJ

z w|t=z+o = — 1— (ro(°) — H(v,A)z) := e(z,v,A),(2.9)

2 c o

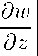
(2.1°)

t w|z=+o = go(t, v, A)+ / ko(t — t)go(t, v, A) dT +--ko(t).              (2.11)

c o

o

Thus, the inverse problem of determining k o (t) and u o (x,t) from (1.7)-(1.10) reduces to the problem of finding k o (t) and w(z,t,v, A) from (2.8)-(2.11).

Next we will find unknown quantities t q (°) , r 0 (°).

We will require continuity of functions w(z,t, v, A) , (d^z) (z,t,v, A) for z = t = ° and from (2.9), (2.11) we find:

r o (°)=2c o g o (°,v,A),                               (2.12)

^r 0 ⁽ °) = ^{— q (} °) + ^{( v 2} + ^{A 2 )} c ^{2 — c 2 g} o ⁽ °^{, v}, ^{A ) — 2 c} o ^g)‘o ⁽ °, ^v, ^{A )} .               ⁽ 2. ¹³⁾

For the last equalities, we used the relations

t k'(t) = —r'(t) — r(0)k(t) — У r'(t — r)k(r) dr, r2(0) k'(0) = -r‘(0) + r2(0),   k'(0) = —(— - r‘(0).

Next, note the r(0) , r ‘ (0) are already known. The following equalities v , A have fixed nonzero reals.

Lemma 2.1. Suppose that -oo(t,v,A) G C ³ [0,T], for a non-zero real v,A, where T >  0 is fixed. Then the inverse problem (2.8) - (2.11) for (z,t) G D T , D T = { (z,t) | 0 C z C t C T — z} is equivalent to the problem of finding a vector-function

[w^t^x), (^) ⁽z^,t,v,x⁾, { ^ w^ ^(z,t^,v,x^),h⁽t)^,h ^{( t ) , -} o ⁽ t ^{) , -} 0 (t), ^- , ^{( t ) , -} 0" ^{( t)}] following non-linear system of integral equations:

t

∂w

w(z,t, v, A)= в (z,v, A)+    — (z,T,v,A) dT,

z

from the

(2.14)

dw            11

-ft ^(z,t^,v,A') = — H^(v,A) + 2 (- 0 ^{( t — z,v,A) —} r o ⁽⁰⁾ g o ^{( t — z,v,A)}

t-z

1                   11

^{— h ( t — z ) z} + 7— ^k 0 ^{(t — z )} + o \ ^ko^{(t — z — r)}-0^{(r,v,A) dr}

2a,              2a,

⁺ 2

( z + t ) / 2

У   H (v,A)w(£,t + z

-

£, v, A) h(t + z — 2£) c 0

z

-

t + z- 2 ξ

У h(r)w(£, t + z — £ — T,v, A)dr^ d£. 0

z

- 2/ 0

t-z

H(v, A)w(£, t — z + £,v,A) — У h(r)w(£, t — z + £ —

=: G i [w, h,ko,k0 ],

т, v, A) dT d£

(2.15)

^d-w(z,t,v,A) = ^-G i [ w,h, ^- o , ^- 1 , ∂t ²               ∂t

(2.16)

^h(t) = ^{— 2} c 0 [go ^{( t}, ^v, ^{A ) — r} 0 ^{(0) -} 0 ^{( t, v}, ^{A )} + ^r 01 ^- 0 ^{( t, v}, ^{A ) —} 2 ^{H (v}, ^{A ) в} Q>^v, У

—2-(t) — 2c , J ЪЩ - r ) - o (r, v, A) dr — a, j h(r )в 7 t 00

-

τ

, ν, λ dτ

t

+ ² c o / H^(v,A) ~dt ^(£,^

t- 2 ξ

— ^£,v, ^a) — у ^h(r ) -ft ^{( £,t} — ^£ — 0

r,v,A)dr d£

(2.17)

=: G 2 д^Л^ ,

----

	h'(t)_ (G 2 dd^,h,M ) ,                         (2.18) t k o (t) _ — r o (O) + r oi t +    (t — t )k0(r ) dT,                       (2.19) 0 t ko(t) _ roi + 1 ко(т ) dT,                                (2.20) 0 t k'o(t) _ —h(t) + rooko(t) — ^ h( — т)ко(т ) dT.                   (2.21) 0 t k'o(t) _ —h'(t) + rook'o(t) — h(O)ko(t) — У h'(t — т)ко(т ) dT,            (2.22)
where	0 roo _    / — r0 (0),   r oi _ ('   — r (0).

⊳ Note that the following are valid:

d²w - d2w _ d(- - d \ (d_      _ dL AW— -

∂t ²    ∂z ²      ∂t ∂z ∂t ∂z ^w ∂t ∂z ∂t ∂z ^w.

Taking this into account, integrate (2.8) along the corresponding characteristics of differential operators of the first order for (z, t) G D t . Integrate along the characteristic of the operator ddt — dZ from (z,t) to ((z +1)/2, (z +1)/2) in the plane of variables ((, t ) . Using the equality ( dt + dZ ) w((z + t)/2, (z + t)/2, v, A) _ 2 C 0 H(v, A) , resulting from (2.9) after differentiation with respect to z , we have

(^{+      w(z, t, v, A )} = F ^{H ( v, A )}

\ dt dz)               2c ₀

( z + t ) / 2

+ У HH(v, A)w(£, t + z — £,v, A)--h(t + z — 2£)

(2.23)

z t+z-2ξ

— У h(T)w(£,t + z — £ — t, v, A)dT d£.

Integrate along the characteristic of dt + dZ from (0, t — z) to (z,t) . Using (2.10), (2.11), we get

∂∂ i dt - dz) w^ t,v, A) _ go(t -z, v, A) - ro(o)go(t - z, v, A)

z

t - z

1,.       1n.

--h(t — z)z +--k0(t — z) +    k0(t — z — t)qo(t,v,A) dT c0              c0

t - z

(2.24)

H(v, A)w(£, t — z + £,v,A) — У h(T)w(£, t — z + £ —

t, v, A) dT d£.

From (2.23) and (2.24) we can easily obtain (2.15). Putting z = 0 in (2.23), and using (2.10), (2.11), we obtain

t

^— 0 ^{( t}, ^v, ^{A ) -}

t/ 2

= ЛH ^(v,A)+[ H^{(v,A)w(£,t -} €^{,v,A )} 2 c 0

r0(0)g0(t, v, A) +--k0(t) + I k0(t - т)g0 (t,v,A) dT c0

t - 2 ξ

^h(t ^- 2() ^- [ h^(T)W^t ^- £ ^- c 0

т, v ) dT d£.

Differentiate this equality by t and arrive at (2.17) after simple computations.

The remaining equations of the system are obvious and are used to close the system

of integral equations. The h(0) , k " (0) are knowns if we solve for t = 0 a system equations (2.21) and (2.17). The Lemma 2.1 is proven. >

Theorem 2.1. Suppose that the conditions of Lemma 2.1 hold. Then there is a solution k 0 (t) G C ³ [0,T] to (1.7) - (1.10) for every fixed T >  0.

Let Г(К 0 ) be the set of functions k 0 (t) G C ³ [0, T], satisfying ^ k 0 (t) h c 3 [0 ,T ] ^ t G [0, T] with a positive constant K0.

of two

unique

K 0 for

Theorem 2.2. Let k001 (t),k02(t) G Г(К о ) be solutions to (1.7) - (1.10) with the set of data I g 0O) (t, v, A)} for j = 1,2 respectively. Then there exists a positive constant C = C(K0,h0(v,A),O0,T ) , h 0 (v, A) = max | ^00) (t, v, A) |^| C 3 [ ₀ , _T ] , j = 1,2}, such that the stability estimate holds:

(1) k ₀

^L^T] ^C CH )

g ⁰⁰ L³[0 ,T ]

.

(2.25)

<1 Proof Of Theorem 2.1. The main idea of the proof consists in application of the Contraction Mapping Principle to the non-linear system of the integral Volterra equations of the second kind (2.14)–(2.22). Write the system of equations as an operator equation

V = AV,

(2.26)

with v = [V j ], j = 1, 2,..., 9 :

^i(z,t, v, А) := w(z,t,v,A), ijw                1

V2^(z, t, ^v, ^{A ) :} = —⁽z, t, ^v, ^{A )} + —h ^{( t - z )} z dt              2c o

1       ,

5— k o ^{(t - z)}, 2 c o

^ 3 ⁽ z, t,^v, ^{A ) :} = ^w ⁽ z, t,^v, А) + 1— h^{,(t - z )} z dt²               2c ₀

^—о (t 2c 0 (0) ^0k

z

z)+2 h^{(t -} z) у ж^ ) de, 0

-—

.-

_w(t) := h(t)+2k0(t), ^(t) := h'(t) + 2k0 ' (t) + coh(t)e(O,v ),

✓ X

^ 6 (t) := ko(t),   W(t) := k 0 (t),   V8(t) ^: = k'0(t) + h(t) - rooko(t),

.-

-

.-

.-

—

——

——

W(t) := k0(t) + h ‘ (t) - rookO(t) + h(O)k o (t).

The operator A is determined on the set of vector-functions v G C [ D t ] and, by (2.14)(2.22), has the form A = (A i , A 2 ,..., A 9 ) :

t

A 1 ^ = ^ 01 +

-j V2(z,T,v,A)

- Д z (2^ 8 (t - z) - V 4 ( t - z) + 2r 00 V 6 (T - z)) + x^ V 7 (t - z) dT, 2 c 0                                                     2 c 0

z

A 2 ^ = ^ 02 + 2

t-z                                      z

J ^(t - z — т)go(r, v,A)dr + | J HH(v,A)^i(£,t - z + £,v,A)

t-z

У (2Ыг) — w(r)+2r oo ^ 6 (r )>1 (£,t - z + £ - r,v)dr d£ 0

t+z 2

+ 7 [ [^{H ( v}, ^{A )} ^ 1 ^(£,t ⁺ z ^{— £,v} )( ² ^ 8 ^{(t +} z ^{— 2 £ ) —} ^ 4 ^{( t +} z ^{— 2 £ ) + 2 r} 00 ^ 6 ^{(t +} z ^{— 2 £ ))}

2 J L                                  co

z t+z-2ξ

-

У (2^ 8 (r ) - w(r) + 2r oo ^ б (т))^ 1 (£,t + z

- £ - r,v, A)dr

dξ,

t-z

A 3 ^ = W3 + 2 У (w(t - z - r ) - ^ 8 (t - z - r ) - r oo ^ 6 (t - z - r))go(r, v, A) dr 0

z

⁺2 У У^{( v},^{A )} dt^ ^(£,t ^- z ^{+ £},^v )

t-z

∂w

• ^- J ⁽² ^ 8 ^{( r}) ^- W^(r) ^{+2 r} 00 ^ 6 ^{( r}))— ^{( £,t - z + £,v ) dr d£}

t+z

⁺ 7 / ^H(v,A)~^T^{(£,t -} z ^{+ £}, ^v, ^{A )}      h'^{(t +} z ^{- 2 £ )}

2 J            dt                       co

z

^{- (2}^8^{(t + z - 2 £ ) -} ^4^{(t + z - 2 £ ) + 2 r} 00 ^ 6 ^{( t +} z ^{- 2£))в(£, v} )

t + z- 2 ξ

∂w

- J (2Ыт) - W(r) + 2roo^6(r))^(£,t + У - £ - r, v, A)dr d£,

t

A 4 ^ = ^ 04 - 2c o У ko(t - r)go (r, v ) dr

t

- c o У (2^ 8 (r) - ^( r) + 2r oo ^ 6 (r)) e t У 0

-

t/ 2

τ                     ∂w

- ^,v,X) d^{r + 2} c o J H ^{( v,A)} — ^{(£,t - £,v,A)}

t- 2 ξ

∂w

^{-     (2} ^ 8 ^{( r}) ^- W^{(r )+2 r} 00 Ы^т )) d£ ^{(£,t - £ -}

r,v,A)dr d£,

A5^ = ^ o5

- c 0

t

У ⁽ ^ 4 ^{( t - r} )

- ^ 8 (t - r ) - r oo ^ 6 (t - r )) go (r, v, A) dr

t

^-"2 ° / ⁽² ^ 8 ^{( r} )

-

^ 4 (r) +2r oo ^ 6 (r)в У

-

τ

, ν,

λ

dτ

t/ 2

∂ ² w

⁺ c o J H ^{( v}, ^{A )} "dt 2’ ^{( £,t - £,V}) ^{- (2} ^ 8 ^{( t - 2 £ ) -} ^ 4 ^{( t - 2 £ ))}

t- 2 ξ

∂w                                   ∂ ² w

+ ^{2 r} oo ^ 6 (t ^{- 2 £ )} “dt ^{( £}X^V) ^- J ⁽² ^ 8 ^{( т}) ^- W ^{( т ) + 2} r ooЫ^т )) dtp ^{( £,t -} £ ^{- T,V ) dт d£}’ 0

t

A 6 ^ = W6 + y( t - T) (^(t - т) - ^ 8 (t - т) - r oo ^ 6 (t - т)) dT, 0

t

A ? ^ = ^ o7 + У (w(t - т) - ^ 8 (t - т) - r oo ^ 6 (t - т)) dт, 0

t

A 8 7 = W8 - У (2Ыт) - Ыт) + 2r oo ^ 6 (т)) ^ б (т) dт, 0

t

A " / = ^ o9 - У h ‘ (t - т)^ б (т) dT, 0

with ^ o = [<^ oi , <№, • • •, ^ oo ] :

Wi^{( z}, ^v, ^{A ) :} = ^{e ( z}’^v, ^{A )} ,

^ o2 ^{( z,t},^V,^{A ) :} = ¹ (^g o ^{( t - z,V,A ) -} r o ^{(0) g} o ^{( t -} z,^{V,A )}) +-p H ^{( v,A )} ’ ²                                            4c o

W3 ^{( z,t}’^v’^{A ) :} = 2 (^go^{( t -} y^{,V,A) -} r o ^(0)g o ^{( t -} y,^v’^{A )}) + | ^^{( v}’^{A ) в} У z+t’^v,^A ) ^- c o ^{h (0)}j ’

^ 04 (t, V, A) := - 2c o g^t, v, A)

^{- r} o ^(0)g o ^{( t}’^v’^{A )} + r oi g o ^{( t},^v’^{A ) -} 2H

(v,A) в (|,v,a) ,

^ 05 ^{( t}, ^v, ^{A ) :} = ^04^(t,^V,A)

^ 06 (t) := - r(0) + r oi t, ^ 07 (t) := r oi , ^( t) := 0, ^( t) := 0.

In (2.26) we have

h(t) = 2^(t) - ^(t) + 2r oo ^ ₆ (t),    h'(t) = 2^ 9 (t) + 2r oo^ (t) - ^(t)

+c o ⁽² ^ 8 ^{( t ) -} W^{(t ))} + ^{2 ( r} oo c o ^{e (0 , v}) ^{- h (0))} ^ 6 ^{( t})> ko (t) = ^(t) - ^(t) - r oo ^ 6 (t),

(2.27)

∂w dft(z,t,V,A) = ^2(z,t, v, A)

-

z

7— ⁽² ^8 ^{( t - z ) -} W^{( t - z )} 2c o

+2r oo ^ 6 (t - z)) + -1- ^ ? (t - z), 2c o

_∂ 2 _w

—T ^{( z}, t,^v,^{A )} = ^ 3 ^{( z}, t, ^v, ^{A )}

-

z z-titt - z) + -1-go‘(t - z) - 1h(t - z) / e(€,v,A) d€, 2co             2co o           2

ko (t) = ^ 9 (t) - h (t) - r oo ^ 7 (t) + h(0> 6 (t).

In the last two equalities, instead of h(t) , h'(t) , к'0О on the right-hand side, we take their expressions via the components of ϕ (2.26).

Introduce the Banach space of continuous functions Cσ , generated by the family of weighted norms suP \^j№ at \ , te[0,T ]

j = 4,..., 9^ , a >  0.

IMIa = max < sup \ ^ i (z,t,v,A)e ^a | ,i = 1, 2, 3, [ ( z,t ) e D T

For a = 0, this space is the space of continuous functions with the usual norm | ^ | . By the inequality

■ ' IMI C IMIa C lid (2.28)

the norms ||^| _ff and ||^| are equivalent for every fixed T G (0, to ). The positive real a will be chosen later. Let Q _a (^ 0 , ho | ) = ^: { ^ | ||^ — ^ o | _a C ho |} be the ball of radius | ^ o | with center at ^ 0 from some weighted space C _a (a ^ 0). For ^ G Q _a (^ 0 , llwll) , the following estimate holds: ||^|a C ||wIla + 11^ 0 II C 2|^ 0 Il-

Let ^(z, t, v, A) G Q _a (^ 0 , ||^ 0 II)- Next, we will show that for an appropriate choice of a >  0 the operator A takes Q _σ into Q _σ . Give, as an example, the estimating technique for the second nonlinear equation of (2.26); the estimates are obtained similarly for other equations [18]. For (z,t) G D t , we have

IIA 2 ^ — ^ 02 ||a = sup \(A 2 ^ - ^ 02 )e ^at \ ( z,t~ ) e D T

= sup ( z,t ) e D T

z

+2/

2 У ^ ₇ (t - z - T )90 (T, v, A)e -^{a ( t}-z-^T ) e ^{- a ( z + T} ) dT 0

H (v, A)^1«, t - z + £,v, A)e -^{a ( t}-z +^ e ^{- a ( z - ( )}

У (2Ыт) - w(t ) + 2Г 00Ы Т ))e^ ^aT ^ 1« , t - z + £ - T,v, A)e ^{- a ( t - z + ( - T} ^-^dT 0

dξ

t + z

+| I HH (v,A)^ i (£,t + z - £,v,A)e ^{- a ( t + z - ( )} e ^{- a ( ( - z )}

z

-a(2^ ₈ (t + z - 2£) - ^(t + z - 2£) + 2r 00 ^(t + z - 2£))e ^{- a ( t + z -2 ( )} e ^{- a (2 ( - z )}

t + z- 2 (

J (2^ 8 (t ) - ^ 4 (t ) + 2r 00 ^ 6 (t ))e ^{- aT} ^ i (£, t + z - £ - T,v, A)e ^{- a ( t + z - ( - T} ) e ^{- a ( ( - z )} dT d£ 0

C ¹ G|Ul a ¹ ( e ^{- az} - e ^{- at} )

2a

+ 2 H0|b|| a a ( 1 - e ^{- a}z ) +2 (2|Ь ||a + ||Ыа + 2r 00 | ^ 4 | a >1 l a | ( 1 - ■ ' ) T

+ 9^H0 ^H ^ 1 Ila— f ^{1 - e a 2} ^ ⁺ A--(^l^ll a ⁺ ||^ 3 ||a ^{+ 2 r} 00 11^ 4 ||a )“( ^{e a}z ^{- e a}t )

2          a \            J   2c ₀                                  ⁷ a              ⁷

+ 2 (2|b la + Iblla +2r«)Ma ) |b||a| ( 1 - e ^-^ ) T

^ ²IIWII [2G + H o + ( 3 + ^{2 | r} 00 1) ^2 c 0 ⁺ T '^⁰ ^)] a ^: = 2 ^{I w} o H ^{X 2} ( ^c o >G’H o , r oo , T, II W o II) — , H o ^: = maX z _{e [} o ,T/ 2] | H ^{( v,}A ^{) |} , G := max t _{e [} o ,T ] | g o (t,^v,A) | .

Thus, for all equations of (2.26), we have

^{| A} j W - W o j Ila < ²h w o ||X j — , ^j = 1, ² , - - -, 9

( X j are the constants depending on the same values as X 2 ).

Choosing — p — o := 2max i ^ j ^ g { x j } , we find, that A takes the ball Q _a (w o , llwoll) into Qa ⁽W o , 1Ы1) .

Let ^ 1 , w 2 be two arbitrary elements from Q _a (w o , llw o II)- Using the auxiliary inequalities of the form

|wiwi - w2w2|   ' < HI k) - j e-at + I j |wi - w2| e-at < 4|lwoI к - HL , we have ||AW - Aw2| ^ 00° I|w1 — W21| , where —oo is determined the same way as —o (the only difference between —oo and —o is that the constant ||woII in the coefficients Xj is doubled [18]).

If — is chosen from the condition — > — * := max { — o ,— oo } , then the operator A is contracting on Q _a( w o , II W o II) - Then, by the Banach Contraction Mapping Principle, equation (2.26) has a unique solution in Q _a (w o , llwoll) for any fixed T >  0-

Since ko(t) := exp(ro(0)t/2)ko(t), by the obtained ko(t) the function ko(t) is found by the formula ko(t) = exp [ — ro(0)t/2]fco(t)-                               (2.29)

Theorem 2.1 is proven. >

• <1 Proof Of Theorem 2.2. Since the conditions of Theorem 2.1 are valid, a solution to (2.26) belongs to Q a (w o , I w o I ) and ^ W iIla <  2|| w o I i = 1, 2,... , 9. Thus,

• 3. The Problem of Determining а1(хз), k1(t) and u1(x,t)

max |ko(t)| ^ 2IwoI exp (|ro(0)|T) =: Ko- te[o,T ]

Let w ^{( j )} , j = 1, 2 be the vector-functions that solve (2.26) with the set of data { g j o (t, v, A) } respectively. From the arguments in the proof of Theorem 2.1, we obtain the estimate for — >  — *

∗ p —    , < C —                — ?1,,       (2-30)

where C i depends on the same arguments as C in Theorem 2.2. The estimate

IP—l21.    H>—PU,, follows from (2.28) and (2.30). Then, considering equation (2.29) for {ko1), L2)}, {ko1), ^2)} and using (2.29), we obtain (2.25).

Next we will use the bilinear integral operator

t

L [k o (t),u(x,t)]

= u(x,t) + У

o

k o (t — т)u(x, т) dT-

Pass from the functions u i (x,t) and u o (x,t) to the Fourier images U j (x3,t,v, A) := F _x 1 ,_x 2 [u j ](x 3 ,t, v, A), j = 0,1. Then inverse problem (1.11)—(1.14) can be rewritten in terms of U i as follows:

d ² u 1 ∂t ²

- т 17    ^d 2 “ i

^L |_^k 0 , ^a 0 dx 2

-

(v ² + A 2 )a o Ui]

+L ko

dx '■

duo x ∂x 3

^ - iAa i (x 3 )u o - i ( A ² + v2)ai(x _?J )uo x

(3.1)

t

+i J aoki(t - т )

d²uo v ∂x ² ₃

-

(2vU o + ( A ² + v ² ) u o v) (х з , t, v, A) dT,

_T        n m ^дй0 * ,   ^d“ 1’

L ko ,ia i (+0)—--+ ao-—

∂x 3      ∂x 3

-

ui |t

(3.2)

Ui(0,t, v, A) = Fxi,x2 [Ui](t, v, A) := gi(t,v,A), t> 0

= 0, x3=+0

(3.3)

(in (3.1) and (3.3) the subscript v (X) denotes differentiation with respect to v (A)).

(3.4)

Let

V(z,t, v, A) = L[ko,й1(ф ⁱ(z),t, v, A)] exp (ro(0)t/2).

Then (3.1)-(3.4) take the following forms for z > 0, t E R :

∂²V

∂t²

t

∂²V

= -—77 + H(v, A)V - \ h(t - т)V(z,т, v, A)dт - iAc_i(z)w ∂z²

-i λ²

+i exp(ro(0)t/2) J ki(t - т)

+ v2) ci(z)wx +    (z)dw^ + “^ci(z)^wr c20 1 ∂z    c20       ∂z2

t

dvv - (A²+v 2 Vv -

2vc2v(z, т, v) dT,

where

(3.5)

iai(+0)

V |t<o= 0,

t

^w^ + yr + i exp(ro(0)t/2) / ki(t - т)^v^ dr]

∂z ∂z                          ∂z

V |z=+o= L kko,9((t, v, A)] ,

ci(z) := ai(coz),

ki(t, v, A) = gi(t, v, A) exp(ro(0)t/2).

By (2.1) and (2.7)

v = exp(ko(0)t/2)

= 0, z=+0

• (3.6)

• (3.7)

• (3.8)

—5(t - z) + w(z, t, v, A)^(t - z) c0

t

+ yro(t - т)exp(ko(0)т/2) ^5(7 - z) + W(z,т,v,A)6(т - z)j dт 0⁰

(henceforth we omit the tilde over w),

t

Vv = exp(ko(O)t/2) [wv(z, t, v, A)0(t - z)] + J ro(t - т)w„(z, т, v, A) exp(ko(O)т/2) dT.

z

Note that the initial-boundary value problem obtained by differentiation of (2.8)–(2.11) with respect to ν is valid for w_ν :

∂²wν   ∂²wν

∂t²     ∂z²

t

+ H(v, A)w^ + Hv(v, A)w - ^[h(t - т)w„(z,т, v, A)] dт,

z

Wv lt=z+0 = в» (z, v, A),

(3.9)

(3.10)

∂wν ∂z

= O, z=+0

(3.11)

Wv |z=+o = L [^ko ,gov (t, v, A)] .

Summarizing the above, we have

(3.12)

exp(r„(O)t/2) [ ki(t - т)dz *

= J ^ki (t - т)[ dw^V(z,т,v,A)+ J    - n)

dWzv (^n^^d^ dT,

(3.13)

where ki(t) := ki (t) exp(ro (O)t/2), ko(t) := ro(t) exp(ro(O)t/2),

t

∂2v exp(ro(O)t/2)   ki(t - т)-х-т dт

∂z²

t

= I ki (t - т)

z

∂²wν ∂z²

τ

∂²w_ν

+ / ^го^{(т -}П)“d^^(z,n^,v,A)dn^dт,

z

(3.14)

t exp (ro(O)t/2) У ki(t - т) (q(z) - (A2 + v2)c2)vv dт

= J k-^t^{- т}) (q^{(z) -}(^A2 + ^v2)c2) wv^(z,^т, ^v,^A)

z

+ У ко(т - n)wv(z,n, v, A)dn dт,

(3.15)

z

t exp(ro(O)t/2) J k1(t — т)2vc0v(z, t, v, A) dT

t

= 2vc0 k1 (t — z) + У k1(t — т)ro(t — z)dr

z

+ У ^k1 (t — т) ^w(z,T,v,A) + У ко(т — n)w(z, П, v, X)dn^ dr^. (3.16)

Observing (3.11) and (3.13)-(3.16), we can rewrite (3.5)-(3.8) for z > 0, t G R as follows:

t

• ∂²V   ∂²V

• -7-7 =     + H(v, A)V — I h(t — т)V(z,r, v, A)dr + vcki(t — z)

∂t     ∂z²

z

—iAc₁(z) ^—5(t — z) + wd(t — z)^ — i(A⁰+ v⁰)c1(z)w^

t i     ∂wλ   i     ∂2wλ

+coCi(z)~q^⁺coci(z)~q~2~ + / P(z,T,v,A)ki(t — т) dr,

z

(3.17)

where

c = 2ico,

V |t<o= 0,

dV I dz lz=+o

= 0,

V It=z = 0,

V |z=o= L [^ko,jki(t,v,A)j ,

• (3.18)

• (3.19)

• (3.20)

• (3.21)

p(z, t, v, A) = cro(t — z) — iLo

[ko’ JwV — (A⁰+ v^ww— — 2vcow

(the difference between Lo in the definition of p(z, t, v, A) and L is that the subscript of the integral in the operator is changed for z).

Thus, the inverse problem of determining а1(хз), ki(t) from (1.13)-(1.16) reduces to the problem of determining ci(z), ki(t) from (3.17)-(3.21).

By means of the d’Alembert formula, we obtain

V(z,t,v,A) = 2 (l [^kO’ki(t — z,v,A)j + L [^ko,ki(t + z,v,

-

t + z

[ ci(№ + ¹

2co               2

t-z

z t+z-ξ

/ / I ^vck1^{(T —} ^^{) + H(v,A}')V⁽^’^T,v,A)

0 t-z+ξ

^—ci⁽£)N +^T,^v,^A)+ -^wr⁽^’^T’^v’^{A) c}0 ^∂z

(3.22)

-

τ

У [h(r — n)V(^,n,v,A) + ξ

^ki(t — n)p(^,n,v,A)jdn^ dr di := F \v,ci,,ci₁ ,^ki] ,

where

N(e, T, v, A) := i [a-w + (A²+ v²)w- -

i ∂²wλ c²₀∂z²

Passing to the limit in (3.22) as t ^ z + 0 with V|_t=z = 0, we derive

z

L [^0₁§'i(2z₁v,A)] = -C0 У ci(()de

-

z 2z-ξ

+ У I y^-T^{- e) +}H^(v,A)V^(e,T,^{v,A) -}ci^(e)N(e,T,^{v,A) +}C2ci^(e)^w^-    (3.23)

0ξ                                                                               ⁰

^-J [^{h(T -}n^)V(e,n^{,v,A) +}Ы^{т -}n⁾p^(e,n, ^v, ^A)]dnj d^Td^e.

From (3.23) it follows that gi(0, v, A) = 0. Replacing 2z by t and differentiating (3.23) with respect to t, we get t/2

-L

,A)] = -^С1(ф)+ I v»i(t - 2^) + H(v,A)V((,t - e,v,A) 2c0

-ci«)n «, t - e, v, a) + 4ci(e)     «, t - e, v, a)

(3.24)

c20      ∂z t-2ξ

^-J [^{h(T)V(e,t - e -}n^{,v,A) +}Ы^т)P^{(e,t - e - T},^v,^A)]d^Tp^e-

It’s obviously that ci(0) = 2—g^(0,v, A). Differentiating (3.24) with respect to t, then substituting the values λ1, λ2 sequentially and making up the difference of the equalities for a fixed v, we can obtain the equation for c1(z)(z = t/2) :

^A(z) ann^ILM-^(2z,v,A)] I^-M^(z)     I ^{L                  J} J

2А-{N(z,z,v, A)}

M (z)

4 >z

Na (z,v,A)

- ci^(z)

✓

z

1                   .dV _      .    ,,

⁺Mz) J ^Aa H^(v,A)~dt^{(e,t- e,v,A)}

-

ci^(e)-NN^{(e,t- e,v},^A)

(3.25)

+4^) CF (^T,v,A) c²₀      ∂t∂z

2z-2ξ

^- / [^h(T)iV^(e,^{2z - e - T,v,A)+}^i(^T)dp^(e,^{2z - e - T}, ^v, ^A)] d^T | d^e, 0

where А-{-} is the difference of the values {•} for A = Ai and A = A2. In particular, A-{N(z, z, v, A)} := N(z, z, v, Ai)-N(z, z, v, A2). Next, by A_v{•} we will denote the difference of values for ν1 , ν2.

Note that if Ai = Л2, then we have

M(z) := i(Ai - Л2)

1 + 7—

4co

= 0.

Differentiating equation (3.24) by t (after replacing the variable in the first integral t — 2£ = т), and then using the parameters vi,V2 (vi = V2), we can obtain the equation for k1(t) (t/2 = z):

---- ki(t) =

c(vi — V2)

Av

{L X-g'v^(t,v,A)] }

A„ {2N (z,z,v,A)}

⁺     C(vi — V2)     c^1(z)

4            s/            Z

N(z,v,X)

—

c(vi — V2)

j Av [h(v,A)dV(€,t — e,v,A) 0

—ci ш ^dN (^ t—^^v, ^a)+2 ci^)^dw^ (^ т^v, ^a) ∂t                 c₀     ∂t∂z

(3.26)

—

t-2ξ

/ [^h(T’7^K’t-■

^{— т},^v,^A)+ Ы^т) Ip (^t^—€ ^{— T,v},^A)]d^T ? d€.

Next, the obvious equalities are used:

z

Ci (z) = Ci

(0)+/

ci^(€)de,

(3.27)

^dV^(z,t,v,A)= ^F [^V,ci^,cl^,ki] . ⁽3.²⁸⁾ ∂t ∂t

Equations (3.22), (3.25)–(3.28) are equivalent to equalities (3.17)–(3.20) and form a closed linear system of Volterra integral equations of the second kind in the domain DT with respect to V ⁽z,^t,v,^A), dV^(z,t,v,A), ci^(z), ci(z).

Next, we need that the functions N(z, t, v, A), p(z, t, v, A) G C ¹[Dt]. Therefore, it must be shown that w^,w_vG C³[Dt].

Indeed, using the d’Alembert formula for the problem (3.13), (3.15), (3.16) we obtain a linear integral equation of the Voltaire type with a continuous free term and a continuous kernel in the domain DT :

wν

2 (l [^ko,gov(t — z, v)] + L X,kov(t + z,v'

⁺2

z t+z -ξ                                         τ

/ I I H (€,v)wv ⁺Hv (€,v)w(€,T,v) — У h(T — n)wv (€,n,v))dn?dTd£.

(3.29)

0 t-z+ξ                                         ξ

It follows from the theory of integral equations that equation (3.29) has a unique continuous solution in DT . The smoothness of the solution is determined by differentiating equation (3.29) a sufficient number of times. It is easily checked that the right part of the differentiated equation will be continuous, and therefore the left part will also be continuous [30]. Thus, Wv G C³[Dt].

Similarly, it can be proved that w\ E C³[Dt].

The following theorems of unique global solvability and stability of the inverse problem of determining ai (y), ki(t) are the main results of this section.

Theorem 3.1. Under the conditions of Theorem 2.1, let gi(t, v, A) E C²[0,T] for fixed non-zero (v, A), and gi(0, v, A) = 0, g1(0,v, A) = i^C^⁰. Then there is a unique solution of inverse problem (1.11)—(1.14) c₁(z) E C¹[0,T/2], k₁(t) E C[0,T] for every fixed T > 0.

Theorem 3.2. Let ci¹⁾(z),c1²⁾(z) E C ¹[0,T/2], k^¹(t), k^²(t) E C[0,T] be solutions to (1.11)—(1.14) with

{g?(t,v,A), kj(t), uj)(x3,t,v,A)} for j = 1, 2 respectively. Since the conditions of Theorem 2.2 are valid, there exists a positive number C = C(C, h1 (v, A)), hi(v,A)=max^||g(’)(t,v,A)||C2[0,Tp ||N(j)(z, t, v, A) ||C1(DT), ||p(j)(z, t, v, A)||C1(DT), j = 1, 2 j, such that the stability estimate holds:

11 ci¹) - ^c1²⁾|^|ci [o,t/2]⁺ |^{| k(1)}- kF |^|C[0,T]

Ф C

П _й⁽¹)__й⁽²)н +H k^{)2-k^{1

II^g1 ^g1 IIc²[0,t]⁺l^k0      ^k0 llc[0,T]

(3.31)

<1 Proof Of Theorem 3.1. System (3.22), (3.25)-(3.28) is a closed system of the linear integral Volterra equations of the second kind with continuous free terms and kernels in DT . The idea of proving existence of the unique solution to the given system consists in application of the generalized contraction mapping principle. Write the system (3.22), (3.25)–(3.28) as the operator equation ф = Вф, (3.32)

Ф :=

t+z

t-2 z

4                   sz

ψ1

k1(2z) - N(z,v,A)c1 (z), C1(z), ''

ψ3                ψ4

^dVz          ¹    - zM  ^V7

~ai(z't'^ + TE, 4~)-~}\  ¹ k^{1 (t-z)cz}

4                                             sz                                             Z

ψ5

Then V(z,t,v, A), c1(z), k1(2z), dV(z,t,v,A) can be defined through the components of ф:

V^(z,t,v,A) = Ф1⁽^^,т,v) + 1— 2c0

τ+ξ

У ф4(s) ds,

τ-ξ 2

cl (z) = ^2(z, v, A) - N\(z, V, A)^4(z), ki(2z) = ^(z, v, A) + Nv(z, v, A)^4(z), dV                        1       + z} t-- ar (z, t,v,A) = -Uz, t. V,A) -    ^4        - ^4 —J

- V2 [^3 ((t - z)/2, V, A) + Nv(z/2, v, A)^4(z/2)] cz.

The operator B = (Bi, B2, B3, B4, B5) is determined on the / G C(Dt) for fixed v, A. Similarly, as it was done in [31], it can be shown that some degree of n (n is natural number) of the linear map Bψ is compression. Let

Ml =max max |/⁽z,t,^v,X)\, j = 1,..., 5 к [ (z,t)eDT                                   J

Let ^⁽ⁱ⁾, ^⁽²⁾be continuous vector-functions in Dt satisfying a linear system of integral equations (3.32). Let

△(z, t) = {(£, т): 0 < £ < z, t - z + £ < т< t + z - £} ,

S(z,t,£)= {т : (£,т) G△(z,t)} .

Then, by virtue of the linearity of (3.32) for (z,t) G Dt according to the equations (3.22), (3.25)–(3.28) we have (the parameters ν, λ will be omitted from the argument list)

BjA1 - BjA2 I (z, t) £ ^jz lk(1) - A2 II , j = 1,... 5, where µj are constants depending on the parameters of C (Theorem 3.2). If M := max{^1, ^2, ^3, ^4, ^5}, then we have

⁽z, t) ^Gdt.

max^ |Bj/⁽¹⁾- Bj/⁽²⁾| (z, t) < Mz |p⁽¹⁾- A²

Next, the following estimate are hold [31]

max ^M1) - B.A2 1 (z, t, v) £ M2 z- L(1) - A2 H ,  (z, t) G

1 - BnA2 | (z, t, v) ^ Mnz- L(1) - ^(2) || ,   (z, t) G Dt,

1^j^5 I j                j I                          n! IIII

( T\n

|bnA¹ - BⁿA² | < MⁿIp¹) - /⁽²⁾| .

For every fixed T we can choose the number n so large that

Tn

Mn 2.

n!

=: a < 1.

Then Bⁿ is a contraction. By the generalization of the Contraction Mapping Principles the equation B/ = / has one and only one solution belonging to C(Dt). This solution can be found by successive approximations. >

<1 Proof Of Theorem 3.2. Let ^(j be a vector of functions which are solutions to (3.32) with {gj\t\ k^j(t), w^(j^(z,t)}, j = 1, 2, respectively.

Obviously, the function 1/M(z) can be estimated:

M (z)

^|A1 ^-A2|

Further, from the arguments of Theorem 3.1, we obtain

^⁽¹⁾— ^⁽²⁾II < ^₀Y + a IM¹) — И2’

(3.33)

where

-

gi²⁾I

¹   llc²[0,T ]

+H¹’

-

k(²’ I

⁰IIC [0,T ]

and ^o depends on the parameters of C. It follows from equality (3.33) that

|^(1’ — ^(2’ | < ^y with ц = до/(1 — a).

Considering the equation k₁(t) = exp[ko(O)t/2]k₁(t) for {k⁽¹’,fc⁽¹’}, {ki²’,^i²’} and using (3.33), we obtain (3.31). Theorem 3.2 is proven. >