Аналитическая модель компенсации двигательной ошибки в адаптивном управлении движением биомеханической системы

В работе А.П. Батенко [2] предложен достаточно простой, но эффективный метод синтеза управления с обратной связью. В этой связи мы выдвинули гипотезу о возможности использования предлагаемого метода в синтезе адаптивного управления в движениях биосистем.

За одну из возможных форм адаптивного управления можно принять разомкнутое управление [2]. Задача разомкнутого управления заключается в переводе объекта управления из начального фазового состояния [So, Vo] c заданной координатой [So] и скоростью [Vo] в конечное фазовое состояние [Sk, Vk] c заданной координатой [Sk] и скоростью [Vk]. Время движения [Tk] в разомкнутом управлении не

рое обеспечивает возврат объекта движения

регламентируется.

Закон управления . Для заданных условий задачи закон управления, в котором от

на программную траекторию.

Возвращение объекта движения на программную траекторию может быть достигну-

сутствует время выполнения задачи, имеет вид [2]

и —

К² - V ² ko

2( S_k — S o ),

а движение объекта, осуществляемое по закону (1), описывается дифференциальным уравнением:

то при условии, что адаптивное управление формируется на основе обратной связи, учитывающей информацию о текущем состоянии объекта по координате и скорости [ S , V ]. Закон управления с обратной связью может быть получен заменой в (1) начальных значений фазовых координат [ S o , V o ] их текущими значениями [ S , V ]:

d 2S

2 — ( S k - S ) + dt

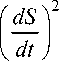
— v_k ² .

Программное управление . Решением (2)

V_k ² - V ² 2( S k - S ).

является функция

S = S o + V o t +

( к²-К² I t² ko^t .

( 2( S k - S o ) ^J 2

Элементами первой и второй производной по t от S в уравнении (3) являются скорость ( V ) и ускорение объекта ( и )

В работе [2] показано, что закон управления (6) можно привести к виду, в котором в синтезируемом управлении присутствует обратная связь по текущей координате ( S ) и текущей скорости ( V )

и — k_o + k_sS + k_vV ² . (7)

Здесь коэффициенты k o , k s , k v зависят от но-

— = V — V + Vk--Vo-1, dt o  2(Sk - So)

d ² S _— u _— V k ² - Vo²

dt ²        2( S k - S o ).

мера квадранта, в котором находится изображающая фазовая точка объекта:

^ko =

v,2-v2 ( s v2

' k o о 1 - o + ^r o

2( S k - S o ) ( A S ^J 2 A S ,

Уравнения (3, 4) суть заданного про

^kS ^—

граммного управления при наложенных условиях на начальное и конечное фазовое состояние объекта. Время движения ( T V ) не рег-

V. 2 - V 2

ko

,;

2AS(Sk - So)  V2

если квадрант I ( x >  0, y >  0);

ламентируется, но определяется из выражения

T _— 2( S k - S o ) V V_k + V_o

k_o —

.

V ² - V_o ² L S_o I V ² k o 1 o I k

2( S k - S o ) I   A S ^J 2 A S ,

Уравнения (3, 4) являются уравнениями программного управления, обеспечивающие перемещение объекта из начального фазового состояния [ S o , V o ] в конечное фазовое состояние [ S k , V k ], в соответствии с заданным законом (1) изменения ускорения ( и ).

Адаптивное управление. Задача возвращения объекта на заданную траекторию появ-

^kS ^—

V² - V ²           1

ko

,                                ;

2 A S ( S k - S o ) V 2 A S

если квадрант II ( x <  0, y >  0);

К2-К2 ( S \ V2 k — Vk----Vol 1 + SO. I-'°, o 2(Sk - So) (   AS J 2AS

К ² - V ²          1

ko ks                        , kv          ;

^S    2 A S ( S k - S o ) V 2 A S

ляется в том случае, если заданное начальное фазовое состояние объекта по координате не соответствует параметрам заданного программного управления в начальный момент времени ( t o ). Такой ситуации в технической

если квадрант III ( x <  0, y <  0);

подготовке спортсмена соответствует двигательная ошибка упражнения, возникающая в процессе выполнения целевого упражнения [4, 5, 9, 11]. В этом случае необходимо синтезировать такое адаптивное управление, кото-

, Vk ² - V o ² C, S o I V_k ² k„ — 1 + , ^o 2( S k - S o ) ( A S ^J 2 A S

V ² - v ²          1

ko ,                           ;

S    2AS(Sk - So) V 2AS если квадрант IV (x > 0,y < 0).

Номеру квадранта соответствует местоположение фазовой точки, ограниченной ося-

ми ( x , y ) прямоугольной декартовой системы координат в соответствии с уравнениями (8).

Вычислительный эксперимент. На первом этапе вычислительных экспериментов рассматривалось движение материальной точки (кисть, стопа, общий центр масс тела спортсмена) под действием программного управления (1). На втором этапе рассматривалась возможность использования адаптивного управления для компенсации двигательной ошибки и возвращения объекта движения на программную траекторию.

Программное управление. Исходные данные для программной траектории объекта движения: начальное фазовое состояние [ S o = 1,00 м, V o = -1,0 м/с], конечное фазовое состояние [ S k = 0 м, V k = 0 м/с]. Пусть A S = 0,05 м. Тогда время движения равно

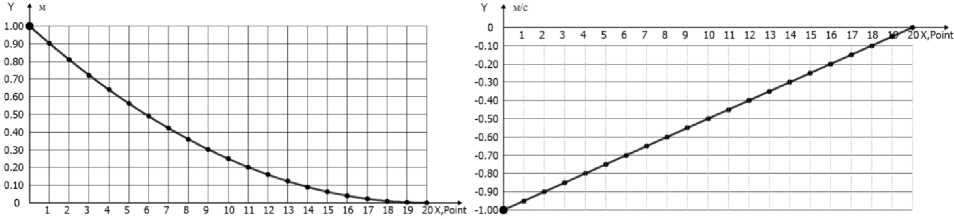
A - Координаты                               B - Скорость

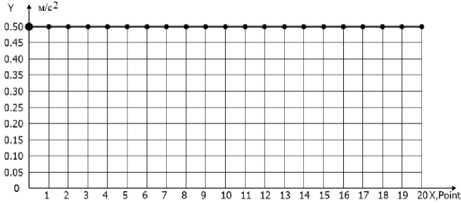
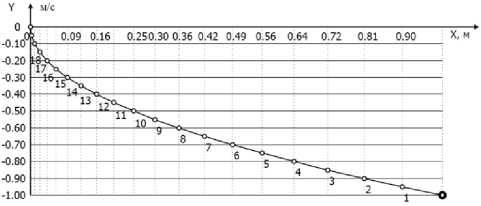
C - Ускорение                             D - Фазовая траектория

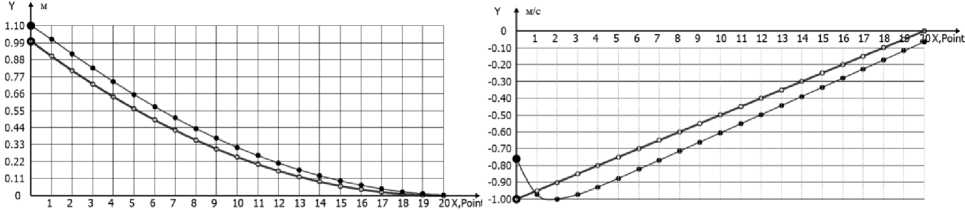
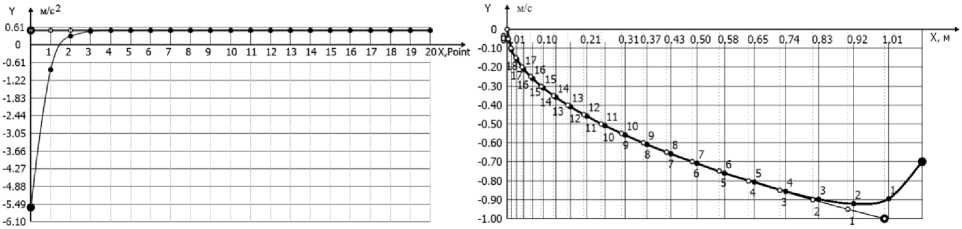
Рис. 1. Элементы программной траектории (A, B, D) и программного управления (C) Fig. 1. Program trajectory (A, B, D) and program control (C) elements

B - Скорость

A - Координаты

C - Ускорение

D - Фазовая траектория

Рис. 2. Элементы программной траектории (–o–; A, B, D) и программного управления (–o–; C), адаптивной траектории (A, B, D) и адаптивного управления (C)

Fig. 2. Program trajectory (–o–; A, B, D), program control (–o–; C), adaptive trajectory (A, B, D), and adaptive control (C) elements

2,0 с, что следует из (5). Программная траек тория и ее элементы, реализующие поставленную задачу, показаны на рис. 1.

Временная длительность движения поделена на 20 точек (рис. 1). Шаг выдачи результатов вычислений - 0,1 с, шаг интегрирования - 0,001 с. По условиям поставленной задачи коэффициенты закона управления (7) из формульных зависимостей (8) будут рассчитываться для IV квадранта. Закон управления принимает вид: и = 0,5 - 10 S + 10 V ².

Адаптивное управление . Двигательная ошибка, характеризующая отклонение объекта движения от начального состояния, задавалась списком [ S o = 1,10 м, V o = -0,70 м/с]. В соответствии с условиями задачи конечное фазовое состояние объекта задано в виде:[ S k = 0 м, V k = 0 м/с].

Координаты объекта ( S ) и скорость ( V )

вычислялись численным

интегрированием

системы уравнений:

V = и ,

_ S = V .

Результаты вычислительного эксперимента с использованием адаптивного управления, корректирующего отклонения от программной траектории, приведены на рис. 2.

Выводы

• 1.    Программное управление с постоянным ускорением реализует задачу приведения объекта из начального заданного фазового состояния в требуемое конечное фазовое состояние.

• 2.    Адаптивное управление выполняет задачу нейтрализации двигательной ошибки и приводит объект движения в конечный момент времени в заданную точку пространства.

• 3.    Полная компенсация двигательной ошибки по скорости не достигается, и в конечный момент времени достигнутая скорость не соответствует заданной.