Аналитические и численные оценки вероятности усталостного разрушения элемента трубопровода, нагруженного внутренним давлением

Развитие усталостных трещин является одним из доминирующих механизмов достижения предельных состояний конструктивных элементов трубопроводного транспорта. Циклическую прочность и ресурс конструктивных элементов трубопроводов приходится обеспечивать в условиях высокого уровня неопределенности, обусловленного [1–3]:

– разбросом начальных размеров трещин и других макродефектов, пропускаемых в эксплуатацию;

– разнообразием механических свойств конструкционных материалов;

– случайным характером процессов деградации конструкционных материалов;

– стохастической природой процессов нагружения.

В рамках детерминистических подходов учет названных неопределенностей традиционно осуществляется путем введения системы запасов по напряжениям и количеству циклов нагружения.

В настоящее время в связи с необходимостью реализации появившихся риск–ориентированных подходов к обеспечению циклической прочности и безопасности технических систем все более активно прибегают к вероятностным методам, при использовании которых неизвестные параметры математических моделей заменяются на вероятностные распределения. После этого с помощью методов теории прочностной надежности устанавливается вероятность усталостного разрушения P , которая затем сопоставляется с нормативным предельно допустимым значением вероятности разрушения [ P_F ] [4].

Учет влияния стохастических вариаций размеров дефектов, нагрузок и свойств материалов при описании процессов накопления усталостных повреждений и разрушения осуществляется в рамках вероятностной механики разрушения, развитой в классических работах отечественных и зарубежных авторов [1, 5–8].

Приложения вероятностной механики разрушения к решению практических задач отражены в работах Н.А. Махутова, С.А. Тимашева, В.В. Москвичева, А.М. Лепихина, С.В. Доронина [9–13], в которых рассматриваются вопросы статистики технологической дефектности, характеристик механических свойств и трещиностойкости конструкционных сталей, нестационарности циклического нагружения, оценки вероятности разрушения при циклическом нагружении, формулировки концепции ресурсного проектирования при стохастическом варьировании различных параметров, входящих в кинетические уравнения развития трещин.

Оценки вероятности усталостного разрушения могут быть получены путем вероятностного описания процессов роста усталостных трещин с учетом различных источников неопределенностей. В частности, в работах [14, 15] рассматриваются неопределенности, связанные со случайным характером эксплуатационного нагружения. Неопределенности, обусловленные случайным характером параметров, задающих кинетику трещин (в частности константы C и m в уравнении Пэриса), рассматриваются в работах [16–18]. В статьях [2, 19] устанавливается, как разброс начальных размеров трещин сказывается на вероятности усталостного разрушения и циклической долговечности конструктивных элементов. Работа [20] посвящена оценке влияния статистической вариативности вязкости разрушения на прочностную надежность трубопроводов и сосудов давления.

В данной статье сделана попытка выяснить, как неопределенности, касающиеся начального размера трещин, параметров уравнения Пэриса и вязкости разрушения, связаны с кинетикой трещин и вероятностью разрушения конструктивных элементов, подвергающихся циклическим нагрузкам.

Будем считать, что кинетика трещины описывается модифицированным уравнением Пэриса:

da _rKKL ) ”

^           , dN (1 - R )

с начальным условием

N = 0:    a = a0, где a — глубина протяженной поверхностной трещины, c — длина трещины (a/c ^ 0), a0 — начальная глубина трещины; C и m — постоянные, зависящие от материала и условий нагружения, N — количество циклов нагружения, R = S^/S^ — коэффициент асимметрии цикла нагружения, S и S — минимальное и максимальное значения напряжения в цикле нагружения, K — коэффициент интенсивности напряжений нормального отрыва, AK, — размах коэффициента интенсивности напряжений нормального отрыва в цикле нагружения.

В случае протяженной трещины, образующейся на внутренней поверхности элемента трубопровода с толщиной стенки t , нагруженного внутренним давлением, при a/t <  0,25 можно принять [21]:

к , = i,i . s vn a f c ,

где f — поправочная функция, отражающая кривизну поверхности трубы:

f c =

- 22— 1- + 1 - 0,5 Ja/t

t

Здесь r и r — наружный и внутренний радиусы трубы. Тогда размах коэффициента интенсивности напряжений в цикле нагружения определяется выражением A K, = 1,1 Vn a f ■ A S , где A S = S max - S min — размах напряжений в цикле нагружения.

В качестве критерия разрушения в настоящей статье используется критерий хрупкого разрушения тела с трещиной:

Ki = Kic,(5)

где K — вязкость разрушения, равная

Kc = 1,1-Smax V^a. fa ,(6)

Ic           max при этом Smm = AS/(1 R) — максимальное напряжение в цикле нагружения. Таким образом, условие разрушения может быть записано в виде:

Kic < 1,1-Smax П f c .(7)

Величина критической глубины трещины a , при которой для заданного уровня максимальных напряжений в цикле нагружения происходит разрушение, находится из выражения (6):

ac

Ic c max

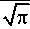
При этом условие разрушения (7) для заданного уровня максимальных напряжений в цикле S можно выразить через глубину трещины a , достигаемую после N циклов нагружения:

U n >  a c .                                                   (8)

Соответственно, вероятность усталостного разрушения после N циклов нагружения запишется как

P f = P ( U n > a c ) .                                           (9)

В наиболее общей постановке все параметры, фигурирующие в кинетическом уравнении (1) с начальным условием (2) и в критерии хрупкого разрушения (4), следует считать вероятностными. В данной статье представлены: аналитическое решение, в котором единственным параметром, полагающимся вероятностным, является начальная глубина трещины a ; численное решение, в котором в качестве вероятностных рассматриваются начальная глубина трещины a , вязкость разрушения K , а также константы кинетического уравнения C и m . Проводится сопоставление полученных решений.

В настоящее время для оценки вероятности усталостного разрушения элементов технических систем все более широкое распространение получают байесовы подходы, в рамках которых априорные оценки вероятности разрушения, основанные на исходной информации и допущениях о законах распределения случайных параметров и имеющейся статистике, уточняются с помощью данных, получаемых в ходе мониторинга состояния и технических инспекций рассматриваемых конструктивных элементов. На выходе байесовые процедуры дают уточненные апостериорные оценки вероятности разрушения [22, 23]. При этом точность результатов байесовых процедур при ограниченном объеме данных инспекций существенным образом зависит от адекватности априорных оценок, получению которых и посвящена данная статья.

• 2.    Аналитическое решение

Рассмотрим задачу циклического нагружения элемента трубопровода, содержащего трещиноподобный дефект, в случае регулярных циклов с постоянной амплитудой.

Обратимся к кинетическому уравнению (1). Кроме того, будем считать, что начальная глубина трещины a , которая фигурирует в выражении для начального условия (2) при решении задачи Коши, является случайной величиной, распределенной по экспоненциальному закону:

F ( a 0 ) = 1 - e" a ^{o/ ц} a ⁰ ,

где ц — математическое ожидание начальной глубины трещины. Остальные параметры математической модели, в том числе константы C и m в уравнении (1), вязкость разрушения K , геометрические параметры рассматриваемого конструктивного элемента, будем считать детерминированными величинами.

Для труб большого диаметра поправочная функция на кривизну f привносит, согласно выражению (4), незначительный вклад в коэффициент интенсивности напряжений (3) и, в первом приближении, может быть принята равной единице [21]. Следует отметить совпадение формулы для коэффициента интенсивности напряжений (3) в случае протяженных ( а(е ^ 0) трещин глубиной а /§ <  0,25 и f = 1 с формулой, рекомендованной Правилами и нормами в атомной энергетике (см. ПНАЭ Г-7-002-86 Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок) для цилиндрических, сферических, конических, эллиптических и плоских элементов, нагруженных внутренним давлением при отсутствии изгибающих моментов [24]. Тогда уравнение, описывающее кинетику трещины, принимает вид:

da _| 1,1 -A S Vn a = C I

dN I 1 - R

После разделения переменных в уравнении (11) и интегрирования получаем:

^da = CN (^S- 1 ( 1,1 vn a ) m      1 ^{1 -} R J

откуда вытекает выражение для глубины трещины a после N циклов нагружения:

aN

a ₀ *" m ² + NC I 1

m V 1,1 Vn

m V/^{(2- m} )

1 - R

A S о

Таким образом, из (13) следует, что между глубиной трещины после N циклов нагружения a и начальной глубиной трещины a существует детерминированная функциональная зависимость.

Критерий хрупкого разрушения тела с трещиной (5) запишем в виде:

K i = 1,1 - S max ^ = K i с .

Отсюда может быть получено выражение для критической глубины трещины a , при достижении которой произойдет разрушение элемента:

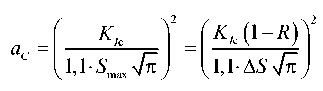
aC

При этом условие разрушения (14) для заданного уровня максимальных напряжений в цикле выражается через критическую глубину трещины:

a N >  a C

Введем понятие критической начальной глубины трещины a , под которой будем понимать такую начальную глубину трещины, которая после N циклов нагружения при заданном уровне размаха номинальных напряжений в цикле нагружения A S достигнет критического размера а_с , определяемого в соответствии с соотношением (15).

В связи с тем, что в рассматриваемой постановке кинетика роста трещины является детерминированной и между величинами a и a существует детерминированная функциональная зависимость (13), условие разрушения (16), записанное для момента разрушения через соотношение между достигнутой глубиной трещины a и критической глубиной a , также выражается через соотношение между начальной глубиной трещины a и ее критической начальной глубиной a :

a 0 >  a 0 C_N

.

Величину a можно получить, если из (13) выразить a a0

_п (2 - m М2

a

- NC

m A²/ ( 2- ^m )

и подставить в него a_N = a_c :

^a 0 С N

a ( ^{2 -} m ^{)l 2} - NC

m A²/ ( 2- ^m )

.

С учетом соотношений (9) и (17) выражение для оценки вероятности усталостного разрушения после N циклов нагружения представимо в виде:

P F = P ( a 0 >  a 0 C n ) .

Следовательно, вероятность разрушения может быть выражена через функцию распределения случайной величины F ( a ₀) — «начальной глубины трещины»:

P ( a 0 >  a 0 C„ ) = 1 ^- P ( a 0 <  a 0 C„ ) = 1 ^{- F} ( a 0 C„ ) .

Для экспоненциального распределения a при учете (15) найдем:

P F

P ( a 0 >  a 0 C_N )

(a,. )

= exp — C N - I .

l^ a0 J

Тогда, если принять во внимание выражения (18) и (19), формула для вероятности разрушения конструкционного элемента после N циклов нагружения примет вид:

P f = exp

—

^ a 0

2 - m

m

A 2/^{(2 -} m )

.

Из выражения (23) следует, что вероятность усталостного разрушения рассматриваемого элемента зависит от числа циклов нагружения N , уровня исходной дефектности, который характеризуется параметром p , размаха действующих напряжений A S , вязкости разрушения K_lc и статистического разброса этого параметра.

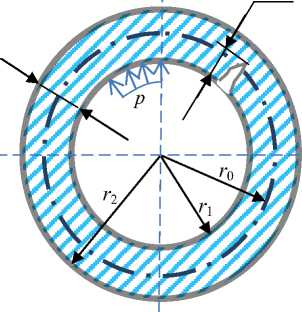
В качестве примера рассмотрим нагруженный внутренним давлением элемент трубопровода, содержащий трещиноподобный дефект на внутренней поверхности (Рис. 1). Исходные данные сведены в таблицу 1. На рисунке 2 представлены зависимости вероятности разрушения от числа циклов нагружения для трех уровней начальной дефектности, определяемых величиной математического ожидания р начальной глубины трещины a . Точка пересечения полученного графика с линией, соответствующей предельно-допустимой вероятности разрушения [ P_F ] , и есть оценка N_c циклической долговечности рассматриваемого элемента. Из сопоставления полученных зависимостей следует, что расчетная вероятность разрушения существенным образом зависит от уровня исходной дефектности.

a

δ

p

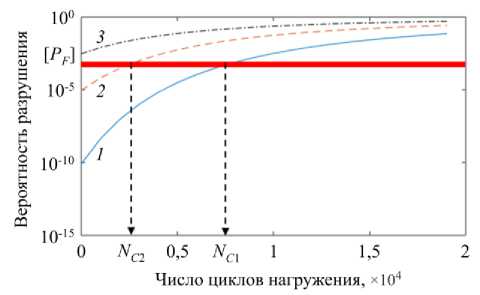
Рис. 2. Зависимости вероятности разрушения от числа циклов нагружения для трех расчетных значений ц_ао , м: 0,001 (кривая 1 ); 0,002 ( 2 ); 0,004 ( 3 )

Рис. 1. Рассматриваемый конструктивный элемент

Таблица 1. Расчетные параметры аналитического решения

Название параметра	Тип параметра (детерминированный/вероятностный)	Значение/распределение
Размах давления за цикл нагружения A p , МПа	Детерминированный	0,8
Коэффициент асимметрии цикла нагружения R	Детерминированный	0,9
Начальная глубина трещины a , м	Вероятностный	Экспоненциальное Ехр ( 1/ ( 2 - 10 - 2 ) )
Параметр C уравнения Пэриса, м/(цикл (Па·м1/2) m )	Детерминированный	3,0·10-11
Параметр m уравнения Пэриса	Детерминированный	2,9
Радиус срединной поверхности r , м	Детерминированный	0,63
Постоянная толщина стенки 5 , м	Детерминированный	0,025
Окружное напряжение а , МПа	Детерминированный	201,6
Вязкость разрушения K , МПа·м1/2	Детерминированный	61

• 3.    Численное решение

Обратимся к численной оценке вероятности разрушения рассматриваемого элемента трубопровода. В этом случае кинетические уравнения, описывающие рост усталостной трещины, могут иметь более сложный вид, а количество параметров, которые рассматриваются как вероятностные, может возрасти. При этом типы распределений параметров выбираются в соответствии с теоретическими представлениями об их характере и уровне неопределенности в задаче.

По-прежнему считаем, что кинетика поверхностной трещины в рассматриваемом элементе трубопровода описывается модифицированным уравнением Пэриса вида (1) с начальным условием (2 ) , а в качестве критерия разрушения также воспользуемся критерием хрупкого разрушения (5). Учитывая кривизну стенки трубопровода и изменение размера трещины в процессе циклического нагружения с помощью поправочной функции (4) в выражении для коэффициента интенсивности напряжений (3), кинетическое уравнение (1) запишем в виде:

da _ d 1,1 "^ ^ dN ~ I 1 - R

22          ^m

Г + Г                     t I       X™/2

—---^ +1 - 0,5 Ja/t — I (na)

r 2 - r l                  J r 2 )

Тогда выражение для критерия хрупкого разрушения тела с трещиной, с учетом кривизны цилиндрической поверхности и изменения глубины трещины в процессе циклического нагружения, будет следующим:

K i с = 1,1 - ^ max ^

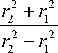
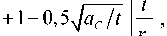
где ^ max = A 5 /(1- R ) — максимальное напряжение в цикле нагружения, K_/c — вязкость разрушения.

Условие разрушения примет вид:

К_к <  1,1 —

I с       1 - R

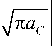
2      2

-2 ⁺ r 1

'2 — r l

+ 1 — 0,5 a_c 11

t r2

Согласно принятому критерию хрупкого разрушения критическая глубина трещины a_c численно находится как корень уравнения (25). При организации численной процедуры в качестве исходного приближения a_c к искомому значению а_с может быть задана оценка величины критической глубины трещины, получаемая без учета поправок на кривизну элемента и изменение глубины трещины в процессе циклического нагружения [2]:

. ₌ Г ^ c ( 1 — R ) '²

' C  V 1,1-ASvn.

Среди параметров, фигурирующих в кинетическом уравнении (24), начальном условии (2) и критерии разрушения (25), будем считать вероятностными величины C , m , a₀ и К _/с. Следовательно, вероятностной является также и величина a . Причем тип распределения можно выбирать в соответствии с физическими представлениями о конкретном параметре или уровне неопределенности, присущей рассматриваемой задаче.

В соответствии с избранными равномерными распределениями случайных параметров C и m, экспоненциальным (или нормальным) распределением параметра a , определяющими кинетику трещины в процессе циклического нагружения, а также распределением Вейбулла параметра К/с, с которым связана критическая глубина трещины a , генерируются случайные комбинации этих параметров :

{ a ⁽ j ) , C ^{( j} ) , m" j ) , К ⁽ _с j ) j , j = 1, 2,..., M_n . Далее для каждого из сочетаний последовательно осуществляется:

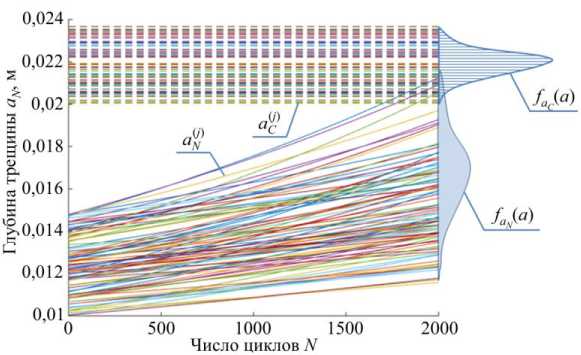
Рис. 3. Вероятностное описание роста трещин и усталостного разрушения с учетом статистического разброса значений параметров a ₀, С , m и К I c

- интегрирование уравнения (1) (решение задачи Коши) с получением кривой роста трещины Cr(j) (Рис. 3), представляющей собой зависимость глубины трещины от количества циклов нагружения a (j ) = a(j)(N), j = 1, 2, _, Mn;

- определение    путем    решения уравнения (25) величины критической глубины        трещины        a(cj), соответствующей      выборочному значению К^cj);

- проверка выполнения условия разрушения (8) в форме   a ⁽ j ') >  a⁽_с j )

(в пределах заданного числа N циклов нагружения 0 <  N <  N_e ).

При этом делается допущение, что все комбинации

параметров {a(j), C(j), m^j), К(cj)j являются равновероятными, то есть для сложного события {Cr(j) = CrH пК(сj) = Кки} , которое формулируется как «Выборочная j -я кривая Cr(j) роста трещины совпадает с истинной кривой Cr^ и выборочное значение вязкости разрушения К(Icj) равно истинному значению вязкости разрушения К/си», априорная вероятность представляется как

P Cr ⁽^ =Cr „n К ^ =К , СИ j    ¹ M n

( j = 1, 2, _ , M n ).

Считаем, что события { Cr ^{( j} ) = Cr^ п К ⁽ _с ^j ) = К _/си j , j = 1, 2,

., M_n образуют полную группу событий.

Таким образом, оценку вероятности разрушения получаем с помощью метода Монте-Карло путем многократного численного интегрирования уравнения (25) и сопоставления значения глубины трещины a ^{( j )} с соответствующим значением критической глубины трещины a (, ^j ) для различных сочетаний величин случайных параметров a , C , m и K . Поскольку в рамках априорной оценки все комбинации параметров являются равновероятными, то зависимость вероятности разрушения от числа циклов нагружения P_F ( N ) будет равна отношению количества кривых М_с из выборки j = 1,2, .., M_n, для которых выполняется условие a j > a ⁽ _с ^j ) , к общему числу кривых М_п :

PF ( N ) =

Me (N)

M n

Для численной реализации описанного решения написана файл-программа в среде Matlab, позволяющая, в частности, формировать выборки значений случайных параметров из наиболее часто используемых вероятностных распределений, в том числе экспоненциального, равномерного, нормального, логарифмически нормального, Вейбулла и других. Далее, с помощью встроенных в Matlab алгоритмов генерации случайных чисел из выбранных распределений параметров a , C , m и K реализуется процедура численного интегрирования согласно методу статистических испытаний (методу Монте-Карло).

Численное интегрирование кинетического уравнения трещины (24) с учетом корректирующей функции (4) позволяет получать уточненную оценку вероятности разрушения. На рисунке 4 в линейных и полулогарифмических координатах представлены зависимости вероятности разрушения рассмотренного в разделе 2 конструктивного элемента (Рис. 1) с параметрами, приведенными в таблице 1. Кривые получены на основе аналитического выражения (23) в предположении, что в выражении для коэффициента интенсивности напряжений f = 1, и численного решения для того же примера, использующего корректирующую функцию f в виде (4), позволяющем учесть изменение глубины трещины в процессе циклического нагружения и кривизну поверхности элемента трубопровода. При этом единственным вероятностным параметром полагалась начальная глубина трещины, которая считалась распределенной по экспоненциальному закону с математическим ожиданием р = 1 - 10 " ³ м. Из сопоставления полученных графиков следует, что оценки, получаемые аналитически и численно, весьма близки, при этом аналитическое решение, основанное на упрощающих допущениях (см. раздел 2), дает неконсервативные оценки вероятности разрушения.

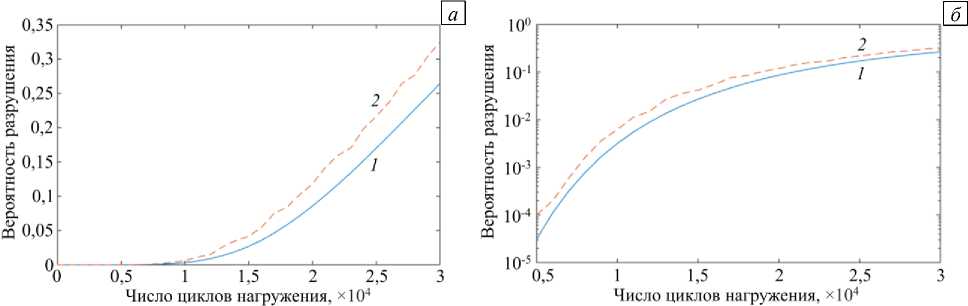
Рис. 4. Зависимости вероятности разрушения от числа циклов нагружения в линейных ( а ) и полулогарифмических ( б ) координатах; 1 – аналитическое решение, 2 – численное решение

Рассмотрим тот же пример расчета вероятности разрушения элемента трубопровода, нагруженного внутренним давлением и содержащего осевую поверхностную трещину на внутренней стенке, что и ранее (см. Рис. 1). Но теперь будем считать, что не только начальная глубина трещины a , но и параметры C , m и K являются вероятностными. При этом тип распределения может быть выбран в соответствии с физическими представлениями о конкретном параметре или уровне неопределенности в рассматриваемой задаче. В данном примере параметры С и m кинетического уравнения полагаются распределенными по закону равномерной плотности, начальная глубина трещины a — по экспоненциальному или нормальному закону, а вязкость разрушения K — по закону Вейбулла:

C ~ U ( a C ; p c ) , m ~ U ( a m ; p m ) ,     a o ~ N ( ц a ₀; ^a a ₀ )

или

a 0 ~ Exp ( 1 ц _{а о}) ,     K i c ~ W ( a к ; P к ) .                               (30)

Здесь: a_c и P_c (или a_m и P_m ) — соответственно левая и правая границы интервала значений величины С (или m ) с ненулевой плотностью вероятности; ц и a — математическое ожидание и среднеквадратическое отклонение a ₀; a_K и Р^ — параметры масштаба и формы распределения Вейбулла величины K . Исходные данные задачи приведены в таблице 2.

Таблица 2. Расчетные параметры численного решения

Название параметра	Тип параметра (детерминированный/вероятностный)	Распределение/значение
Среднее значение внутреннего давления в трубопроводе p , МПа	Детерминированный	8,0
Коэффициент асимметрии цикла нагружения	Детерминированный	0,9
Размах давления за цикл нагружения Д р , МПа	Детерминированный	0,8
Начальная глубина трещины a , м	Вероятностный	Нормальное N ( 1 - 10 " 3,1 - 10 " 4 ) или экспоненциальное Exp (У ( 1 - 10 - 3 ) )
Параметр C уравнения Пэриса, м/(цикл(Па·м1/2)- m )	Вероятностный	Равномерное U ( 2,7 - 10 - 11; 3,1 - 10 - 11 )
Параметр m уравнения Пэриса	Вероятностный	Равномерное U ( 2,8; 3,2 )
Радиус серединной поверхности r , м	Детерминированный	0,63
Постоянная толщина стенки 3 , м	Детерминированный	0,025
Окружное напряжение a , МПа	Детерминированный	201,6
Вязкость разрушения K , МПа·м1/2	Вероятностный	Вейбулла W ( 62,2; 30,0 )

Используя описанную выше процедуру, основанную на методе статистических испытаний Монте-Карло, можно построить зависимости вероятности разрушения от числа циклов нагружения для различных вариантов расчета (Рис. 5). Кривая 1 получена с помощью упрощенной аналитической зависимости (23). Кривые 2 и 3 соответствуют двум уточненным численным решениям, учитывающим поправку на кривизну поверхности элемента, изменение глубины трещины в процессе циклического нагружения, а также статистический разброс параметров уравнения Пэриса C и m и вязкости разрушения K . При этом кривая 2 описывает случай, когда величина «начальная глубина трещины» распределена по экспоненциальному закону a ₀ ~ Exp (У ( 1 - 10 - ³ ) ) , а кривая 3 — случай, когда закон распределения нормальный: a ₀ ~ N ( 1 - 10 ^{- 3} ; 1 - 10 ^{- 4} ) . Сопоставление кривых 1 - 3 свидетельствует, что упрощенная аналитическая зависимость дает достаточно точную, хотя и неконсервативную, оценку вероятности разрушения при экспоненциальном законе распределения начальной глубины трещины.

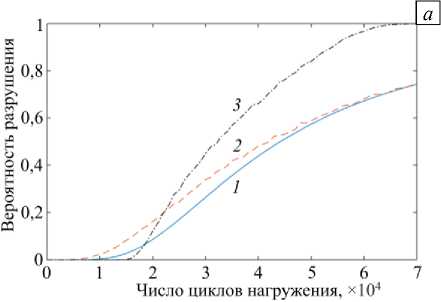
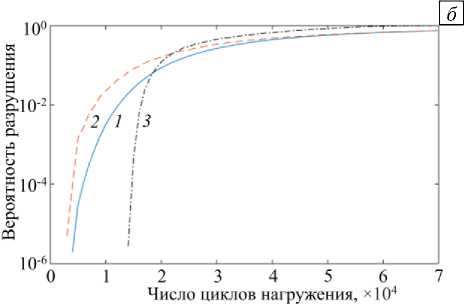
Рис. 5. Зависимости вероятности разрушения от числа циклов нагружения в линейных ( а ) и полулогарифмических координатах ( б ) для различных расчетных случаев: по аналитической формуле (23) (кривая 1 ), численное решение с экспоненциальным ( 2 ) и нормальным ( 3 ) законами распределения a

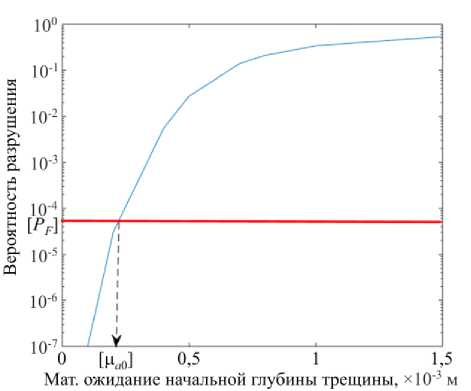
Рис. 6.    Зависимости    вероятности    разрушения от математического ожидания начальной глубины трещины

На рисунке 6 для рассматриваемого расчетного случая представлена полученная на основе численного решения зависимость вероятности усталостного разрушения от величины математического ожидания начальной глубины трещины ц после N = 20000 циклов нагружения. Из приведенного графика следует, что расчетная вероятность весьма чувствительна к величине начальной глубины трещины. С практической точки зрения это означает, что для обеспечения прочностной надежности конструктивного элемента, взятого в качестве исследуемого, необходимо обеспечить такое качество выходного дефектоскопического контроля, при котором математическое ожидание пропускаемых в эксплуатацию дефектов не будет превышать предельно допустимую величину [ц a ] .

• 4.    Заключение

Разработаны оригинальные многофакторные аналитический и численный подходы для оценки вероятности усталостного разрушения элементов трубопроводов, позволяющие учитывать неопределенности, связанные со стохастической вариативностью начальных размеров трещин, с вязкостью разрушения и параметрами уравнений, описывающих кинетику трещин при циклическом нагружении. Полученные решения справедливы для тонкостенных труб, но могут быть распространены и на толстостенные трубы, но при условии использования соответствующих формул для нахождения коэффициентов интенсивности напряжений.

Сравнение результатов аналитического и численных решений позволяет сделать вывод о том, что приближенная аналитическая оценка вероятности разрушения применима для проведения предварительных расчетов на этапе проектирования конструктивных элементов, а также для получения априорных оценок вероятности разрушения при определении объема и периодичности проведения инспекций состояния рассматриваемых элементов при реализации риск-ориентированных подходов к обеспечению их прочности и безопасности.

Впервые показано, что расчетная вероятность разрушения оказывается весьма чувствительной к изменению математического ожидания глубины исходной трещины и типу распределения этого параметра, что говорит о важности обеспечения точности входного контроля при вводе в эксплуатацию исследованного элемента с целью исключения элементов, содержащих дефекты, которые в течение интервала времени до очередного неразрушающего контроля могут достичь критического размера.