Аналитические и численные решения начально-краевых задач волнового движения воды в водохранилище
Автор: Созанов Валерий Гаврилович, Музаев Илларион Давидович, Макаров Сергей Александрович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.5, 2003 года.
Бесплатный доступ
Поставлены и решены начально-краевые задачи волнового движения воды в водохранилище при вторжении в него обвально-оползневого массива или лавинообразного потока. Используется линейная и нелинейная теория поверхностных гравитационных волн в идеальной несжимаемой жидкости. Получены расчетные формулы для определения скорости вторжения в водоем лавинообразного потока и амплитуды образовавшейся волны.
Короткий адрес: https://sciup.org/14318082
IDR: 14318082 | УДК: 532(075.8)
Текст научной статьи Аналитические и численные решения начально-краевых задач волнового движения воды в водохранилище
Для потенциального движения rot U = 0.
Вводя потенциал средней по ширине скорости Ф(ж,гД) из выражения (38) легко получаем интеграл Коши в линейном приближении
ЭФ Р
-+gz+- = №
Компоненты средней по ширине скорости выражаются через потенциал Ф(ж,гД) в виде
— ЭФ ЭФ и = gradФ, Ux = —, Uz = —. (41)
Пусть z = г/(жД) — уравнение осредненной по ширине волновой поверхности. Тогда при отсутствии внешнего давления на свободную поверхность выражение (40) для z = ?/(жД) принимает вид куда величина т/(жД) входит неявно. Однако, как это принято в линейной теории волн Коши — Пуассона (где г//А <С 1, т. е. амплитуда волны мала по сравнению с длиной волны), выражение (42) можно записать следующим образом:
ЭФ(ж, 0,1) di
+ gy^x, 1) = 0.
ГВ1 Э¥у
Jb, 9у
В результате такого осреднения, называемого методом Буссинеска, уравнения (30) примут вид:
(27)-
1(ВРД = А^рв^у Л^р. at pax р ох
= —дВ - -у(РВ) + at р az р az д д
— (,UXB') + — (UZB) = дД,гД),
OX OZ где приняты следующие обозначения:
B2
В-2
Р(ж, z, t)
В2
В линейном приближении имеет место равенство
НДж, ОД) = —
ЭФ(ж, 0,1) dz
Дифференцируя выражение (43) по t и подставляя в него (44), получаем
У2Ф уф
~ЭС+97к “°
при г = 0.
С учетом (41) уравнение (39) примет вид div (В grad Ф) = q,(46)
или в развернутом виде
У2Ф у2ф 1 УВ УФ 1 ЭВ ЭФq
--1---1-----1----=(47)
Эх2 ЭД В Эх Эх В dz dzВ
В классической теории волн Коши — Пуассона потенциал скорости удовлетворяет дифференциальному уравнению Лапласа [1-4]. Здесь же дополнительно появляются три члена, из которых два последних члена левой части связаны с непризматическим очертанием водоема. Правая часть связана с боковой приточностью или со скоростью вторжения в водоем обвально-оползневого массива или потока селевого либо лавинного характера.
При выводе дифференциального уравнения (47) используются упрощающие допущения 1 и 2. Аналогичные допущения принимаются для вывода дифференциальных уравнений одномерного неустановившегося движения воды в непризматическом русле (плавно изменяющееся движение воды). В отличие от метода Буссинеска, гидродинамические уравнения Эйлера усредняются не по полному живому сечению потока, а лишь по ширине водоема. Дифференциальное уравнение (47) дает возможность решить широкий круг задач, связанных с волновым движением идеальной несжимаемой жидкости в узких непризматических водоемах.
Рассмотрим частный случай, когда боковой приток q = 0 и ширина водоема ВД,г) изменяется по экспоненциальному закону
ВД, z') = Bq exp(si$ + s^zY
В этом случае коэффициенты дифференциального уравнения — постоянные числа si и 82, поэтому можно провести систематический анализ влияния очертания непризматич-ности водоема на характеристики волнового движения жидкости.
Подставим выражение (48) в (47), при q = 0 получим
У2Ф у2ф уф уф
о 9 + о 9 + 81Щ--Ь ’АДГ" — 0.
Уж2 dzz Эх dz
Граничные условия на свободной поверхности z = 0 и на дне z = — Н имеют следующий вид:
У2Ф уф
УФ
при z = 0, при z = —Н.
Решение уравнения (49) можно представить так
Ф(ж,гД) = е "з^фДж^Д).
Подставим (52) в выражения (49)—(51), получим
|
Э2Ф у2ф Эх2 Эг2 |
ЭФ 82 Щ-- UZ |
-^Ф1 = °: |
(53) |
|
Э2ФХ ЭФ1 utz UZ |
= 0: |
(54) |
|
|
ЭФ1 dz |
= z=-H |
0. |
(55) |
Частное решение дифференциального уравнения (53) представим в следующем виде:
Ф(ж,г4) = Ф0(г)ег(,гж
Подставим выражение (56) в (53)—(55), получим
с/2 Фр с/Фр dz2 2 dz
^2 + ^) Фо = 0:
9т , х dФo(z^
— сюФоД) + g--;--- = 0 при z = 0;
dz
^O(^) n тт
-----= и при z = —Н.
dz
Далее имеем
Фр (г) = С^АС^\ (60)
где
Подставим выражение (60) в граничные условия (58) и (59), получим с2 = -С1^е-(Л1-Л2)я
А2
-А1Я
Ф0Д) = Ci—---(А2еЛ1(я+г) - А1еЛ2*я+г)), (63)
А2
ст2(А2еЛ1Я - А1вЛ2Я) + дА1А2(еЛ1Я - еЛ2Я) = 0,
/ еЛ1Я_еЛ2Я
" = \)9X1X2 А2еЧЯ_А1еА2я-
Подставив значения Ai и А2 из (61) и (62) в (63), найдем фазовую скорость
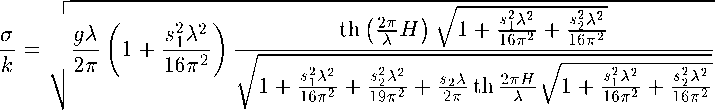
где А = ^ — длина волны.
При si = 0 и S2 = О из выражения (64) получается общеизвестная формула для фазовой скорости в призматическом бассейне [1-4].
С =
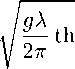
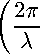
При Н —> оо выражение (64) упрощается и принимает вид
С =
g A / Г S?A2 SoA2 82 А
— 1 /1 j --1--1-- А---
2% \ V 16тг2 16тг2 4%
Анализ этой формулы показывает, что параметр непризматичности, в продольном направлении si незначительно влияет на фазовую скорость волны, а параметр 82, характеризующий переменность ширины водоема в вертикальном направлении, — существенно.
При 82 = 0 для семейства линий тока получается уравнение
2 =
4а2
, 1 S1 2тг
In 1 + ^ tg у Ж
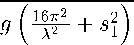
При допущении si = 0 выражение (67) принимает вид:
2%
2 = ——In COS—ж + const, 2тг А что представляет собой уравнение линий тока для призматического водоема.
Связь между длиной А и периодом волны Т получается в виде:
V64?r2 - s^2T2'
Легко заметить, что при выполнении условия волна с периодом Т неустойчива. Этот фактор, по-видимому, можно использовать при конструировании волногасящих сооружений.
Волновое движение воды в узких глубоких непризматических водохранилищах вызванное вторжением обвально-оползневых массивов либо лавинообразных потоков описывается дифференциальным уравнением
52ф у2ф г QB дф 1 ЭВ ЭФ _ q(x,z,t)
Эх2 dz2 В Эх Эх В dz dz В ’ и следующими начальными и граничными условиями
ЭФ
Ф = — = 0 при t = 0, (72)
|
ЭФ |
= 0. |
ЭФ |
= 0. |
|
|
— |
— |
|||
|
Эх |
ж=0 |
Эх |
x=L |
|
|
ЭФ |
= о, Z=-H |
/д2Ф ЗФ\ |
= 0, ^=0 |
|
|
dz |
||||
где В(ж,г) — ширина водохранилища, q^x,z,t) — скорость вторжения в водохранилище обвально-оползневого массива или лавинообразного потока.
Подставим B(x,z) из (48) в (71) и применим подстановку
Ф(ж,г,1)=е “з^ф^ж^,#),
тогда выражения (71)—(74) примут вид
|
Э2Ф1 |
д2Ф1 |
ЭФ1 |
s2 qA^A s_lt S9- |
|
дж2 |
-1-- dz2 |
+ s2~5— dz |
— —Ф1 = —-—-—-— -p 2 ^ . e 2 4 1 Bq |
|
ж 1 9Ф1 |
|
|
ф1 =0’ |
= 0, |
|
t=o dt |
t=o |
ЭФ1
Эх
^^^^^^^™
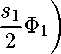
= 0, ж=0
ЭФ1
Эх
^Ф, 2
= 0, x=L
ЭФ1 dz
= 0, г=-н
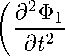
эфа
+ 9^ Эг /
= 0.
-=о
В результате введения дифференциального оператора э В pM = T^ + ^ + s2T"T(
Эх2 Эг2 Эг 4
и применения подстановки
ЭФ| si
^-^Ф1 = ^(Ж,Щ^)(81)
Эх 2
начально-краевая задача (76)—(79) приводится к следующему виду
Э Мх-^А _чт _S9-\ s-vq^x.z.t^ _чт _s„z
DW = aiA"^e 2 е W~B^e 1’
|
^ t=0 ^: |
Э'ф "dt |
= 0, t=o |
(83) |
|
>(ж, z, t) = 0. ж=0 |
ф^х, z,tp = 0. x=L |
(84) |
|
|
IT =0’ 82= = -H |
/ Э^-ф Э-ф\ ( ЭВ + 9"dz ) ” °' \ ut / ~=0 |
(85) |
|
Начально-краевая задача (82)—(85) решается теми же методами, которые были ис пользованы при решении задачи (1)-(6).
В частном случае при допущении 82 = 0, для волновой поверхности воды в водохранилище получается следующее выражение
2 Vo - si
--------е 2
gLB0
cos где
In = Vg^nthXnH, Xu = у a^ + у, an = ^, p+a p+a
Ацп = e 1 • cos(anx) dx, J2,n = e 1 ■ sm(an$) dx.
J XQ — a J x^ — a
Прогнозирование устойчивости откосов является необходимым элементом изучения оползнево-обвальной лавины, ибо при высокой степени устойчивости откосов необходимость расчетов по определению последствий явлений оползне-обвальной природы отпадает. Кроме того, оценка статистической устойчивости является необходимым условием последующего динамического расчета возможного ЛОП, ибо им определяется масса обвального тела.
Известно, что материал оползневых склонов представляет слабо связанную горную породу, имеющую следующие физико-технические характеристики: угол внутреннего трения р, коэффициент сцепления с, коэффициент эффективной вязкости г/, порог ползучести то, плотность р, и модули упругости Е и G. Эти характеристики определяются лабораторно-полевыми исследованиями. Некоторые из них представлены в виде графиков в зависимости от влажности грунта [6, 7].
Очевидно, что в допредельном состоянии склон может находиться в чисто упругом деформированном состоянии. Дифференциальные уравнения равновесия в напряжениях имеют следующий вид [6, 7]
Э^х Этху . , , ,
—--h —- = pg sin a + kspg cos Д + a), ox Oy
Эт1у 9oy .
+ —^ = pg cos a - kspg sin a + 7 , ox oy где приняты следующие обозначения: <тх и 07 — нормальные напряжения относительно осей хну соответственно, тху — касательное напряжение, a — угол наклона оползневого склона к горизонту, ks — «сейсмический коэффициент» (коэффициент сотрясения)
as ks = — (as — сейсмическое ускорение), g a — угол наклона оползневого склона к горизонту, 7 — угол атаки сейсмической инерционной силы.
Пренебрегая влиянием концевых эффектов на напряженное состояние массива, можно считать, что напряжения не зависят от координаты х, и тогда выражения (88) преобразуются к виду жу = pg sina + kxpg созД + Д, (89)
dy do.y 7 ' / ।1
-
—= pg cos а — kspg sin(a +
Граничные условия для напряжения будут иметь следующий вид тЖу = 0 при у = О,(91)
Оу = 0 при у = 0.(92)
Интегрируя уравнения (89) и (90) с учетом граничных условий (91) и (92) получим:
TXy = оу = (pycosa-fcspysin(a + 7))y,(94) тху < tg роу + с.(95) Подставим выражения (93) и (94) в (95) получим: \pg sin а + kspg cos(a + у)]у < tg р\рд cos а — kspg sin(a + у)]у + с. Отсюда получается py[sina + ks cos(a + у)]у — tg р\рд cos а — kspg sin(a + y)]y < c. Мощность критического предельного состояния оползневого склона определяется по следующей зависимости ц _ _________________________________ р py[cos a(tga - tg Если критическая мощность больше мощности оползневой толщины склона (расстояние от свободной поверхности склона до коренных пород), то склон будет находиться в допредельном состоянии. При выполнении условия Н^р < Hq оползневой склон может перейти за предельное состояние, т. е. Тху > tg ро.у + С. Динамические расчеты оползней-обвалов иногда осуществляются, исходя из упрощенных уравнений гидродинамики для сильно вязких жидкостей, обладающих пороговым напряжением сдвига, а в некоторых моделях учитывается еще и кулоновское трение. В большинстве случаев такие подходы сугубо приближенные, так как в представлениях их физико-механической структуры кроются непреодолимые противоречия. Тем не менее, даже такие подходы имеют право на существование в качестве грубых аналогов для совершенствования модели и в качестве полезных наводящих положений при построении решений, которые обычно трудны, ибо в таких моделях учитывается и нестацио-нарность, и пространственная двухмерность. В работе рассмотрены две такие тестовые модели, описываемые уравнениями в частных производных, в условиях действия периодической сейсмической силы и зависимости коэффициента вязкости от высоты, причем построены и аналитические, и численные решения. Однако, в качестве основного оперативного средства анализа используется система уравнений для композиционных сред, данная в монографии [10], которая для твердой грунтовой компоненты получена на основании системы уравнений Коши для сплошной среды в напряжениях (в переменных Эйлера), уравнения неразрывности в форме Эйлера, уравнения предельного состояния для сыпучей среды с углом внутреннего трения и коэффициентом сцепления, отвечающего условиям Кулона — Треска — Сен-Венана и уравнения Ишлинского — Гениева, выражающего совпадение направления наибольшей скорости деформации сдвига с одним из направлений семейства линий скольжения. Для жидкой компоненты, которой заполнены поры грунта, содержащей еще мелкодисперсную глинистую примесь, используется известная система двухмерных уравнений Генки — Илюшина. Путем суммирования этих систем исключаются компоненты силового взаимодействия между твердой и жидкой составляющими, и путем введения понятия плотности дисперсоида композиционной среды р, ее скорости и, как для смеси по А. Н. Колмогорову, и давления для смеси, по Н. А. Слезкину, система приводится к гидродинамической форме для двухмерного движения (Т. Г. Войнич-Сяноженцкий, 1970) [8] 0 0 00 Р -KT^pW^ + — VpW^ + -^-^pWx • Ж) = pFx ——-at Эх azЭх d fo Г Z1 , , t0]M , s sin + ^[Ч'-|1-8) + ^дт +----ViTnI----) 8_ / Г , _ . т0 ^ (2E± , ^Ж^ sA+dmyf^^ dz ( г 8 Я* J \ dz Эх / Д + А2 J ’ 0 0 00P ■yr^pW^ + — (рИфЖ) + — (рЖ)2 = pFx —— dt Эх dzdz 9 U т0 1 (dWx ЭЖA . sA sin s) A 1 + эА+ ) + яЛ"эГ + ^т) +--------) (97) а Г г то 1 аж . s sin РфХ 1 + | [2„(1 -,) + —]— +1. = о.|98) dt Эхdz где Н* — параметр Генки, N — параметрическое выражение условия Ишлинского — Гениева, которое для движений без внутренних разрывов при соблюдении условий 4^- у> ~ ~9х Равно — ctg^ и это упрощающее представление принимается ниже как для оползне-обвальных, так и снежных или селевых лавин. Система (96)—(98) используется как базисная для получения одномерных уравнений посредством классической процедуры Буссинеска для однокомпонентных водных потоков. При такой редукции получается следующая система в приближении Сен-Венана ^-(«ppW2^ + -^-^aopW2^ + 7 at Эх ^^^^^^^™ 2s • sin2рД8 — 1 + sin2 7)1 ,,9h — COS'Фri —-Эх ^^^^^^^™ yh г ^^^^^^^™ s/ cos I I ■ I I 1 + 2/2 7 + То + К 8 COS (р — sin2 2<р 4(1 + sin2 <р) _ (1 - s)yW2 = 0, д^ d^pWh^ dt я — PiQii Эх (ЮО) в которой / = tg <р — коэффициент кулоновского трения, h — толщина тела оползня-обвала, W — средняя по h скорость оползневой лавины; д8, ч™, д — объемные веса грунта, воды и композиционной среды, ф — угол наклона поверхности скольжения к горизонту, г = sini/у s — средняя по h концентрация грунта в теле оползня, ар и qq — коррективы Буссинеска; р^ — интенсивность путевого захвата (расхода) грунта оползнем-обвалом. Система (99)—(100) редуцируется в интегральную форму путем интегрирования по продольной координате, что с учетом нулевой толщины у переднего и заднего фронтов лавины и аппроксимации вогнутой поверхности скольжения экспоненциальной зависимостью позволяет свести систему (99)—(100) к одному обыкновенному дифференциальному уравнению Ц^У^-цфуРуидкл^Хад, (юн g№ Ip V 2 / I V 4Р 7 в котором ж — продольная координата центра массы тела обвала объемом U и продольной протяженностью I; гн — начальное значение уклона поверхности скольжения, Dy и £>2 — постоянные, учитывающие физико-механические характеристики композиционной среды: Dx sf 7s - 7w I I ■ I I 1 + 2/2 7 = const, p2 = - + Кs 9 sin2 --- cos to----------x—- 7 [ 4(1 +sin2 = const. (Ю2) (ЮЗ) Здесь объемная концентрация грунта может приниматься в зависимости от конкретных условий равной: s = 0.6 — 0.75, tq — пороговое напряжение сдвига, обусловленное наличием мелкодисперсных глинистых фракций в порах грунта, заполненных водой. Решая уравнения (101) для величины скорости движения W = ^, получим выраже ние —W2 = sh - е-р2^ 2g p2i V 2 7 (Ю4) - ^^ • ^-(1 - e"V^ - D^x2 - D^x. 81 P2 21 В (104) W = 0 не только при ж = 0 (начальное условие), но и при некотором ж = жт, определяемом по (104), при принятии в нем W = 0, которое соответствует дальности выноса и остановки оползня-обвала на уполаживающемся склоне. Наряду с некоторыми другими случаями наиболее опасным проявлением ЛОП оползне-обвального происхождения в горных условиях представляется ситуация, когда срыв неустойчивого откоса с высокой береговой террасы придает такую кинетичность ЛОП, что последний в состоянии перекрыть небольшую горную реку вместе с поймой, создав на ней завальную плотину значительного объема и высоты (рис. 1). При снеготаянии такая завальная плотина образует водохранилище, которое при про рыве создает непредвиденную волну прорыва, угрожающую всем ниже расположенным объектам. Возможны разрушительные последствия для береговых коммуникаций, зданий, ЛЭП, водозаборных сооружений и т. д. полученные на основании развитой теории соотношения позволяют определить силовое воздействие ЛОП на защитные сооружения. Начально-краевая задача (1)-(6) в нелинейной постановке решена конечноразностным методом. В этом случае уравнение (1) начальные условия (2) и граничные условия (3) и (4) остаются в силе. Остается в силе и граничное условие на дне схематизированного водоема. Рис. 1:1 — оползневой откос; 2 — конфигурация оползня-обвала, образованного потерей устойчивости откоса полотна автодороги; 3 — первоначальная конфигурация откоса с полотном автодороги с подпорной стенкой 4, 5 — русло реки; 6 — береговые полосы-полупоймы. В качестве граничных условий на свободной поверхности воды принимаются следующие выражения [9] 91 2 Эш \ Эш\ Uto — + — + — Эх ) \Эу ) \dz -9^^,^ = 0 Эу Эу Эш Эв Эш Эш , х + = при 7 = г/(ж,уА). Эт Эх Эх Эу Эу Эг В результате применения замены переменной [11] z^H % — ----------- Н + уД, у, 1) ’ (Ю5) (Юб) (Ю7) подвижная граница z = уД,у,^ закрепляется, при —Н ^ z ^ уД,у,^, 0 < / < 1. С целью упрощения алгоритма решения задачи и программы расчета на ЭВМ выражения (106) заменяется на следующее Эу _ 9V J _L — az + Эх dip —az. Эу (Ю8) 9t Jo Сравнение численных результатов, полученных представленными выше двумя методами, в широком диапазоне изменения динамических характеристик обвальнооползневого массива и геометрических размеров водохранилища, нелинейные слагаемые весьма незначительно корректируют амплитуду образованной волны в сторону увеличения. В связи с этим можно заключить, что линейная теория достаточно точно для практических расчетов описывает волновое движение воды в водохранилище, вызванное обвально-оползневыми явлениями либо лавинообразными потоками.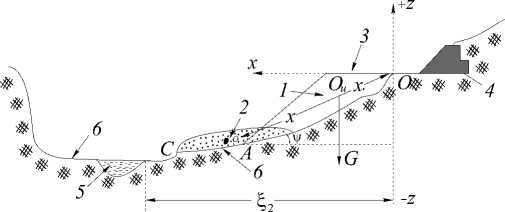
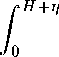
Список литературы Аналитические и численные решения начально-краевых задач волнового движения воды в водохранилище
- Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика. Ч. 1.-М.: Физматгиз, 1963.-727 с.
- Ламб Г. Гидродинамика.-М.: Гостехизат, 1947.-928 с.
- Стокер Дж. Дж. Волны на воде.-М.: ИЛ, 1959.-617 с.
- Мамрадзе Г.П., Музаев И.Д. ВОЗНИКНОВЕНИЕ ВОЛН В ВОДОХРАНИЛИЩЕ ВСЛЕДСТВИЕ ОПОЛЗНЕВЫХ ЯВЛЕНИЙ // Bulletin of the Georgian Academy of Sciences. 1971. Т. 64. № 2. С. 115-120.
- Музаев И. Д., Созанов В. Г. К теории поверхностных гравитационных волн Коши -Гуссона в узких непризматических водоемах//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. 1995. № 3. С. 40-47.
- Соколовский В. В. Статика сыпучей среды.-М.: Физматгиз, 1954.-315 с.
- Маслов Н. Н. Механика грунтов в практике строительства (оползни и борьба с ними).-М.: Стройиздат, 1977.-318 с.
- Войнич-Сяноженцкий Т. Г., Созанов В. Г. Лавинообразные потоки. Возникновение, динамика и воздействие на окружающую среду.-Владикавказ: Изд-во СОГУ, 1997.-221 с.
- Шокин Ю. И., Хакимзянов Г. С. Конечно-разностный метод расчета вихревых и потенциальных течений жидкости со свободной поверхностью//Сборник научных трудов "Вычислительные технологии".-Новосибирск, 1994.-Т. 3, № 8.-C. 133-143.


