Аналитический и компьютерный расчет аберраций высших порядков центрированных оптических систем: 4. Организация расчета аберраций системы
Автор: Бобров С.Т.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы компьютерной оптики
Статья в выпуске: 12, 1992 года.
Бесплатный доступ
Рассмотрены необходимые преобразования полученных ранее формул для обеспечения расчета аберрационных коэффициентов оптических систем. Приведен пример аберрационного анализа конструкции фокусирующего объектива.
Короткий адрес: https://sciup.org/14058262
IDR: 14058262
Текст научной статьи Аналитический и компьютерный расчет аберраций высших порядков центрированных оптических систем: 4. Организация расчета аберраций системы
-
4. ОРГАНИЗАЦИЯ РАСЧЕТА АБЕРРАЦИЙ СИСТЕМЫ
В предыдущих статьях были получены коэффициенты волновых аберраций тонких оптических элементов на асферических поверхностях вращения [1] и формулы преобразования этих коэффициентов при переходе с одной из таких поверхностей на другую [2]. Полученные соотношения обеспечивают расчет аберраций центрированной оптической системы, однако необходимо увязать их в единую методику, позволяющую осуществить расчет наиболее удобным образом.
Установим вначале набор параметров, которые должны быть известны для каждой оптической поверхности системы (или для каждого оптического элемента: поскольку рассматриваются тонкие элементы, то эти два термина означают одно и то же). К первой группе необходимых параметров относятся прежде всего параметры формы поверхности: радиус Tj в вершине поверхности и коэффициенты асферичности CT3j—o7i, где i - номер элемента. Предпочтительно пользоваться обратным радиусом, т.е. кривизной поверхности с. — 1/г;, которая равна нулю для плоскости. Что касается коэффициентов асферичности, то более универсальными (т.е. пригодными для любой асферической поверхности, включая планоид) являются размерные коэффициенты [1], но оперировать удобнее с нормированными [1], величины которых, как правило, ближе к единице.
Кроме того, в эту группу параметров входят расстояния вдоль оси между вершинами поверхностей: расстояние d. j от предыдущей поверхности до рассматриваемой и dj от рассматриваемой поверхности до последующей (см. рис. 1), а также показатели преломления среды до и после поверхности п. и д (напомним, что для дифракционных линз принимается П; = П; = 1).
Ко второй группе параметров (в отличие от первой рассчитываемых, а не задаваемых изначально) относятся отрезки оптической поверхности sje s-, которые определяются по следующим формулам (с учетом правила знаков, принятого в оптике):
-
1 = __- (1)
si ^di-l^-’l ,
=Л = i.
-
si si fi J .
Первое из соотношений (1) представляет собой тривиальное геометрическое соотношение s^s^j-d^, (см. рис. 1), но преобразованное таким образом, чтобы использовались только обратные отрезки, т. к. сами отрезки мо-
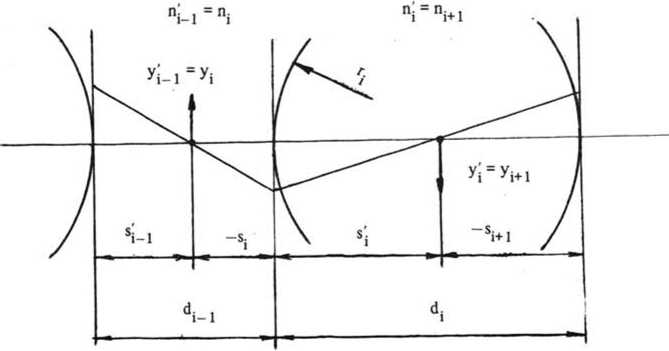
Рис. 1. Параметры i-го оптического элемента в осесимметричной оптической системе.
Показан ход предметного нулевого луча гут быть бесконечными для некоторых поверхностей. Второе из выражений (1) является обобщенной формулой отрезков, которая может применяться как к преломляющим поверхностям, так и к дифракционным линзам. В первом случае заднее фокусное расстояние рассчитывается как
1= ±Л
f: n:rj что следует из первого соотношения (8) в работе [ 1 ].
Во втором случае оба показателя преломления принимаются равными 1, а заднее фокусное расстояние равно:
4=S?L(4-±) (3)
fi Х0 Zi Zi в соответствии с первым из соотношений (12) в [1], где гу zj - отрезки записи дифракционной линзы; XQ. X -длина волны записи и рабочая длина волны; m — порядок дифракции.
Формулы (1) носят рекуррентный характер и могут использоваться в различной последовательности в зависимости от постановки задачи. Если известен передний отрезок системы s, то он же является и передним отрезком первой поверхности sp с которой и следует начинать расчет. Если известен задний (выходной) отрезок системы s', то он же является задним отрезком последней k-й поверхности, и расчет следует вести в обратной последовательности. Наконец, возможен случай, когда заданы оба отрезка системы, а в ее составе предусмотрен дифракционный корректор, т.е. дифракционная линза, обеспечивающая оптическое сопряжение предмета и изображения. В этом случае необходимо вести расчет отрезков от первой и последней поверхностей до корректора, заканчивая вычислением его отрезков.
Теперь рассмотрим форму представления аберрационных коэффициентов оптических элементов, составляющих систему. В соотношениях (9-10, 13-14) работы [1] эти коэффициенты даны для случая, когда аберрации выражены в координатах изображения, формируемого самим элементом (х,1, у.). Для разных поверхностей системы эти координаты не совпадают, кроме того, для какой-либо поверхности они могут оказаться бесконечными. Чтобы избежать указанных трудностей, преобразуем аберрационные коэффициенты всех поверхностей системы, выразив аберрации каждой из них через координаты изображения, формируемого системой в целом (х', у). Для 3-го порядка, например, новые коэффициенты будут выражаться через старые следующим образом:
-
S3i = S3i: C3i = ^i^^ *31 = *31 ^.^; , 0)
F3i = F31<7)2- ЙЦ^З!^)3'
Из формул работы [ 1 ] нетрудно убедиться, что коэффициенты полевых аберраций тонких оптических элементов содержат величину п^ (для дифракционной линзы 1 /sj)e степени, соответствующей степени полевой координаты в данной аберрации. В итоге во все коэффициенты полевых аберраций в указанной степени войдет величина х,-^^. (5)
^У v которая является инвариантом для данной поверхности, т.е. сохраняет свое значение при замене np st, yj на Пр $р у..
Расчет инвариантов X ведется по рекуррентной формуле:
si , s. + d. . d. .
X. = ^ -н- = х.., = V1 (I ), (6)
начиная с последней поверхности, для которой эта величина, как следует из (5), равна Xk = n^/s^ = n'/s’. Ясно, что в качестве единой полевой координаты можно выбрать и координату предмета или любого промежуточного изображения в системе. В этом случае меняются только стартовая точка и направление расчета инвариантов X.
Описанное преобразование коэффициентов аберраций позволяет представить их в форме, симметричной относительно п.', s.' и п., s.. Приведем в качестве примера выражения для модифицированных коэффициентов 3-го порядка преломляющей асферической поверхности, которые имеют вид (ср. с формулами (9) в [1 ], индекс i и тильду опускаем):
S3 = “‘л <4т " J n s ns
с = X ■ 1А (4т - -); 5 А n s ns
А3 = -X2 (4т " — n s ns
F3 = "х2,а<А -4): D3 = X3(-L - -Ь
3 Л n2 n2 n2 n2
Напомним, что величина 1Д = (n'/s' — n'/r) является инвариантом поверхности (инвариант Аббе), что следует хотя бы из выражения (8) работы [ 1 ].
Полученная форма аберрационных коэффициентов обеспечивает возможность расчета аберраций как в прямом, так и в обратном ходе лучей. В последнем случае следует только поменять местами n', s' и n, s, что приведет к смене знака у всех коэффициентов.
Поскольку теперь аберрации поверхностей системы выражены в единых полевых координатах, то, пересчитав аберрационные коэффициенты одной поверхности на другую, их можно складывать с коэффициентами этой другой поверхности без каких-либо дополнительных преобразований. Необходимо, однако, модифицировать формулы пересчета, полученные в работах [2, 3].
Во-первых, следует определить смысл величин z и t, фигурирующих в этих формулах. Напомним, что z - это расстояние от вершины исходной поверхности до плоскости, в которой располагается центр кривизны аберрированной сферической волны, распространяющейся между поверхностями. Отсюда ясно, что при расчете в прямом ходе лучей, когда требуется перейти с i-й поверхности на (i + I )-ю, таким расстоянием является выходной (задний) отрезок i-й поверхности sj. Величина t в этом случае очевидным образом равна расстоянию между вершинами поверхностей dj. В обратном ходе лучей при пересчете аберраций с i-й поверхности на (i -1)-ю в качестве z следует использовать отрезок s; (причем с обратным знаком), а в качестве t — расстояние dj ^
Необходимо также скорректировать формулы преобразования аберраций с учетом замены обычных коэффициентов на модифицированные [см. (4)]. В качестве примера приведем выражение для пересчета коэффициента дисторсии 7-го порядка из плоскости в плоскость в прямом ходе лучей (ср. с последним из выражений (11) в работе [2]):
D7 = Тн [D? - Т^ (F? + 6А7) + ЗТ2 (ЗС7(3) + 4Z7) -
- T2i <3S7(3) + 24Р7(2) + 8В7) + 51421(ЗС7(2) + 4М?) -
-
- 3T|j (S7C) + 6Р7(2)) + 7Т^С7(1) - T2jS7(1)l
3d. 2d?
" s^/4^ + F5D3 + 2D5A3 + D5F3) - _^-(3C3D32 +
+ 4A32D3 + 4AjF3D3 + Fj^Dj) - ^4 lT3j(2A3D3 + F3D3^ ~ °32 1
Индекс i при аберрационных коэффициентах опушен, поскольку, вообще говоря, речь идет о преобразовании не аберраций i-й поверхности, а суммарных аберраций всех предшествующих поверхностей. Вспомогательные величины в выражении (8) равны:
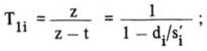
т - 1 yi - ХАТ • *
21 z -1 y' nj 11
T - yi - Xisi .
*3i 7 7"
У n( J
Аналогичным образом надо скорректировать и формулы преобразования аберраций при изменении формы поверхности. Так, соотношение для пересчета коэффициента первой птеры 7-го порядка из плоскости на сферу бу дет иметь вид (ср. с соответствующей формулой (10) из [3]):
P7(l) = P7G) ~ ^^З! С5(1)-2Р5> 15$2г2 <3T3iS3 <Ю)
-
- 14T3iC3 + 5А3) - ^ (T3iC3 - А3) - ^- (S3A3 ♦ 2С2).
Таким образом, введение единых полевых координат и соответствующая модификация выражений для аберрационных коэффициентов и формул пересчета устраняют все трудности, связанные с возможным положением какого-либо промежуточного изображения в системе на бесконечности. Форма представления всех соотношений позволяет, кроме того, легко осуществлять расчет аберраций как в прямом, так и в обратном ходе лучей. В результате становится возможным создание достаточно эффективной программы анализа аберрационных свойств оптических систем.
В качестве иллюстрации тех сведений о системах, которые можно получать с помощью этой программы, приведем результаты исследования свойств весьма простого фокусирующего объектива для лазерного проигрывателя [3], схема которого представлена на рис. 2. Объектив состоит из плосковыпуклой рефракционной линзы и дифракционного корректора аберраций, который расположен со стороны сферической поверхности линзы. Со стороны корректора падает лазерный пучок, фокусируемый объективом. В работе [3] представлены результаты численных расчетов качества фокусировки, которые показывают, что с увеличением оптической силы корректора это качество растет, но при достижении определенного предела оно резко ухудшается, и объектив становится неработоспособным. Использование программы расчета аберраций позволяет дать этому факту наглядное объяснение.
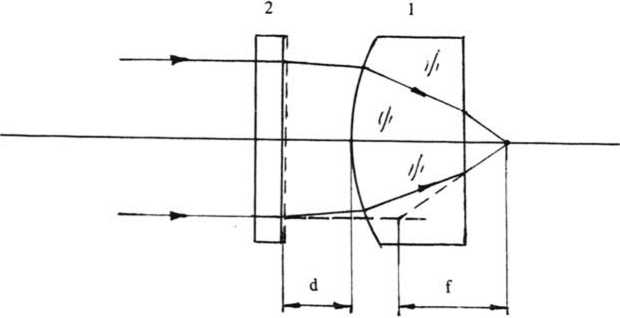
Рис. 2. Оптическая схема фокусирующего объектива: 1 - рефракционная линза; 2 - дифракционный корректор
Поскольку фокусирующий объектив работает в пределах небольшого поля зрения, то качество фокусировки зависит прежде всего от комы 3-го и 5-го порядков. На рис. 3 даны графики изменения этих аберраций (в долях длины волны) в зависимости от расстояния d между рефракционной линзой и дифракционным корректором для трех соотношений между фокусными расстояниями корректора и объектива. Приведены также и зависимости критерия Марешаля (т. е. общего качества фокусировки) от этого расстояния.
Нетрудно видеть, что при наименьшей оптической силе корректора из трех представленных характер изменения комы 3-го и 5-го порядков таков, что при определенном расстоянии d они равны и противоположны по знаку
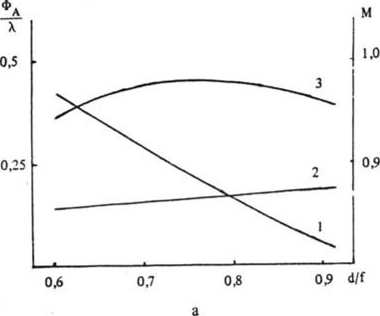
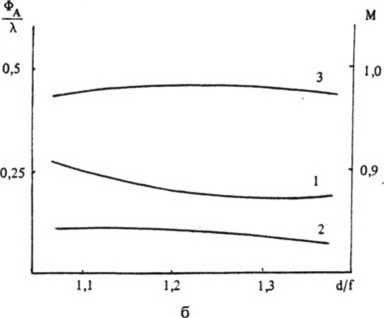
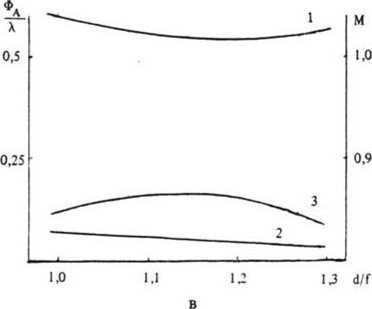
Рис. 3. Зависимости комы 3-го порядка (1), первой комы 5-го порядка (2, величина аберрации отложена с обратным знаком) и критерия Марешаля М (3) от отношения расстояния между компонентами объектива (d) к его фокусному расстоянию (f).
Отношение фокусных расстояний объектива и корректора составляет 0,25 (а) ; 030(6) и 035 (в)
(максимум критерия Марешаля лежит несколько в стороне в силу влияния других аберраций). При увеличении оптической силы корректора равенство абсолютных величин двух ком уже не достигается, но они достаточно близки друг к другу, что обеспечивает высокое качество фокусировки. При дальнейшем увеличении оптической силы корректора величины двух ком значительно отличаются, и качество фокусировки падает.
В приведенном примере аберрационный анализ изменения качества фокусировки не позволил каким-либо образом улучшить объектив в силу его предельной простоты, однако в более сложных случаях расчет аберрационных коэффициентов оптических систем несомненно поможет оптимизировать их конструкции.


