Аналитический расчет основной частоты колебаний многокупольной крыши

• 1    Введение / Introduction

2.1    Схема фермы

Для расчета деформаций и собственных частот сооружений в инженерной практике, как правило, используется метод конечных элементов, реализуемый в различных специальных пакетах [1], [2]. В [3] при расчете пространственной модели антенны для космической связи использовались метод конечных элементов и балочная аналогия. Для расчета простых статически определимых регулярных ферм возможен и аналитический метод. При нахождении прогибов некоторых плоских ферм он реализован в [4], [5]. Нижняя граница основной собственной частоты колебаний плоских ферм в аналитической форме с помощью метода Донкерлея найдена в [6], [7]. Формула для нижней оценки собственных колебаний плоской регулярной фермы с прямолинейным верхним поясом и произвольным числом панелей получена в [8] с помощью системы компьютерной математики Maple. Аналитические решения для пространственных ферм встречаются реже. В [9] получена формула для прогибов пространственного контурного покрытия, треугольного в плане, при действии на него равномерно распределенной по узлам нагрузки. Аналитические оценки первой собственной частоты методом Донкерлея снизу и методом Рэлея сверху получены для шестигранного покрытия купольного типа в [10].

В [11] для нахождения аналитического решения задачи о деформации элементов строительных конструкций используется система компьютерной математики Maple и метод суперпозиции, основанный на разложении по начальным функциям. В [12] для этих же целей применяется метод начальных функций и система Maple.

В справочнике [13] приведены формулы для аналитического решения задач о прогибе различных схем плоских статически определимых регулярных ферм балочного, арочного и рамного типа с произвольным числом панелей. Формулы для расчета прогиба плоских регулярных ферм в системе Maple получены в [14]–[16]. Нижняя оценка основной собственной частоты методом индукции выведена для плоских ферм [17]–[19]. Впервые вопрос существования схем регулярных статически определимых ферм поставили Hutchinson R.G. и Fleck N.A. [20], [21].

В работах Kaveh A. [22]–[24] применительно к задачам оптимизации рассмотрены некоторые общие вопросы анализа регулярных стержневых конструкций. Zok F.W., Latture R.M. и Begley M.R. в [25] используют теорию кристаллографии для классификации периодических стержневых систем. Расчет пространственной периодической стержневой антенной конструкции с заменой фермы на эквивалентную пластину выполнен в [26]. Эта же задача с помощью принципа энергетической эквивалентности и метода конечных элементов решается в [27].

В настоящей работе рассматривается пространственная схема статически определимой конструкции, состоящей из соединенных между собой ферм с шестигранными пирамидальными куполами. Ставится задача вывести формулы для зависимости нижней границы первой собственной частоты от числа панелей. В решении учитываются три степени свободы масс, сосредоточенных в узлах фермы. Численно анализируется спектр собственных частот системы.

2 Материалы и методы / Materials and Methods

Исследуемая конструкция покрытия состоит из n отдельных ферм купольного типа с шестигранным основанием, соединенных между собой в ряд (рис. 1). Ферма регулярная, каждый элемент периодической структуры (панель) состоит из шести стержней купола, шести стержней контура длиной a и шести опорных стоек высотой h . Купол имеет высоту h (рис. 2). Опора A , составленная из стойки и двух горизонтальных связей, эквивалентна сферическому шарниру, опора B представляет собой цилиндрический шарнир. Ферма содержит ^ = 15 n + 6 стержней, включая 4 n + 2 вертикальных опорных стоек.

17=5^2

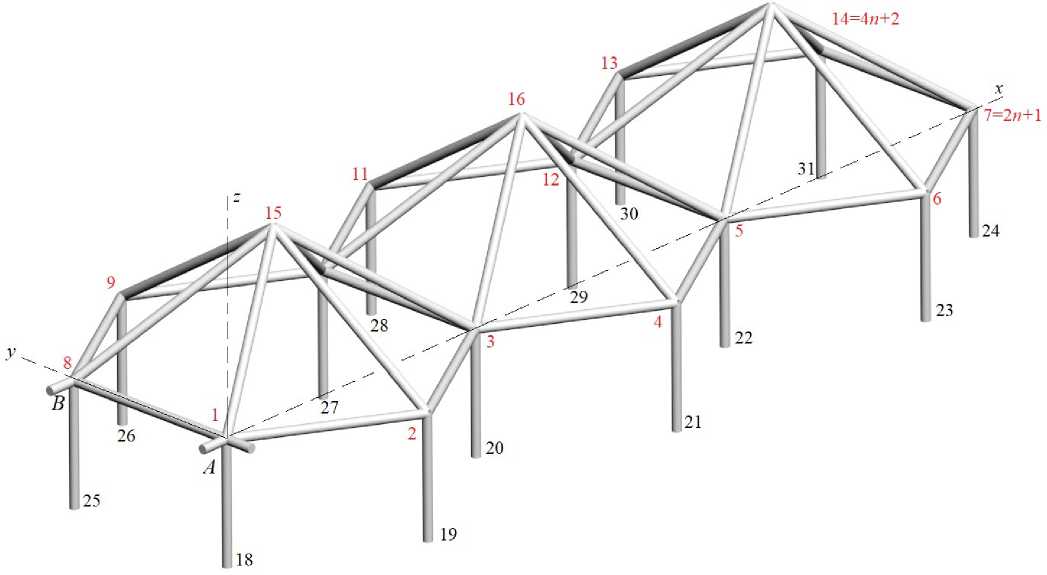
Рис. 1. - Схема фермы, n=3

Fig. 1. - Truss scheme, n=3

Раскосы купола имеют длину c = ■]a ² + hi² . Общая длина покрытия из n панелей na VI. Все стержни конструкции соединены между собой шарнирно. Конструкция статически определимая.

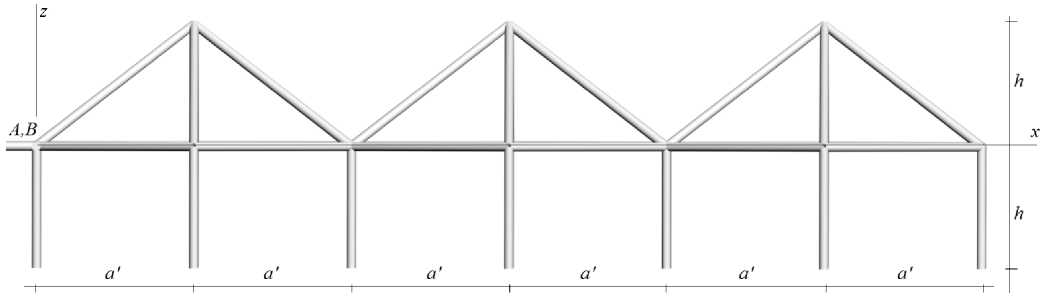
Рис. 2. - Размеры фермы, a ' = a33 /2 , n=3

Fig. 2. - Truss dimensions, a ' = a31/ / 2 , n=3

Расчет усилий в стержнях производится методом вырезания узлов в программе на языке символьной математики Maple [28] . Стержни и узлы нумеруются. В текст программы вводятся координаты шарнирных узлов. Начало координат выбрано в узле A .

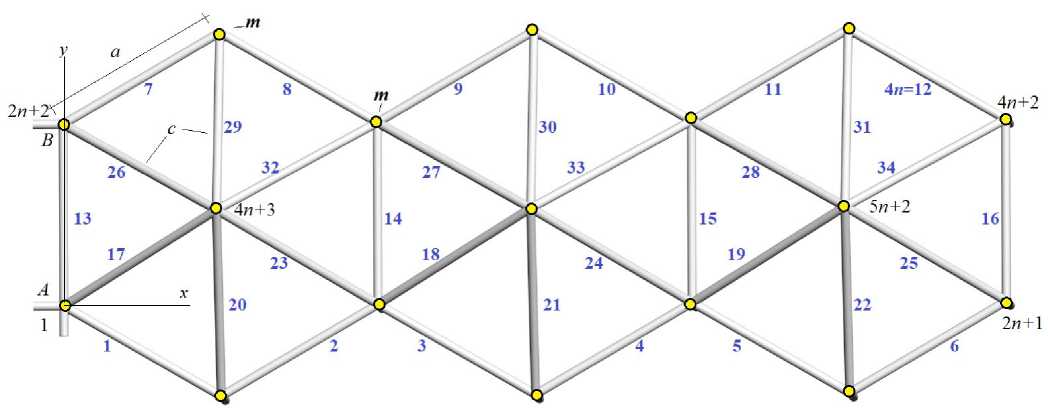
Рис. 3. - Расположение масс и номера стержней, n=3, Fig. 3. - Location of the masses and numbers of elements, n=3

Координаты узлов по контуру конструкции имеют вид:

• x. = x = a ( i — 1)Тз / 2, i       i + 2 n + 1

y. = — (( — 1) i + 1) a /2, z. = z.^ ₊₁ = 0, i                                           i i + 2 n + 1        '

V i + 2 n + 1 = (( — 1) ⁱ + 1) a /2 + a , i = 1,-,2 n + 1.

Координаты вершин:

x = a(2i — 1)\3 /2, y„ „ = a /2, z = h , i = 1,.., n . i +4 n +2                              ’ y i +4 n +2             ’ i +4 n +2        ’         ’ ’

Координаты оснований боковых стоек:

x = x, y = y, z     =—h , i = 1,..,4 n + 2.

i +5 n +2        i    i +5 n +2        i    i +5 n +2

Порядок соединения стержней в узлы вводится в программу при помощи списков номеров концов соответствующих стержней, по аналогии с заданием графов в дискретной математике. Стержни контура, например, имеют следующие номера концов (рис. 3):

Ф = [ i , i + 1], Ф. „ = [ i + 2 n + 1, i + 2 n + 2], i = 1,..,2 n .

i                           i + 2 n

Cписки концов стержней не имеют ориентацию, выбор начала и конца стержня не влияет на решение. Стержни шестигранных пирамид кодируются в двойных циклах:

Ф л ,= [2i - 2 + j,i + 4n + 2], i+(4+j) n+1                        ,                    ,

^Ф i _{+ (7 +} j ) _{n + 1} = ^[2 i ^{- 1 + 2 n +} j , i ^{+ 4} n ^{+ 2}ь i = 1,.., n , j = ^--a

2.2    Расчет усилий в стержнях

Расчет жесткости конструкции, необходимый для определения собственных частот, выполняется по формуле Максвелла – Мора. Необходимые для этой формулы усилия в стержнях определяются из уравнений равновесия узлов в проекции на оси координат x, y, z. Система уравнений равновесия узлов записывается в матричном виде GS=B , где G — матрица направляющих косинусов усилий, рассчитанных по координатам узлов и спискам номеров концов стержней Ф i , i = 1,.., у , S — вектор неизвестных усилий и реакций опор, B — вектор нагрузок на узлы. На каждый узел фермы отводится по три строки матрицы G и три соответствующих элемента вектора нагрузок. В элементы вектора нагрузок Ф, „, Ф, ,, Ф, , где i 3 i 2      3 i 1      3 i

— номер узла, записываются нагрузки на этот узел соответственно в проекции на ось x, y и z . Проекции единичных векторов усилий в уравнениях равновесия узлов на оси координат вычисляются по данным о координатах узлов и порядку соединений стержней в узлах:

I . = (x^     x ) / I, I . = (y^     y ) / I., I . = (Z^ — Z)  ) / I., i = 1,..., n, x,t Ф . Ф »’ y,i Ф Ф »’ z,t Ф . Ф t

^,                         i ,1                   i ,2                        y ^,                        i ,1                   i ,2                            ^,                        i ,1                  i ,2

где l. = ixl\ + l'' + l^ — длина стержня i . В число неизвестных усилий входят усилия в стержнях и реакции опор. Матрица коэффициентов уравнений равновесия заполняется по строкам. Каждые три строки соответствуют одному узлу и уравнениям проекций на оси x, y и z соответственно:

3 Ф i 1 — 2, i

l / l G = l / l ,   G.^

x , i i"       3Ф.. — 1 , i          y , i        i'         3Ф. - , i

’                                      i ,1        ,                    y ,                                           i ,1 ,

= l / 1 , Z , i ' i

G...   9 = — l / l , G

3ФО —2, i           x, i      i*    3ФО —1, i i ,2                                                              i,2

= — l . / l, , G.^ . = -I . / l.

y,i i ’      3Ф. „,i              z,i i i,2

Проекции усилий, приложенных к разным концам одного стержня, имеют противоположные знаки.

2.3    Собственная частота колебаний

Принято, что масса фермы сосредотачивается только в ее узлах равномерно по всей конструкции. Каждая масса имеет три степени свободы. Число степеней свободы рассматриваемой модели фермы K = 3(5 n + 2) .

Система дифференциальных уравнений колебаний масс имеет матричный вид:

» »

M K U + D K U = 0

где U – вектор перемещений масс длиной K , D _K – матрица жесткости системы, M _K – матрица инерции, 'U — вектор ускорений. Если массы одинаковые, то матрица инерции пропорциональна единичной матрице M K = m I K . Элементы матрицы податливости B K , обратной к матрице жесткости D _K , в случае одинаковых жесткостей стержней вычисляются по формуле Максвелла-Мора:

b . = у s ⁽ i ) S ⁽ j l /( EF )                                    (2)

• i ,    j       / -J a a a

a = 1

где S^{_a i ) — усилие в стержне a от действия единичной силы в узле i, приложенной по направлению перемещения . Умножением уравнения (1) слева на матрицу податливости B _K задачу можно свести к проблеме собственных чисел матрицы B K : B K U = X U , где X = 1 / ( т ш ² ) — собственное число матрицы B K , ш — собственная частота колебаний. Здесь использовано тождество U = — ш ² U , справедливое для гармонических колебаний.

Формула для вычисления частоты колебаний имеет вид: ш = J 1 / ( m X ) .

Получить значения частот собственных колебаний для фермы с произвольным числом панелей в общем случае можно только в численной форме. Для этого можно использовать оператор Eigenvalues системы Maple.

Нижнюю границу первой частоты дает формула Донкерлея:

K

Ш — ² = Е ш — ²                                   (3)

i = 1

где ш — парциальная частота колебания массы т , расположенной в узле i . Известны другие варианты этой формулы [29,30]. При вычислении парциальных частот ш уравнение (1) имеет скалярную форму:

mH,. + du. = 0, i ii где ui - перемещение массы, ui- вектор ускорений, di - скалярный коэффициент жесткости (i — номер массы). Частота колебаний груза ш^ = ^di / т . Коэффициент жесткости, обратный коэффициенту податливости, определяется по формуле Максвелла – Мора:

n2

• *. = 1/ di = Е(SО') ) ‘a /(EFa )

a =1

Здесь обозначено S ^ i' ) — усилия в стержне с номером a от действия единичной силы, приложенной к узлу i . Из (3) и (4) следует:

K            к           K У ,22

ш — = m Е 7 = m Е « = m EE ( ^S . ) ) L / ( EF ) = m ( ^S . + S , +S. ).

i =1 d i         i =1              i =1 a =1

Для удобства вычисляются три отдельные суммы, соответствующие колебаниям по оси x , y и z . Величина S x , например, состоит из суммы отдельных прогибов по направлению оси x в узлах фермы от действия единичных сил, направленных по оси x . Аналогичный смысл имеют и два других слагаемых. Последовательный расчет S x в аналитической форме в системе Maple при различных n дает следующие значения:

n = 1: S x = (503 a ³ + 152 c ³ + 152 h ³) / (36 a²EF ), n = 2 : S x = (1751 a ³ + 846 c ³ + 1066 h ³) / (54 a²EF ), n = 3 : S x = (2065 a ³ + 1236 c ³ + 1676 h ³) / (36 a²EF ), n = 4 : S x = (799 a ³ + 542 c ³ + 762 h ³) / (9 a²EF ),...

В общем случае: S x = (C 1 x a ³ + C 2x c ³ + C 3x h ³) / (a ² EF ), где общие члены последовательностей коэффициентов в этих выражениях получаются обработкой решений для n =1,2,..,10 операторами системы:

C 1 x = (350 n ² + 943 n + 216) / 108,

C 2 x = n (11 + 65)/18,

C 3 x = n (305 n - 77) / 54.

Аналогично обобщение сумм S y для колебаний по оси у , рассчитанных для ферм различного порядка, дает решение S y = ( C 1 _v a ³ + C 2, c ³ + C 3, h ³ )/( a ² EF ), где:

C 1 y = (20 n ⁴ + 136 n ³ + 64 n ² + 87 n + 36) / 12,

C 2 y = n (15 n ³ + 12 n ² + 54 n + 31) / 6,

C 3 y = n (25 n ³ + 38 n + 49) / 6.

Обобщение сумм     S z    (колебания по вертикали) дает решение

S z = ( C 1 z a ³ + C ₂ z c ³ + C 3 z h ³) / (h ² EF ) с коэффициентами C 1 z = C ₂ z = n /6, C 3 z = 25 n /6 + 2.

В результате нижняя оценка для первой собственной частоты свободных колебаний фермы по методу Донкерлея принимает вид:

EF

V m (( C a ³ + C c ³ + C  h ³) / a ² + ( C a ³ + C c ³ + C h ³) / h ²),

1xy           2xy           3xy                      1z            2z           3z где

C 1 x _y = C 1 x + C 1 y = (90 n ⁴ + 612 n ³ + 463 n ² + 863 n + 270) / 54,

C 2 _xy = C 2 _x + C 2 _y = n (45 n ³ + 36 n ² + 227 n + 104) / 18,

C = C + C, = n (225 n ³ + 647 n + 364) / 54.

3 xy        3 x       3 y

• 3    Результаты и обсуждения / Results and Discussion

  3.1    Пример

Погрешность найденного приближенного аналитического решения можно оценить на примере. Зависимости частоты u D от числа панелей, вычисленной по формуле (5) и частоты u 1 , полученной численно, как минимальная частота всего спектра собственных частот конструкции при a = 3м , h = 5 м, представлены на рисунке 4. Масса грузов в узлах равна 400 кг. Модуль упругости стержней конструкции принят равным E = 2,1 • 10 ⁵ МПа, площадь поперечных сечений F = 36 см ² . С увеличением числа панелей первая частота u 1 собственных колебаний фермы, полученная численно, и оценка u D Донкерлея (5) сближаются. Зависимость относительной погрешности e D = | u D — u 1 | / u 1 от числа панелей приведена на рисунке 5.

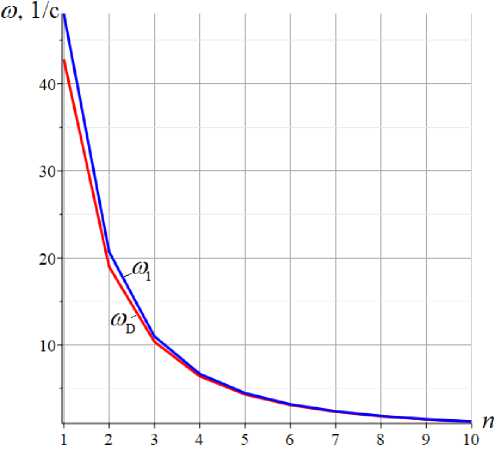
Рис. 4. – Первая частота колебаний, полученная двумя способами в зависимости от числа панелей

Fig. 4. – The first oscillation frequency obtained in two ways depending on the number of panels

В зависимости от числа панелей погрешность приближенного решения меняется от 13%, при n = 1 , до 2%. Степень приближения решения по Донкерлею несколько увеличивается при увеличении высоты конструкции.

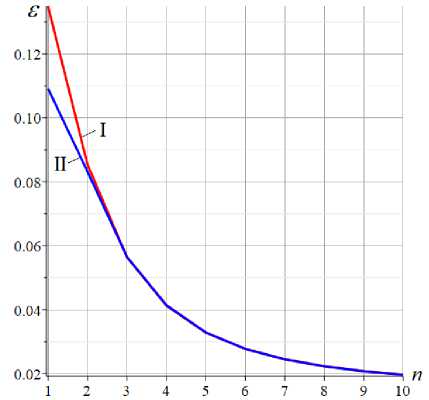
Рис. 5. – Относительная погрешность полученной оценки (5). I — h =3 м; II — h =5 м;

Fig. 5. – Relative error of the obtained estimate (5). I — h =3 m; II — h =5 m

По сравнению с известными решениями для оценки первой частоты колебаний стержневых конструкций, полученными по методу Донкерлея [7,19], решение (5) значительно более точное и сопоставимо по точности с верхней оценкой по методу Рэлея [31]. При большом числе панелей ( n >2) точность найденного решения практически не зависит от высоты конструкции.

3.2    Спектр частот регулярных ферм

На практике в динамических расчетах сооружений чаще всего используется первая собственная частота спектра, однако при анализе резонансных явлений в расчет берутся и более высокие частоты. Аналитический расчет этих величин в общем случае затруднителен. Анализ же распределения частот в спектрах семейства регулярных частот различного порядка выявляет некоторые характерные его особенности, позволяющие в некоторых случаях упростить расчет ферм высокого порядка [6].

На рисунке 6 приведены спектры собственных частот двенадцати ферм различного порядка, полученные численно.

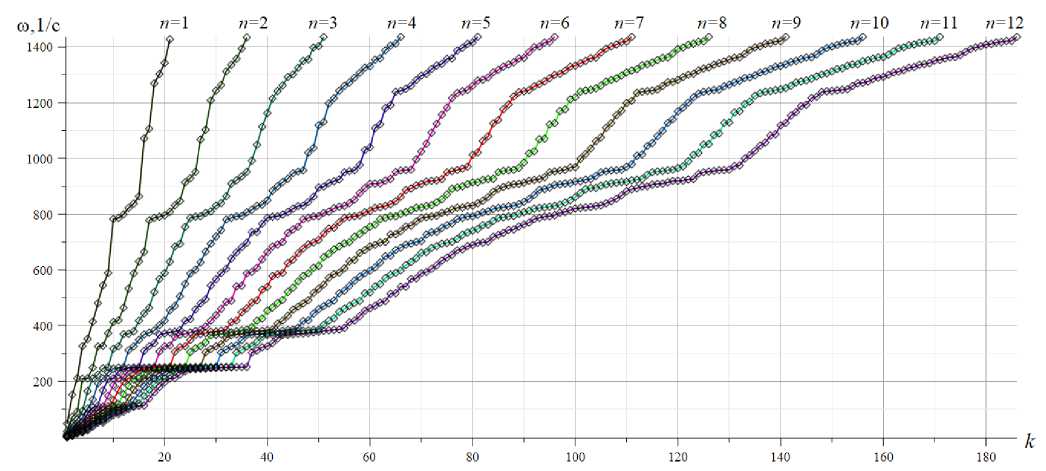
Рис. 6. – Спектры частот регулярных ферм, h =5 m

Fig. 6. – Frequency spectra of regular trusses, h =5 m

Частоты спектров отдельных ферм объединены условными кривыми. Ординаты точек на этих кривых — частоты, абсциссы — номера частот в соответствующем спектре. Например, спектр фермы с одной панелью ( n =1) содержит K = 3(5n + 2) = 21 частот, в спектре фермы порядка n = 12 содержится186 частот.

Распределение частот показывает, что независимо от порядка конструкции высшая частота колебаний ш остается почти постоянной: ш =1427.619, 1434.525,..., 1436.412, max                                         max

1436.412 1/c. Эта закономерность позволяет оценивать высшие частоты регулярной фермы с большим числом панелей. Расчеты собственных частот ферм большого порядка трудоемки и здесь наиболее вероятно накопление ошибок округления. Поэтому для верхней границы частот таких ферм с высокой степенью точности можно использовать значение высшей частоты, полученное для фермы первого порядка, величина которой следует из сравнительно простого расчета.

• 4    Заключение / Conclusions

Основные результаты работы:

• 1.    Предложена схема пространственной статически определимой регулярной фермы.

• 2.    Найдена аналитическая зависимость нижней границы первой частоты собственных колебаний от размеров фермы и числа панелей.

• 3.    В семействе спектров собственных частот ферм различного порядка обнаружено, что высшая частота колебаний не зависит от порядка конструкции.

• 5 Fundings / Финансирование

  Работа выполнена при финансовой поддержке РНФ 22-21-00473.