Аналитический способ задания областей теней зданий и сооружений с целью определения оптимального их места расположения на заданной местности

Известно, что продолжительность инсоляции, под которой понимается время облучения территорий застройки солнечными лучами, оказывает положительное психологическое и оздоровительное действие на человека. Под облучением понимается совокупность светового, биофизического и теплового воздействия. Поэтому при планировании места расположения жилых строительных сооружений на заданной местности необходимо учитывать положение почасовых теней в течение всего светового дня. В связи с этим продолжительность инсоляции нормируется и устанавливается для помещений жилых и общественных зданий. Требования норм инсоляции достигают соответствующим размещением и ориентацией зданий, а также их объемно-планировочными решениями. В работах [1–5] приведены геометрические методы определения положений теней зданий и время инсоляции в течение заданного интервала времени. Рассмотрим аналитический способ задания границ данных теней, которые могут быть использованы для автоматизированного расчета областей, характеризующих продолжительность инсоляции территорий застройки. Указанные области используют при размещении строительных жилых сооружений при различной их ориентации и заданном положении линейных объектов, в качестве которых выступают линии электропередач, трубопроводы, автомобильные и железные дороги.

На рис. 1, а изображены области почасовых теней Ai, построенные в различные моменты времени, заданные восемью, одиннадцатью и трина- дцатью часами, где параметр i определяет количество почасовых теней. Каждая отдельная область Ai может быть задана пересечением областей Xj (полуплоскостей), определяемых прямыми линиями. Область полуплоскости Xj в декартовой системе координат может быть задана с использованием неравенства [4]:

fi = ^-x 0 ( У / + 1 ^- У / ) ⁺ У 0 ( x i + 1 ^- x i ) ^-

• ^-Х + 1 У / ^{+ х} / У / + 1 >  0, ⁽¹⁾ где x_i , y_i и x_{i+ 1}, y_{i+ 1} – координаты точек A_i и A_{i+ 1} соответственно; x ₀, y ₀ – координаты текущей точки прямой. На рис. 1, а представлены две области X + и X - , которые расположены соответственно слева и справа от прямой, проходящей через точки A 1 и A 2 . Функция (1) положительная в открытой области Х | и располагается слева от вектора A A 2 , и отрицательная в открытой области X - , расположенной справа от него. Для задания области почасовой тени ∆ _i используем операцию пересечения областей:

• A , ^ (((( X 1 oX 2 ) о X з ) о Х 4 )Х 5 ) >  0, (2) где X j - полуплоскости определяемые неравенствами (1). Для здания, имеющего форму прямоугольной призмы, проекция тени отображается виде пятиугольника j = 5. Использование неравенства (2) позволяет определять принадлежность точек плоскости области A i и находить принадлежность точек областям почасовых теней. Для вычисления области A i заданной неравенством (2) используют операцию

  конъюнкции булевой алгебры, которую определяют следующим выражением [6, 7]:

  X 1 л X 2 = X 1 + X 2 — 7 X 12 + X 22 , (3) где X 1 и X 2 – являются аргументами R -функции, которые задают неравенствами (1). Подставляя вначале два неравенства (1) в уравнение (3), получают пересечение двух полуплоскостей образующих область X 1 nX ₂.

  Затем полученное неравенство области X 1 nX 2 и третье неравенство (1) подставляют вновь в уравнение (3) и получают уравнение области (( Х 1 n X 2 ) n X ₃). При этом получают пересечение трех областей. В результате использования всех пяти неравенств (1) получают в конечном итоге уравнение области A i . Для вывода уравнения контура области ∆ i заданного многоугольника, состоящего из n отрезков, воспользуемся следующими уравнениями. Уравнение, с помощью которого выделяется элемент из данного чертежа, имеет вид [6, 7]:

  q о (f, Ф ) = ^ f ² + Ф 2 — Ф = 0. (4)

  Для случая задания отрезка прямой М ₁ М ₂ значение параметра f этого уравнения определяется по формуле (1). Значение параметра ф уравнения (4) следующее [6, 7]:

  ^ф 4 [ ⁽ x 2 ^{— х} 1 ) ^{+ (} y 2 ^{— у} 1 ) ^—

  
  

  Пусть необходимо разместить строящиеся здания внутри области заданной многоугольником M_i (рис. 2). Указанный многоугольник M_i на рис. 2 изображен штриховой линией. Вершины данного многоугольника задают точки M ₁, M ₂ и т. п. Базовые точки сооружений обозначим O 1 , O 2 , O 3 и O 4 , а центры зон Ω 1 , …, и т. д. точками K 1 , K 2 , K 3 и K 4 . Точки O i определяют начала подвижных систем координат, в которых заданы объекты P_i и области Ω i . Зададим обобщенные координаты q 1 , …, q 8 , определяющие взаимное расположение объектов P i (положение объекта P 1 по отношению к неподвижной системе координат O_o x_o y_o задают параметры q ₁ и q ₂, объекта P ₂ по отношению к объекту P 1 – соответственно параметры q 3 и q 4 и т. п.). В этом случае обобщенные координаты q i определяют взаимное положение двух объектов друг относительно друга. Необходимо определить положение объектов P_i , при котором сумма ∑q_i = min принимает минимальное значение и при котором обеспечен максимальный уровень освещенности (при этом объекты P_i и области Ω _i не пересекаются между собой).

  При данном положении объектов P_i площадь, занимаемая ими, будет минимальна, и объекты не будут располагаться за пределами многоугольника M_i . Заметим, что многоугольник заданный точками M j , определяется линейными объектами. Примем

  
  
  

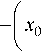
  ^х 2 ^{+ х} 1 ]

  2 )

  
  

  —

  
  

  y ₀

  
  

  У 2 ⁺ У 1 ]

  2    )

  
  

  > 0.

  
  
  
  

  Согласно формулам (4), (5) уравнение отрезка A 1 A 2 , соединяющего точки A 1 ( x 1 , y 1 ) и A 2 ( x 2 , y 2 ), может быть задано в виде:

  ^ (x,y^,x 1 ,у ,x 2 ,y 2 ) =

  
  

  ' x 0 ^{— Х} 1 ) ( У 2 ^— У 1 ) ^— ( У о ^— У 1 ) ( ^х 2 ^{— Х} 1 ) ] ^{2 +}

  
  
  
  

  1 l ²

  4 12

  
  

  x ₀

  
  

  Х 1 + Х 2 ]

  2 J

  
  

  2 1 ² ^ 2

  
  

  - 1/ 2 + I X

  4 ' 12 ⁺ 1 ^х 0

  
  

  —

  
  

  ^x 1 ^{+ x} 2

  
  
  
  
  
  

  ⁺ l ^y 0

  
  

  — У 1± У 2 ) = 0 , (6)

  
  

  где l₁₂ = ((х ₂ — х 1 ) ² + (у ₂ — у 1 ) ² - длина отрезка.

  Пользуясь уравнением (6) как стандартной формулой для отрезка, можем составить уравнение объединения произвольного числа отрезков по заданным координатам их концов задающих области ∆ i . Продолжительность инсоляции в течени-ие заданного интервала времени будут задавать области Ω _i , полученные пересечением областей ∆ _i . На рис. 1, б представлена область Ω _i , определяющая зону застройки, находящуюся в тени в течение трех часов в определенный интервал времени.

  
  
  

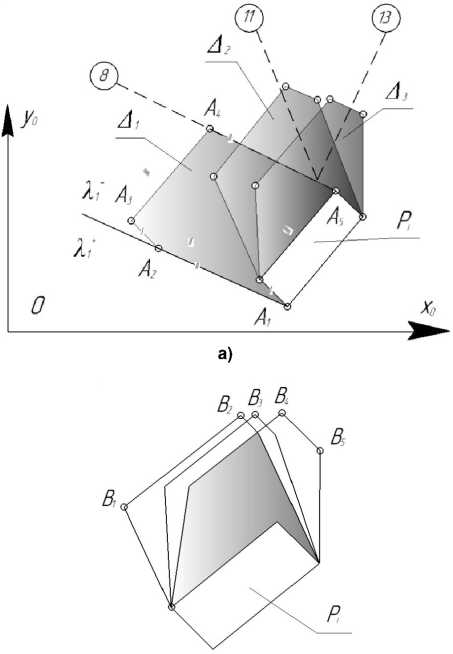
  б)

  Рис. 1. Задание областей теней: а – почасовые тени, б – область, расположенная в тени в течение трех часов

  
  
  

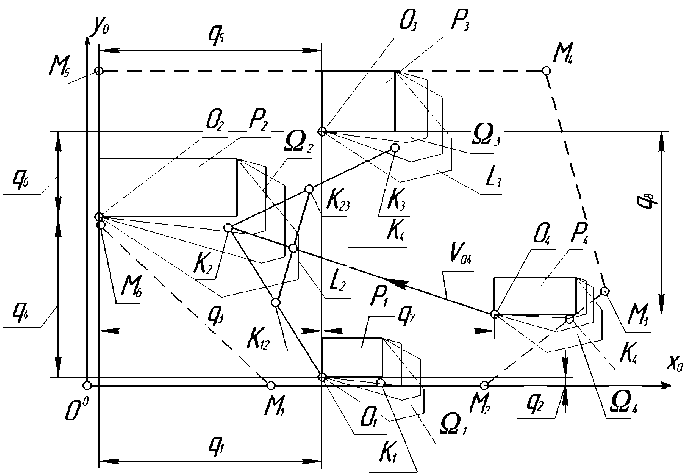
  Рис. 2. Параметры, характеризующие взаимное расположение объектов P i

  
  

вначале исходно заданные положения объектов P 1 ,…, P 4 на максимальном удалении друг от друга, при котором они касаются границы многоугольника M_i . Для данного положения объектов центры зон Ω _i на рисунке задают точки K ₁, K ₂, …, и K ₄. Данные точки вычисляют на основе нахождения центров диагоналей A_iA_{i+ 2}. Для указанного положения объектов P_i возможно определить границы зон теней fi i (1 - 6).

Если границы взаимно не пересекаются с объектом P i , то возможно уменьшение значений q i . Для уменьшения значений q i сместим объект P 4 в направлении целевой точки К ц , где отсутствуют изображения теней Ω i . Для этого определим вначале вспомогательные точки K 12 и K 23, располагающиеся на середине отрезков K ₁ K ₂ и K ₂ K ₃.

Далее вычислим целевую точку K _ц, которая находится на середине отрезка K ₁₂ K ₂₃ (см. рис. 2). Пусть необходимо определить положение объектов P_i при неизменной их ориентации. Тогда подвижную систему координат с центром в точке O ₄ и объект P 4 смещают в направлении целевой точки K ц в соответствии с вектором скорости V 04 , модуль которого определяют исходно заданной величиной m . Вектор смещения V 04 определяют компонентами ∆x 04 и ∆y 04 [8]. Смещение точки О 4 по направлению вектора V_{О 4} обеспечивают изменением значений обобщенных координат q_i . Для этого используют линейную систему уравнений:

J 11 a 11 9 1 +J 12 a 12 ^ 2 + — + J 18 a 18 ^ 8 =^A '04 ,

J21 a 2191 +J2 a 22^2 + — +J28 a 28^8 =Ay 04, (7) где 9i,92, —. , 98 — определяют скорости (или приращения ∆qi) обобщенных координат и вектор q (91, 92, —,98); a 11, a 12, —, a8 — значения весовых коэффициентов изменения обобщенных скоростей. При решении уравнений (10) необходимо использовать значения весовых коэффициентов аij. Где i=n, n – размерность вектора q, i=r, r – размерность вектора V04. Если направление вектора смещений VО4 не совпадает с направлениями смещений, при которых обобщенные координаты уменьшаются, то значения весовых коэффициентов изменяют на противоположное [8]. С помощью значений весовых коэффициентов также возможно отдавать предпочтение изменению той или иной обобщенной координаты qi. Предпочтение отдается последнему перемещаемому объекту. J11, J12, …. J24 – коэффициенты матрицы частных передаточных отношений [8]. При этом смещение объектов Pi будет аналогично смещению звеньев плоского механизма, имеющего восемь поступательных кинематических пар, движения в которых определяют обобщенные координаты qi [8].

Для однозначного решения линейной системы (7) используют критерий минимизации объема движения [8].

in^qi = min. (8) i= 1

Решение линейной системы уравнений (7) при выполнении условия (8) позволяет определить вектор q_M (q₁... 9 8 ). Новое положение объектов P i и областей теней Ω i находят изменением обобщенных координат (при этом принимаем допущение Aq i » i ):

q i = q i + ^ q i . (9)

Далее необходимо найти новые положения объектов Р i , а также областей Ω i и определить их взаимное расположение. Таким образом, осуществляют малые движения объектов Р_i до тех пор, пока области Ω _i и Р_i не начнут пересекаться между собой. При возникновении данной ситуации век-

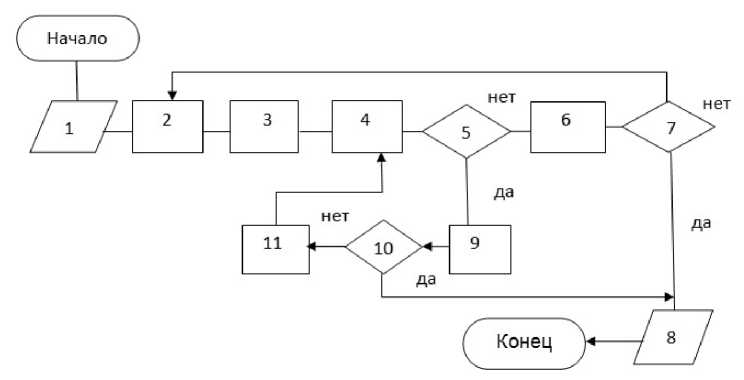
Рис. 3. Схема алгоритма смещения объектов P i , позволяющая минимизировать занимаемую площадь застройки

тор приращений обобщенных координат в этом случа е опре дел яю т по з а висим ос ти [8]:

∆qn = qм + ∑ k _i m _i Qp ,                (10)

i= 1

где q_м – вектор оп ред ел ё н ный в с оотв етс тви и с условиями (8), k i – коо рдинаты точки N р -плоскости Г , о п ре де ляем ой л и н ей н ой с ист емой (7); Qp – ед инич ные н а пра в ляющ ие векторы, за да ющие напра в л ени я ос е й ре пе ра с в яз а н ного с р -пл ос кость ю (2). Д л я опреде л ени я не обх о ди м ого см е ще ния, пр и котором в ы пол н яе тся усл овие не пересечения областей Ω _i и Р_i , п ере би рают зна чения параметров k ₁, …, k_l , где l = 6. После определения положения объекта Р ₄ ( ког да точк а O ₄ достигнет целевой точки K _ц ) и с пол ьзу ют син те з д вижений объекта Р ₃ с из м е не н ие м те пе рь ше с т и о б обще н ных коорди на т в н а пра в л ени и новой целевой точки К ц . В этом с лу ча е объ е кт Р 4 остается не под в и ж ным . Дл я оп ред е л е н ия н ов ого пол о жени я цел е в ой т очки и спол ь з уют в с пом ога тел ьные точки К 12 (на середине отрезка К 1 К 2 ) и К 24 (на середине отрезка К 2 К 4 ) при этом К 12 К ц = К ц К 24 . Схема ал гори тм а с и нте з а д в и ж ени й объ е кто в Р_i с целью о п ре де л е н ия их по л ож е н ия , п ри котором д ан ные о б ъ е кты з а н им а ют м и н им а льн у ю пл ощадь, и м акси ма л ь ный у ров е нь ос в е щеннос т и пре дс та вл ена на рис. 3. При минимальных з на чен и ях обоб ще н ны х координат пл ощадь з ан им а е м а я объ е кта м и Р_i будет минимальна.

Н а рис . 3 приняты сл е д у ю щие обоз на че н ия: 1 – ввод исходных данных q i , m, t max , массивов M i , P i , Ω i и K i , задающих размеры и ф о р м у о бъе к т о в P i , областей Ω i и координат точек K i в системах координат O 1 ,…, O 4 , с в я з ан ны х с объе к там и P i ; 2 – вычисление координат точек K ₁₂ , K ₂₃, K _ц, вектора V ₀₄ ( ∆x ₀₄ ,∆y ₀₄) и значений а_i j ; 3 – вычисление компонентов вектора q_м (7, 8); 4 – вычисление положений объектов P_i и областей Ω _i в с оо т в етстви и с (2) ; 5 – о п р ед еле ни е ус ло в и я п е р есеч ения о б л астей P_i и

Ω _i , и областей P_i с многоугольником M_i (1–6); 6 – изменение обобщенных координат q_i (9); 7 – целевая точка достигнута; 8 – вывод значений обобщённых координат, задающих конечное положение объектов P_i ; 9 – t = t + 1; 10 – значения t > t _max (где t – номер итерации, t max – максимально заданное число итераций); 11 – вычисление вектора qn (10).

Результаты вычислительного эксперимента, связанного с одним из этапов моделирования смещения объектов Р i , с использованием зависимостей (1 - 10) представлены на рис. 4. Моделирование движения выполнено в системе САПР ACAD с использованием алгоритмического языка программирования AutoLISP [9]. На рисунке отрезки О _о О _о1, О _о1 О ₁, О ₁ О ₁₂, О ₁₂ О ₂, О ₂ О ₂₃, О ₂₃ О ₃, О ₃ О ₃₄ и О ₃₄ О ₄ задают длины, определяющие начальные значения обобщенных координат q_i .

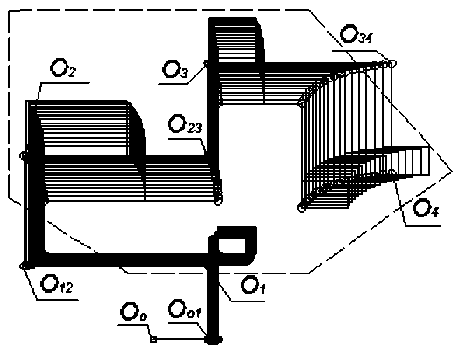
Рис. 4. Результаты моделирования одного из этапов синтеза перемещения объектов Р i

Заключение

Результаты моделирования синтеза малых перемещений строящихся сооружений с целью размещения их с обеспечением максимального уровня освещенности разработанным способом показали необходимость использования значений весовых коэффициентов, задающих изменения приращений обобщенных координат. Значения весовых коэффициентов рационально задавать в зависимости от удаления центров областей Ωi от целевой точки Kц, а также от направления вектора смещений и направления векторов q1,… при которых значения обобщенных координат уменьшаются. Разработанный способ определения места расположения зданий с учетом минимизации занимаемой ими площади и обеспечения максимального уровня их освещенности может быть использован при составлении планов территорий застройки различными жилыми сооружениями на заданной местности.