Аналитическое и компьютерное моделирование поверхностей методом криволинейного проецирования

Конструктивные способы образования поверхностей создавались в разные времена и соответствовали потребностям науки и техники [1, 2]. Первым из них был кинематический метод, который появился вместе с возникновением начертательной геометрии [3]. На стадии зарождения этот метод был применён для формообразования линейчатых поверхностей. Первой вехой в развитии этого метода явилось отнесение одной из инцидентных линий в бесконечность. В классе линейчатых поверхностей был выделен подкласс линейчатых поверхностей с плоскостью параллелизма – поверхностей Каталана 1 . Следующим конструктивным способом образования поверхностей следует признать способ преобразований, появление которого связано с зарождением научной специальности «Прикладная геометрия, ин-

• ¹    Hazewinkel Michiel , ed. (2001). Catalan surface, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4.

женерная графика». Первыми шагами использования способа преобразований стали применения аффинных и гомологических преобразований сложных поверхностей в более простые с целью упрощения решения задач начертательной геометрии [4].

Дальнейшее развитие прикладной геометрии поверхностей ассоциировалось с решением в основном методологических проблем: теории определителя поверхности [5], теории каркаса [6], теории параметризации [7]. Способ изъятия линейного каркаса поверхности с множественного числа, в частности с конгруэнции линий, следует из этих теорий. Одним из распространённых способов выделения линейного каркаса поверхности с конгруэнции является погружение в неё линии. Кроме конгруэнции прямых в формообразовании поверхностей применяются конгруэнции окружностей, парабол [8], плоских кривых [9], цилиндрических винтовых линий, конических винтовых линий [10].

Вопросам формообразования оболочек посвящено большое количество работ. Геометрические исследования формообразования оболочек в архитектуре обобщены в [11]. До середины ХХ века точный аналитический метод расчёта циклических оболочек был заменён приближённым расчётом относительно простых систем, на которые можно было расчленить конструкцию. Инженеры, механики и архитекторы, используя только приближённые методы расчёта, создали немало конструкций и сооружений в форме циклических поверхностей. Из циклических поверхностей широко известны и используются: поверхности вращения, круговые винтовые поверхности и трубчатые поверхности с произвольной плоской линией центров. В циклических поверхностях одно семейство образующих кривых представляет собой окружности постоянного или переменного радиуса, что значительно упрощает процесс изготовления тонких оболочек в форме этих поверхностей.

Аналитическому описанию циклических поверхностей, в т.ч. поверхностей Иоахимста-ля 2 , с использованием различных подходов посвящено много работ [12, 13]. Конструктивная схема формообразования поверхности Иоахимсталя заключается в отыскании поверхности, несущей на себе траектории, ортогональные к семейству сфер с центрами на прямой [14].

1    Постановка задачи и методы

В работе использованы приёмы формообразования оболочек из циклических поверхностей Иоахимсталя. Аналитическим методом исследована система проецирования сплошной конгруэнцией окружностей с общей радикальной осью, любая проецирующая поверхность которой – циклическая поверхность Иоахимсталя.

Пучком окружностей на плоскости называют множество окружностей 1 , имеющих общую радикальную ось. В зависимости от количества общих точек, имеющих окружности пучка с радикальной осью, пучки могут быть: гиперболические (нет общих точек), параболические (одна общая точка) и эллиптические (две общие точки). Пучки окружностей с центрами на осях OX и OZ , радикальными осями которых являются соответственно оси OZ и ОХ , называют сопряжёнными. Параметрич еские уравнения семьи окружностей имеют вид:

x = ( a - —) + ₃ ( a - — ) 2 - a ² + r ² cos t ,

2 u 2 u (1)

z = ₃/( a - —)² - a ² + r ² sin t ,

2u где a – абсциссы центра, r – радиус любой окружности, u – параметр пучка. В кинематическом способе формообразования поверхностей функции x = f (t, u, v), y = фt, u, v), z = v(t, u, v) выражают связь между прямоугольными декартовыми координатами x, y, z и специальной параметризацией пространства с помощью параметров u, v, которые являются криволинейными координатами на поверхности-носителе, и параметра положения t поверхности-носителя в его движении. Вращением вокруг оси OZ пучка (1) можно прийти к конгруэнции окружностей, параметрические уравнения которой:

1. ,          1              2 . 2.

x = a --+ _Л ( a --) - a + r cos t cos v , 2 u V2 u

1 L 1          7     7. .

y = a --+ , ( a --) - a ² + r cos t sin v ,

• 2    u } 2 u

• 1    -.2        2 ,2 • x

z = .. ( a --) - a + r sin t .

V 2 u

Поскольку пучок окружностей (1) симметричен относительно оси OZ , вращать для получения конгруэнции следует не весь пучок, а его часть, расположенную в полуплоскости. Конгруэнцию (2) окружностей с общей радикальной осью называют сплошной.

Если вращать вокруг общей радикальной оси пучок окружностей вместе с сопряжённым пучком, первый описывает конгруэнцию траекторий, ортогональных к семейству сфер, образованных вращением сопряжённого пучка. Таким образом, чтобы получить параметрические уравнения циклической поверхности Иоахимсталя, необходимо воспользоваться уравнениями, выражающими поверхность как множество лучей конгруэнции ортогональных траекторий, которые проецируют линию:

x = f ( w ), y = ф w ), z = V ( w ) . ⁽³⁾

Линию следует выбрать на одной из сфер, образованной вращением окружности сопряжённого пучка. В результате получается уравнение поверхности, как семьи окружностей конгруэнции (2), проецирующих точки линии (3):

( а ( w ) + 7 ( в ( w ) - d ) ² + V ² ( w )( V ² ( w ) + 2 ( в ( w ) + d )) cos t ) f ( w ) ^{2 e (} w )

У =

(a( w) + 7 (в( w) - d )2 + V2 (w)(V2 (w) + 2( в( w) + d)) cos t )ф( w) 2e(w)                          ’ z = где f (w) = a cos(w0 + c sin(wn ))cos w, ф( w) = a cos(w0 + c sin(wn ))sin w,

V ( w ) = a sin( w ₀ + c sin( wn )) + r ,

-^ ( в ( w ) - d ) ² + v ² ( w )( v ² ( w ) + 2 ( в ( w ) + d )) sin t

² 7 ^{e (} w )

a ( w ) = 2 a ( a + r sin( w ₀ + c sin( wn ))), в ( w ) = a ² cos ² ( w ₀ + c sin( wn )),

,      2      2

d = a - r

• а, r - соответственно расстояние от радикальной оси центра и радиус окружности, что вместе с радикальной осью задаёт пучок окружностей, который в результате вращения образует конгруэнцию окружностей;

• r, a - соответственно расстояние от начала координат на радикальной оси и радиус сферы инциденции сферической линии;

• w₀ - широта начальной параллели, которая является криволинейной осью синусоидальной сферической линии, аналога оси абсцисс плоской синусоидальной кривой;

• c - криволинейная амплитуда синусоидальной сферической линии - аналог амплитуды плоской синусоидальной кривой;

n - количество складок (целое);

w - криволинейная координата на сфере сопряжённого пучка.

При любых выражениях функций (3) уравнения (4) выражают циклическую поверхность Иоахимсталя. Уравнения (4) удобны тем, что координатные линии t = const , w = const - это линии кривизны. На такое совпадение ориентированы методы расчёта оболочек [15, 16].

Особый интерес представляет выявление влияния параметров, входящих в уравнение (4), на форму оболочки. Окружность радиуса r с координатами центра (а, 0) на плоскости ZOX задаёт вместе с осью OZ первоначальный пучок окружностей с общей радикальной осью OZ. Окружность радиуса а с координатами центра (0, r) задаёт в плоскости ZOX пучок, сопряжённый с первоначальным пучком. Вращением вокруг OZ сопряжённый пучок образует семью сфер с центрами на OZ, а первоначальный пучок - конгруэнцию окружностей, которые являются ортогональными траекториями семьи сфер (рисунки 1-3). Следовательно, параметры а и r напрямую и отдельно друг от друга влияния на форму поверхности Иоахимсталя не имеют. Влияние имеет их соединение, а именно a2 - r2 = d.                                                 (5)

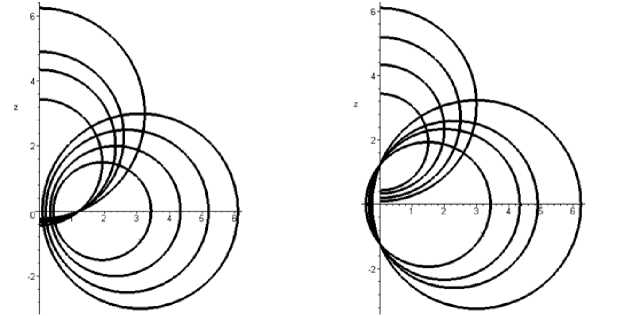
Рисунок 1 - Первичный гиперболический и сопряженный эллиптический пучки окружностей

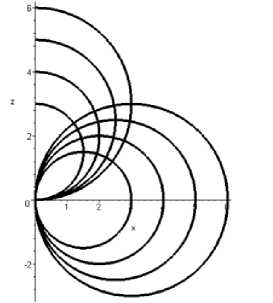
Рисунок 3 - Первичный и сопряжённый параболические пучки окружностей

Рисунок 2 - Первичный эллиптический и сопряжённый гиперболический пучки окружностей

2    Результаты

При исследовании влияния параметров а и r на форму поверхности Иоахимсталя выявлено три возможных случая:

Случай 1. a > r ( d >0 ). Первоначальный пучок окружностей - гиперболический, сопряжённый - эллиптический (рисунок 1).

Гиперболический пучок окружностей содержит окружность нулевого радиуса, то есть при r = 0, a = dd. В этом случае сопряжённый пучок окружностей эллиптический. Все окружности сопряжённого пучка проходят через две фиксированные точки: M1(a, 0), M2 (-a, 0). В результате вращения вокруг оси OZ точка М1 описывает окружность радиуса a с центром в начале координат. Через него проходят все сферы, образованные вращением окружностей сопряжённого пучка. С целью установления достоверности результата относительно правильности параметрических уравнений (4), необходимо показать, что окружность x2 + у2 = a2, z = 0                                  (6)

удовлетворяет уравнению (4) при r = 0 .

Из уравнения (4) при условии z = 0 следует: sin t = 0 , что было обусловлено ранее, когда назначалось начало отсчёта параметра t ; равенство нулю подкоренного выражения:

( a ² cos ² а - a ² ) ² + a ² sin ² a ( a ² sin ² a + 2 a ² cos ² a + 2 a ² ) = 4 a ⁴ sin ² a = 0 ,       (7)

где a = w ₀ + c sin( wn ).

Равенство (7) возможно в двух случаях: a = 0 или sin a = 0 . Сопоставив, получится w ₀ = 0 , c = 0. Поскольку w о и с использованы в представлении сферической линии на одной из сфер пучка, образованного сопряжённым пучком окружностей, то подставив полученные значения r = 0 , sin t = 0 , cos t = ± 1 в уравнения (4), получится:

x =

2 a ³ cos w

2 a

, У =

2 a ³ sin w

2 a ²

z = 0 .

Если возвести обе части последних равенств (8) в квадрат и приравнять суммы левых и правых частей полученных равенств, получится выражение:

x ² + y ² + z ² = a ² .                                      (9)

• (9)    – уравнение сферы, которое при z = 0 переходит в уравнения (6) линии пересечения сферы плоскостью z = 0.

Таким образом, при r = 0, z = 0, w0 = 0, c = 0 получается сферическая линия - окруж- ность (6), которую нельзя использовать для представления поверхности (4), поскольку лучи конгруэнции, образованные первоначальным пучком, есть окружности нулевого радиуса.

Случай 2. a < r ( d <0 ). Первоначальный пучок окружностей – эллиптический (рисунок 2), все его окружности проходят через две фиксированные точки, расположенные на оси OZ : N ₁ ( 0 , 7 r ² - a ² ), N ₂ ( 0 , - 7 r ² - a ² ).

Точки N 1 , N 2 являются фокальными для конгруэнции ортогональных траекторий семьи сфер, образованной сопряжённым пучком окружностей. Любая поверхность конгруэнции проходит через эти точки. Значение параметра t для н их:

22 r - a , _ t = ± arcsin--+ n r . (10)

В этом случае необходимо принимать во внимание уравнение, показывающее равенство нулю радиуса сферы, которая принадлежит пучку, образованному сопряжённым пучком окружностей.

Случай 3. a = r ( d = 0 ). Первоначальный и сопряжённый пучки окружностей – параболические (рисунок 3).

Окружности первоначального пучка и образованной им конгруэнции соприкасаются с радикальной осью OZ. Окружности сопряжённого пучка соприкасаются с радикальной осью OX, а образованные ими сферы семьи с центрами на OZ соприкасаются с плоскостью XOY. Как первые, так и вторые касания происходят в начале координат, который можно рассмат- ривать как вырождение окружности конгруэнции – геометрического места окружности нулевого радиуса первоначального пучка при его вращении вокруг OZ в момент перехода гиперболического первоначального пучка в параболический.

Т.к. а и r входят в определитель как первоначального, так и сопряжённого пучков окружности, которые в свою очередь образуют соответственно конгруэнцию ортогональных траекторий и семью сфер, непосредственно окружность радиуса r с центром (a, 0) и сфера радиуса а с центром (0, r) могут быть вне области определения создаваемой поверхности Иоахимсталя. Такое же заключение можно сделать в отношении сферической линии, которая задаётся функциями f (w), ф(w), ^(w) на сфере радиуса а с координатами центра (0, r). Область определения поверхности зависит от интервала значений t, который определяется в процессе построения.

При d < 0 и интервале t поверхность будет иметь две конические точки N 1 ( 0 , 7 r ² - a ² ) и

N 2 ( 0 , - T r ²

7 π

- a2 ) . Рисунок 4 демонстрирует такой случай при 0 < t < — . Построения по- верхностей производились с помощью программы Maple.

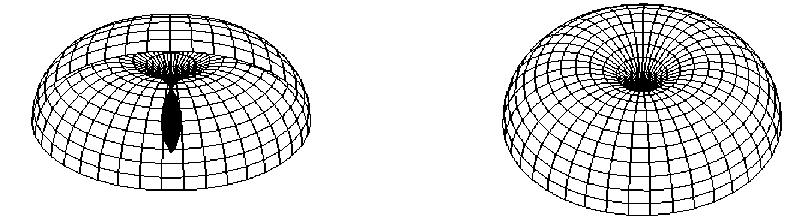
Рисунок 4 – При d < 0 и интервале 0 ≤ t ≤ π поверхность имеет две конические точки 6

N 1 ( 0 , 7 r ² - a ² ) и N 2 (0, - 7 r ² - a ² )

Добиться исключения отсека, расположенного между коническими точками, можно 5π уменьшением интервала до 0 ≤ t ≤ (рисунок 5).

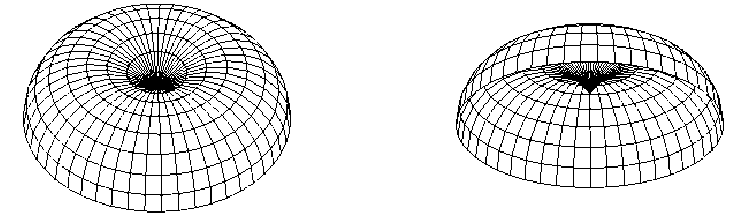
Рисунок 5 – При d < 0 уменьшение интервала до 0 _≤ t _≤ 5 π для исключения отсека, 6

расположенного между коническими точками

Пределу интервала отвечает одна коническая

π точка. Дальнейшее уменьшение интервала 0 ≤ t ≤ приводит к появлению отверстия (рисунок 6).

Следует отметить, что касательные в точках N 1 , N 2 к семье линий w = const , по которым поверхность (4) пересекается с плоскостями пучка и с осью OZ , образуют конусы (рисунок 7). При d = 0 точки N 1 и N 2 совпадают друг с другом и с началом координат. Окружности w = const не пересекаются с осью OZ , а

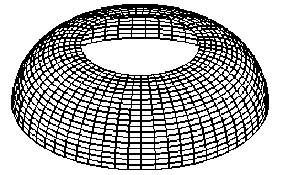
Рисунок 6 – Появление отверстия при уменьшении интервала до 0 _≤ t _≤ π 2

соприкасаются с ней в начале координат. Конус касательных к линиям w = const поверхности (4) вырождается в прямую линию – ось OZ . Особой точке (начало координат) поверхности

(4) отвечает значение t = π (рисунок 7).

Поскольку наличие такой острой формы в конструкциях крайне нежелательно, для предотвращения её появления рекомендовано назначать соответствующую границу интервала таким образом, чтобы интервал не содержал t = п . Если ограничиться значениями 0 <  t <  2 п (исключая t = п ), то верхней границе интервала t = п определения поверхности соответствует её направленность остриём вниз, нижней границе – остриём вверх (рисунок 8).

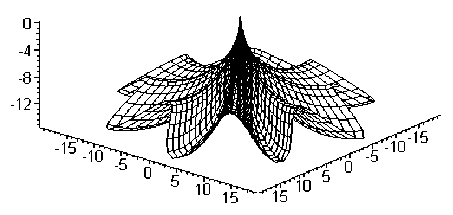
Рисунок 7 – Особая точка (начало координат) поверхности (4) при d = 0, которой соответствует значение t = п

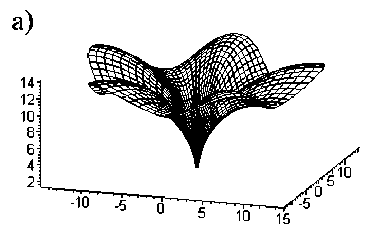
Рисунок 8 - Положение острия поверхности (остриё вниз при t <  п , остриё вверх при t > п ): а) при 1 , 5 <  t <  3 ; б) при 3,5 <  t <  5

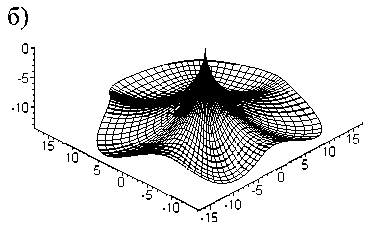
Конгруэнция окружностей, образованная первоначальным пучком, имеет плоскость симметрии XOY . Поэтому смена знака параметра w 0 на противоположный не влияет на положение и направление острой формы (рисунок 9) в особой точке (начале координат).

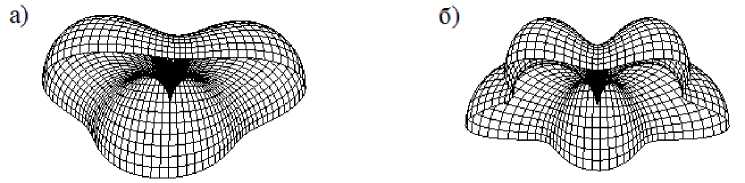
Рисунок 9 – Форма поверхности при смене знака параметра w 0 : а) при

п wn = - -; б) при w0 = - w0    4          0   4

Параметр w 0 влияет на величину проекции амплитуды с на ось OZ . На рисунке 10 наглядно показано влияние изменения параметра с на получаемые модели поверхности. Амплитуда сферической синусоидальной линии – это её экстремальное отклонение вдоль меридиана сферы от окружности с широтой w 0 .

На форму поверхности также влияет параметр n , который соответствует количеству складок. При n = 1 получается дважды циклическая поверхность Иоахимсталя – отсек цик-лиды Дюпена (рисунок 11а), при n = 2 поверхность напоминает шляпу (рисунок 11б), при n > 2 – появляются хорошо выраженные складки, количество которых равно n .

Необходимо подчеркнуть, что семьи координатных линий w = const (окружности или их дуги) и t = const (сферические линии) являются линиями кривизны. Соединение (совпадение) координатной сетки с сеткой линий кривизны важно при использовании методов расчёта оболочек.

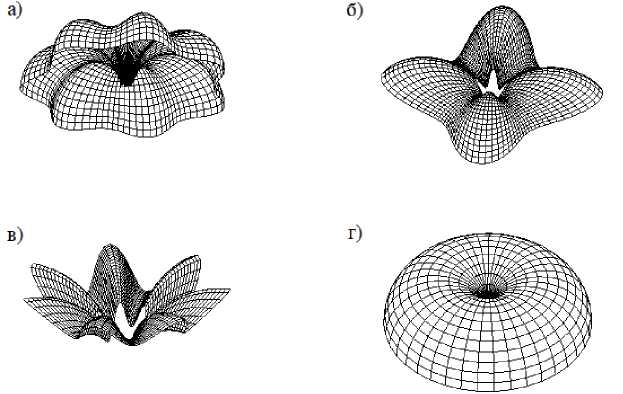
Рисунок 10 – Модели поверхности при разных значениях параметра с : а) с = 0,07; б) с = 0,15; в) с = 0,2; г) при с = 0 получается поверхность вращения

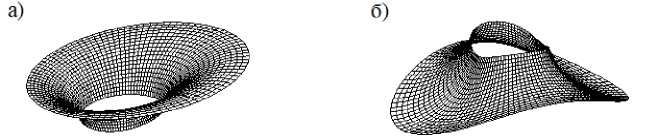
Рисунок 11 – Поверхности при разных значениях параметра n , который соответствует количеству складок: а) при n = 1 получается дважды циклическая поверхность Иоахимсталя – отсек циклиды Дюпена;

б) при n = 2 поверхность напоминает шляпу

3    Выводы

По результатам анализа исследований, проведённых в области образования поверхностей лучами криволинейного проецирования, можно сделать следующие выводы.

На примерах показаны широкие возможности формообразования циклических поверхностей Иоахимсталя, которые рекомендованы для использования в проектировании складчатых оболочек, благодаря следующим свойствам:

• ■    многопараметричность общих моделей, позволяющая охватить широкий круг форм варьированием значениями параметров;

• ■    отнесение к линиям кривизны, что является предпосылкой применения методов расчёта оболочки на прочность;

• ■    программные реализации разработанных аналитических моделей позволяют оценить конструктивные и эстетические качества оболочки по наглядным графическим изображениям.

Применение методов криволинейного проецирования и поверхностей, образуемых этими методами, охватывают различные области [17-24]: решение задач начертательной геометрии, профилирование режущего инструмента, конструирование исполнительных органов землеобрабатывающих машин, моделирование пространства на плоскости, конструирование оболочек. Системы проецирования рассматриваются не только на плоскости, но и на криволинейных поверхностях.

Полученные поверхности и их алгебраические описания можно использовать для разработки удобных для работы плагинов различных программных комплексов (рисунки 12-16), в том числе для программ геометрического 3D моделирования и BIM программ (Компас 3D, Nanocad, Inventor, Renga, Revit и др.), а также для разработки расчётных моделей объектов не только для получения геометрии, но и при формирования сетки (Meshing) расчётных моделей (программы Ansys, ЛИРА САПР, Scad и др.) [25-27].

Рисунок 12 – Винтовая нарезка трапецеидальной резьбы

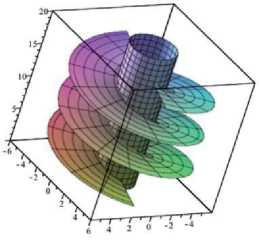
Рисунок 13 – Визуализация поверхности «Шнек»

Рисунок 14 – Модель шнека для бу- Рисунок 15 – Модель компрес-рения                             сора

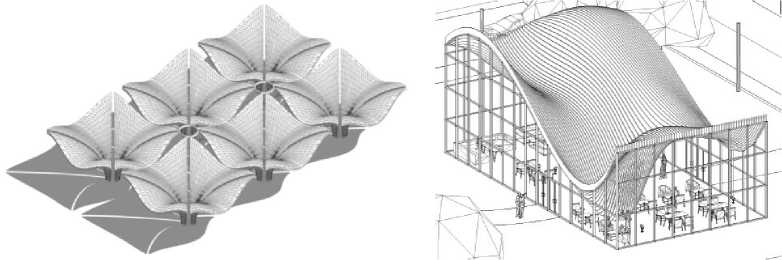
Рисунок 16 – Модели навесов

Заключение

Применение систем криволинейного проецирования в научных исследованиях, проектировании и производстве на оборудовании с числовым программным управлением сдерживается отсутствием общей математической модели, на основе которой можно было бы разрабатывать и развивать необходимые компьютерные технологии. Такая ситуация вызвана тем, что способы криволинейного проецирования зарождались и развивались на конструктивной основе, их аналитические интерпретации были разрознены и не привели к возникновению схемы обобщённого характера. Решения основывались на алгебраическом подходе, в то время как современные программные продукты в этой области ориентированы на параметрическое представление.

Общая аналитическая модель, предложенная в работе, реализована для систем криволинейного проецирования, лучами которых являются окружности. Циклические поверхности могут принимать привлекательные с точки зрения архитектора формы. Поэтому важно иметь теоретическое обобщение поставленной задачи, которое представлено в разработке общей аналитической модели систем криволинейного проецирования и их проецирующих поверхностей, отличающихся параметрическим представлением, которое позволяет выделить ха- рактерную семью линий на поверхности в системах компьютерной графики и затем в системах с числовым программным управлением программировать обработку вдоль этих линий. На параметрическое представление ориентированы современные пакеты автоматизированных систем научных исследований, автоматизации проектных работ и технологической подготовки производства.