Аналитическое описание потока протонов кольцевого тока Земли для питч-угла 90 градусов

Земной кольцевой ток - это электрический ток, текущий к западу вокруг Земли, обычно располагается на расстояниях между ^ 2 и 9 Re (Re - средний радиус Земли). Его источник, рост и спад сильно связаны с геомагнитными бурями. Захваченные энергичные (~ десятки кэВ) положительные ионы ( Н +, Н е + и О+) подвергаются азимутальному дрейфу и составляют кольцевой ток бури. Три первичных процесса, находят ответственными за. спад кольцевого тока: процессы кулоновских столкновений и обмена, зарядами вместе с питч-угловой диффузией электромагнитными иоппо-циклотроппыми волнами [1].

Недавно были выполнены численные исследования по динамике во время бури энергичных частиц радиационных поясов и также для частиц кольцевого тока. Земли, так как их потоки находят сильно изменяющимися. Такая сильная вариация динамики радиационных поясов и кольцевого тока. Земли рассматривается как вклад от взаимодействий волна-частица, и от дрейфового резонанса, связанного с усиленными ультра, низкочастотными волнами. Однако одновременное наблюдение и соответствующее моделирование питч-углового рассеяния протонов кольцевого тока, электромагнитными ионно-циклотронными волнами во время магнитоспокойного периода ( Кр <  3) было сообщено редко [2]. Поэтому это первичная цель этого исследования.

1.    Математическая модель

Одномерное модифицированное уравнение Фоккера-Планка (или уравнение питч-угловой диффузии) для плотности фазового пространства, описывающее только "чистую" питч-угловую диффузию с потерями от взаимодействий волна-частица, может быть выражено [3, 4]

д/ dt

1__д_ sin а да

( sin а • D аа    - да

sin² а cos а dL

2L    dtt

-

-^ + S_± sin² а • /.

^T wp

Здесь / - плотность фазового пространства (или функция распределения), t - время, L - параметр МакИлвейна, а - локальный питч-угол от 0 до 180 градусов, D_aa - коэффициент питч-угловой диффузии [3, 4], ^dL )dt" радиальная скорость [3, 4], T_wp - время жизни вследствие взаимодействий волна-частица [3, 4], S e - перпендикулярный коэффициепт функции источника частиц (а = 90°) [3, 4].

Уравнение (1) - это оригинальная модель в пространстве скоростей, которая содержит некоторые математические модели питч-угловой диффузии как частные случаи, например [5 - 7].

Используя (1), как новая математическая модель предлагается обыкновенное дифференциальное уравнение для аналитического описания перпендикулярного дифференциального потока, заряженных частиц ( а = 90°) в магнитосфере Земли, которое зависит от времени и нескольких параметров:

Ф + / L dL +    7_± - 7 _± q   V =0

dt       2L dt   7±q (7±о + 2) Twp 7±    ’ гДе jx - перпендикулярный дифференциальный поток заряженных частиц j = 2mE J, т - масса заряженных частиц, E - энергия частиц), 7x0 - хорошо известиый (когда j = jx sin7 а)) показатель питч-углового распределения заряженных частиц (или индекс анизотропии питч-углового распределения), ио берется для питч-угла 90° при t = 0, 7x - средний показатель питч-углового распределения заряженных частиц на интервале времени вычисления (предполагается, что 7x ~ const).

Вывод уравнения (2) представлен в аппендиксе.

При определенных геофизических условиях и на. временном интервале приблизительно не более чем три часа (когда индекс геомагнитной активности Кр = const) или на большем временном интервале, когда Кр « const, уравнение (2) может быть решено аналитически.

Тогда, аналитическое решение уравнения (2) есть

^2 ^L 3 ^cosф      7_± — 7x0

^{j±( )   j±0} xp V ( 7948800    7xo (7x0 + 2) T_w) ) '                  '

Здесь jxo - перпендикулярный дифференциальиый поток заряженных частиц при t = 0. ф₂ в [8]. а ф - азимутальный угол (местное время LT = 0 ч в полночь) или геомагнитная восточная долгота в плоскости магнитного экватора.

Вывод уравнения (3) представлен в аппендиксе.

2.    Экспериментальные данные и расчеты

Дальше будет использовано коррелированное наблюдение усиленных электромагнитных ионно-циклотронных воли и динамической эволюции потока, протонов кольцевого тока, собранное спутником Cluster около положения L = 4,5 в течение 26 - 27 марта 2003 г. в магнитоспокойный период ( D_st > -10 нТл) [2]. Показано, что потоки энергичных (5 - 30 кэВ) протонов находят спадающими быстро (например, за. полчаса) для маленьких питч-углов, соответствуя активностям интенсивных электромагнитных ионно-циклотронных воли.

Для расчета мы должны взять следующие данные [2]: jxo(t =0 с) = 5, 5894 • 105 (см² с стер кэВ)^-1. j_x (t = 1800 с) = 2,1073 • 105 (см² с стсц> кэВ)^-1. Кр = 2.66 или 3 -. L = 4.17. ф = МLT = 22.58 ч. 7_Х0 = 0.5157. 7_Х = 0.5801. E = 17.1 кэВ. Затем используя (3) находим T_w = 91.4988 с и зависимость jx от t на. интервале t = (0 - 1800) с (Рис. 1).

Проведено сравнение результатов по предложенной модели (2) или (3) и по полной модели (1) для области питч-углов от 0 до 180 градусов. Получено для перпендикулярного дифференциального потока, протонов кольцевого тока. Земли очень хорошее согласие с максимальной относительной ошибкой приблизительно 3,23 %.

Заключение

Как математическая модель предлагается обыкновенное дифференциальное уравнение для аналитического описания перпендикулярного дифференциального потока, заряженных частиц в магнитосфере Земли, которое зависит от времени и нескольких параметров.

Модель позволяет также оценивать для разных геофизических условий время жизни вследствие взаимодействий волна-частица.

Получено в рассмотренном примере для перпендикулярного дифференциального потока, протонов кольцевого тока. Земли очень хорошее согласие с максимальной относительной ошибкой приблизительно 3,23 %.

Аппендикс

Вывод уравнений (2) и (3).

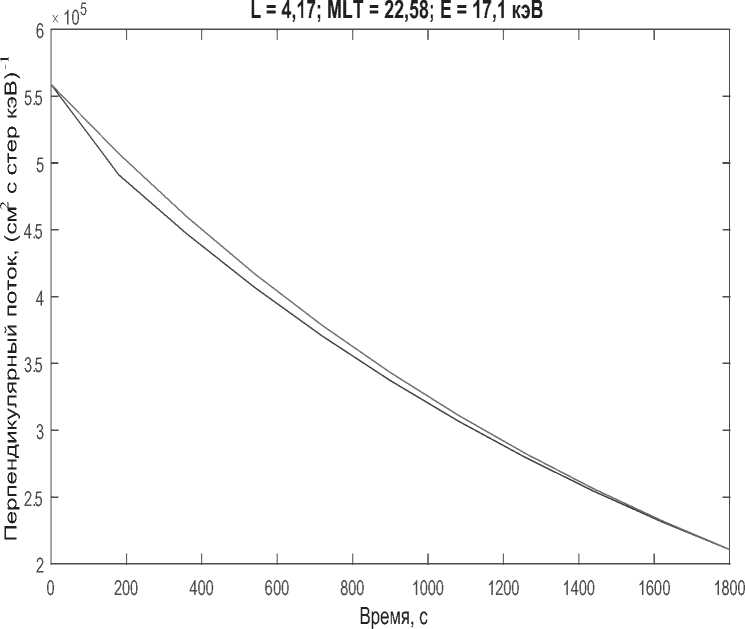
Рис. 1. Дифференциальные потоки протонов для питч-угла 90° по полной модели (1) - нижняя (синяя) линия и по предложенной модели (2) или (3) - верхняя (красная) линия.

Учитывая, что j = 2mEJ, т = const, Е = const и коэффициент питч-угловой диффузии предлагается определять [3, 4] следующим образом

D_act = D ^ sin² a =--------- sin² a,                       (Al)

7до (7до + 2) Тшр сначала из (1) получаем уравнение dj 1 д                   dj sin2 a cos a AL j ai = ™да (™aD-sl" aaaй^ё1) - 2^ + S±“ a^-    Ш|

Затем берем производные и в итоге получаем

И =^D_±^sin2^a£2 ^+sinacosa (3^D_± - J,^⁾ M ⁺

+ (— (2 cos² a — sin² a) A- ^^ —  + S± sin² a) j. 2 L do      L uj jj

При a = 90° и dL |± = о уравнение (АЗ) упрощается dj 1 _dia _ n d2j ,     ( 1 AL 1 Q \

Ai^|д = IT = ^D± aa2^{|д +} (2L di ^— T^_p^+Sr) ^j±.                ^(A4)

Исходя из зависимости j = j^ sin7 a, 7 = const = 7д можно доказать [7], что д2? , д02 |Д = —7±J±.                                    (Аб)

Тогда, используя [3, 4]

S = _(7±о+_³^

Д   (7до + 2) Twp и (А1), (А4), (А5), получается уравнение (2) = (Аб):

dn dt	1 dL + — 2L dt	+ T1-- S ^ + D-L7±) j± = 0,
dj. dt	/  1 dL + — 2L dt	+ 770 (to        ) j“ = 0-	(A6)

Чтобы получить уравнение (3), возьмем следующее приближенное равенство [3, 4], используя баупс-усредненную радиальную дрейфовую скорость движения заряженных частиц (измеренную в [1/с]) в магнитосфере Земли dL    /dL\       '’2,4     ,      2тт^2Ь4 cosф

(А7)

ht ~ \ "dt" / = -^ф0)Ь COSф = — 24 • 60 • 60 • 92’ где ф - азимутальный угол (местное время LT = 0 часов в полночь) или геомагнитная восточная долгота в плоскости магнитного экватора, П - угловая скорость вращения Земли, фо = 92 кВ, а зависимость ф2 (измеренная в [кВ]) от геомагнитной активности, т.е. от Кр- индекса, определяется по формуле [8]

'                                _            0,045

• ²    = (1 - 0,16Кр + 0, 01Кр²)³ "

Полагая все параметры в уравнении (Аб) постоянными (или приблизительно постоянными), находим точное (или приближенное) аналитическое решение уравнения (Аб) = (2) в виде (А8) = (3):

N2L3 cosф      7± - 7±о

³^ ^{) J±0} xp ( ( 7948800    7±о (7±о + 2) T_WJ ) ^-                " "