Аналитическое планирование ресурса мультисервисного узла на основе модели Эрланга, slicing и HAC/SAC-контроля

Расчет пропускной способности мульти-сервисных узлов при одновременной подаче голосовых, видео- и IoT-потоков остается сложной задачей. Существующие методы часто упрощают модель или требуют громоздкого моделирования [1-4]. Классические формулы Эрланга не учитывают современные технологии Slicing и Admission Control, а последние исследования либо ограничены узкими сценариями, либо не включают все необходимые параметры [5-7].

В данной работе мультисервисный узел представлен как многоклассовая система потерь Эрланга с параметрами статической и динамической доли трафика и глобальным порогом. Доказано сохранение мультипликативной структуры вероятностей, что позволяет создать эффективный рекурсивный алгоритм для произвольного числа классов [8]. Аналитически сравниваются четыре варианта Slicing и контроля доступа, выявляя оптимальные условия для минимизации блокировок, что дополняет существующие экспери- ментальные данные строгой теоретической оценкой [1-3, 8].

Аналитическая оценка показателей качества мультисервисного узла

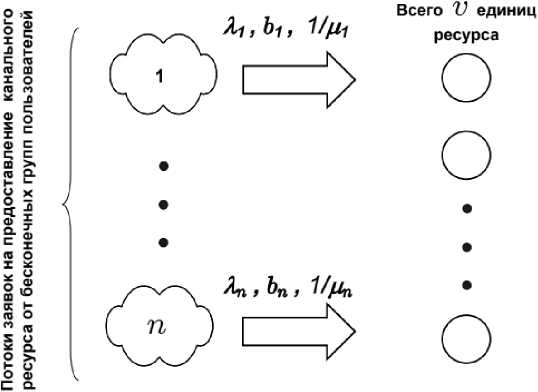
Рассмотрим мультисервисный узел как многоклассовую систему потерь Эрланга, в которой п пуассоновских потоков заявок с экспоненциальным временем обслуживания конкурируют за общий ресурс емкостью v каналов.

Модель поступления и обслуживания заявок k-го потока, к = 1,..., п:

• -    поступление заявок подчиняется закону Пуассона с интенсивностью Л_к ;

• -    время обслуживания заявки распределено экспоненциально со средним 1/^ к ;

• -    для обслуживания заявки требуется Ь к единиц ресурса;

• -    заявка принимается к обслуживанию, если i₁b₁ + — + i_nb_n + Ь_к< v.

Динамику совместного обслуживания заявок опишем непрерывным марковским процессом:

Характеристика поступления заявок

Передаточный      Отличительные ресурс узла доступа свойства в канальных единицах

Тип трафика

• Сервисы реального времени

Тип модели

• Мультисервисный аналог модели Эрланга

Область использования

• Расчёт пропускной способности мультисервисных линий концентрации абонентского трафика

Рис. 1. Схема мультисервисной модели Эрланга

• -    Пространство состояний. Достаточность ресурса узла доступа оцениваем долей потерянных заявок, а эффективность его использования - средним числом занятых единиц ресурса. Для оценки этих характеристик достаточно знать долю времени пребывания узла в состоянии с известным числом заявок каждого потока, находящихся на обслуживании. Выбор характеристик определяет состояние модели в виде вектора (i₁, .., i_n), где i k -число обслуживаемых заявок к-го потока. Значения i k ограничены пропускной способностью узла X n= ₁ i k b_k ^ и. Векторы (i₁,.,i_n), удовлетворяющие приведенному неравенству, определяют пространство S состояний модели.

• -    Марковский процесс. Динамика изменения состояний модели во времени описывается случайным процессом r(t) = (i i ⁽t) .^,i n ⁽t)), где i k ⁽t) - число заявок к-го потока, находящихся в момент t на обслуживании. Процесс r(t) будет марковским, поскольку построен в соответствии с положением конструктивного определения марковского процесса, т. е. можно показать, что время пребывания r(t) в любом (i₁,.,i_n) ES распределено экспоненциально с известным параметром и далее с известными вероятностями

происходит переход r(t) в другие состояния из S.

• -    Границы вспомогательных множеств состояний. Обозначим через U k множество состояний (i₁,.,i_n)ES, удовлетворяющих условию i₁b₁ + —+ i_nb_n + b k > v. В каждом из состояний множества U k поступившая заявка к-го потока получает отказ. Пусть S i Q S - множество состояний таких, что i₁b₁ + ^ + i_nb_n = i. В каждом из состояний множества S i занято i единиц ресурса.

Для оценки функционирования узла введем ключевые показатели качества - вероятность отказа каждого класса и среднюю занятость ресурса, рассчитываемые через стационарные вероятности состояний модели.

• -    Обозначим через p(i₁,.,i_n) стационарную вероятность состояния (i₁,.,i_n). Она имеет интерпретацию доли времени пребывания r(t) в (i₁,.,i_n). Это свойство позволяет использовать p(i₁,.,i_n) для оценки характеристик модели.

• -    Качество обслуживания заявок к-го потока определим долей потерянных заявок ^ k . Для вычисления ^ k воспользуемся свойством PASTA, которое позволяет оценить n_k с помощью выражения:

- Загрузку ресурса обслуживанием заявок к-го потока оценим средним числом занятых канальных единиц т_к . По определению:

т к = S_(i1..... ы&Р^-Л п ) i k Ь к

• -    Обозначим через Z k средний битрейт узла, используемый на обслуживание заявок к- го потока. По определению Z k = т к с, где с -скорость передачи, обеспечиваемая одним каналом.

• -    Обозначим через У к среднее число заявок к-го потока, находящихся на обслуживании. Справедливо соотношение У к = т к /Ь к .

• -    Для доказательства существования стационарных вероятностей и возможности их использования для оценки введенных характеристик необходимо составить и решить си-

• стему уравнений равновесия, связывающую значения p(i1,..., in).

Стационарное распределение состояний задается системой уравнений равновесия, формулировку и интерпретацию которой приведем ниже.

• -    Система уравнений равновесия (СУР). Для доказательства существования стационарных вероятностей р(х) марковского процесса r(t) и их оценки необходимо решить СУР следующего вида:

Р⁽х)а_х = E (y)es\{ _X } Р ⁽У) ^ у Р у, _х = Е (у)Е5\{х} Р(У⁾^ у, _х,     (х) Е S    (3)

Параметры а_х, а у^ , У ^ х полностью задают СУР и находятся в процессе реализации конструктивного определения марковского процесса:

ах - сумма параметров экспоненциальных распределений случайных величин, совместно определяющих время пребывания модели в (х);

а у, _х - параметр экспоненциального распределения времени до наступления события, определяющего переход r(t) из (у) в (х).

Запись СУР исследуемой модели узла доступа одним соотношением:

P(i 1..... ^Т £=1 (Л к^ + Ь к <ъ^ к^

= % п=1 Р (ii.....1 к -1, ■ , i n ) Л к Шк > 0)                           (4)

+ Ъ П=1 Р&.Л)(1 к + 1)Р_к1(1 + Ь_к<г)

где (1 1 ,..., 1 П ) Е S, значение i = i₁b₁ + —+ i_nb_n представляет из себя ресурс, занятый в состоянии (i₁,.,i_n), а /(•) - индикаторная функция события. Она отсеивает несуществующие состояния и события, которые не приводят к требуемым изменениям состояния. Вероятности P(i₁,..., i_n) нормируются.

Ниже изложена пошаговая рекурсивная схема, позволяющая без перебора состояний вычислить стационарные вероятности и производные показатели качества.

Обозначим через P(i) - вероятность того, что всеми заявками в узле доступа занято i каналов.

• 1.    Положим значение Р(0) = 1.

• 2.    Выразим значения P(i) через Р(0) используя соотношение.

• 3.    Находим величину нормировочной константы:

• 4.    Определяем нормированные значения вероятностей p(i)

• 5.    Находим величины п_к и т_к для каждого из п потоков:

P⁽i) =¹Х к=1 ^ к Ь k P(i-Ь k ⁾                    (5)

и последовательно увеличивая i от 1 до V. При фиксированном i значения P(i — Ь_к~), к = 1,2,.,п либо уже представлены через Р(0)

(для i — Ь к >  0), либо равны 0 (для i — Ь к <  0). Рекурсия реализуется для всех i.

N = % = ₀P(i)

p(t)=™,    i = 0,1.....v                  (7)

^ к = E i= _v -b_k+1 P⁽ⁱ⁾,

Методы нарезки и ограничения доступа

Введем некоторые обозначения:

• а_к - статическая доля общего ресурса С, зарезервированная за к-м классом трафика;

• a k (t) — соответствующая динамическая

квота, которую контроллер может изменять во времени;

ft (0 < ^ < 1) - глобальный порог относительной занятости ресурса, при достижении которого активируется механизм HAC/SAC.

Если в квоте а к С нет свободных блоков, заявка блокируется, даже если в других сегментах есть ресурсы. Это обеспечивает стабильность для чувствительных к задержкам приложений.

Динамическая нарезка регулирует ак(Ь) в зависимости от нагрузки, позволяя перераспределять ресурсы между классами. При этом сохраняется защита приоритетного трафика, что усложняет аналитическую оценку стацио- тк = акьк(1 — Лк), к = 1,..., п. (8)

В мультисервисных узлах ресурсы распределяются не случайно, а с помощью нарезки (Slicing), разделяющей общий ресурс на сегменты для разных классов трафика. В статическом варианте класс к получает квоту а к С, и при поступлении заявки проверяются условия:

'£ j=₁bj i j < С (9)

• Y j ₌₁b j i j + Ь_к< а_к С (10)

нарного распределения p(i), так как оно зависит не только от суммарной загрузки. На практике часто используют приближенные методы, предполагая быстрое усреднение аМ

Admission Control ограничивает прием новых заявок при высокой загрузке. Жесткий контроль (HAC) блокирует заявку класса к, если:

X j= ₁ b_t i j + Ь_к > ft С

Это сохраняет стабильность уже обслуживаемых вызовов. Мягкий контроль (SAC) допускает новые заявки, снижая пропускную способность всех активных потоков.

Иногда часть ресурса Лк резервируется под критичные приложения, снижая вероятность отказа для класса к, но уменьшая доступный ресурс для остальных:

С

-

^Л к

к

В динамических сценариях нарезка сочетается с HAC/SAC: ак(Ь) растет с нагрузкой, но глобальный порог ft С ограничивает перегруз- ку. В марковской модели это исключает недопустимые состояния, и нормирующая сумма для стационарных вероятностей становится:

G(C) = Х_т -.Ж ьт<с ^{п (m)}> П(т) = Пы^, P k = ^    ⁽¹²⁾

^J—1 ^{J J                                           m} k ‘                f^k

Такая модель ограничивает глубокую перегрузку, перераспределяя блокировки в пользу приоритетных классов. Выбор параметров ^a k (t) P, Лк обычно основан на моделировании и тестах, поскольку аналитический поиск оптимума сложен. Далее анализируется сочетание статической и динамической нарезки с разными Admission Control и их влияние на вероятности отказа для различных типов трафика.

Анализ характеристик статистической и динамической нарезки

В условиях фиксированного распределения ресурсов каждый класс трафика ограничен своей статической квотой, что обеспечивает предсказуемость и гарантии обслуживания, особенно для приоритетных потоков. Однако такая жесткая нарезка приводит к неэффективному использованию пропускной способности, поскольку свободные ресурсы одного сегмента остаются недоступными для других, что вызывает избыточные блокировки при пиковых нагрузках. В марковской модели это выражается в запрете состояний, где занятость класса превышает выделенную долю, даже если общий ресурс не исчерпан. В результате при низкой нагрузке одного класса наблюдается недозагрузка сети, а вероятность отказа возникает не только из-за переполнения, но и из-за ограничений внутри «среза» класса.

Динамическая нарезка предлагает более гибкий подход, позволяя перераспределять неиспользуемые ресурсы между классами в зависимости от текущей нагрузки. Такой механизм учитывает баланс между потоками и временно увеличивает квоты для перегруженных категорий, что отражается в изменении множества достижимых состояний и переходов в марковской модели. Однако это усложняет аналитическое описание, поскольку вероятность блокировки перестает зависеть только от суммарной загрузки, и часто приходится прибегать к аппроксимациям с усредненными значениями квот. Динамическая схема эффективнее при переменных и трудно прогнозируемых нагрузках, снижая простой ресурсов и перераспределяя пропускную способность, но может повышать риск задержек у приоритетных классов без дополнительных механизмов резервирования и контроля.

Сравнение этих подходов показывает, что статическая нарезка обеспечивает стабильность и простоту управления, что важно для мультимедийных сервисов с жесткими требованиями к качеству, тогда как динамическая нарезка лучше подходит для сценариев с интенсивным и разнообразным IoT-трафиком, где важна адаптивность. Полностью гибкие модели, пересматривающие квоты в реальном времени, требуют сложных процедур контроля и часто сочетаются с механизмами ограничения доступа для предотвращения перегрузок. Выбор оптимальной стратегии обычно основывается на имитационном моделировании и анализе конкретных условий эксплуатации, учитывая компромисс между эффективностью использования ресурсов и гарантированным качеством обслуживания.

Система видеоконференцсвязи

В системах видеоконференцсвязи методы нарезки и ограничения доступа играют ключевую роль в управлении ресурсами мульти-сервисных узлов. Статическая нарезка обеспечивает предсказуемое распределение полосы, закрепляя фиксированные доли за каждым классом трафика, что упрощает контроль приоритетов и гарантирует стабильное качество для критичных сервисов. Однако при значительной неравномерности нагрузки часть ресурсов может простаивать, что снижает общую эффективность и увеличивает вероятность отказов в перегруженных сегментах. Динамическая нарезка, напротив, позволяет гибко перераспределять неиспользуемые блоки в пользу активных потоков, что особенно важно при резких скачках трафика, например, в потоковом видео или массовой загрузке данных. При этом без дополнительных механизмов резервирования и жестких порогов ограничения существует риск ухудшения качества обслуживания для других важных приложений.

Влияние методов нарезки на потери заявок тесно связано с применяемыми механизмами Admission Control. Жесткое ограничение препятствует превышению заданного порога загрузки, сохраняя качество приоритетных сес- сий, но может приводить к излишним блокировкам, которые можно было бы избежать при временном перераспределении ресурсов. Мягкий контроль допускает новые подключения даже при высокой загрузке, перераспределяя пропускную способность между всеми активными потоками, что иногда повышает суммарную пропускную способность, но увеличивает задержки для трафика с жесткими требованиями. В системах с интенсивным IoT-трафиком динамическая нарезка особенно эффективна, поскольку короткие транзакции быстро занимают освободившиеся блоки, а крупные мультимедийные потоки выигрывают от временного приоритета в «окнах» доступной полосы. Выбор оптимальной стратегии зависит не только от средней нагрузки, но и от ее суточных колебаний и характера трафика, что требует комплексного анализа и моделирования для каждой конкретной системы.

Заключение

В работе предложена целостная аналитическая схема для расчета пропускной способности мультисервисного узла доступа. Узел описан как многоклассовая система потерь Эрланга, в которую введены параметры статической и динамической «нарезки» ресурса (ak, а^О и глобальный порог загрузки ft, отражающие практику slicing и HAC/SAC- контроля в SDN/5G-сетях. Доказано, что при таких ограничениях стационарные вероятности сохраняют мультипликативную форму, благодаря чему получена компактная система уравнений равновесия.

На этой основе разработан линейный рекурсивный алгоритм, вычисляющий вероятности отказа и среднюю загрузку без перебора экспоненциально растущего пространства состояний; типичный расчет для v ~ 1000 каналов выполняется за миллисекунды. Аналитическое сравнение четырех связок «стати-ческая/динамическая нарезка × жест-кий/мягкий Admission Control» показало, что динамический slicing в паре с SAC повышает утилизацию канала до ≈ 95 %, тогда как статическая схема с HAC минимизирует блокировки приоритетного трафика.

Полученная методика дает операторам связи быстрый инструмент точного планирования ресурса, снижая как CAPEX (за счет отказа от избыточных резервов), так и OPEX (благодаря автоматическому подбору ^_k(t) и ft). Перспективой дальнейших исследований являются ML-процедуры, которые будут он-лайн-обучать динамические квоты и пороги, а также расширение модели на сценарии с непуассоновскими потоками и коррелированными временами обслуживания.