Аналитическое решение динамических уравнений движения твердого тела с жидкостью большой вязкости

За последние несколько десятилетий вновь актуальной стала задача исследования движения твердых тел и их систем с жидким наполнением. Основным источником таких задач является проблема движения летательных, в том числе космических, аппаратов, содержащих существенный запас жидкого топлива. Зачастую масса топлива составляет большую (а иногда преобладающую) часть массы всей системы, что говорит о существенном влиянии жидких компонент на движение всей системы. Влияние оказывают следующие факторы: инертность жидкого топлива, вовле-каемость в движение (вращение), трение жидкости о стенки полости, колебания (всплески) жидкости при наличии свободных поверхностей.

Задаче исследования движения относительно неподвижной точки твердых тел с полостями, заполненными жидкостью, посвящено существенное количество работ [1-6]. Первооткрывателем в этой области является Н. Е. Жуковский [1]. Им получены первые математические модели систем с идеальной жидкостью. Далее подобными задачами занимались Б. Н. Румянцев [2, 3], Н. Н. Моисеев [3], Ф. Л. Черноусько [4, 5], А. Ю. Ишлинский [6]. Подавляющее большинство работ направлено на построение уравнений движения, включая решение гидродинамической задачи, или посвящено исследованию устойчивости конкретных (в основном, вращательных) движений. Имеется ряд публикаций, посвященных исследованию течений вязкой жидкости, например, [7, 8].

Гораздо меньше работ посвящено получению аналитических зависимостей параметров движения (координат и скоростей) систем от времени, начальных условий и инерционно-массовых характеристик системы. Объективной причиной этому является сложность механической системы твердого тела с жидкостью — она фактически является системой с бесконечным числом степеней свободы и требует применения аппарата дифференциальных уравнений в частных производных, который далеко не всегда (особенно в случае уравнения Навье — Стокса) позволяет получить аналитические решения. Возникает необходимость преобразовывать математические модели, чтобы они становились конечномерными. Больших результатов в этом добился Ф. Л. Черноусько [5].

В данной работе приводится математическая модель движения твердого тела с жидкостью большой вязкости и для частного случая получается аналитическое решение, которое для проверки правильности результата сравнивается с численным решением исходных уравнений.

1 Математическая модель

Согласно методике, предложенной Ф. Л. Черноусько [5], и в соответствии с логикой, представленной в [9], динамические уравнения движения относительно неподвижной точки твердого тела со сферической полостью, целиком заполненной жидкостью большой вязкости, в связанной системе координат (оси являются главными осями инерции) примут вид:

Ap) + (C - B)qr = Mx - pv 1D(A 1 [Mx + (B - C)(qr + qr)] +

+ qC 1 [Mz +(A - B) pq]- rB 1 [My + (C - A) pr ]);

Bq + (A - C) pr = My - pv1D (B1 [My + (C - A)(pr + pi*)] +

+ rA1 [Mx +(B - C) qr]- pC1 [Mz + (A - B)pq]);

Ci* + (B - A)pq = Mz - pv1D(C1 [A*z + (A - B)(pq + pq)] + + pB' [My + (C - A) pr]- qA' [Mx +(B - C)qr]), где A, B, C — моменты инерции твердого тела относительно главных осей x, y, z; p, q, r  — проекции вектора угловой скорости;

M x , M y , M_z — проекции главного момента внешних сил, p — плотность жидкости, v — кинематическая вязкость жидкости, D — параметр полости [5].

Рассмотрим случай, когда тело является динамически симметричным A = B , на него не действует внешний момент. Кроме того, величина pv ¹ D = s является малой из-за большой вязкости жидкости, что позволяет при отмеченных ограничениях пренебречь членами второго порядка малости. Тогда уравнения (1) преобразуются:

Ap + (C - A) qr = s( C - A) CA ' pr2;

,\q + ( A - C ) qr = s ( C - A ) CA ' qr ² ;                (2 )

Ci* = s ( A - C ) A ^{- 1} ( p ² + q ² ) r .

Умножим первое уравнение системы (2) на Ap , второе — на Aq , третье — на Cr .

A ² pp + A ( C - A ) pqr = s ( C - A ) CA - p ² r ² ;

< A2qq + A(A - C)pqr = s(C - A)CA-1 q2r2;

C ² i*r = s ( A - C ) CA ^{- 1} ( p ² + q ² ) r ² .

Сложим уравнения системы (3):

Проинтегрировав последнее выражение, получим первый интеграл уравнений движения (2):

A2 p2 + A2 q2 + C2 r2 = K2,(5)

где K = const .

2 Аналитическое решение динамических уравнений движения Введем замену переменных:

p = x cos y , q = x sin y , r = z .                   i

Тогда уравнения (2) примут вид:

A ( x cos y - xy sin y ) + ( C - A ) xz sin y = £ ( C - A ) CA

² xz ² cos y ;

< A ( x sin y + xy cos y ) + ( A - C ) xz cos y = £ ( C - A ) CA

² xz ² sin y ;

Cz = £ ( A - C ) A - ¹ zx ².

Выражая из системы (7) старшие производные введенных координат, получим:

5c = £ ( C - A ) CA - 3 xz ;

< y = (C - A)A

- ¹ z ;

Z = £(A - C)A-1C -1 zx2, где x и z — это медленные переменные типа «амплитуда», а y — быстрая переменная типа «фаза». Подставим замену переменных (6) в первый интеграл (5) и выразим:

x 2 = K ²

—

22 Cz

A ²

.

Подставим (9) в третье уравнение системы (8):

Z = £

( A - C ) zK 2

AC

—

22 Cz

A ²

.

Решая уравнение (10), получим:

K exp

z =

' £A - C)K21

к

1 + C ² exp 2

A 3 C

к

+ C 1

.

к

к

£ ( A - C ) K ² 1 A 3 C

^{+ C} 1

7 7

Переменная x выражается из (9):

x =

AK

1 + C ² exp 2

к к

£(A C )K 2 t + C )

A 3 C        ¹ JJ

.

После подстановки выражения (11) во второе уравнение (8) решим его относительно переменной y :

y = -

A ²

— ln l C exp ⁽ F ⁽ t ^{)) +} 7¹ + C exp ^{( 2 (} F ^{( t )))}1

£K L к                               7

+ C 2

,

£ A - C)K^t где F(t)=     nJ---+ C1.

A 3 C

Параметры K , C ₁ , C ₂ являются постоянными интегрирования и находятся из начальных условий:

p ^{( o )} = p o , q ^{( o )} = q o , r ^{( o )} = r o ;

x o = 7 p o ² + q o ², y o = arctg — , z o = r o ;

p ₀

к = 7 A ² p 2 + A ² q 2 + C ^{2 r} o ² .

Для того чтобы получить явные зависимости от времени компонент угловой скорости p , q , r тела в связанной системе координат необходимо подставить выражения (11), (12) и (13) в (6).

• 3 Верификация решений

Зачастую дифференциальные уравнения движения систем твердых тел с жидким наполнением не имеют точного аналитического решения. Такие системы исследуются численными методами. При этом получающиеся решения считают достаточно точными. Сравним аналитические решения, полученные в предыдущем пункте, с решением системы (2), полученным численно. На рисунках 1–3 показаны результаты численного (кривая 1) и аналитического (кривая 2) расчетов.

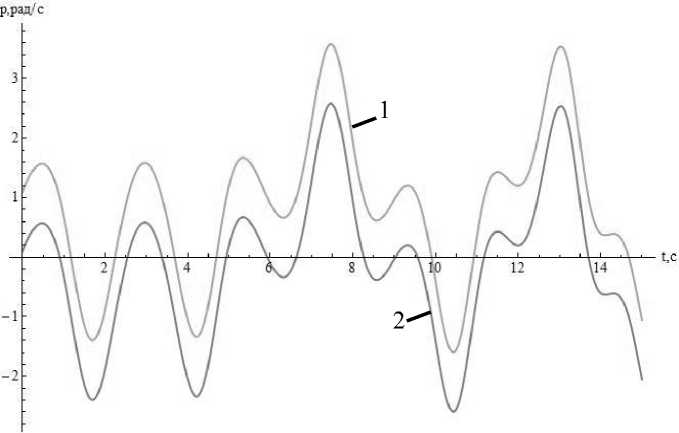
Рис. 1. Зависимость проекции угловой скорости p от времени: 1 — численное решение; 2 — аналитическое решение.

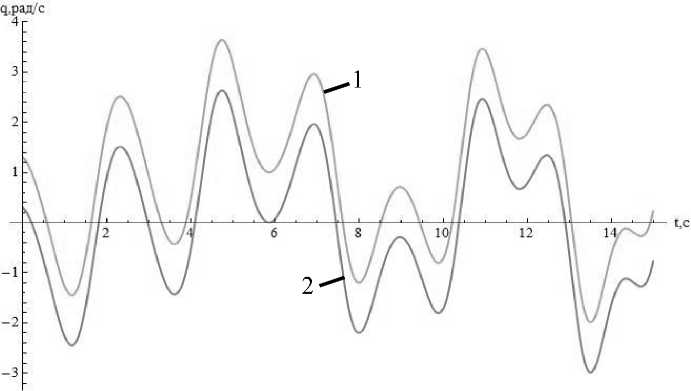
Рис. 2. Зависимость проекции угловой скорости q от времени: 1 — численное решение; 2 — аналитическое решение.

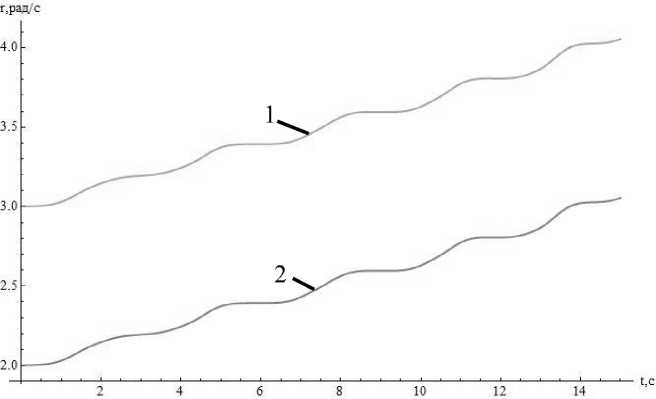
Рис. 3. Зависимость проекции угловой скорости r от времени: 1 — численное решение; 2 — аналитическое решение.

На рисунках 1–3 кривые полностью совпадают, но для наглядности одна кривая (численное решение) смещена вдоль вертикальной оси на единицу. Графики показывают, что результаты численного и аналитического решения совпадают.

Заключение

В результате выполнения работы построена математическая модель движения относительно неподвижной точки твердого тела с полостью, целиком заполненной жидкостью большой вязкости (1). Данная модель представлена динамическими уравнениями. При необходимости исследования ориентации тела в пространстве к этим уравнениям добавляются любые кинематические уравнения (в углах Эйлера, в направляющих косинусах, в кватернионах и т. д.). Уравнения (1) записаны для твердого тела любой формы, что расширяет их применимость. Для случая динамической симметрии твердого тела получены упрощенные уравнения (2), позволившие найти первый интеграл движения (5) и точное аналитическое решение типа (6) с учетом (11), (12) и (13). Как показывают графики на рисунках 1–3, полученное аналитическое решение полностью совпадает с результатом численного расчета, из чего можно сделать вывод о правильности решений.

Полученные аналитические зависимости для амплитуд x и z показывают, что на большом интервале времени они стремятся к постоянным значениям: амплитуда x стремится к нулевому значению, амплитуда z к величине K/C . Данный факт говорит о том, что диссипативные свойства жидкости внутри твердого тела обеспечивают перераспределение кинетического момента так, что он перенаправляется вдоль продольной оси (оси динамической симметрии) твердого тела.