Аналитическое решение контактной задачи о внедрении сферического индентора в мягкий упругий слой

Введение. Контактные задачи для упругого слоя на протяжении длительного периода времени привлекают внимание исследователей. Решения этих задач имеют многочисленные приложения, в частности, они эффективно используются при исследовании свойств износостойких и защитных покрытий. Одним из важных практических приложений является возможность интерпретировать результаты индентирования и наноиндентирования [1]. Результаты работы могут быть использованы при изучении упругих свойств мягких материалов (мягкие полимеры, биологические ткани), когда следует учитывать влияние жёсткости подложки на образец.

Решению контактных задач для упругого слоя посвящено большое количество работ, так, например, в [2] постановка классической задачи Герца обобщается, и рассматривается случай, когда сферический индентор вдавливается в слой, лежащий на недеформируемом основании или на однородном полупространстве (однородное полупространство имеет упругие свойства, отличные от упругих свойств слоя). Задача сводится к решению интегрального уравнения. Приближённое решение интегрального уравнения строится двумя методами: сингулярным методом, который эффективен для очень тонких слоёв, лежащих на недеформируемом основании, когда толщина слоя К меньше радиуса контакта а (Л = К / а <0,5), и регулярным методом, который применим в случае, когда толщина слоя такова, что А > 1 [3].

В данной работе для решения контактной задачи о внедрении сферического индентора в мягкий однородный слой на жёстком упругом полупространстве используется двустороннеасимптотический метод [4, 5]. Под мягкостью слоя следует понимать то, что модуль Юнга рассматриваемого слоя в несколько раз меньше модуля Юнга подстилающего полупространства. За это отличие упругих модулей основания и слоя отвечает параметр относительной жёсткости ос-

‘Работа выполнена при частичной поддержке РФФИ (11-08-91168-ГФЕН_а, 12-07-00639_а) и Министерства образования и науки РФ (ГК № 11.519.11.3028, соглашения № 14.В37.21.1131, 14.132.21.1693).

кования п (относительной мягкости слоя), равный отношению соответствующих упругих модулей. Ниже рассмотрены случаи, когда параметр п = 2,5; 10; 100; 1000 и показано, что при увеличении значения этого параметра результаты, полученные двусторонне-асимптотическим методом, сходятся к известным решениям, полученным ранее [6] для недеформируемого основания. Используемый метод позволяет получить эффективное решение задачи во всём диапазоне значений характерного геометрического параметра задачи Л.

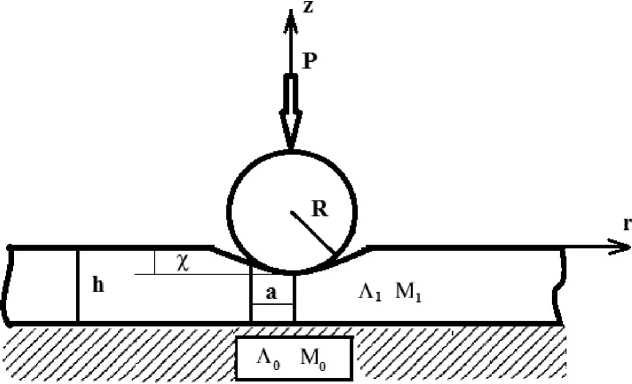
Рис. 1. Постановка задачи

Постановка задачи. Пусть сферический индентор вдавливается в поверхность мягкого упругого однородного слоя, сцепленного с упругим жёстким полупространством, силой Р (рис 1). С полупространством связана цилиндрическая система координат (r^,z). Предполагается, что все деформации упруги и размер зоны контакта а мал по сравнению с радиусом R сферы, описывающей форму индентора. Силы трения между индентором и поверхностью полупространства отсутствуют. Считаем, что в окрестности начальной точки контакта форма сферического индентора аппроксимируется параболой z = ip(r) = pr2 (1)

Аппроксимация обоснована для однородных тел [7] для малых радиусов контакта а < 0,1/?. Это условие выполняется практически для всех случаев упругого сферического внедрения. Вне индентора поверхность полупространства не загружена. Под действием силы Р индентор перемещается на расстояние х вдоль оси z. Коэффициенты Ламе изменяются с глубиной по следующему закону:

• 1)    /1 = 4, М = M_V -Н

• 2)    /1 = Д, М =М₀, -®

При сделанных предположениях граничные условия будут иметь вид:

[о =0,                    r>a                [ т⁽¹⁾ = т⁽²⁾, о⁽¹⁾ = о⁽²⁾

ф [и/ = -б(г) = -(х-ф(г)),г<а             р1) = w(2), а(1) = а(2)

При (г; - z) ^ да напряжения в полупространстве исчезают. Требуется определить перемещение штампа и распределение контактных нормальных напряжений под штампом:

^1=0 ="Ч(^ГУ ^г-^а-                            (3)

Построение решения задачи. Используя метод интегральных преобразований, задача сводится к решению следующего интегрального уравнения [4]:

J т (_Р) pd_P J L (u ) J_o (urX¹) J_o (ирХ¹ ^du = Л0_О (0)Г(г), г < 1 о                   о                                                 '

Здесь трансформанта L^ строится численно методом моделирующих функций [8].

В [4, 5] описан метод аппроксимации трансформанты ядра уравнения выражениями вида

/=1 U + Dj              k=x U + Uk где Д, В,, Dk е С; CkeR — некоторые константы

Для трансформанты ядра Ци^е1^ в работе [4] получено аналитическое выражение, ко торое служит для приближённого определения контактных напряжений и вдавливающей силы:

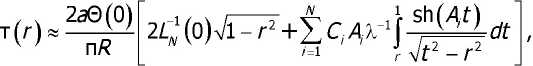
0<г<1,

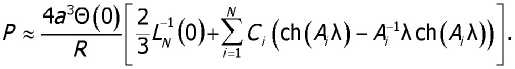
Неизвестные С, определяются из решения системы линейных алгебраических уравнений [4].

При рассмотрении контактной задачи о взаимодействии штампа с упругим слоем, лежащим на упругой подложке, в случае существенного отличия свойств слоя и подложки, использовалось предположение, что слой лежит на недеформируемом основании [3, 6]. Для этой модели основания трансформанта ядра ЦО) = 0.

Одним из условий использования двусторонне-асимптотического метода является то, что трансформанта ядра является всюду строго положительной, и более того, нигде не обращается в ноль. Предположение, что подложка под покрытием остаётся упругой, хотя её свойства отличаются от свойств покрытия в 100,1000, и более раз, позволяет удовлетворить этому условию.

Ниже считаем, что основание, на котором лежит слой, остаётся упругим, хотя его упругие свойства значительно отличаются от упругих свойств покрытия.

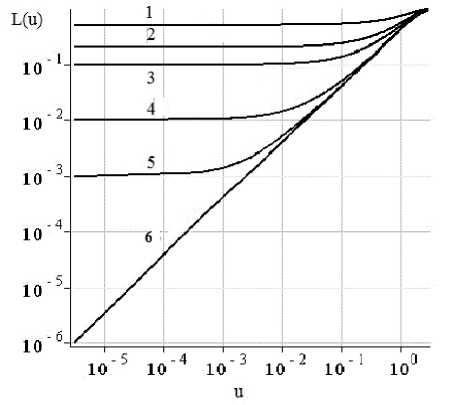
Рис. 2. Трансформанты ядер интегрального уравнения. Кривые 1—5 соответствуют отличию модулей Юнга слоя и основания в 2,5; 10; 100; 1000 раз соответственно. Кривая 6 соответствует трансформанте ядра для недеформируемого основания

На рис. 2 изображены графики функций L^ — трансформант ядра интегрального уравнения (4), построенные методом моделирующих функций [8]. Графики изображены в логарифмической шкале по обеим осям. Кривые с номерами 1,2, 3,4, 5 соответствуют трансформантам ядра для материалов, у которых упругие свойства покрытия и подложки отличаются в 2, 5, 10, 100, 1000 раз соответственно. Номером 6 обозначен график трансформанты ядра, для случая неде-формируемого основания, при построении которого была взята функция из [3], следующего вида: , .      2xsh(2u)-4u                   „

L (и) =------₇₅₇, где х = 3 - 4 V.

2xch(2u) + l + x +4и

Анализируя рис. 2 можно увидеть, что по мере того, как увеличивается жёсткость основания, графики функций трансформант приближаются к своему предельному графику 6, для недефор-мируемого основания. Покажем, что значения контактных напряжений с увеличением жёсткости подложки приближаются к контактным напряжениям, соответствующим недеформируемой подложке.

Численные примеры. Рассмотрим внедрение параболического индентора в однородный слой, лежащий на жёстком упругом основании. Параметр п, характеризующий относительную жёсткость, принимает значения 2,5; 10; 100; 1000 (n = f₀(^i(^)) )■ Коэффициент Пуассона, не нарушая общности, полагаем равным 0,3.

Введём функцию ДА(и), характеризующую погрешность аппроксимации трансформан ты ядра:

А (“) = IW (и) - Ц^Ц -100 %.                   (8)

Формула (8) введена для оценки погрешности аппроксимации трансформанты ядра выражениями вида (у).

В таблице 1 приведены значения величины т* =2/?т(О)/0_о(О)а, характеризующей контактные напряжения под штампом в точке г= 0.

Таблица 1

Контактные напряжения

max А, (и), и е [0..оо)	1,4 %	2,8 %	3,3 %	3%	3,2 %	—
/V	8	8	10	10	20	—
П	2	5	10	100	1000	—
Л = 0,25	4,098	6,375	7,991	10,075	10,326	10,342*
Л = 1	2,866	3,144	3,252	3,342	3,389	3,305'
Л = 4	2,562	2,555	2,560	2,556	2,542	2,568т

В таблице 2 приведены значения величины Р* = 2RP/Q₀ (0)а³, определяющей связь между вдавливающей силой и радиусом сферы.

Таблица 2

Связь вдавливающей силы и осадки

п	2	5	10	100	1000	—
Л = 0,25	7,938	11,557	13,973	17,048	17,447	17,66т
Л = 1	5,895	6,365	6,553	6,709	6,771	6,8 2Т
Л = 4	5,363	5,355	5,365	5,360	5,336	5,38т

Результаты из работы [6] для недеформируемого основания.

В таблице 1 и 2 значения крайнего правого столбца взяты из монографии [6] и характеризуют т* и Р* для случая вдавливания параболического штампа в упругий слой, лежащий на не-деформируемом основании.

Из анализа таблицы 1 видно, что максимальная разница между контактными напряжениями при п = 1000 и значениями для недеформируемого основания не превышает 3 % при Л = 1. Заметим, что из таблиц 1, 2 видно, что значения т* и Р* принимают близкие значения при П = 100 и п = 1000. Обратим внимание также на то, что упругие свойства основания не оказывают сильного влияния на распределение контактных напряжений, для значений параметра Л > 1 (если сравнивать значения напряжений при п, равном 2 и 1000, то максимальная разница не превышает 15 % для Л = 1).

Заключение. Использование двусторонне-асимптотического метода при решении осесимметричной контактной задачи о мягком упругом слое на жёстком основании позволяет учесть деформируемость подложки под мягким покрытием твёрдого основания и получить решение, эффективное для всего диапазона значений характерных геометрических и физических параметров задачи, что является важным при исследовании механических свойств биологических тканей и мягких полимеров.

Автор благодарит С. М. Айзиковича за постановку задачи и советы при реализации решения.