Аналитическое решение задачи измерения мощности шумящего источника комбинированным приемником на фоне сосредоточенной и изотропной помех

Электронный журнал «Техническая акустика»

Федеральное государственное унитарное предприятие «Всероссийский научноисследовательский институт физико-технических и радиотехнических измерений» (ВНИИФТРИ), , e-mail:

Рассматривается простой алгоритм, позволяющий одновременно производить пеленг в плоскости двух некогерентных акустических сигналов комбинированным приемником колебательной скорости. Исследуется работа алгоритма в присутствии изотропной помехи. В результате обработки согласно алгоритму модельных сигналов показано, что, например, для двух сосредоточенных источников с одинаковой средней интенсивностью и углом между направлениями на них из точки приема 45° алгоритм не теряет работоспособность даже в присутствии изотропной помехи с уровнем в точке приема на 6 дБ выше, чем у одного из источников. Методический подход, заложенный в алгоритме, позволяет менять свойства алгоритма и, следовательно, произвести его оптимизацию.

Пусть в нашем распоряжении имеется комбинированный акустический приемник [1], принимающий две компоненты колебательной скорости V _x , V _y и акустическое давление P . Рассмотрим задачу, когда в присутствии изотропной помехи принимаемый сигнал формируется двумя источниками с колебательной скоростью в точке приема V ₁ n ^r ₁ и V ₂ n ^r ₂ .

N

Изотропная помеха создает колебательную скорость ^ U_tm_i , где число компонент i = 1

источников помехи N велико, а вектора единичной длины m ^r _i распределены случайным образом. Вектора с единичной длиной n ^r ₁ и n ^r ₂ направлены на источники, а значения сигналов являются случайными стационарными величинами, для которых: <  V 12 >^ E 1 ,

• <    V 22 >= E 2 ,

• <    V 1 V 2 >^ 0,

• <    U _i U _J>_i , _J = 0,

• < U _t U _t >= E 3 /N ,

где угловыми скобками обозначено усреднение по времени.

При расчетах удобно от векторов в плоскости перейти к комплексным числам n i = n₁ x + in i_y , где i — мнимая единица (для остальных векторов аналогично). Тогда

NN для принимаемого сигнала V = V1 n1 + V2n2 +^Uimi и Vp = V + V2 +^Ui , где i=1                                                      i=1

V p = P /( cp ), p — плотность среды, c — скорость звука. Обозначим символом * комплексное сопряжение и введем величины:

а =< V*V > -E3, в =< VVP >,                                                                    (1)

у =< VV > , причем в реальных измерениях время усреднения будет, разумеется, ограниченным. Тогда:

а = E₁ + E ₂, в = E ₁ n ₁ + E ₂ n ₂, Y = E₁ n 2 + E ₂ n ² .

Таким образом, изотропная помеха дает вклад только в величину <  V * V > . Действительная величина а и две комплексные величины в и / образуют в сумме пять действительных величин, из которых представляется возможным найти пять неизвестных: углы и интенсивности двух источников и интенсивность изотропной помехи. Будем временно считать, что величина E ₃ нам известна, и мы можем измерить величину а .

Обозначим Л = n * n ₂, тогда:

а =< V * V >  - E ₃, в =< VV p > , Y =< VV >  , E j + E ₂ = а , E ₁ + E ₂ Л = n * в , E 1 + E 2 ( Л )² = ( n * )² / .

Поделив разность (4) и (2) на разность (3) и (2), получим выражение

₂   ( ⁿ * )² Y ^{- n} * ^в

л =*

n1 в - а или

_ n*y - в n 2 = *о .

n ₁ в - а

Обозначим γ*γ-α2 ≡ µ, γβ* -αβ≡ sν и r ≡ n1s*, где ν — действительное число, а s — комплексный вектор единичной длины. Тогда, учитывая, что n2*n2 = 1, и умножая (5) на комплексно сопряженное выражение, получим r + r* = µν . Обозначив действительную часть числа r как cos(θ) , получим уравнение cos(θ) = µ (2ν) . (6)

С учетом того, что для измеренных сигналов и подсчитанных величин в результате погрешностей правая часть уравнения может оказаться как больше 1, так и меньше –1, в этих случаях решением (6) можно считать соответственно θ = 0 и θ = π . В остальных случаях уравнение дает два решения θ = θ ₀ и θ = - θ ₀ . Эти два решения дают вектора направлений на источники n ^r ₁ и n ^r ₂ , а после подстановки их в систему уравнений из действительных частей (3) и (4) можно найти и интенсивности источников E ₁ и E ₂ . Подставив E ₁ и E ₂ в (2) можно затем численно решить (1) относительно величины E ₃ , например, методом деления отрезка пополам.

Проверка работы алгоритма при численном моделировании дала неожиданный результат. В отсутствии изотропной помехи решение оказалось точным при любом времени усреднения и любых направлениях и интенсивностях источников. Результаты в присутствии помехи приведены ниже на рис. 1–7. При моделировании полагалось, что пеленг берется раз в 4 секунды в полосе 300 Гц, т. е. основывается на 2400 независимых измерениях сигналов. При определении средних значений и среднеквадратических отклонений сигналы моделировались 25 раз. При моделировании изотропной помехи для каждого измерения сигналов бралось 100 источников со случайными направлениями и случайными величинами колебательной скорости. Все случайные величины имели близкое к нормальному распределение (сумма 6 равномерно распределенных случайных величин).

На рис. 1–7 изображена усредненная разница истинного и рассчитанного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение рассчитанного угла (тонкая линия). При этом на рис. 1–2 уровень изотропной помехи считаем известным, а на рис. 3–7 этот уровень определяем по изложенному выше алгоритму (численным решением уравнения для E ₃ ).

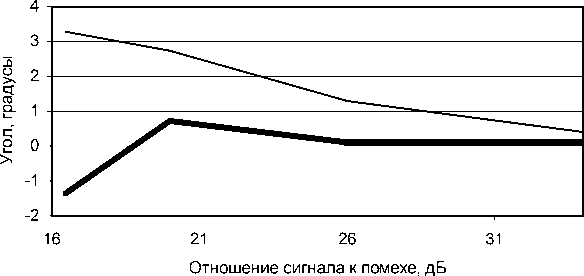
Рис. 1. Усредненная разница истинного (10°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (тонкая линия) в случае, если уровень изотропной помехи известен

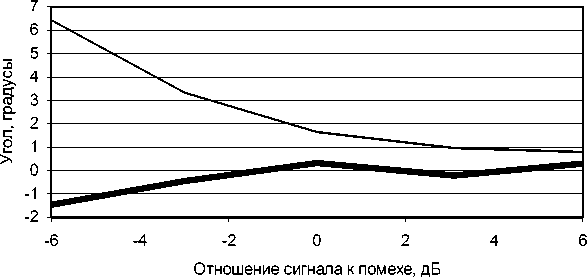
Рис. 2. Усредненная разница истинного (90°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (токая линия) в случае, если уровень изотропной помехи известен

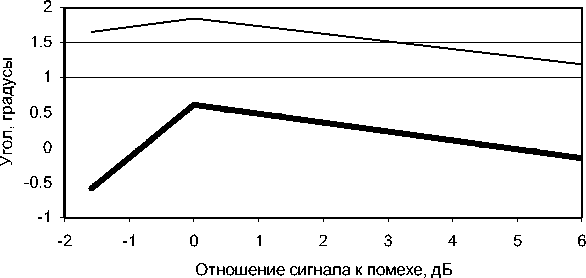
Рис. 3. Усредненная разница истинного (90°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (тонкая линия) в случае, если уровень изотропной помехи не известен и определяется изложенным выше способом

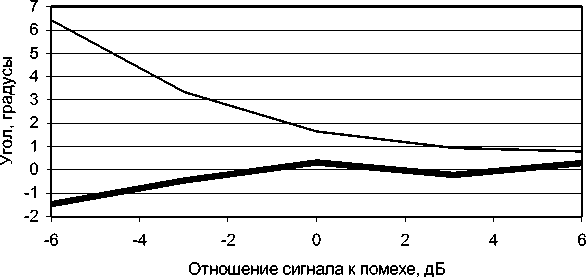
Рис. 4. Усредненная разница истинного (45°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (тонкая линия) в случае, если уровень изотропной помехи не известен и определяется изложенным выше способом

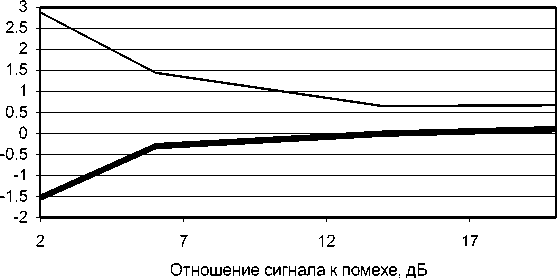
Рис. 5. Усредненная разница истинного (30°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (тонкая линия) в случае, если уровень изотропной помехи не известен и определяется изложенным выше способом

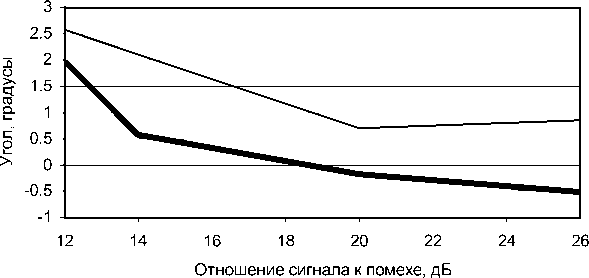
Рис. 6. Усредненная разница истинного (120°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (тонкая линия) в случае, если уровень изотропной помехи не известен и определяется изложенным выше способом

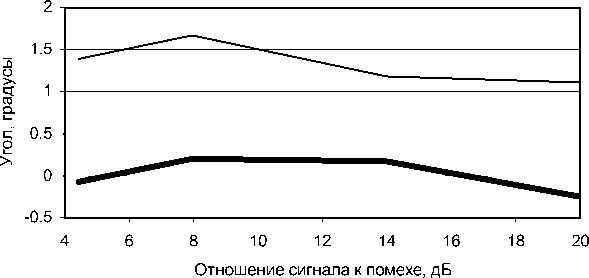
Рис. 7. Усредненная разница истинного (130°) и определенного угла между источниками равной интенсивности (жирная линия) и среднеквадратическое отклонение определенного угла (тонкая линия) в случае, если уровень изотропной помехи не известен и определяется изложенным выше способом

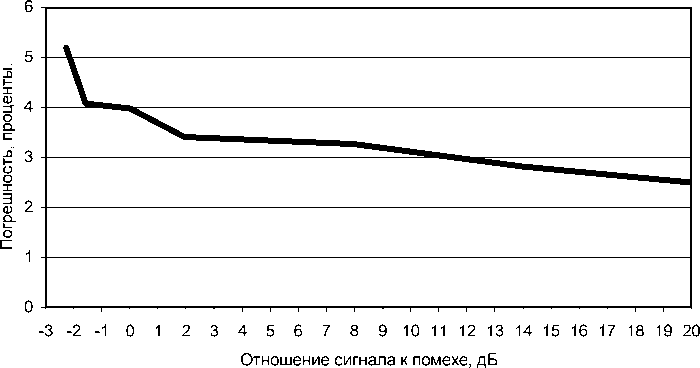
Рис. 8. Среднеквадратическая погрешность определения интенсивности источника №1 при угле между источниками 90° и равной интенсивности источников

ЗАКЛЮЧЕНИЕ

Попытка определить уровень изотропной помехи численным решением нелинейного уравнения относительно E ₃ по описанному выше алгоритму привела к существенным ограничениям в допустимом минимальном отношении сигнала к помехе и одновременно увеличила среднеквадратическое отклонение угла по сравнению со случаем, когда величина E ₃ заранее известна. Можно построить много различных оценок уровня изотропной помехи, выбирая по-разному подлежащую минимизации целевую функцию. Выбор оптимальной оценки требует отдельного исследования. Для углов между двумя источниками сигнала равной интенсивности, больших или равных 140° алгоритм работать перестает (при угле 139° он еще работает). Причина такого поведения алгоритма пока не понятна.

Рассмотренный выше алгоритм решения, кроме того, видимо не является наилучшим в смысле погрешностей, связанных с конечным временем усреднения. Так, мы могли, например, определить величину а как а =< V p V_p > . При бесконечном времени усреднения это даст тот же результат, а при конечном — другой. Однако вышеизложенный алгоритм привлекает простотой и явными аналитическими выражениями для вычисляемых величин. Он может быть использован, например, в качестве стартовой оценки перед применением к исходным уравнениям более точных численных методов, минимизирующих погрешность результата.

На рис. 1–7 обращает внимание довольно небольшая величина среднеквадратического отклонения определенного согласно алгоритму угла между источниками сигналов. Это позволяет предположить возможность построения более точных несмещенных оценок пеленга источников сигнала, например минимизацией функционала в методе наибольшей вероятности. Предлагаемый метод в сочетании с описанным в работе [2] может быть после необходимого модельного и экспериментального исследования использован в практике гидроакустических измерений.