Аналитическое решение задачи о формообразовании шаровых пробок путем обжима трубных заготовок в полусферических матрицах

Введение . В настоящее время широкое применение в различных отраслях промышленности и энергетики находят шаровые краны. Зачастую они изготавливаются из дорогостоящих коррозионностойких материалов, поэтому предъявляются повышенные требования к их металлоемкости.

Существенный вклад в себестоимость крана вносит запорный орган – шаровая пробка (по данным работы [1], ее стоимость составляет до 40 % от стоимости всего крана). Поэтому наиболее выгодным с точки зрения металлоемкости является изготовление тонкостенных пробок.

Эффективным способом изготовления шаровых пробок является обжим в полусферических матрицах [2] по технологии, предложенной авторами работы [3] с некоторыми изменениями. Суть этой технологии состоит в следующем.

Заготовка в виде тонкостенной трубы обжимается полусферическими матрицами в два перехода так, что на ее торцах формируются полюсные отверстия. Сначала обжимают один торец, после чего устанавливают подкрепляющую трубу, образующую проход, и обжимают второй торец (рис. 1).

Указанный способ изготовления пробок внедрен в производство авторами работы [1]. Использование способа формообразования в два перехода в отличие от [3] обосновывается большей технологичностью. Это позволяет достичь большей симметрии формируемой заготовки относительно экватора.

Отработка этой технологии вызвала ряд проблем, без теоретического решения которых затягивался процесс определения рациональных параметров исходных заготовок и прессового оборудования. Например, на первом переходе цилиндрическая часть заготовки нередко обретала осесимметричную форму выпучивания, а процесс формообразования требовал порой неоправданно завышенных усилий пресса. Последнее наводило на мысль о проблемах с трением.

Представленные в литературе аналитические решения [4–6] для описания указанной технологии обладают ограниченной применимостью в плане используемых моделей трения и описания диаграммы деформирования. Предлагаемое решение позволяет использовать эмпирические модели трения и механических свойств материала, а потому обладает большей достоверностью.

Для описания первого перехода рассмотрим задачу формообразования сферической оболочки с полюсными отверстиями из относительно тонкостенной (R/H > 6,5) цилиндрической трубы путем пластического деформирования ее в полусферических матрицах в два перехода. В качестве допущения примем, что в результате деформирования диаметр цилиндрической заготовки становится экватором сферической оболочки (см. рис. 1, а).

Предварительные размышления о возможном развитии процесса пластического деформирования цилиндрической оболочки сошлись в последовательность взаимосвязанных задач [2].

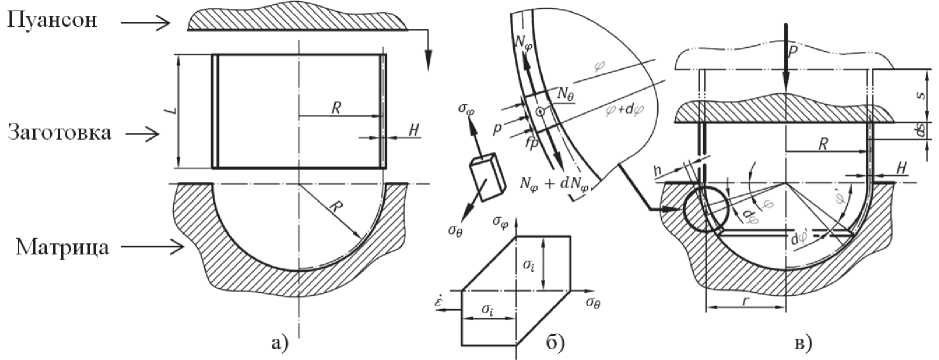
Рис. 1. Схема изготовления однослойной шаровой пробки: а – заготовка перед началом первого перехода; б – условия равновесия и ассоциированный закон течения; в – заготовка в деформированном состоянии; г – заготовка перед началом второго перехода; д – завершающие стадии обработки изделия

• 1.    Проблема трения и контактного взаимодействия заготовки с поверхностью матрицы по мере заглубления ее торца с обжатием до диаметра полюсного отверстия требуемого размера (определяется углом φ^′, который изменяется в пределах 0≤φ^′ ≤ φ^′_к, см. рис. 1, в).

• 2.    Определение напряженно-деформированного состояния сферической оболочки за зоной краевого эффекта, где она оказывается под действием поверхностной нагрузки, удовлетворяющей условиям существования напряженного состояния близкого к безмоментному.

• 3.    Оценка влияния предварительного нагрева заготовки, о целесообразности которого говорится в работе [7], на максимальное усилие пресса в процессе формообразования.

• 4.    Предотвращение возможной потери устойчивости цилиндрической части заготовки в процессе первого перехода.

В представленной работе рассмотрены первые два пункта указанного списка.

Ранее, в работе [2], было предложено аналитическое решение задачи об определении усилия при формообразовании P в предположении конечных осесимметричных перемещений оболочки, описываемых лагранжевыми координатами. Примем это решение в качестве первого приближения. При описании деформированного состояния учтем только пластические деформации, связанные с напряжениями законом нелинейного упрочнения, определяемым диаграммой деформирования материала при заданной скорости приложения нагрузки. Систему уравнений, содержащую условия равновесия безмоментной теории, физические и геометрические соотношения, путем замены переменных сведем к задаче Коши для линейного неоднородного дифференциального уравнения, интегрирование которого позволяет представить усилие штампа в виде функционала, зависящего от механических характеристик материала и закона трения. Решение основано на следующих допущениях.

Основные допущения . Кинематические соотношения. Цилиндрическая оболочка (см. рис. 1, а) с исходной длиной L, толщиной H и радиусом срединной поверхности R в процессе формообразования переходит в сферу с радиусом срединной поверхности R. При погружении заготовки в матрицу, определяемом угловой координатой ф‘ (см. рис. 1, в), ход пуансона составляет s. Полагаем, что пластическое деформирование материала заготовки имеет место только внутри матрицы, вне ее деформации равны нулю. Толщина в сечении, определяемом угловой координатой ф, принимает некоторое значение h. Для этого сечения

• r = R cos(ф).                                                                                (1)

Принимаем гипотезу несжимаемости:

e g + ^e ф + e r = 0,                                                                             ⁽²⁾

где e g = ln(1 + е_е) = ln(r/R), е_ф = ln(1 + S ф ), e r = ln(1 + S r ) = ln(h/H);

e_g, e_ф, e_r - соответственно, окружная, меридиональная и радиальная логарифмические меры деформации; Е_е, е_ф , е_г - соответственно, окружная, меридиональная и радиальная инженерные меры деформации.

Объем погруженного в матрицу кольцевого элемента оболочки, определяемого дугой R dф равен объему кольца высотой ds:

2пг h (r + ^^) dф' = 2nR H ds, откуда получаем связь между обобщенными координатами rh (1 + ^) dф' = H ds.

Условия равновесия. Для описания равновесия сферической оболочки (рисунок 1, б) используем соотношения безмоментной теории [4]:

Ng = agh; Nф = ^h; Nr = ^h = 0;

Ng + Nф + p R = 0; r ^ + Ng tg(ф) = f(p) P R, тем самым, в соответствии со статической теоремой предельного равновесия [4], получим ниж- нюю оценку усилия пресса.

Величина коэффициента трения f будет определена в последующем законом трения f(p) [8]. В первом приближении принимаем закон трения

f(p) = f = const = 0,2 ... 0,5.

Физические соотношения. Процесс приложения нагрузки считается монотонным: интенсивность напряжений а в каждой точке возрастает или остается постоянной, то есть Йф > 0.

В соответствии с инженерным подходом к решению задачи о течении тонкого слоя металла по жесткой поверхности [8], полагаем, что главные напряжения при установившемся течении равны

О 1 = 0;    0 2 = о_ф;        0 3 = О е .

Задавшись условием текучести Треска-Сен-Венана, получим

O i = О 1 - 0 3 = -О е .

В соответствии с ассоциированным законом течения [4] при реализуемом плоском напряженном состоянии скорость пластической деформации в меридиональном направлении равна нулю Еф = 0 (см. рис. 1, б). Непосредственным следствием из этого является условие eф = 0 [4]. В таком случае условие несжимаемости (2)–(3) приобретает вид:

eg + er = ln (^) = 0.(9)

Это условие с учетом выражений (1)–(2) можно представить в форме eg = ln(cos(ф)) ; er = —eg = — ln(cos(ф)) ; eф = 0; rh = RH = const; h = H/cos (ф) .

Разрешающие уравнения . Непосредственная подстановка условий (8), (10) в уравнения (5)–(6) приводит к системе уравнений

£ + f Y = 5a* — tg№ (ф);

аф йф

О ф = О 1 ⁽ф) — Y; o_e = —О 1 ⁽ф⁾; Y = ^ = ^cos^).

Первое соотношение системы (11) является линейным неоднородным дифференциальным уравнением первого порядка с постоянными коэффициентами относительно новой переменной Y, имеющей размерность напряжения. Граничное условие – отсутствие меридиональных напряжений на краю сферы – представим в виде

Y(φ^′) = σ i (φ^′).                                                                                            (12)

Решая задачу Коши для уравнений (11)–(12), находим выражение для определения вспомогательной переменной

Y=σ^(φ) +exp(-fφ) ∫φφ′exp(fφ)^f+tg(φ)^σ^(φ) dφ, а затем компоненты напряженного состояния и поле давлений

σφ =-exp(-fφ) ∫φφ exp(fφ)(f+tg(φ)) σi(φ) dφ; σθ = -σi(φ);

p=^H_Rsec(φ) (σ i (φ) +exp(-fφ) ∫^φ_φ^′exp(fφ)(f+tg(φ)) σ i (φ) dφ).

Усилие формования и ход пуансона (см. рис. 1, а) оказываются связаны зависимостями ′

P=-2πRH σφ(0) =2πRH∫0φ exp(fφ)(f+tg(φ)) σi(φ) dφ;

s=Rφ′ + H2 (φ′ -sin (φ′)).

Расход электроэнергии для пресса с коэффициентом полезного действия 1 на проведение одного перехода формообразования оценим по формуле

W=¹_η∫Pds=¹_η∫₀^φ′кPR[1+ ^H(1-c ₂ ^o _R ^s(φ)) ] dφ^′ =

3′   ′

= R ∫0φк ∫0φ exp(fφ)(f+tg(φ)) σi(φ) [1+        φ ] dφ dφ′.(16)

η(H)2R

В полученном решении (13)–(16) неопределенной остается интенсивность напряжений как функция координаты φ. Компоненты деформированного состояния определены соотношениями (10). Задавая закон, связывающий интенсивности напряжений и деформаций, получаем выражение для интенсивности σi(φ).

Если в качестве меры интенсивности деформации принять интенсивность логарифмической деформации e^(φ) = ^√|^^^| = √^^ ln (sec(φ)), то зависимость интенсивности напряжения от интенсивности логарифмической деформации может быть аппроксимирована степенным законом [9]

σi(φ) =K[ei(φ)]m, или законом жесткого линейного упрочнения

σi(φ) =σs + E′ei(φ), где K – коэффициент прочности, m – показатель упрочнения, σs – предел текучести, E′ – модуль упрочнения – механические характеристики материала при заданной температуре и скорости приложения нагрузки.

Полученное решение позволяет также использовать при расчетах произвольный закон деформирования σi(ei(φ)), который можно найти в справочниках или получить путем простейшего эксперимента на растяжение или кручение стержневого образца.

Сопоставление с расчетами МКЭ . Осознанию применимости названных выше допущений способствовало рассмотрение процесса перехода цилиндрической оболочки в полусферу с помощью его моделирования в прикладных конечно-элементных пакетах DEFORM и LS-DYNA (рис. 2–4). Именно здесь была обнаружена зависимость решения от значения коэффициента трения, завышение которого оказалось чреватым с точки зрения получения устойчивого решения задачи.

В качестве простейшей модели, на которой производилось сопоставление конечно-элементного и аналитического решений, была рассмотрена осесимметричная модель с десятью элементами по толщине (R/H = 15,5; диаметр матрицы D = 160 мм). Материал конечно-элементной модели имел билинейную кривую деформирования [4] с модулем упругости E=2∙10^ МПа, пределом текучести σ^ = 500 МПа и модулем упрочнения E′ = 800 МПа; в аналитической модели использован жестко упрочняющийся материал (E=∞) с теми же параметрами. Остальные параметры представлены на рис. 2.

Оценка усилия формования с использованием представленной теории оказалась весьма точной вплоть до потери устойчивости процесса деформирования (см. рис. 2). По достижении без- моментными составляющими осевых напряжений величины предела текучести и в том и в другом пакетах МКЭ наблюдалось осесимметричное выпучивание заготовки, которое в дальнейшем сопровождалось падением осевых усилий. Этот факт подтверждается экспериментальными данными, имеющимися в работах [3, 5].

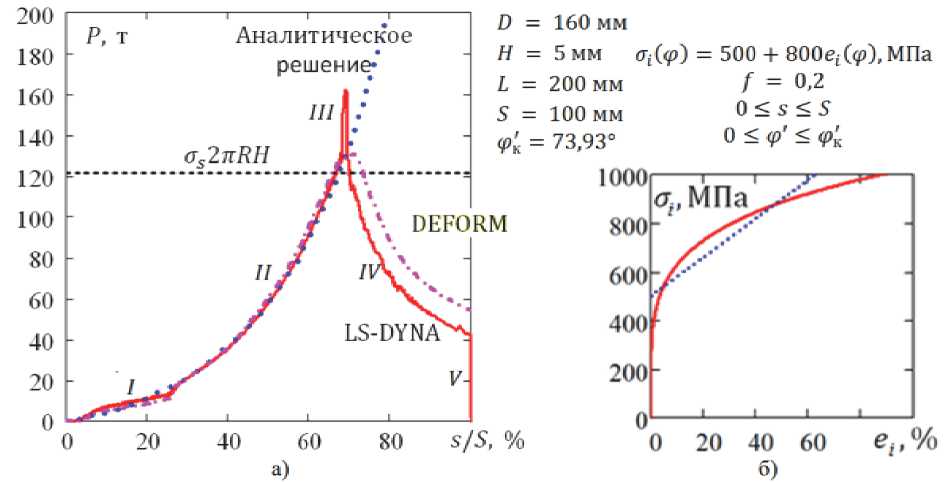
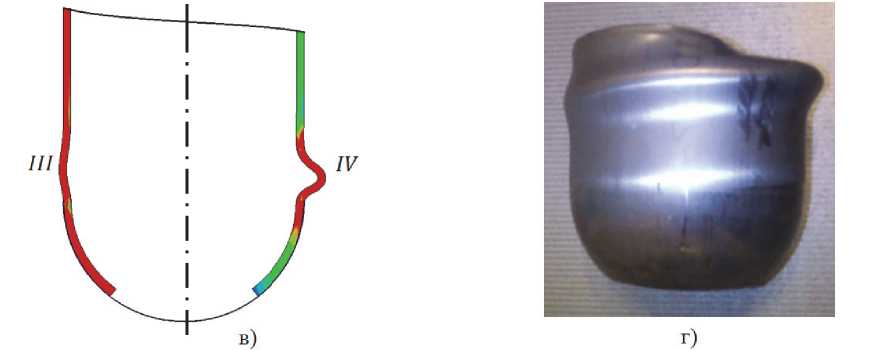
Рис. 2. Сравнение результатов расчета усилия пресса при формообразовании сферы: а) сопоставление аналитического и конечно-элементных решений; б) аппроксимация диаграммы деформирования законом линейного упрочнения; в) механизм потери устойчивости; г) заготовка, потерявшая устойчивость в процессе формования. Цифрами обозначено: I – этап неустановившегося деформирования; II – установившееся течение (применима безмоментная теория); III – потеря устойчивости течения, перераспределение напряжений; IV – изгибное деформирование по осесимметричному механизму; V – снятие нагрузки

На рис. 3 показаны графики изменения в процессе формообразования м еридиональных напряжений в конечных элементах по толщине заготовки для трех поперечных сечений – на расстоянии 5, 30 и 60 мм от края, погруженного в штамп, и графики изменения меридиональных моментов, создаваемых этими напряжениями. Наилучшее соответствие безмоментных компонент напряжений в аналитическом (точки) и конечно-элем е нтном (сплошная линия) решени я х достигается на участке II, который отвечает пребыванию сечения внутри штампа в рамках ста б ильного деформирования. Участок III соответствует неустойчивому поведению загот о вки, которое проявляется в виде смены знака изгибающего момента. При отсутствии неустойч и вых эффектов аналитическое решение прогнозирует закономерный рос т (по абсолютному значению) безмомент-ной компоненты напряжения. Участок I – экстраполяция решения на цилиндрическую часть заготовки.

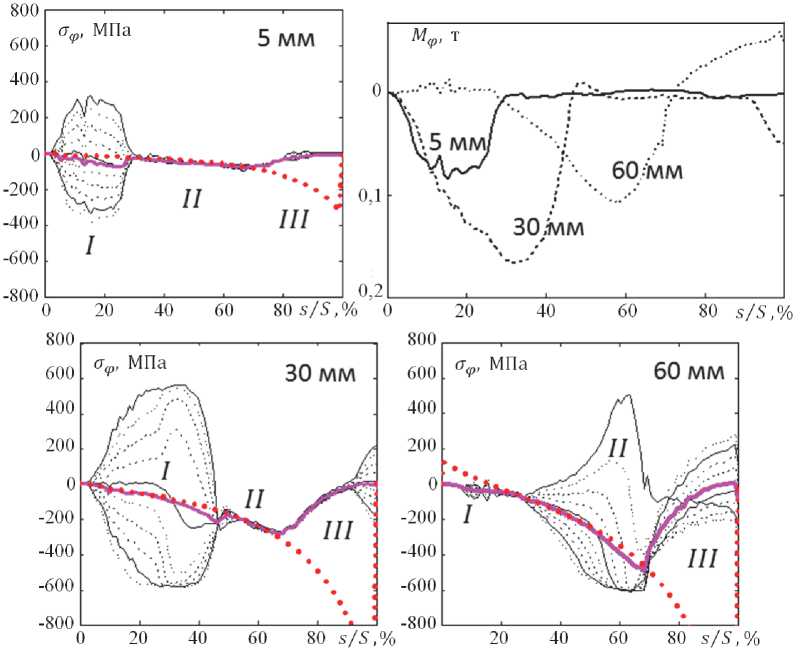
Рис. 3. Изменение меридиональных напряжений и изгибающих моментов в процессе формования заготовки по первому переходу для сечений, находящихся на расстоянии 5, 30 и 60 мм от торца, погруженного в матрицу

В специализированной литературе, посвященной теории тонколистовой штамповки [4-6], имеются аналитические решения для задач напряженно-деформированного состояния заготовок из идеально упругопластического материала, обжимаемых в матрице с криволинейной образующей.

Так, для случая полусферической матрицы при безмоментном напряженном состоянии предлагается следующая оценка осевого напряжения в заготовке [6]:

σφ = -σs(1 + f)(1 - Rrз), где R3 — радиус срединной поверхности заготовки; os - предел текучести.

Для учета изгиба вводится энергетическая поправка на работу изгибающих моментов в зоне очага деформации:

д = ^м ф = 40 s H ² = 40 s H

σφ HRφ   HRφ    Rφ , где Rv - радиус срединной поверхности полусферы. С учетом допущения Rv = R3 = R и поправки на изгиб, предложенное решение имеет вид

σφ =-σs [(1 + f)(1 - cos φ′) + 4RH].

Это решение отличается от предлагаемого в данной работе, поэтому для установления справедливости того или иного решения был произведен конечно-элементный расчет (параметры всех рассматриваемых моделей сведены в табл. 1). Рассчитанные методом конечных элементов значения усилий оказались примерно на 60 % больше теоретических (20) во всем интервале углов ф, а в момент достижения осевыми усилиями в МКЭ модели величины предела текучести (с последующим осесимметричным выпучиванием) отличие составило 63 %. В то же время различие между расчетами по формуле (14) и МКЭ для участка стабильного течения не превзошло 10 %, а с введением поправки на изгиб разница уменьшилась до значения менее чем в 5 % (рис. 4, а).

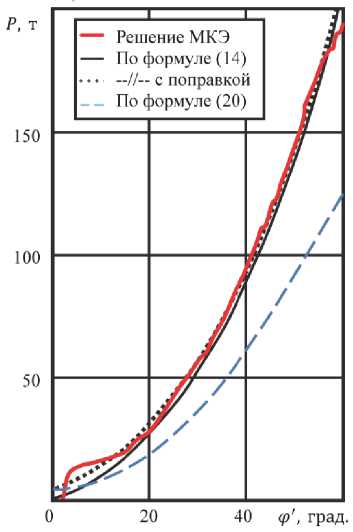
а)

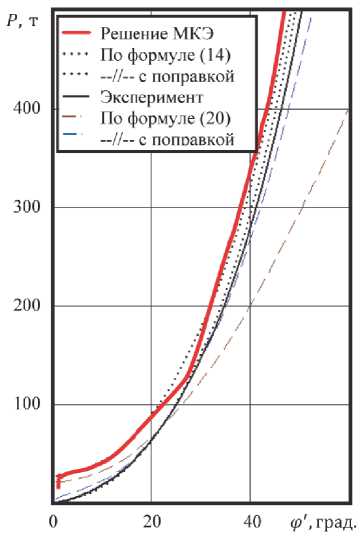
б)

Рис. 4. Сопоставление аналитических и конечно-элементной оценок осевого усилия при формировании заготовок из идеально-упругопластического материала (а) и материала со степенным упрочнением (б)

Схематизация свойств материала идеальной упругостью и пластичностью оказывается при- менима лишь при слабом упрочнении. Для высокопластичных (ψ >50 %) и сильноупрочняю- щихся (m > 0,2) сталей, используемых при изготовлении шаровых пробок, более правильной является схематизация свойств в виде закона степенного упрочнения (18).

На рис. 4, б представлены результаты расчета усилия формования для заготовки из стали 12Х18Н10Т (R/H = 7,5), полученные с использованием МКЭ и формул (14) и (20). В формуле (20) величина σ^ в одном случае положена равной пределу прочности материала (σв = 639 МПа), а в другом случае – равной интенсивности напряжений σ^(φ′). Как и в случае идеально пластичного материала, оценки усилия с использованием зависимости (20) оказываются существенно заниженными.

Рис. 5. Пересчет угловых координат в ход пуансона для материала со степенным упрочнением

Различие между оценкой усилия по предлагаемой методике и расчетом М КЭ на этот раз оказывается более заметным, что связано с высокой изгибной жесткостью сечения, опре д еляемой отношением H/R. Для уточнения аналитической оценки предлагается ввести поправо ч ное слагаемое

∆P = 2πRH∆σφ = 8πσi(φ′)H2, с учетом которого разница между аналитическим и МКЭ решениями снижается до 5 % при φ′ = 45°. Экспериментальная характеристика лежит между оценками (14) и (20), что связано с нелинейными особенностями трения.

Таблица 1

Исходные данные для аналитических и МКЭ моделей

Материал	Идеально упругопластический
Величина	Модуль упругости	Предел текучести	Модуль упрочнения	Коэффициент Пуассона	Длина заготовки	Наружный диаметр заготовки	Толщина заготовки	Ход полуматрицы	Коэффициент трения
Обозначение	E, МПа	σ ^ , МПа	E ′ , МПа	μ	L, мм	2R, мм	H, мм	S, мм	f
№ п/п
1	2∙10 ^	200	0	0,3	200	160	5	90	0,20
Материал	Линейно упрочняющийся
Величина	Модуль упругости	Предел текучести	Модуль упрочнения	Коэффициент Пуассона	Длина заготовки	Наружный диаметр заготовки	Толщина заготовки	Ход полуматрицы	Коэффициент трения
Обозначение	E, МПа	σ ^ , МПа	E ′ , МПа	μ	L, мм	D, мм	H, мм	S, мм	f
№ п/п
2	2∙10 ^	500	800	0,3	200	160	5	100	0,20
Материал	Со степенным упрочнением
Величина	Модуль упругости	Коэффициент прочности	Показатель упрочнения	Коэффициент Пуассона	Длина заготовки	Наружный диаметр заготовки	Толщина заготовки	Ход полуматрицы	Коэффициент трения
Обозначение	E, МПа	K, МПа	m	μ	L, мм	D, мм	H, мм	S, мм	f
№ п/п
3	2∙10 ^	1127	0,23	0,3	71	80	5	34	0,20

Уточнение закона трения . При решении задачи предполагалось, что трение подчиняется закону Амонтона, то есть поверхностное касательное сопротивление прямо пропорционально поверхностному нормальному давлению. Однако большинство теоретических и экспериментальных работ, включая [7, 8, 10], указывают на более сложный характер эффектов трения.

Анализ законов граничного трения, представленный в работе [2], позволяет рассматривать закон Амонтона как верхнюю оценку сопротивления трения. Фактический же закон трения τ(p) обладает экспоненциальным насыщением [7, 8].

Уточним решение (14) с использованием закона трения, предложенного А.Н. Левановым [7], и представленным В.Л. Колмогоровым в виде [8]:

τ=k п τ _s[1 - exp (-1,125 p/σ _s)], (21) где σ_s = ^σв+ ₂ ^σ0,2 – предел упрочнения материала заготовки; τ _s = 0,58 σ_s; k_п =0,05…1,0- константа поверхности, зависящая от условий проведения испытаний и качества обработки поверхности инструмента и заготовки. При рассмотрении закона Амонтона как верхней оценки трения, из разложения выражения (21) в степенной ряд следует, что f = 0,6525 k_п [2]. Эмпирический коэффициент 1,125 в выражении (21) соответствует варианту этой зависимости, представленному в работе [8], и отличается от значения 1,25 в работе [7].

Уточненное решение . В действительности радиус формируемой сферы R оказывается несколько большим, чем радиус заготовки R_з . Практически при построении характеристики формообразования в виде зависимости P(φ′) это может быть учтено введением поправочного угла

φз = arccos(Rз/R), такого, что при значениях φ′ <φз усилие формования оказывается нулевым. Оставшаяся часть характеристики может быть разбита на участки стабильного и нестабильного прилегания заготовки к матрице. Анализ результатов МКЭ расчетов показывает, что при φз ≤φ′ ≤ 30° осуществляется частичное прилегание к матрице, а при φ′ > 30° заготовка практически полностью прилегает к матрице.

С учетом непостоянства начального участка характеристики предлагается вести расчеты только для участка стабильного прилегания – при φ′ > 30°. При этом вид характеристики практически не зависит от параметра φз.

Проведенный анализ с использованием безмоментной теории (13) показал, что для стали 12Х18Н10Т с механическими характеристиками K = 1127 МПа и m = 0,23 [9] безмоментные компоненты нормальных давлений на участке стабильной характеристики 30° ≤ φ′ ≤ 50° при относительных размерах заготовки 6,5 ≤ R⁄H ≤35 укладываются в интервале 50 МПа < р < 200 МПа, а при 6,5 ≤ R⁄H ≤16 в интервале 100 МПа < р < 200 МПа.

В этих интервалах нормальных давлений закон трения (21) может быть аппроксимирован линейной зависимостью по Кулону:

τ=τ a +f 1 p,                                                                        (22)

где τa – в предположении И.В. Крагельского [10] составляющая сил сопротивления, обусловленная адгезией между поверхностями инструмента и заготовки, f1 – коэффициент трения, возникающего за счет деформации поверхности заготовки микронеровностями штампа.

В отличие от И.В. Крагельского, определявшего компоненты трения τa и f1 по отдельности, будем полагать, что обе они однозначно определяются константой поверхности kп и механическими характеристиками материала на задаваемом интервале нормальных давлений посредством закона трения (21). Параметры аппроксимации (22) найдем методом Бубнова – Галеркина, находя минимум квадрата невязки по значениям давлений r=τa +f1p-kпτ s[1 - exp (-1,125 p/σ s)] с весом p2 в заданном интервале давлений pmin ≤p≤pmax:

J=∫pmax r2 p2dp → min.

p min

Минимум суммарной невязки J доставляют параметры τa и f1, удовлетворяющие системе уравнений

5=о;

5J

^f 1

= 0.

Исключая из расчетов константу поверхности введением новых переменных

c1 = τa⁄kп ; c2 = f1⁄kп после дифференцирования получаем следующую систему:

[a][c] = [b], где pmax p2

[a] = ∫pmin [p3

p4] dp; [b]

_∫ p max p min

τ s[1 -exp (-1,125 p/σ s)]p2           c1

[τ s[1-exp (-1,125 p/σ s)]p3] p; [c] = [c2]

После численного интегрирования и нахождения коэффициентов матриц, параметры аппрок-

симации определяем путем решения системы уравнений

[c] = [a]-1[b]; τa = c1kп; f1 = c2kп.

Подстановка в условия равновесия (6) вместо произведения f(p)p линеаризованного закона

τa +f1p с последующим повторением выкладок приводит к оценке осевого напряжения

P/F = P/(2πRH) =σφ =σd +σa, где в случае использования закона степенного упрочнения (18)

2 φ′

R (sinf₁φ+f₁ cos f₁φ) exp f₁φ′ - f₁

H τa              1+ f12

σd =K( )m ∫ (ln sec φ)m(f1 + tgφ) exp f1φdφ; σa =

√3   0

В случае если необходимо учесть влияние изгиба на величину усилия, в выражении (23) сле- дует сделать поправку на ∆σφ:

P/F = σφ =σd +σa + ∆σφ,                                                            (24)

где ∆σφ = Mφ – поправка на изгиб [6]. Здесь изгибающий момент Mφ следует определять, вводя в RH рассмотрение некоторое условие текучести.

Экспериментальная проверка . Для установления применимости предложенной методики были произведены испытания на шести образцах – трубных заготовках (R/H = 7,5), две из которых затем были отбракованы. В испытаниях использовался двухканальный преобразователь, который фиксировал сигнал с оптического измерителя зазора между полуматрицами и манометра, подсоединенного к гидросистеме пресса. Результат записывался в виде осциллограмм.

По данным калибровочных осциллограмм был произведен пересчет полученных результатов в виде характеристик давления в гидросистеме пресса для первого перехода формования (рис. 6). Характеристики представлены в координатах «полезное» давление – перемещение поршня.

Под полезным здесь понимается разница между давлением в гидросистеме p _гс и давлением холостого хода p_хх использованного пресса. Для пересчета давлений в усилия приводим площадь поршня пресса со стороны выталкивателя F_п = 0,125 м².

Методом наименьших квадратичных отклонений определены значения констант поверхности в каждом из четырех опытов первого перехода. Матожидание значений констант поверхности составило 〈k_п〉 = 0,302, что соответствует верхней оценке коэффициента трения, равной f = 0,197. Среднеквадратическое отклонение констант поверхности состави л о σ_kп = 0,018.

Соответствующие экспериментам законы трения имеют вид:

τ = 91,0[1 - exp(-p/462)], МПа – при представлении в форме А.Н. Леванова;

τ = 3,07 + 0,146p, МПа – при линеаризованном представлении.

Рис. 6. Характеристика давления в гидросистеме пресса в процессе первого перехода

На рис. 6 показаны экспериментальные характеристики, а также расчет МКЭ для верхней оценки fp сопротивления по Амонтону и теоретическая хара к теристика (23) с границами объективного разброса константы поверхности (доверительная вероятность 99,73 % ). Соответствующий эксперименту закон трения показан на рис. 7. Средняя ско р ость относительного перемещения полуматриц в процессе формования состави л а 19 мм/c.

Заключение. Получено аналитическое решение задачи о необходимом усилии формообразования шаровых пробок путем обжатия относительно тонких трубчатых заготовок в полусферических матрицах. Достоверность решения подтверждена конечно-элементным расчетом и экспериментально. На примере загото- вок из стали 12Х18Н10Т продемонстрирована возможность практического применения решения для экспериментальной оценки параметров трения. Дальнейшие исследования направлены на выяснение причин неустойчивости процесса формоизменения и определения мер, полностью исключающих вероятность возникновения брака.