Аналитическое решение задачи о сходящейся ударной волне в газе в одномерном случае

Развитие теории размерности и подобия величин механики сплошной среды позволило в разные годы ХХ века получить автомодельные решения задачи о фокусировке ударной волны в бесконечном идеальном газе [1–9]. Задачи, имеющие аналитическое решение, еще называют «эталонными» задачами, так как они используются для верификации математических моделей динамических процессов механики сплошных сред. Однако реальные тела имеют конечные размеры. В данной работе рассмотрена задача о сходящейся ударной волне в сосуде с непроницаемой стенкой, имеющая точное аналитическое решение, описывающее три типа одномерных движений – плоские, цилиндрически и сферически симметричные движения.

Постановка задачи

Рассматривается сосуд с непроницаемой стенкой, в котором находится газ массой M ₀ и начальными при t = t 0 параметрами газа р 0 = const, U 0 = 0, P 0 = 0, E 0 = 0, где р - плотность, U -скорость, P – давление, E – удельная внутренняя энергия. Лагранжевой координатой является масса M . Второй независимой переменной является время t . В точке t ₀ , M ₀ задана скорость U 1 <  0. Таким образом, в этой точке задан сильный разрыв, который при t >  t ₀ распространяется к центру симметрии и в момент t f фокусируется в точку M = 0. Граница сосуда при t >  t ₀ движется в переменных r , t , но в переменных M , t её траектория является вертикальной линией. Вообще говоря, все траектории частиц являются вертикальными линиями, вдоль которых сохраняется то значение энтропии, которое возникло на ударной волне. Параметры газа между ударной волной и границей определяются системой законов сохранения Эйлера–Гельмгольца. Уравнение состояния используются в двух формах:

P = ( y - 1 ) p E , P = F ( s ) p ^Y ,

где F ( s ) - функция от энтропии.

Ударная волна

Законы сохранения на ударной волне (УВ) при U 0 = 0, P 0 = 0, E 0 = 0, F 0 = 0 имеют вид [10]:

Pw (D - Uw)- Р0D = 0,(2)

P0DUw - Pw = 0,(3)

P0 D ^ Ew + 2 UW j - PwUw = 0.(4)

Индексом « w » обозначены величины на ударной волне, D – скорость ударной волны. Преобразуем эти уравнения к виду, содержащему зависимости Uw, pw, Fw, Pw от скорости ударной волны в лагранжевых координатах. Лагранжева координата M w ударной волны в одномерном случае связана с её эйлеровой координатой rw уравнением где Ц =«

• 1,    плоская симметрия

• 2,    цилиндрическая симметрия, 8 ц

• 3,    сферическая симметрия

M w = ' " p, г ^Ц , Ц

'1, при Ц = 1

, = <  2 п , при ц = 2.

4 п , при ц = 3

Скорость ударной волны в лагранжевых координатах есть изменение M _w со временем

W = dM f = ^S m P 0 Ц D.

dt

Заменим эйлерову координату ударной волны её лагранжевой координатой. Для этого выразим r_w из (5) и подставим в (6)

W = ( Ц M w ) ^{( Ц - 1)/ Ц} ( S.. P f ^Ц D .

Выразив в (7) D через W и Mw и подставив в (2)–(4), получим с помощью (1) величины на ударной волне, содержащие W и M w :

Y + 1

P w =м P 0 ;

U w = Л ( ^s p ) ¹ “ ( ц M w )" ^{Ц 1 Ц} w ;

Y + 1

P w = —p р 0 ^{Ц - 2 )}/%-2/ ^Ц ( Ц M w ) ^{2 ( 1 - Ц )Z Ц} W 2 .

Y + 1

Из (1), (8) и (10) следует выражение для F_w

F w

у

² I Z z ! I      ( Y ^{- (} Ц ^{- 2} )/ ц ) „ -2/ Ц

Y + 1 1 Y + 1 J ^Р 0         ^{$ Ц}

( ц M w ) ^{2 ( 1 - Ц )/ Ц} W ².

В точке t = 1 0 M w = M 0 , U w = U w 0 , P w = P w 0 , F w = F w 0 выражения (9)-(11) принимают вид:

U w

= U 0

I W I

I W 0 j

(м ^{( Ц - 1)/ Ц} M o. |

I M_w ^J

, ^Pw = ^P 0

I W I ² 1 M 0 1 ^{2 ( Ц- 1 ) Ц}

I W 0 ) I M w j

, F w = F 0

| w I ² 1 M 0 1 ^{2 ( Ц - 1 )}/ ^Ц

I W 0 j I M w ^J

. (12)

По аналогии с [11, 12] зададим траекторию ударной волны в виде

M w = M 0 ^ ( t ) n ,                                  (13)

где ф = ( t f - 1 )Д t f - 1 ₀ ) . Продифференцировав M_w по t , получим выражение для скорости ударной волны в лагранжевых координатах

Механика

W = W ₀ ф - 1 ,

где

W 0 =- - M 0 n_ t f ^- t 0

.

Исключив в (13) и (14) функцию от времени, получим зависимость W от M_w

W

W 0

(м )^{( П-1)п}

M w

I Mo J

.

С помощью соотношения (16) исключим W в (12):

U w = U w 0

(ад А^{( П - д )}/ Ц ^П

w I

Л/f I , Pw   Pw 0

к ^_ 0 V

r

к

M

M

- I2(n- ц)/ цп w|       , Fw = Fw 0

А^{2( П -} Ц )! ^{Ц П} M w I к _ 0 V

.

Поскольку M_w и t связаны уравнением траектории ударной волны, то из (13) и (17) следуют зависимости U_w , P_w , F_w от t :

ТТ — ТТ _fn ( ^{п ц} )/ ^ц р — р 2А^{п ц)}1^ц р — Р 2А^{п ц})/^ц U w = U w 0 Ф     , P w = P w 0 Ф , F w = F w 0 Ф      .

Величина F_w вдоль траектории частицы с координатой M_w постоянна. Следовательно, зависимость энтропии от массы между ударной волной и границей газа имеет вид

г

F = F w 0

к

_ | 2 ( n -ц )/ ц п

_ V

.

Из (5) следует зависимость rw от Mw rw = -0

(М 1Ц к _ 0 V

.

Выбор траектории УВ в форме (13) определяет характер зависимостей W и D от M_w . При n <  1 W ^ -~ , если __w ^ 0, при n = 1 W = W ₀ = const и при n >  1 уменьшается при уменьшении M_w . Эти типы зависимостей приведены на рис. 1. Зависимость D от M_w следует из (7) и (20)

D

D 0

Из (21) следует, что при n < ц D ^-'

г

к

M

M

- \ ( n - ц )/ цп w

.

^ , если M w ^ 0, при n = ц D = D 0 = const и при

n > ц D ^ 0 при уменьшении __w (рис. 2). Фактическая реализация одного из этих режимов возможна лишь при организации соответствующего течения газа между фронтом УВ и наружной границей.

Течение газа за ударной волной

Параметры адиабатического течения за ударной волной определяются уравнениями, траектории, сохранения массы и движения:

Id- I - U = 0,                                    (22) к d t V _ ( др I           д( - ц - 1 и ) кd t V _ + s*p d _ "°’                         <23) Г W 1 + s,-»--^ = 0.                   (24) к d t V _    ц      д _                                  ’

Эти уравнения содержат три искомых функции r , р и U . Величина F определяется на ударной волне и зависит только от M (17).

Перейдём в (22)-(24) к новым искомым функциям

R = r ^ , C = r ^ ^{- 1} U .                                  (25)

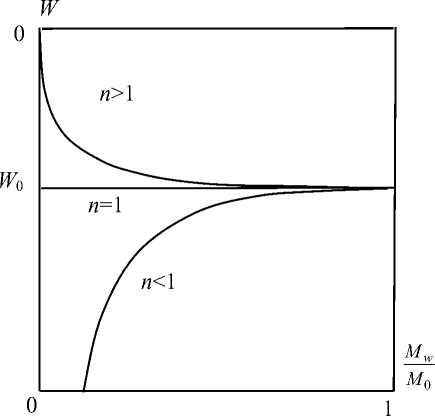
Рис. 1. Схематическое изображение возможных зависимостей W ( M w )

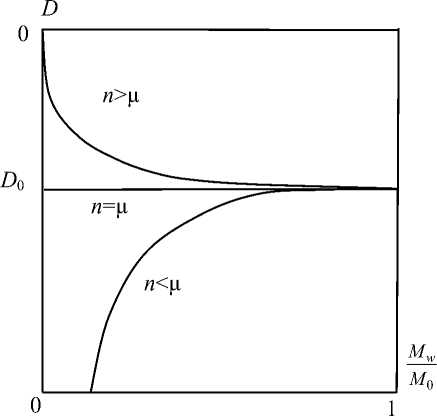
Рис. 2. Схематическое изображение возможных зависимостей D ( M w )

После перехода к функциям R и C уравнения (22)-(24) примут вид:

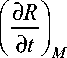
— U C = 0,

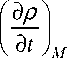
∂ C

+ s. р ---= 0, uP дM

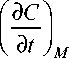
+ s„ R ^{2( u 1)Z u д (} F ^P ) — 2 С ² R ^{1 µ}

= 0.

Из (17), (19) и (25) следуют зависимости R w и C w от M w :

R_w = R w , C_w = С_о w 0 w 0

^M 0

M w к M 0

( n — 1 )/ n

Уравнения (26)-(28) являются основными для отыскания R , С и р в области интегрирования

M w <  M <  M 0 , t 0 <  t <  t f .

Перейдём от переменных t, M к переменным t, !(t, M). С помощью уравнений для произ- водных fд к fд к   fд к fд^к     f д к  fд V д^ к

I I =1 I  +1 I I I ,      I I  = 1 II ^| к дt)m к дt J^  к д^ )t к дt)m    к дM )t  к д^ Jt к дM )t преобразуем уравнения (26)-(28)

( дR )  ГдR V д^ )

+            - uC = 0 , к дt )^ кд^ Jt к дt )m’ f д-Р) + ( др)f д!) + s р2 ( д€ )Г д^ ) = 0

к дt J^ к д! Jt к дt )m   uP к д! Jt кдM Jt’ д C )  f д C )f д! )

1 ⁺ I 11 I ^д t ) ! к ^д! ) t к ^д t ) m

t ^ -y C ² + s„R ² " ^{- 1)/} "

R ^µ

_y f д F к f д! ) ρ ^γ

^P к д! 1 ₁ к д M 1 ₁

+ y F P ^Y -

f др к f д! к к д! J t к д M ¹ ₁

= 0. (32)

Механика

Зависимость £ ( t , M ) зададим так, чтобы на ударной волне было § = 1. Из (13) следует, что проще всего взять такую зависимость в виде

M

§ = ТТ^ .

M ₀

Для разделения переменных представим R , р и C в виде произведений функций от времени на функции от £

R = «R (t)Т(£) р = ар (t)8(%) C = ас (t)Z(£).(34)

Поскольку на ударной волне ^ = 1, то значения Т 1 = Т ( 1 ) , 5 1 = 5 ( 1 ) , Z 1 = Z ( 1 ) должны быть постоянными. Из (29) и (33) следует зависимость R w ( t )

Rw = R0 ^.(35)

Сравнив эту зависимость с (34) на ударной волне, получим выражение для aR aR (t) = Rо ^T-1.(36)

Аналогично для ар и ас получаем соотношения ар = ро f1+1V1,   ас (t ) = Cо ^-1Zf1.(37)

V Y - 1 )

Подставив (34)-(37) в (30)-(32) и воспользовавшись (15), получим три уравнения для Т , 5 и Z :

^Т ' = A1,(38)

51 B1 Z'- $Z 15 = 0,(39)

- ^ ZЧ CY5 C2,(40)

Z1

где штрих означает дифференцирование по £ . Коэффициенты уравнений (38)-(40) A 1 , B 1 , C 1 , C ₂ с помощью (5), (6), (12) и (23) преобразуются к виду

2 zt             2 5 2            5 ' - 1 Т ^{2 ц- 1} ) ^ц ^ ^{(( ц 2 ) и + 2 ц)ц п}

^{A, = Т} . _; - iv - B ¹ " ( Y - i )? ’ ^{C, =}         5' - 1 т 1² < * ^{- 1 )}"

,

C = 2 ( ц - 1 ) Z ² Т ( и - 1 ) Z

² ц ( у + 1 ) Z 12 Т    nZ 1

² ( и ^- ц ) 5

C ₁

Ц и 5 1

.

Уравнения (38)-(40) образуют относительно Т‘, 5, Z' систему линейных неоднородных уравне- ний. Определитель системы равен

А = B 1 C 1 Y; - е.

Если А ^ 0, то решение системы (37)-(39) существует и имеет вид

Т ' = A 1 5 = B 1 ^C 2 ⁵ 1 z ’ = ^ ^C 2 Z 1 ^ ’ А , А

.

Интегрирование системы уравнений (42) начинается в точке ^ = 1 (на ударной волне). Расчёты показывают, что существует промежуток значений n таких, что определитель в ноль не обращается. При некотором значении и* определитель обращается в ноль при ^ = ^*. В этой точке решение существует, если C2 тоже обращается в ноль. Каждому значению у соответствует одно значение и* (таблицу). В этой же таблице приведены значения ^*, при которых одновременно А(^*) = 0, C2(^*) = 0.

В лагранжевых координатах построено аналитическое решение одномерной задачи о сходящейся ударной волне для трех типов симметрии, и для широкого диапазона показателей адиабаты идеального газа найдены соответствующие показатели автомодельности.

Значения n _∗ и ξ _∗ , соответствующие различным значениям показателя адиабаты γ

µ	γ	1,1	1,2	4/3	1,4	5/3
1	n ∗	1,0	1,0	1,0	1,0	1,0
	ξ ∗	4,691312	3,464715	2,828906	2,646222	2,236450
2	n ∗	1,770501	1,722331	1,684516	1,670651	1,631252
	ξ ∗	6,768540	4,873946	3,896265	3,616019	2,990161
3	n ∗	2,387916	2,271434	2,183068	2,151532	2,065135
	ξ ∗	7,959997	5,717071	4,559431	4,227062	3,481885

Статья выполнена при поддержке Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.А03.21.0011.