Аналитическое решение задачи о течении газа в профилированном капилляре с вибрацией его стенок

Введение. Пневматическое сопротивление типа капилляр является простейшим элементом пневмоавтоматики, характер течения газа в котором в линейном приближении полагают ламинарным, а процесс течения изотермическим. В таких условиях поток газа в капилляре определяется формулой Пуазейля [1]. Обычно формирует поток газа в капилляре перепад внешнего давления, но в качестве альтернативного решения может быть использованы профилирование и вибрация [2] и в этом случае у капилляра появляются компрессорные свойства, оценка которым дана в статье. Решение будем искать, используя хорошо зарекомендовавшую себя асимптотическую теорию вибронесущего газового слоя [4]. Данный аналитический подход предполагает использование бесконечно большой частоты вибрации стенок капилляра, поэтому для сравнительно малых частот результаты исследования имеют приближенный характер, а погрешность решения нуждается в оценке.

Аналитическая модель. На рис. 1 приведено схематическое изображение профилированного капилляра длиной L с входным Г] и выходным г₂ радиусами, где L » и и г₂. Боковые поверхности капилляра совершают колебания с постоянной амплитудой Ну, за счет чего осуществляется высокочастотное периодическое сдавливание газа в капилляре. Функция радиуса капилляра в цилиндрической системе координат имеет вид

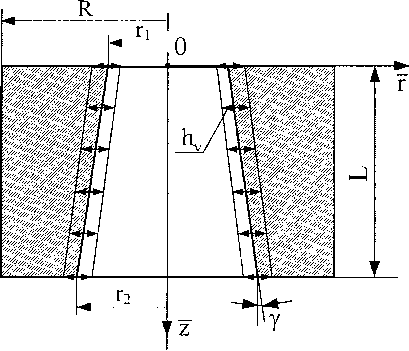
Рис. 1. Профилированный капилляр с вибрацией стенок

h(z, т) = Г] + yz + h_v cos(t),                   (1)

где у - угол наклона боковой поверхности капилляра, формирующий профиль; z - продольная координата (0 < z < L); т = И - безразмерное время; v - циклическая частота колебаний стенок капилляра; t - время.

Допустим, что течение газа в капилляре вдоль оси 0 z с учетом вязкостных слагаемых определяется укороченным уравнением Навье-Стокса, которое в цилиндрической системе координат г, У, z имеет вид ар 1 a L аул — = ц-— г—— az г аг ( аг)

где р - давление в газе, ц - динамический коэффициент вязкости, V^ - проекция скорости частиц газа на ось z . Дополнительно принимаем условие 5р/9г = 0 .

Уравнение неразрывности потока в цилиндрических координатах f^+^(pvfr)+r^(Pv2)=o, at ar az

где р - плотность газа, V_f - проекция скорости частиц газа на ось г .

Интегрируя первое уравнение в (2) дважды и учитывая, что давление не зависит от коорди наты г, получим:

в\-    1 ар_ cj

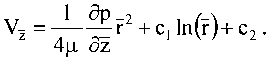
—^ =--_г + ^- аг 2ц az г

Постоянные интегрирования в (4) определяем из граничных условий V- = 0 при г = h и aV^/af = 0 при г = 0 и, следовательно, с^О, с2 = -h2/(4p)dp/dz. Выражение для скорости вдоль оси 0 z примет вид

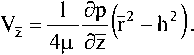
^(ph²) St '

Проинтегрируем (3) по переменной г в пределах от 0 до h с учетом (5): а 1 1 a(ph²)² (ph²)² ан² ж 8ц ^2 5z н² az

Перепишем (6) в безразмерном виде, введя безразмерные величины

Р = р/Ра, z = z/L, Н = ЬД ,т = vt и вспомогательную функцию Т = РН2:

5 i st² t² эн² __Л ат

3z 2 dz Н2 3z v дт ’ где Av = 8цЬ2у/ц2Ра) - безразмерный частотный параметр, Ра - атмосферное давление, Н = Но +Htcos(t) - безразмерная функция зазора, где Нт = hv/r1, Но =l + konz, kon =tg(Y)L/r,.

Отметим, что вспомогательная функция давления для капилляра равна произведению давления на квадрат функции зазора, что отличает ее от вида функции давления, вводимой для обычных вибронесущих смазочных слоев. Идея использования такой функции в асимптотическом анализе капилляра выдвинута совместно с С.Г. Некрасовым и ее асимптотический характер подтвержден в результате численного эксперимента. Применяя асимптотическую теорию [4], введем не зависящую от времени функцию давления Т_ю, соответствующую условию X_v ^ оо. Проинтегрируем (7) по безразмерному времени т в пределах от 0 до 2тг и после преобразований получим осредненное за период колебаний уравнение для распределения давлений

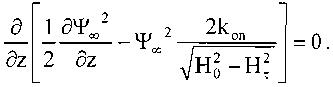
Асимптотические граничные условия аналогичны условиям в работе [4]: ^(z = 0) = H^(z) + |h^+3H²(z)H²] ;

(Ю)

^tP²(z = l) = K² H^(z) + |h^+3H²(z)H²   ,

L о                 Jz=i где Kp - отношение давлений на выходе z = 1 и входе z = 0 капилляра.

Паш ни на К. А.

Асимптотическая краевая задача (8)—(10) является линейной и позволяет получить аналитическое решение для вспомогательной функции ФооВ виде

■2

Н^

lt(l)lt(O)[fp(l) + sp(l)-fp(O)-sp(O)]

rt(l)lt(O)Kp-lt(l)rt(O) rr_/v

(И)

lt(l)lt(o)[fp(o) + sp(o)-fp(l)-sp(1)j

Л4                                                 3

; lt(l) = lt(z = 1); Zz(O) = Z/(z = O); rt(z) = H⁴(z) + -H⁴ + 3H²(z)H7

/                                                           8

Hq - H^ ; fp(l) = fp(z = 1);

rt(l) = rt(z = 1); rt(O) = rt(z = 0); fp(z) = -4(Hq

120Hq

10H^-konz

fp(0) = fp(z = 0); sp(z) = konz

-Н2 120 Н;

•2 кри^ ° ₃

(2konz + 3) -15Н?

sp(l) = sp(z = 1); sp(o) = sp(z = О).

Среднее за период колебаний избыточное давление в капилляре:

Hq       l гШ-Н!

Средний за период массовый поток в направлении оси z имеет вид

М=-2лКг            2к°"    ,

2 dz /и? -И2

где Кг = paPar14/(16pL).

Выражение (13) для непрофилированного капилляра коП = 0 с вибрацией Нт тЮ и профилированного капилляра коП тЮ без вибрации Нт = 0 имеет вид

—      ( 3

М=-лКг 1 + -

Ч 8

H?+3H² (к^-1) и М=-лК_г

з+зкоп+кЧ

При внешнем перепаде давлений и отсутствии профилирования и вибрации выражения для потока газа в капилляре (14) сводятся к известной формуле Пуазейля [1]:

M=^feL_

256pLRT

p

16pL

Сравнение результатов. Численная модель течения газа в профилированном капилляре с вибрацией построена при использовании метода, изложенного в [3]. Решение заключается в линеаризации модели (7) с использованием метода Ньютона-Канторовича, построении системы разностных итерационных уравнений с использованием интегро-интерполяционного метода. Решение полученной в результате алгебраической задачи на каждой итерации проводится методом исключения Гаусса до выполнения условия итерационной сходимости. Для получения решения обеспечивается установление переходного процесса при выполнении условия периодичности для искомой функции давления.

Сравним результаты средних за период потоков, полученных на основе асимптотического и численного решений. Зависимость безразмерного среднего за период потока от параметра профиля капилляра (рис. 2) практически линейна при значениях частотного параметра Лг больших 10, но при его уменьшении зависимость потока становится нелинейной и при малых значениях частотного параметра профиль практически перестает оказывать влияние на поток. При значении частотного параметра равного 150, зависимость потока приближается к асимптотической зависимости (13) при Лv -^ оо

Зависимость среднего за период потока от амплитуды колебаний (рис. 3) нелинейна и с увеличением амплитуды поток значительно возрастает, что справедливо для всех рассмотренных параметров профиля капилляра. Так же, как и ранее, при значении частотного параметра равного 150, зависимость потока приближается к асимптотической зависимости (13) при Лг -^ оо

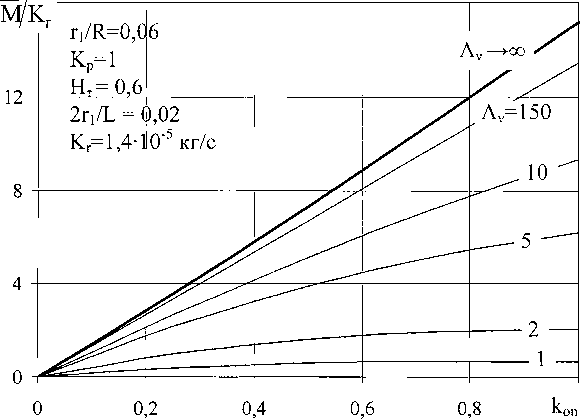
Рис. 2. Средний за период поток газа в капилляре в зависимости от параметра профиля kon

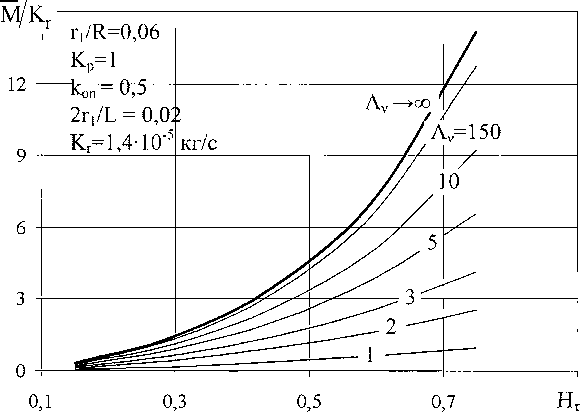
Рис. 3. Средний за период поток газа в капилляре в зависимости от амплитуды Нт

Выводы. Впервые построена аналитическая модель течения газа в профилированном капилляре с вибрацией его стенок и получено аналитическое решение для функции давления и потока газа. Решение было бы невозможно без введения новой в теории вибронесущего тонкого слоя асимптотической функции давления.

Рассмотрены частные решения и показано, что без вибрации выражение для потока газа совпадает с известной формулой Пуазейля.

Наличие потока газа (13) без приложенного по краям слоя внешнего перепада давлений говорит о наличии компрессорных свойств капилляра. Из рис. 2 и 3 видно, что возможно достижение значений расходов порядка 103 кг/с и больших при увеличении амплитуды колебаний.

Отметим, что аналитическое решение, полученное при использовании асимптотического приближения задачи, дает лишь оценочное решение для малых (реальных) значений частотного

Пашнина Н.А.                                 Аналитическое решение задачи о течении газав профилированном капилляре с вибрацией его стенок параметра. Поэтому полученные аналитические решения (13) или частные случаи (14) можно использовать для предварительной оценки значений потока газа, генерируемого профилированным капилляром с вибрацией, которые следует уточнять.