Аналитическое решение задачи по расчету температурного поля в обрабатываемых заготовках при ленточном шлифовании

В современном высокотехнологичном машиностроительном производстве значительное внимание уделяется качеству обработки и, в частности, состоянию поверхностного слоя, определяемого глубиной и степенью наклепа (разупрочнения), величиной и знаком остаточных напряжений, структурой и фазовым состоянием обрабатываемого материала и т.д. На формирование поверхностного слоя в наибольшей степени оказывают влияние финишные операции, к которым относятся процессы шлифования, в том числе и ленточного [1- 8].

Тепловые явления, сопровождающие процессы ленточного шлифования, при определенных условиях формообразования поверхности могут оказывать решающее влияние как на качество обработки, так и на износостойкость режущего инструмента. Особую роль тепловые процессы приобретают при обработке материалов склонных к возникновению шлифовочных прижогов и трещин, в частности, высокоуглеродистых, цементируемых и высокопрочных сталей, титановых сплавов [1, 3-8]. Повышение среднеконтактной температуры в зоне обработки выше 500 ^оС при шлифовании титановых сплавов приводит к росту β - фазы, что недопустимо техническими требованиями на операцию при изготовлении высоконагруженных деталей [1, 10, 11], например, лопаток компрессора газотурбинных двигателей. Поэтому рас-

чет температурных полей в зоне резания при шлифовании абразивными лентами различных типов: сплошными, прерывистыми, композиционными, содержащими участки с абразивными зернами и твердой смазкой, комбинированными, содержащими участки заполненные и не заполненные абразивными зернами, и участки с твердой смазкой, представляет большой практический интерес. Однако для определения температурных полей необходимо наличие аналитических зависимостей и на их базе соответствующей методики, позволяющей технологу выполнить расчет и сделать заключение о возможности возникновения структурных и фазовых превращений.

МЕТОДИКА

Как известно, процесс обработки профиля пера лопаток компрессора и турбины на ленточно-шлифовальных станках с ЧПУ осуществляется методом строчного шлифования, причем как в направлении вдоль пера лопатки, так и в поперечном направлении, т.е. вдоль сечения профиля. Данные две схемы обработки при определенных допущениях можно привести к единой – поперечной. Кроме того, результаты расчетов, выполненные по методике, приведенной в работе [7], позволили констатировать, что если характерный размер обрабатываемой заготовки много больше глубины прогрева, равной примерно 0,3 мм поверхностного слоя, то тело произвольной формы без существенной погрешности можно рассматривать как полуогра-ниченное тело, т.е. тело ограниченное “плоскостью”, на которой действует тепловой источник или осуществляется конвективный теплообмен в соответствии с условиями ленточного шлифования. Поэтому решение задачи по определению температурного поля в заготовках при шлифовании абразивными лентами различных типов, с учетом конвективного теплообмена обрабатываемой поверхности с охлаждающей жидкостью вне зоны контакта ленты с заготовкой, может быть сведено к решению задачи по расчету температурного поля в заготовках при плоском шлифовании комбинированной лентой. Схема плоского шлифования комбинированной абразивной лентой приведена на рис. 1. Как уже отмечалось ранее, комбинированная лента включает участки, присущие лентам различных типов, поэтому решение задачи по расчету температурного поля в заготовке при ее шлифовании сплошной, прерывистой и композиционной лентами может рассматриваться как частный случай решения задачи по определению температурного поля при шлифовании комбинированной лентой.

Для создания модели ленточного шлифования в качестве прототипа применялась модель для расчета температурного поля в обрабатываемых заготовках при шлифовании их кругами различных конструкций, приведенная в работах [1, 9].

При постановке и решении задачи по расчету температурного поля в заготовке при плоском шлифовании комбинированной лентой, с учетом конвективного теплообмена обрабатываемой поверхности с охлаждающей жидкостью вне зоны контакта шлифовальной ленты с заготовкой, на основании изложенного ранее и анализа результатов теоретических и экспериментальных исследований были сделаны следующие допущения:

• -    тепловой источник имеет полосовую форму и бесконечную ширину (задача двухмерная) и непрерывно действует в течение контакта режущего участка ленты с заготовкой. Интенсивность источника равномерна по всей площади контакта и постоянна во времени, источник движется по поверхности тела со скоростью и _з ;

• -    влияние теплопереноса в направлении поперечной подачи пренебрежимо мало;

• -    теплофизические параметры обрабатываемого материала и смазывающе-охлаждающих участков ленты считать постоянными;

• -    температура охлаждающей жидкости остается постоянной, равной температуре окружающей среды.

С учетом принятых допущений, задача формулируется следующим образом. По поверхности полуограниченного тела (заготовки) в направлении, противоположном направлению движения заготовки со скоростью и _з , движется прерывистый полосовой тепловой источник с плотностью теплового потока, равной q . Характерной особенностью процесса шлифования является то, что направление теплового потока в зоне контакта ленты с заготовкой периодически изменяется. Тепловой поток направлен то в обрабатываемую заготовку, то из неё. На вне-контактном участке комбинированной ленты с заготовкой и во время прохождения участками ленты без зерен зоны контакта происходит конвективный теплообмен обрабатываемой поверхности заготовки с охлаждающей жидкостью с коэффициентом теплоотдачи а _сож , а во время контакта участков ленты с твердой смазкой

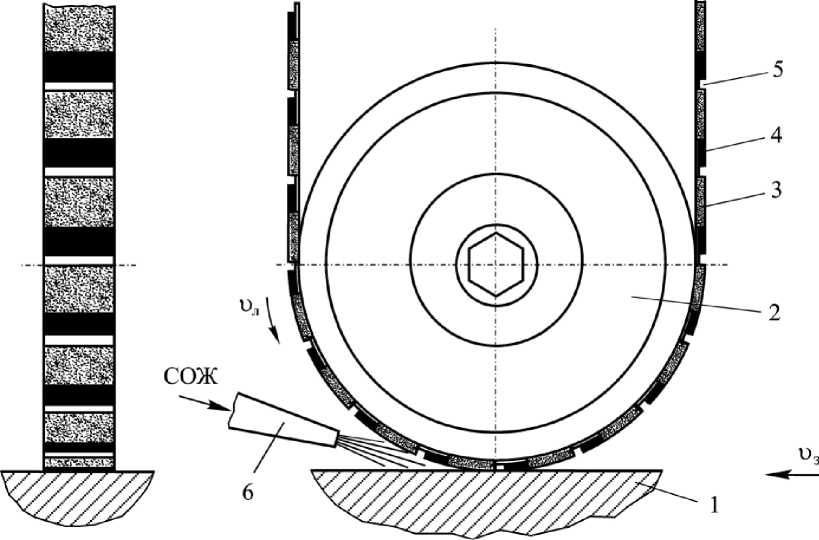
Рис. 1. Схема плоского шлифования комбинированной лентой:

1 – обрабатываемая заготовка; 2 – прижимной ролик; 3 – участок ленты с абразивными зернами;

4 – участок ленты с твердой смазкой; 5 – участок ленты без абразивных зерен; 6 – сопло для подачи СОЖ

с поверхностью заготовки происходит перенос тепла с обрабатываемой поверхности в твердую смазку с коэффициентом теплоотдачи а _тс . Следует определить распределение температуры на поверхности и внутри заготовки.

Схемы распределения тепловых потоков на поверхности тела во время работы комбинированной шлифовальной лентой представлены на рис. 2.

Математическая модель теплообмена при ленточном шлифовании представляет собой краевую задачу для двухмерного нестационарного уравнения теплопроводности в движущейся системе координат:

д Т = ( д ² Т д ² Т ) - д Т д t _v д x ² д у ² _v ^з д x ’

• -те < x < те;

о <  у; о <  t ,                ⁽¹⁾

где T = Т ( t, x, у ) - температура, К; t - время, с; x , у - текущие значения координат, м; a - коэффициент температуропроводности материала заготовки, м²/с; з - - скорость движения заготовки, м/с.

По условию задачи теплообмен происходит в полупространстве -те <  x < те , у > 0 для моментов времени t > 0 . Граничные и начальные условия для уравнения (1) имеют вид: граничные условия:

• = b ⁽ x , t^{)(Т - т} те )| y =₀ + d ⁽ x , t ) при t >  0 , (2) у = 0

  . д Т л-- д у

  
  

начальные условия: Т (0, x, у ) = Т ₀ = Т _те , (3) где Л - коэффициент теплопроводности материала заготовки, Вт/(м*К); Т ~ - температура окружающей среды, К.

Значения функций b ( x , t ) и d ( x, t ) приведены на рис. 3 и определяются применяемым видом ленты. Причем зависимость от t носит периодический характер с периодом Т_ц .

Период цикла определяется по формуле:

1 =------= 1    +1    +1- , ц                     У4• рз     уч• тс     уч•бз 7

”рол N где 1ц - время цикла, с; прол - число оборотов прижимного ролика, об/мин; N - число участков на длине окружности прижимного ролика, на которых не производится процесс резания, шт.; 1учрз, t - время контакта, соответственно, участков уч.тс с режущими зернами и твердой смазкой с обрабатываемой заготовкой, с; t   - время прохож- уч.бз дения участком ленты без зерен зоны контакта её с заготовкой, с.

В случае если t = 0. t = = 0. t ^ 0, уч • тс        ‘ уч • бз        ‘ уч • рз задача расчета температурного поля в заготовке при шлифовании комбинированной лентой сводится к задаче по определению температурного поля в заготовке при шлифовании сплош-

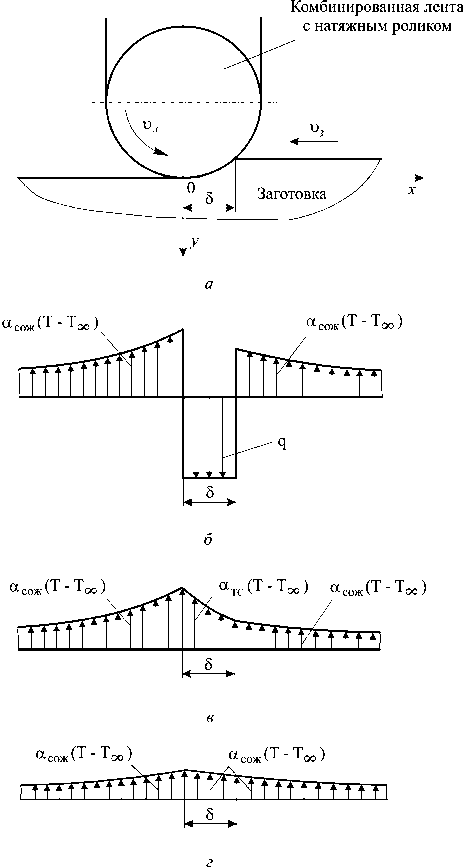
Рис. 2. Схемы ленточного шлифования ( а ) и распределения тепловых потоков на обрабатываемой поверхности заготовки во время прохождения зоны контакта участками ленты с абразивными зернами ( б), с твердой смазкой ( в ) и без абразивных зерен ( г )

ной лентой. Если t _уч ^ _бз ^ 0 , t _уч ^ _рз ^ 0 , задача расчета температурного поля в заготовке при шлифовании комбинированной лентой, соответственно, сводится к задаче по определению температурного поля в заготовке при шлифовании прерывистой лентой, т.е. с участками без абразивных зерен и т.д.

Сделаем замену переменных Т - Т₀ ^ Т . В этом случае исходное уравнение изменений не претерпит, а граничные и начальные условия упростятся:

= b ( x, t ) Т | =₀ + d ( x, t ) при -те< x <те , (4) у =0

_Л д Т ду

Т ( 0, x, у ) = 0.

Произведем преобразование Лапласа функции T по переменной у :

1ц ty4-p3F tmc + t y4 ^3

^уч.рз + tmc

Участок без режущих зерен

Ь СС_Сож? ^ О

Конвективный теплообмен b = оссож; d = 0 1уч.рз

Участок с твердой смазкой b ^{= a}mc \ d О

Конвективный теплообмен b — схС0Ж, d — О

О

Участок с режущими зернами b = 0; d = -q

х

Рис. 3. Схема для определения значений функций b ( x , t ) и d ( x , t )

да

T V ⁽ t , x , u ) = J T ( t , x , y ) exp(— uy ) dy .

Здесь и далее индексы V , т , х , означают, что мы имеем дело с лапласовскими (или Фурье) образами по переменным y , t , x , соответственно.

Уравнение (1) при этом примет вид:

( д2T         Л     дT pTTT — а I -my- + u Ttt l + u( -T" = J^( x — x)FT (p, x, u) dx , l дx          )      дx J

где

T = a д t

^{д T}V ,                     5 T

—у + u T V ^— uT ( t , x ^,0 )--— д x                    д y

y = 0 7

д T , ^— и -F . (6) d x

да

F_T ( p , x ', u ) = J exp(— pt ) F ( t , x ‘, u ) dt .

Введем функцию Грина G _vt в смешанном представлении, подчиняющуюся уравнению:

Решение уравнения (6) будем искать методом функций Грина. Для этого представим его в виде:

PGV T - a

dS G T¹ " + u ² G" д x

+ и ^ G V" = ^ ( x — x ') .

^f д x

d T

—- — a д t

2т .

-4 ^T + u²T_v 1 + и ^ T- = а — uTU , x ,0) д x ^{2 V}) ^? d x             ⁽ )

d T 5 y

где

= J £ ( x — x ' ) F ( t , x',u ) dx ',

F ( t ,x,u ) = a

— u

—

d T 6 y

. (8)

Подставляя граничные условия (4) в соотношение (8), получим:

Применяя преобразование Лапласа по переменной t

да

Tvt (P , x, u) = J TV (t, x, u) exp(—pt) dt к уравнению (7) с учетом начальных условий (5), приходим к следующему уравнению:

Фурье-образ этого уравнения имеет следующий вид:

pGTTx — а (— к2 Gvtx + u2 GVTX ) — ikUeGvTZ = exp(ikx') , откуда следует, что

^Gvt% ⁽ p , ^k , u ) =

exp( ikx ')

p + а ( к¹ — u¹ ) — ik o_Q

Переходя от лапласовских и Фурье-образов к оригиналам и применяя теорему о конволюции, представим решение исходной задачи в виде

1 c + i да                         i да

T ( t , x , y ) =--- [ du exp ( uy )— Г dk exp ( — ikx ) •

2ni             2п к c—i да                            —да

да

t

• J dx' exp ( ikx ') J d - F ( t — t , x\u ) ^ ( - ) =

—да

¹ l l,' n     ( x ^,— x ^— u ^t )

= — d - dx J — exp — ------—^L

2.П ' _—¹     V а т             4 а т

—да

•

1 c + i да

---; J du exp ( uy ) F ( t — - , x ', u ) exp ( а - u ²) ,

^П‘ c — i да

где

i а + i да

^(r) = — J dp 2лг < а - i да exp( pr)

p + a ( k ² - u ²)- iku ^

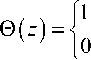
при при

z >  0

z <  0

= exp [-( a ( k ² - u ²) + iku _g ) r J .

Представим последний интеграл в формуле (9) в следующем виде:

1 c + i да

П^ J du exp ( uy ) F ( t , x , u ) exp ( a r u ² ) =

c + i да

=-- ; j du exp ( uy ) exp ( ar u ²) ■ [ ( u + x b ( x , t ) ) ■ T ( t , x ,0 ) + x d ( x , t

М Л

Вторая функция граничных условий для вышеуказанной шлифовальной ленты также представляет собой линейную комбинацию функций Хевисайда:

b ( x, t ) = а _сож 0 ( - x ) + а _сож 0 ( x - S ) +

+ a _Tc © ⁽ 5 ^- x ⁾ 0 ⁽ x ^ 0 ⁽ nt , ⁺ t _y4 p₃ ⁺ t ₇₄„_c ^- t ⁾ 0 ⁽ t ^- nt , ^- t „. p, ^{) +} n = 0

+ «сож 0(S - x)0( x )Ё 0( ( n + 0 t, - t ) 0( t - nt, - tуч.рз - t„^c ) > n=0

где

= - a

d

— + X 'b ( x , t ) I T ( t , x ,0 ) + X d ( x , t ) ■ ф ( y )

,

1 c + i да

ф ( y ) =--- I du exp( uy )exp( a r u ²).

2ni J c -1 да

При помощи замены переменных этот интеграл легко вычисляется:

1 c + i да

ф ( y ) = —; J du exp( uy ) exp [ aru ² J =

-

u = ^

(15) где а _сож - коэффициент теплоотдачи между шлифуемой поверхностью заготовки и СОЖ, Вт/ (м²*К); а _тс - коэффициент теплоотдачи в зоне контакта обрабатываемой поверхности заготовки с твердой смазкой, Вт/(м²^К).

В зоне контакта ленты с обрабатываемой поверхностью заготовки можно пренебречь влиянием теплообмена на характер распределения температуры и в нулевом приближении считать, что тепло от шлифуемой поверхности

i да

= — J d^ exp( i^y ) exp ^[ - ar^ ^] = ^{2 П} --да

-

y ²

4 ar

.

Подставляя выражение (10) в формулу (9),

приходим к следующему выражению для поля температур в шлифуемой заготовке:

tf ^да

T ( t , x , y ) = —j —J dx I—— A b ( x , t - r ) T ( t - r , x ,0 ) - X d ( x , t - r ) I ■

4n„r^J \ 2 a r                                                J

0 -да L x                                                                        / J

■ exp

( x ' - x - u _f r ) 2 + y y 4 a r

отводится только за счет теплопроводности металла. Поэтому интегральное уравнение (12)

допускает решение методом последовательных

приближений:

1 t д да

T ⁰ ( t , x ,0 ) =--j— j dx'd ( x ', t - r ) exp

4 nX „ r ¹

0 -да

= —— [— f ( t - r ) f dx' exp 4 nX ^J r ^{(    )J P}

( x ' - x - u , r ) ² 4 a r

( x'- x ^{- u} , ^r ) 2 4 a r

t 7                 5 - x -u ₍ r

= 4 q 2 h^ f ⁽ t - ^T ) J dx' exp

^{4 nX} 0 ^r            - x -u _c r

( x ') ²

4 a r

причем температурное поле на поверхности детали T(t, x,0) удовлетворяет интегральному уравнению:

т (t, x ,0) = —Ltd! ■ (     )    4nX J r да

■ J dx '[ b ( x ', t - r ) T ( t - r , x ' ,0 ) + d ( x ', t - r ) J exp

-да

( ^x '- ^{x - u} _t ^r ) ²

4 a r

Для определенности рассмотрим, например, процесс теплообмена для комбинированной шлифовальной ленты, имеющей длину зоны контакта с заготовкой, равной 5 . В этом случае:

d ( x , t ) = - q ■ f ( t ) ■© ( £ - x ) ■© ( x ) , (13)

где

TO f (t) = £ 0(nt, + ty4.p3 - t) 0(t- nt4). (14) n=0

В формулах (13) и (14): q - плотность теплового потока, Вт/м²; 0 ( z ) - ступенчатая функция Хевисайда:

= Ba'id r f ( t - , ) 2 _nX

^{5 -} x ^-u < ^r

2 V a r

J d ^ exp ^[- ^ ² ] .

- x -u . r

2 V a r

Окончательное выражение для температуры поверхности обрабатываемой заготовки

T ⁰ ( t , x ,0) имеет вид (определение интеграла ошибок см. в [12]):

т ^,0,( t , x ,0) = q- 4 X

^{f (} t ^{- r} )

.

Температурное поле внутри детали в нулевом приближении вычисляется совершенно аналогично на основе соотношения (11):

т ⁽⁰⁾( t , x , y ) = q J a ■

4X V п rdr        y2       z-f5-x-urда     jx+urда ...    .

■ J -i=exp --— ■ erf I —X+r=^ 1 + erf | „ Л I ‘ f ( t - r ) 0 V r L 4 a r J ^ V 2V a r у     V 2y a r yJ

В следующем приближении по параметру малости задачи теплоотвод осуществляется не только за счет теплопроводности металла, но и за счет теплового контакта заготовки со смазывающе-охлаждающей жидкостью (в зоне контакта и за ее пределами) и твердой смазкой (в зоне контакта). Учитывая это и подставляя решение нулевого приближения (16) в соотношение (11), получим выражение для поля температур в заготовке, шлифуемой комбинированной лентой:

T ⁽¹⁾( t , x , y ) = T ⁽⁰⁾( t , x , y ) +

M

f(A = V©(nt+t + t -t] &(t-nt -t ), (21)

d 1 \ /    / J \ ц уч. рз уч. тс /     \ ц уч. рз /, х / n—0

м fA t) — £ О(( n + 1) Ц - t ) ®( t - nt, - tуч. рз - t уч. тс ) . (22) n—0

Поэтому в указанном приближении поправка первого порядка к температуре поверхности заготовки принимает вид:

1 dT

A Т ⁽¹ ( t ^, x ^,0 ) = - —J — (^атсf l ( t ^{- т} ) ⁺ « сож f • ( t ^{- т} ) ) ■

ПЛ 0 т

— — dx

4n^j„ t ¹ 0     -*

—— 2 ¹ b ( x ', t - t ) t ^{( 0 )}( t - t , x ',0 ) • 2 ат ^v ’ ^v ’

• J dx ' • T ⁽⁰⁾ ( t - т , x ' ,0 ) exp

( x '- x ^- и , ! ) ² 4 а т

• exp

( x - x - uy ) + y

4 а т

Подставляя (16) в (23) приходим к окончательному выражению для A T ⁽¹⁾( t , x ,0):

^A T ^(,)( t ^, x ^,0 ) = - 1^ П_ _ ^ . j d l ( « тс f l ( t ^-T ) + а _СО ж f _: ( t ^-T ) ) ■

Очевидно, что в этом приближении темпе-

ратура поверхности заготовки равна: T ^{( 1 )}( t , x ,0 ) = T ( t , x ,0 ) -

t f ^T d S H

•^J > ^{z (} t ^{- т -} " ) •

1 t я *

--j— J" dx'b ( x ', t - т ) T ^{( 0 )}( t - t , x ',0 ) exp

^{4 n}^ 0 ^t -*

-

( x '- x ^- uy ) ² 4 а т

5 Г

• J dx erf 0 0       L

f 5 - x '- cd ) ç

( 2 40d J

+ erf

f x ' + cS ) ç

( 2 40S ^J

• exp

( ^x '^{- x - u} , ^t ) ² 4 а т

.

Следует отметить, что соотношения (16), (17) представляют собой верхнюю оценку температуры, а формулы (18), (19) - нижнюю оценку. Замена комбинированной ленты на сплошную,

прерывистую или композиционную сводится к использованию других выражений для функций

b ( x , t ) и d ( x , t ) , отличных от (13) и (15).

Численные оценки показывают, что интегралы по переменной x ' в формулах (18), (19) в основном набираются в области 0 <  x ' <  5 . А именно, изменение области интегрирования в

Выражения (16) - (24) дают исчерпывающее общее решение задачи о теплообмене при шлифовании в рамках метода последовательных приближений. Простота и физическая прозрачность этих соотношений делают их достаточно удобными для численных расчетов.

Полученные формулы использованы для теоретического исследования тепловых процессов при ленточном шлифовании сплошными, прерывистыми, композиционными и комбинированными лентами.

формуле (19) уменьшает величину соответствующего интеграла не более чем на 20 %. В то же

время сама поправка к нулевому приближению

не превосходит 15 %, то есть

T ⁽¹⁾ - t ⁽⁰⁾

T (0)

< 0,15.

Если учесть, что подынтегральная функция T ⁽⁰⁾ представляет собой верхнюю оценку температуры поверхности шлифуемой заготовки, то обрезание интеграла в формуле (19) вносит в расчеты суммарную погрешность, не превышающую 5 % (при среднеконтактной температуре в 1000 ^оС - максимум 50 ^оС). То есть в данном приближении погрешность расчетов не превосходит погрешности эксперимента.

Описанное приближение позволяет существенно упростить расчетные формулы. Так при вычислении интеграла (19) в области 0 <  x ' <  5 значительно упрощается выражение для функции граничных условий:

b ⁽ x , t ^{) —} « тС f_x ⁽ t ^{) + а} сож f , ⁽ t ) , ⁽²⁰⁾ где

ВЫВОД

• 1.    Получена схема распределения тепловых потоков при шлифовании комбинированной абразивной лентой.

• 2.    Получено решение задачи по расчету температурного поля в заготовке при шлифовании абразивными лентами различных типов, а именно: со сплошной рабочей поверхностью, прерывистыми, композиционными и комбинированными. Решение реализовано в программе расчета.