Аналитика процессов, протекающих в камере сгорания нетрадиционной тепловой машины (двигателя) в условиях реализации полных нагрузок

В настоящее время в классе ТМ господствующими являются поршневые ТМ (в частности, ДВС с КШМ). Большая распространенность этих машин обусловлена высокой экономичностью их РЦ, надежностью, достаточно высоким сроком службы и отработанной технологией производства. В двигателях такого типа движение поршня, являющееся возвратно-поступательным, посредством КШМ преобразуется во вращательное движение коленчатого вала. При этом среди механизмов и систем двигателя КШМ на сегодняшний день относится к наиболее высокотехнологичным, сложным в конструктивном отношении и дорогостоящим в изготовлении узлов ДВС. Хорошо известны данные о том, что на долю затрат по изготовлению КШМ приходится от 25 до 40 % в себестоимости производства двигателя в целом. Вместе с тем для обеспечения работоспособности КШМ необходимо наличие в конструкции двигателя большого количества трущихся элементов (кинематических пар трения, в частности скольжения). А это обстоятельство, в свою очередь, вызывает увеличение механических потерь, ухудшает механический КПД, снижает массогабаритные параметры двигателя, а зачастую служит препятствием для дальнейшего совершенствования и экономических показателей.

Сказанное означает существование значительного интереса к отысканию новых, оригинальных схемных решений двигателей [1]. Так, например, разработаны – а некоторые из них достаточно широко распространены – такие конструктивные исполнения двигателей, как газотурбинные, роторные и роторно-поршневые [2, 3], свободнопоршневые [4] тепловые машины, а также бескривошипные и бесшатунные [5, 6]. К наиболее известным на сегодня следует отнести двигатели конструкции С.С. Баландина [7, 8] и Ф.Г. Ванкеля [9, 10]. Однако и упомянутым выше тепловым машинам присущи определенные недостатки, к наиболее существенным из которых относятся конструктивная и технологическая сложность, а также дороговизна в изготовлении.

В последние несколько лет учеными и инженерами кафедры ДВС Южно-Уральского государственного университета (ЮУрГУ) был предложен целый ряд технических решений по созданию новых конструктивных схем двигателей, не являющихся традиционными в общепринятом понимании ДВС как тепловой машины, построенной на основе КШМ. Эти (предложенные на кафедре ДВС ЮУрГУ) машины получили название БПМ. По мнению авторов-разработчиков, такие схемы БПМ позволяют в значительной мере исключить недостатки, присущие тепловым двигателям на основе КШМ, и вместе с тем обеспечить объединение достоинств как кривошипно-шатунных ТМ (относительно высокая степень сжатия РТ, отработанная технология производства), так и, например, свободнопоршневых (отсутствие КШМ и в частности деталей, движение которых является сложным, плоскопараллельным – коленвала, деталей шатунной группы) [11].

Основное принципиальное отличие предложенных бесшатунных схем от других известных ТМ определяет то обстоятельство, что в БПМ обеспечивается техническая возможность прямого преобразования движения одного и того же поршня – возвратно-поступательного во вращательное, что предопределяет наличие у таких машин ряда преимуществ перед традиционными, кривошипно-шатунными. К этим преимуществам относятся прежде всего хорошие экономические показатели, полная уравновешенность оппозитных конструкций и схемных решений с противоположно движущимися поршнями, а также значительно более благоприятные удельные показатели – массогабаритные и мощностные. Интересы создания и разработки таких ТМ требуют разработки соответствующих методов решения задачи.

Особенности конструкции и аналитического описания процессов,формирующих РЦ БПМ(Д)

Конструктивные особенности БПМ(Д) применительно к двухтактной схеме реализации РЦ в цилиндре поясняются схемой (рис. 1). Осесимметричный поршень 1 в такой БПМ соединяется с кареткой 3 МПД при помощи штока 2, верх которого (штока) установлен в подшипнике, расположенном внутри поршня на его днище. Низ штока укреплен в каретке неподвижно. Цапфы оси 4, проходящей через сквозное отверстие в каретке, снабжены подшипниками, катящимися при работе БПМ по БД, образуемой криволинейными торцовыми поверхностями цилиндрических вставкок 6, установленных неподвижно в корпусе машины. Выходной вал взаимодействует с кареткой МПД посредством своей верхней части, выполненной в виде двухрожковой вилки с возможностью перемещения каретки в пазу, образуемом рожками вилки выходного вала.

За счет того, что поршень выполнен осесимметричным, а также имеет подшипниковое соединение со штоком каретки МПД, обеспечивается снижение тепловой и механической нагру-женности поршня и, как следствие, его (поршня) тепловых и механических напряжений и деформаций в процессе работы двигателя. При этом выходной вал нагружен только крутящим моментом и не подвергается воздействию других видов механических напряжений. БПМ такого типа отличается и другими преимуществами относительно ТМ других конструктивных схем. К этим преимуществам относится, в частности, и то, что в такой БПМ отсутствуют боковые, или нормальные силы, действующие на детали ЦПГ (поршень и цилиндр) перпендикулярно боковой поверхности поршня, меняющие к тому же свой знак в процессе работы двигателя вследствие перекладки поршня в цилиндре в кривошипно-шатунных двигателях, что приводит в ДВС с КШМ к повышению механических потерь и ударно-вибрационных нагрузок, а также к увеличению износа основных деталей ЦПГ.

Еще одним достоинством поршня осесимметричной формы является гораздо большая технологичность его изготовления, обусловленная отсутствием необходимости в использовании сложных процессов формообразования продольного и поперечного профилей боковой поверхности. При этом также минимизируются массогабаритные параметры такого поршня.

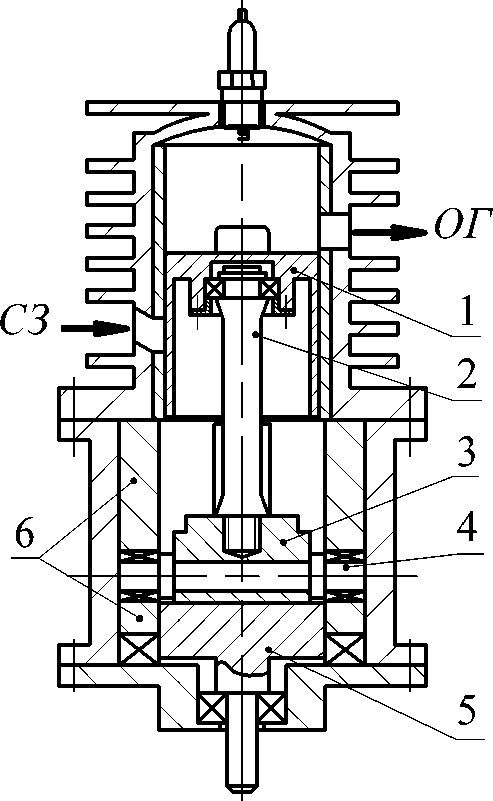
Рис. 1. Конструктивная схема двухтактной БПМ – двигателя с невращающимся поршнем и вращающимся выходным валом:

1 – поршень; 2 – шток; 3 – каретка МПД; 4 – ось каретки МПД;

5 – выходной вал; 6 – БД

На состояние РТ такой ТМ, определяемое рядом параметров (в частности, давлением, температурой, удельным объемом) и обусловливающее получение определенных технико-экономических параметров БПМ – двигателя, оказывает влияние целый ряд факторов, к основным из которых относятся характеристики тепломассообмена, закономерности процессов сгорания ТВС, кинематические параметры конструктивной схемы (в частности, закономерности перемещения поршня), характер нагрузки, режим работы двигателя. Оценка численных значений этих параметров, как и характера их изменения в течение РЦ, относится к одной из важных задач на стадии проектирования, исследования и доводки ТМ. Применительно к условиям проектирования такого рода расчёты (расчётные исследования) лежат в основе определения основных размеров тепловой машины. В частности (для поршневого ДВС), диаметра цилиндра и хода поршня, а затем – и выявления характера изменения показателей машины при её работе на различных режимах. Например, на режимах полных, но и частичных нагрузок также.

Для уже созданных ТМ такая оценка имеет значение с точки зрения сопоставительного анализа их (машин) применительно к различным условиям использования, а также – сопоставительной оценки достоинств и недостатков конкретных схем, типов и образцов ТМ.

Важны особенности протекания РЦ бескривошипной тепловой машины, конструктивная схема которой приведена на рис. 1, в сходственных условиях использования с традиционной двухтактной кривошипно-шатунной ТМ (двигателем) при одинаковых значениях их основных конструктивных параметров (диаметр цилиндра, ход поршня).

Решение этой задачи опирается на использование соответствующих методов прогнозирования (моделирования, аналитического описания) процессов и численную оценку параметров, характеризующих обстоятельства (условия) работы ТМ.

Решающими при определении показателей и параметров РЦ (применительно к двухтактным поршневым ДВС) являются процессы сжатия, сгорания, расширения и сопровождающие их явления теплообмена со стенками КС, цилиндра, а также особенности смесеобразования. Опыт оценки влияния названных обстоятельств на параметры РЦ ТМ в этой работе учтен. В частности, параметры процессов сжатия и расширения рассматриваются как параметры политропических процессов. В них численные значения p, v, T определяются начальным состоянием РТ в исходной точке процесса, условиями теплообмена со стенками, а также кинематикой движения поршня. Особенности перемещения поршня (его кинематика) в случае использования двухпериодной беговой дорожки могут, применительно к любому текущему моменту РЦ, быть отображены соотношением ст(а) = 1 — cos2a. Функция особенна тем, что она безразмерная. Характером ее протекания определяется текущее положение поршня. Функция универсальна. В том смысле, что ее численные значения не зависят от конкретного поршня, двигателя в целом. Из анализа этой функции вытекает ряд важных аналитических соотношений. Например, кинематические функции объема РТ: у (а) = 1 + ^1 ■ ст (а); v = vc ■ у (а) = — ■ у (а). Названные обстоятельства используются для описания процессов РЦ БПМ(Д).

Известно достаточно большое количество уравнений, описывающих процесс выделения теплоты в двигателях [12, 13]. К получившим широкое распространение при моделировании процессов в двигателях относится уравнение, предложенное профессором И.И. Вибе [14, 15]. Оно является универсальным: им хорошо отображаются процессы выделения теплоты при горении смесей на основе углеводородных топлив (дизельные, бензовоздушные, керосиновые смеси и др.).

В исследовании И.И. Вибе [16, 17] процесс выделения теплоты в КС двигателя подчиняется относительно простому соотношению:

x = 1 - exp

/   \ m + 1

I

- 6,908 - I

I 4)

, или x = 1 - exp

- 6,908

m + 1

I -1 l Ф-.)

где t , φ – текущее время (текущий угол ПКВ), отсчитываемое от момента начала сгорания; t z , φ z – продолжительность сгорания, соответственно в с и град. ПКВ; m – показатель характера сгорания.

Предварительным сжатием РТ обеспечивается подготовка горючей смеси к сгоранию. В ДВС, работающих на лёгком топливе (в частности, на бензинах), момент начала сгорания можно отнести к управляемым процессам: это обеспечивается посредством управления подачей напряжения на электроды свечи зажигания. Названное условие оговаривается, как правило, на стадии проектирования ДВС. Межэлектродный электрический разряд служит началом новой фазы РЦ – фазы сгорания. Динамика сгорания определяется качеством горючей смеси, характеризуемым видом применяемого топлива и численным значением α с , а также параметрами состояния РТ в момент разряда на электродах свечи зажигания р y , Т y , v y .

Качество процесса горения во многом определяется значением коэффициента эффективности сгорания f = ^ • 5. Параметр 6 (коэффициент выделения теплоты) характеризует полноту выделения теплоты и во многом определяется значением α с и качеством процесса смесеобразования. Для случаев, когда α с больше единицы (для окисления компонентов топлива в полной мере достаточно окислителя), численное значение δ принимается равным 1. Когда окислителя (воздуха) недостаточно, α < 1, можно полагать, что часть углерода топлива сгорает в окись углерода, и обусловленные этим потери теплотворной способности топлива оцениваются с использованием соотношения [18]:

ДНи = 4,13(1 — а)Ь0/, МДж / кг топлива, в котором L0/ определяется элементарным химическим составом топлива.

На основании записанного для Δ H u получаем:

, ни— ДНи

• ⁶ Н

Потери теплоты в стенки оцениваются параметром ψ . И в этой связи он получил название коэффициента использования теплоты. Методы оценки ψ опираются на моделирование теплообменных процессов и в этой связи – на ряд эмпирических коэффициентов, характеризующих конструктивные особенности КС, условия смесеобразования, движение смеси и др. По этой причине, особенно при создании и исследовании новых машин, при назначении численного ψ опираются на статистический опыт.

Авторы для оценки численных значений ψ использовали эмпирическое соотношение, полученное на основании обработки статистического материала (в том числе литературного) по бензиновым ДВС с внешним смесеобразованием. Можно полагать, что

У = 0,8 + 0,1-Ne + 0,08 • n, где Ne =

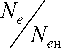
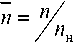
Еще раз отметим, что, так как расчёты выполнялись применительно к

режимам работы двигателей на «полной» нагрузке, N_e и п принимались равными единице.

Аналитическое описание процессов, формирующих РЦ двухтактной БПМ(Д)

На основании сказанного совокупность процессов, протекающих в КС двухтактной поршне- вой ТМ (двигателя) в период осуществления РЦ, может быть отображена системой:

•

Р = P a •

T = T a •

У (аа)

У ( ^а )

У (аа )

• ^ст 1 +

1 n , ^{- 1}

_ У ( а ) _

x = 1 - exp

qz

² q z ⁽ x j ^- x j - 1 ) + P j - 1 ( K j - ( j - 1 ) • v j - 1 ^- v j )

K - ( - 1 ) • v - 1

-

v

• ^ст 2 + P z ^-

у ( ^а )

n ₂

У ^{( а} ь ) .

• ст 3

• ^СТ 1 ⁺

T y

•

P j" v j

P y • v y     ^e j

• ^СТ 2 ⁺ T z •

У (а)

n ₂

- 1

_ У ( ^а ь ) _

• ^ст 3 ;

z x m +1

- 6,908 1 - ^ I

I y z J

5 • H u

( 1 + ^a c • L 0/ ) ( 1 + y ) ;

K = — ; k - 1

k = 1,259

-

76,7 T

-

;

0,0372 )

0, 005-- I • X ;

^a c J

У ( а ) = 1 + ^£ 2 1 • ст ( а ) ;

va - £ -1    ( x v=7 1+—'ст(а) '

Индексы при параметрах обозначают их (параметров) принадлежность к характерным ( a , y , z ) моментам РЦ (рис. 2), текущим (при сгорании – j ) точкам процессов, а также указывают на то обстоятельство, что численное значение параметра является средним для рассматриваемого уча-

Kj+Kj-1\ стка (например, Kj_(j_1) = -^-у—).

Для сокращения записей в системе уравнений использованы функции Хевисайда [20]. Их численные значения определяются условиями:

^СТ 1 =

1; 90 <  а <  ау ;	".	90 <  а <  ау ;	-1	90 <  а <  ау
0; ау <  а <  а2 ; ст 2 = •	1;	ау <  а <  а2 ; ст 3 = •	0;	а < а < а yz
0; а2 <  а <  270 .	. 0;	аг <  а <  270 .	. 1;	а2 <  а <  270

;

;

.

Единственность решения системы определяется численными значениями начальных и граничных условий. К таким условиям относятся прежде всего значения параметов состояния РТ в момент, соответствующий α = αа = 90 град. ПГВ (для БПМ). Для двухтактного ДВС с КШМ αa = 180 град. ПКВ. Для этого момента p = pа; T = Tа; v = vа ; ψ(α) = ψ(αa); σ(α) = σ(αa). К гранич- ным условиям могут быть отнесены значения αс, ε, δ, Ѕ/D, а также кинематическая функция перемещения поршня. Ее численные значения определяют динамику движения элементов МПД и уровень их механического нагружения. На стадии первоначального проектирования БПМ(Д) целесообразно использование двухпериодной беговой дорожки [19]. В этом случае профиль функции опишется соотношением:

SS s = — (1 - cos 2a) = — ■ 2sin2 a = Sn sin2 a ,

2                2п в котором Ѕп – полное перемещение поршня.

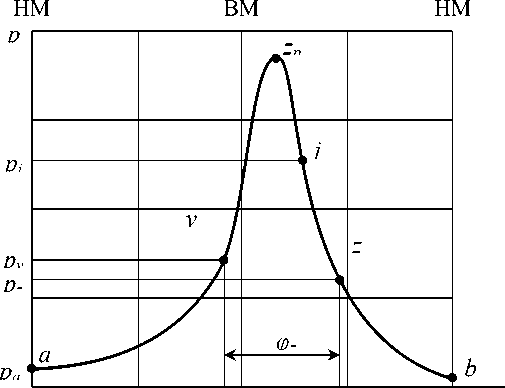
90                α 180       α z        270 α град.

Рис. 2. Схема протекания процессов РЦ (применительно к БПМ(Д), работающей по двухтактному циклу)

Распространение решения системы на весь период реализации цикла позволяет определить численные значения основных показателей РЦ. В частности, l u , p u , η i , g i ; l u – удельная индикаторная работа цикла; p u – среднее индикаторное давление цикла; η i – индикаторный КПД; g i – удельный индикаторный расход топлива.

7    7        1       1         1                     \ nbpjj ^{+ P}j + 1 /           \      1

lu = la - y + ly - z + к - b =----J Pava - Pyvy ) + L----( vj+1 + vj ) +----?( PV - Pbvb ) ;

П 1 — 1                      1 2                     П 2 — 1

pu

к = lu (1 -Уп ) . vh vc (e - 1) ’

n i =

lu (1 - Уп )(ac ■ L0 + 1) ,

H u ■ ^

;

gi =

n i- H u

В записанных выражениях коэффициентом ψ п учитывается потерянная в период процессов смены РТ доля хода поршня.

Сопоставительная оценка параметров, характеризующих работу БПМ(Д)и двигателя с КШМ в сходственных условиях нагружения

На базе рассмотренного расчётного инструментария с использованием упоминавшихся соотношений определим характер изменения текущих параметров РЦ (прежде всего p , T ) бескриво-шипной тепловой машины применительно к условиям работы с полной нагрузкой. Основными исходными данными приняты: p 0 = 0,101, МПа; T 0 = 293; ε = 7,5; α с = 0,87; m = 3,5; φ z = 23,8 град. ПГВ.; θ = 12,68 град. ПГВ.; δ = 0,82; ψ = 0,9; Δ T = 30; S п = 58 мм.

Результаты расчёта (в данном случае – применительно к текущим давлениям и температурам РТ) в функции α применительно к одному обороту грузового вала приведены на рис. 3.

Для кривошипно-шатунного двигателя той же размерности (диаметра цилиндра, хода поршня, степени сжатия) и аналогичных условий по нагрузке характер протекания параметров цикла ( p , T , x , w ) в течение одного оборота КВ иллюстрируется рис. 4.

Повторим, что рис. 3, 4 иллюстрируется характер изменения параметров РЦ при работе тепловых машин в сходственных условиях нагружения (одинаковые α с , ε , S п , m , φ z ) в течение одного оборота грузового (БПМ) и коленчатого (ТМ с КШМ) валов. Различие в том, что при двухпериодной беговой дорожке (БПМ) за один оборот ГВ совершается два РЦ, а в двигателе с КШМ – один. И, так как временная продолжительность циклов одинакова (при разнящихся в 2 раза n ), производство механической энергии БПМ(Д) за один оборот в два раза превышает соответствующее ей производство энергии двигателей с КШМ [19].

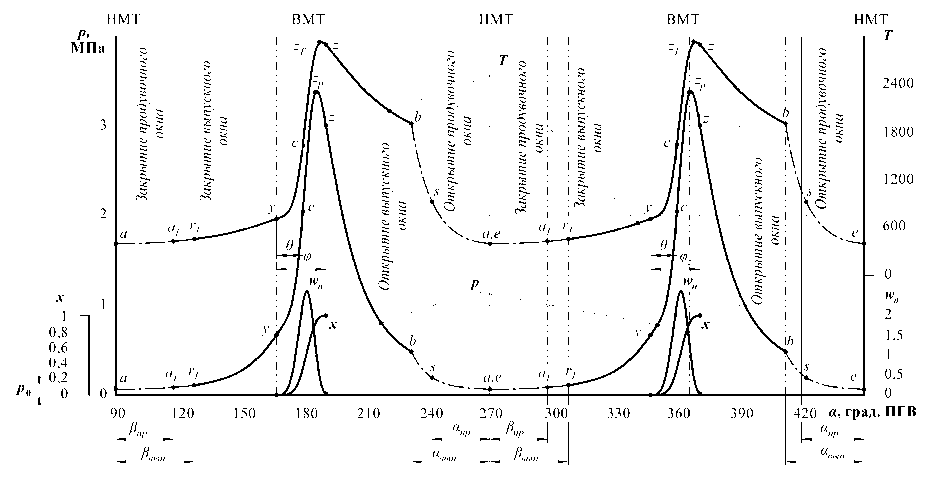
Рис. 3. Изменение давлений, температур, доли сгоревшего топлива и скорости выгорания топлива в течение одного оборота ГВ при работе на режиме полной нагрузки ( ε = 7,5; α с = 0,87; S п = 58 мм; t z = 17,65·10^–4 с)

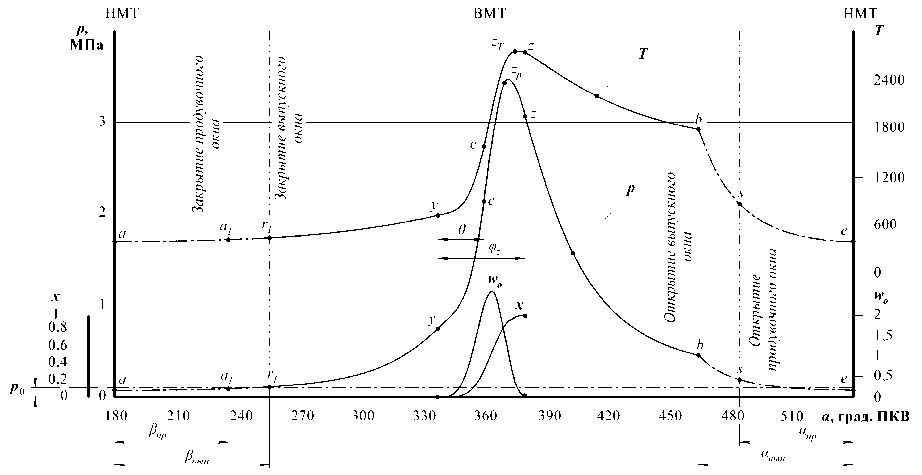
Рис. 4. Изменение параметров РТ в течение одного оборота КВ при работе кривошипно-шатунного двигателя с полной нагрузкой (ε = 7,5; αс = 0,87; Sп = 58 мм; tz = 15,74·10–4 с)

Сопоставительная оценка таких параметров, как p макс , p y , T макс , T y , p z , T z и др. (см. рис. 3, 4, 5), позволяет сделать заключение о том, что численные значения их применительно к двигателям рассматриваемых типов, работающих с одинаковой нагрузкой (при разнящихся в два раза n ), фактически совпадают.

Детализированный анализ характера изменения индикаторных показателей тепловых машин возможен с использованием ( p–t )-диаграмм. На рис. 5 такое сопоставление параметров, иллюстрируемых рис. 3 и 4 в координатах, когда независимой переменной рассматривается относительное t / t ц время (продолжительность отрезка времени выбрана равной продолжительности цикла, за начало отсчёта принята точка а индикаторной диаграммы), приведено.

нмт                              вмт                              нмт

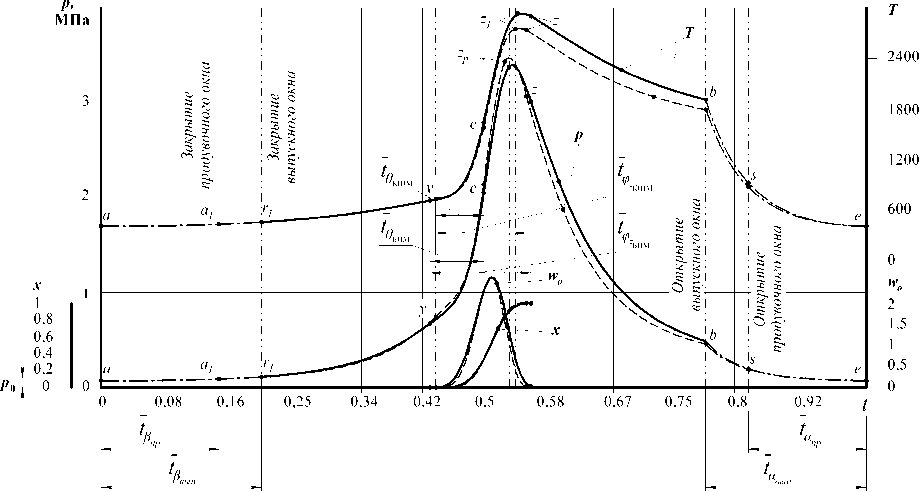
Рис. 5. Изменение параметров РТ в функции относительного времени цикла в условиях работы двигателей (БПМ и двигателя с КШМ) с одинаковой нагрузкой ( ε = 7,5; α с = 0,87; S п = 58 мм); – БПМ;         – двигатель с КШМ

Анализ характера изменения параметров РТ в течение цикла (см. рис. 5) применительно к одинаковым условиям нагружения машин позволяет заключить: при одинаковых нагрузках рабочие циклы ТМ (БПМ с двухпериодной беговой дорожкой и двухтактного двигателя с КШМ) идентичны. Практически одинаковы экстремальные значения показателей ( p макс , T макс ), близки по значениям и первые производные от p и T по времени. Одинаковы и мощности циклов.

Таким образом, сопоставительный анализ особенностей протекания РЦ тепловой машины нетрадиционной схемы и ТМ на базе кривошипно-шатунного механизма даёт основания заключить, что динамика протекания параметров этих машин (в сходственных условиях нагружения) практически одинакова.

Заключение

Применительно к схеме поршневой машины-двигателя с преобразованием возвратнопоступательного движения поршня во вращательное грузового вала предложена методика расчёта текущих параметров рабочего тела в цилиндре и показателей цикла. Результаты расчётных исследований показателей цикла бескривошипного ДВС с двухпериодным механизмом преобразования движения поршня сопоставимы с показателями кривошипно-шатунного двигателя в аналогичных условиях нагружения. При этом мощность БПМ(Д), развиваемая в период одного оборота, в два раза превышает относящуюся к одному обороту мощность двигателя с КШМ.

Анализ показателей РЦ бескривошипной поршневой тепловой машины и машины-двигателя с КШМ применительно к одинаковым условиям реализации РЦ (по величине ε , α с , m , t z , t θ , S п ) да-

ёт основания утверждать, что бескривошипный двигатель по таким параметрам цикла, как p макс , T макс , p и , η i , не уступает поршневому двигателю с КШМ. При этом производимая им работа, приходящаяся на один оборот грузового вала, превышает (в два раза) работу, производимую соответствующим двигателем с КШМ. Названное обстоятельство даёт основания утверждать, что комплексный показатель степени совершенства и коммерческой доступности (МГЦЭ – мощность, габариты, цена, экономичность) бескривошипных машин окажется по численному значению более благоприятным, чем у машин с КШМ.