Анализ адаптационной комфортности различных конструкций эндопротезов тазобедренного сустава

При проектировании ножки эндопротеза тазобедренного сустава прогнозируется её прочность, упругость, биосовместимость материала и его способность к биофиксации в кости за счет прорастания трабекул костной ткани в поры напыленного покрытия. Однако, как показывают исследования последних лет [1], в 69,7% случаев долговечность использования протеза определяется временем развития расшатывания ножки имплантата в кости, вызванной снижением упругих и прочностных характеристик кости из-за увеличения пористости костной ткани вокруг ножки имплантата. Поскольку развитие пористости является адаптационным откликом костной ткани на изменение нагрузки, передаваемой на кость имплантатом, представляется необходимым при проектировании протеза учитывать влияние формы ножки на развитие пористости кости и выбирать значения параметров формы, обеспечивающие эргономичные (комфортные для кости) свойства протеза.

В настоящей работе влияние формы ножки эндопротеза на развитие пористости кости исследуется с помощью последовательного применения двух моделей: пространственного линейно упругого напряженно-деформированного состояния системы бедренная кость–имплантат и адаптационных изменений пористости и модуля упругости костной ткани вокруг ножки имплантата. Анализ полученных результатов моделирования позволил сформулировать критерий оценки влияния формы ножки имплантата на скорость роста пористости кости (критерий адаптационной комфортности конструкции ножки эндопротеза). Для вычисления критерия не требуется трудоемкого решения соответствующей эволюционной задачи об адаптационных изменениях в кости, достаточно найти отклонение поля деформаций в протезированной кости от гомеостатического или некоторого эталонного поля деформаций. Применение критерия продемонстрировано при оценке формы трех наиболее распространенных типов конструкций эндопротезов.

Модель системы кость–имплантат

Согласно описанным в литературе экспериментальным данным система бедро– эндопротез представляет собой неоднородное анизотропное линейно упругое тело сложной геометрической формы (рис. 1). Неоднородность вызвана различием механических свойств эндопротеза, кортикальной и губчатой костных тканей. Эндопротез и губчатая кость являются изотропными, а кортикальная кость – трансверасльно-изотропным материалом.

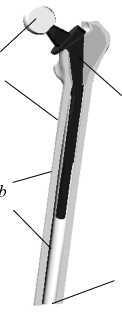
На границе S_t исследуемой области (рис. 1) задана равномерно распределенная нагрузка t со стороны вертлужной впадины таза и мышц. На поверхности расчленения бедра S_u перемещения точек равны нулю, а на границе контакта эндопротеза с костью перемещения непрерывны (предполагается биофиксация имплантата). Напряженно-деформированное состояние бедренной кости непосредственно перед установкой эндопротеза принималось естественным, то есть нулевым. При установке эндопротеза предполагалось, что форма канала в бедре точно повторяет форму поверхности сопряжения ножки и, следовательно, остаточные напряжения и деформации в кости после операции отсутствуют. Данные о силах, действующих на бедренную кость при физиологических нагрузках, рассчитываются с помощью предложенной в работе [2] квазистатической модели ходьбы. Поскольку изменения микроструктуры кортикальной

S u

Рис. 1. Расчетная модель системы кость-имплантат. S b - полная поверхность кости, включая поверхность мозгового канала,    S p  - поверхность имплантата,

S b n S p - поверхность контакта кости с имплантатом, S t - поверхности нагружения, S u - поверхность поперечного расчленения бедра

а

б

Тип I

Тип II

Тип III

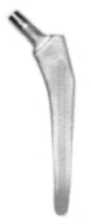
Рис. 2. Внешний вид (а) и компьютерные представления (б) исследуемых типов конструкций эндопротезов тазобедренного сустава костной ткани происходят в течение длительного промежутка времени, при определении напряженно-деформированного состояния системы кость-имплантат используются средние за цикл шага значения сил, действующих на бедренную кость.

Механическое поведение данной конструкции описывается системой уравнений линейной теории упругости

V- о = 0, V x е V ,

£ = -(Vu + (Vu)T ),  Vx е V , a = E(x): £, Vx e V ,(3)

u = 0, Vx e Su,(4)

n• a = 0, Vx e Sb\((Sp nSb)uSu .S),(5)

n • a -1 = 0, Vx e St.(6)

В системе кость–имплантат исследуются три типа имплантатов с различным поперечным сечением ножек: овальным (тип I), круглым (тип II), прямоугольным (тип III). На рис. 2 изображен внешний вид выбранных конструкций эндопротезов и их компьютерные представления.

Использование данных томографического исследования нижней конечности человека [3] позволило воспроизвести индивидуальную геометрию бедренной кости. На рис. 3 изображен внешний вид построенных моделей системы бедро–имплантат.

На рис. 4 представлено распределение продольных деформаций на медиальной и латеральной сторонах бедренной кости при установке различных моделей эндопротезов, полученное решением задачи (1)-(6) методом конечных элементов.

Приведенные данные показывают, что при установке имплантатов различного типа в кости наблюдаются продольные деформации сжатия различного уровня как на медиальном, так и на латеральном крае кости. Однако во всех трех системах кость– имплантат более сжатым является медиальный край, что соответствует правильному направлению изгиба бедра и подтверждает адекватность компьютерной модели исследуемой системе кость–имплантат. Различие в уровнях продольных деформаций, очевидно, отражает влияние формы поперечного сечения ножки используемого имплантата и предполагает различную стимуляцию адаптационного процесса в кости бедра при эксплуатации протеза.

Модель адаптационных изменений кости

Система уравнений, описывающая адаптационные изменения структурных, механических и геометрических параметров кортикального слоя бедренной кости, имеет вид [4, 5]:

• •    уравнение изменения радиуса гаверсова канала r hav :

  r >  r >  r . max hav min ,

  r <  r . r >  r .

  hav min ,         hav max ,

  
  
  
  

drhav __< ^{C ( £} 11   ^£ hom ),

"dt" "I 0, где rmax,, rmin – максимальное и минимальное значения радиуса центрального канала остеона, соответственно, shom - равновесное значение продольных деформаций; С -коэффициент адаптационной чувствительности:

C = ( X b + K bc X c ) a b

£  -£ max min где Xb, Xc - части эндостальной поверхности, занимаемые остеобластами и остеокластами, соответственно (Xb = 0,94, Xc = 0,06 [6]), Kbc - отношение скорости резорбции ac остеокластами к скорости производства ab остеобластами костного

Тип I

Тип II

Тип III

Рис. 3. Пространственная модель системы бедро–имплантат

а

_2 ОООе-ООЗ ll .667е-003

ЗЗЗе-ООЗ

1 ОООе-ООЗ

6.667е-004

б

I

II

III

III

З.ЗЗЗе-004

5.821е-011

-З.ЗЗЗе-004

-6.667е-004

-1 ОООе-ООЗ

1 1 .ЗЗЗе-ООЗ

1.667е-003

2 ОООе-ООЗ

—2 .ОООе-ООЗ Я,667е-003 .ЗЗЗе-ООЗ

.1 .ОООе-ООЗ

6.667е-004

З.ЗЗЗе-004

15.821 е-О11 |-З.ЗЗЗе-004

-6.667е-004

1 .ОООе-ООЗ

1 .ЗЗЗе-ООЗ

1 667е-003

2 ОООе-ООЗ

Рис. 4. Распределение продольных деформаций на медиальном (а) и латеральном (б) краях бедренной кости при осредненной за цикл шага нагрузке вещества (ac =0,89+1,74 мкм/день, ab =0,06+ 0,49 мкм/день [7]), emin, emax - принятые в модели нижняя и верхняя границы интервала деформаций, в котором изменяется скорость перестройки при изменении нагрузки (emin = - 0,011, emax = 0,015 [5]);

• •    уравнение изменения модуля упругости костной ткани E 11 в направлении оси X 1 :

  dE 11 dt

  
  

  - E ost CS v (e_n -e h _O m ),

  
  
  
  

  гаверсов канал

  

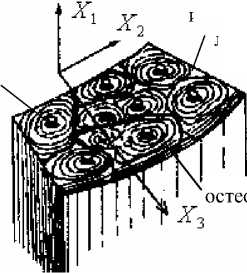
  Рис. 5. Структура кортикального слоя диафиза бедренной кости

  
  

  интерстициальные ламеллы

  
  

  б

  а

  

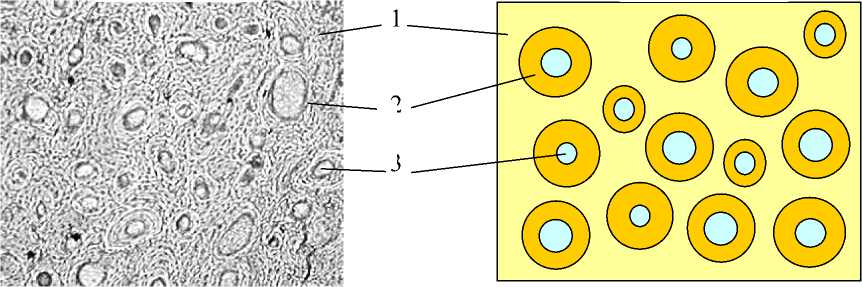
  Рис. 6. Увеличенная фотография структуры (а) и принятая модель структуры (б) кортикального слоя бедра. 1 – интерстициальные ламеллы, 2 – остеон, 3 – гаверсов канал

  
  

  где E ost — модуль упругости материала остеона ( E _ost =1872 кгс/мм² [8]), S V — удельная (на единицу объема костной ткани) площадь внутренней поверхности гаверсовых каналов;

уравнение изменения пористости р :

d p = C V ( 8 11 dt

—

^£ hom ) ;

• •    уравнения изменения внешнего ( R ext ) и внутреннего ( R int ) радиусов диафиза бедренной кости:

^ = C ( 8 11 — 8 _h„ ), dt

dR ext

^{( 8} 11    ⁸ hom ) ^.

dt

Если нагрузка на бедро равна среднему за день типичному (гомеостатическому) значению, то поле продольных деформаций 8 11 ( x ) в формулах (7), (9) — (12) равно гомеостатическому и адаптационных изменений в кости не происходит. При отклонении нагрузки на бедро изменяется поле продольных деформаций и скорость изменения соответствующей величины в формулах (7), (9) — (12) становится отличной от нуля, следовательно, начинается процесс перестройки.

а

б

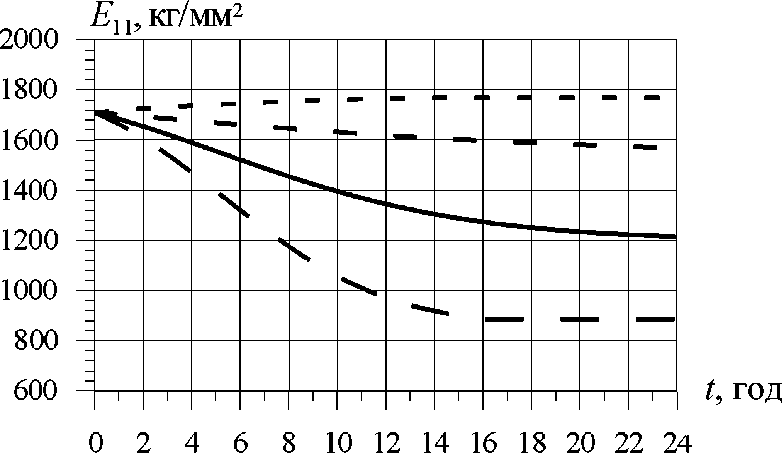
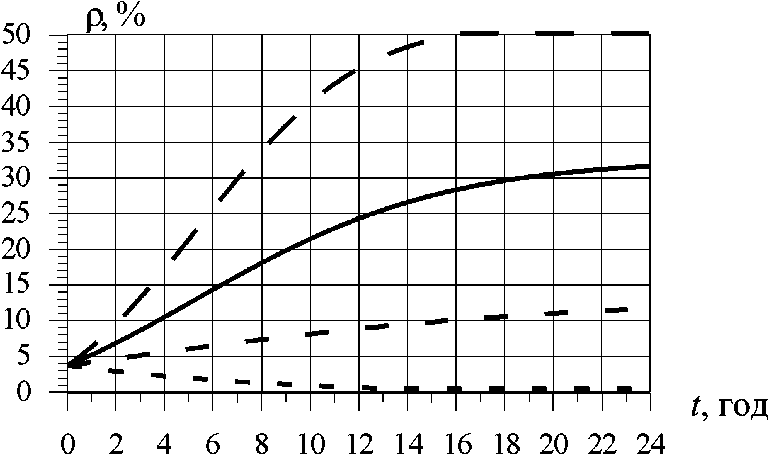
Рис. 7. Адаптационное изменение пористости (а) и модуля упругости (б) при различном уровне изменения внешней нагрузки

Изменение нагрузки

• -    -  +10%

• ■    -   -10%

  ----- - 30%

• -    — - 50%

Процесс адаптационных изменений во времени пористости и модуля упругости кортикальной костной ткани исследован для участка диафиза бедра, охватывающего ножку эндопротеза. Остеонная структура костной ткани участка и главные оси материальной симметрии представлены в виде схемы на рис. 5.

Для компьютерного моделирования адаптационного поведения кортикальной костной ткани использовалась структурная модель кости, изображенная на рис. 6. Кортикальный слой бедренной кости моделируется линейно упругим, анизотропным двухфазным композиционным материалом. Предполагается, что матрица (интерстициальные ламеллы) армирована полыми цилиндрическими включениями (остеон с центральным каналом). Продольная ось остеона совпадает с осью изотропии костной ткани X 1 . Центральный канал остеона рассматривается как цилиндрическая полость. Наличие каналов Фолькмана не учитывается.

Процесс адаптационных изменений пористости и модуля упругости костной ткани исследован на компьютерных моделях цилиндрических образцов с площадью поперечного сечения 1 мм2, вырезанных из участка диафиза бедра, охватывающего ножку эндопротеза и ориентированного вдоль оси остеона. Согласно предложенной модели картина адаптационных изменений пористости и продольного модуля упругости образцов при различных уровнях изменения внешней нагрузки имеет вид, представленный на рис. 7.

Полученные кривые адаптационных изменений показывают возрастание модуля упругости (рис. 7б) и уменьшение пористости (рис, 7а) при увеличении нагрузки на кость, что обусловлено продуцированием костного вещества остеобластами. При уменьшении сжимающей нагрузки на кость имеет место противоположный эффект -уменьшается модуль упругости и растет пористость, что обусловлено активностью остеокластов, резорбирующих костное вещество. Скорость резорбции возрастает с увеличением недогрузки кости, поскольку увеличивается величина деформационного стимула адаптации. Полученное решение соответствует наблюдениям [9, 10] о влиянии снижения и увеличения нагрузки на величину костного баланса в цикле ремоделирования.

Важно отметить, что изменения как пористости, так и модуля упругости имеют монотонный характер. Причем время установления кривых, определяется, в основном, скоростью их изменения в начальный момент времени адаптационного процесса. Этот факт позволил сформулировать критерий адаптационной комфортности конструкции ножки эндопротеза, позволяющий дать сравнительную оценку скорости развития пористости кортикального слоя бедренной кости, вызванного перераспределением физиологической нагрузки на костную ткань после установки имплантата с той или иной формой поперечного сечения его ножки.

Критерий адаптационной комфортности

Математическая формулировка критерия имеет вид:

K ( p ) =

miⁿ⁽— J C ( E 11 ⁽ x , P ) - ^ ref ^{( x )) dV} ), ^{p V} cb V cb

8_n^{( x} , p ) >8 ref ^{( x )},

0,                    ^(X, P) ^ref(x), где p – вектор механических параметров конструкции эндопротеза, Vcb – область кортикальной костной ткани бедренной кости, sref - "эталонное" значение продольных деформаций, С = 0,47 мкм (день-%8). Заметим, что в формуле (13) используются абсолютные значения деформаций.

Согласно предложенному критерию оптимальной является конструкция эндопротеза, обеспечивающая минимальную среднюю по объему кортикального слоя скорость потери костной ткани. Критерий не учитывает возможное упрочнение костной ткани в случае локального увеличения продольной деформации сжатия, так как считается, что упрочнение кортикального слоя бедренной кости не влияет на увеличение риска потери стабильности фиксации эндопротеза в костном ложе. Величина критерия позволяет провести сравнительный анализ различных конструкций эндопротезов с точки зрения оценки степени негативного влияния конструкции имплантата на пористость и упругость кортикального слоя бедренной кости. Чем больше величина критерия, тем быстрее происходит расшатывание ножки данного типа протеза.

Анализ адаптационной комфортности имплантатов

Предложенный выше критерий адаптационной комфортности эндопротеза использовался для анализа трех различных конструкций имплантатов. В качестве "эталонной" конструкции эндопротеза была принята модель первого типа, то есть поле продольных деформаций в бедре после установки имплантата данного типа считалось эталонным s _re f . Очевидно, что для эталонного имплантата величина критерия равна нулю. По рассчитанным полям продольных деформаций в бедре вычислялись значения критерия адаптационной комфортности для конструкций имплатата II и III типов:

K _II = 2,25 ⋅ 10 ^{- 7} , K _III = 0,71 ⋅ 10 ^{- 7} . Согласно полученным значениям критерия использование модели эндопротеза третьего типа даст схожие с моделью первого типа адаптационные изменения параметров кортикальной кости, тогда как при установке конструкции эндопротеза второго типа будет наблюдаться значительно более интенсивное увеличение пористости и уменьшение модуля упругости кости. Более интенсивное увеличение пористости костной ткани при использовании модели второго типа вызвано массивной ножкой эндопротеза, которая "экранирует" нагрузку, необходимую для поддержания неизменности структуры кортикального слоя бедренной кости.

Заключение

Представленная выше двухэтапная методика исследования влияния формы и размеров ножки эндопротеза тазобедренного сустава на развитие пористости кости при эксплуатации протеза позволяет на первом этапе определить распределение продольных деформаций сжатия вдоль оси трансверсальной изотропии остеонной структуры кости, а на втором - дать сравнительную оценку развития пористости при установке протезов с различной формой поперечного сечения ножки. Предложенный критерий характеризует только процесс адаптационной резорбции, поскольку упрочнение костной ткани в случае локального увеличения продольной деформации сжатия не влияет на увеличение риска потери стабильности фиксации эндопротеза в костном ложе. Для вычисления критерия не требуется трудоемкого решения соответствующей эволюционной задачи об адаптационных изменениях в кости, достаточно найти отклонение поля продольных деформаций в протезированной кости от гомеостатического или некоторого эталонного. Поэтому он обладает достаточно высокой вычислительной эффективностью и, следовательно, может быть использован при оптимизации формы ножки эндопротеза. Согласно предложенному критерию оптимальной является конструкция эндопротеза, обеспечивающая минимальную среднюю по объему кортикального слоя скорость потери костной ткани.