Анализ алгоритмов обнаружения импульсного шума на изображениях

Введение. Изображения часто искажаются шумами, появляющимися на этапах их получения и (или) передачи. Причинами возникновения шумов на изображениях могут быть сбои в работе канала связи, шум видеодатчика и др. Одним из основных видов шумов является импульсный шум [1].

Пусть X ij — интенсивность пикселя ( i , j ) исходного изображения X , [ n min , n max ] — динамический диапазон изображения X , Y ,j — интенсивность пикселя ( i , j ) зашумленного изображения Y . Тогда импульсный шум определяется по формуле

Y j = ( X ^ij , ¹ " p (1)

Ri,j, p, где p — вероятность импульсного шума; Rij — заменитель значения интенсивности пикселя (i,j). При Ri,j Е [nmin, nmax] изображение искажается импульсным шумом случайного значения (RVIN), при Ri,j Е {nmin, nmax} — импульсным шумом фиксированного значения или шумом “соли и перца” (SPN).

Различие шумов между SPN и RVIN показано на рис. 1. В случае SPN значение R ij в формуле (1) равно n min (0) или n max (255). Однако в случае RVIN значение R i,j изменяется в пределах от n min до n max .

Одной из основных задач в области обработки изображения является подавление шумов. При этом, как правило, для удаления шумов используются фильтры. Обычно процесс фильтрации включает два этапа: классификацию (обнаружение) и реконструкцию (фильтрование).

В данной работе рассматриваются алгоритмы обнаружения импульсного шума “соли и перца”. Выполнен анализ этих алгоритмов и проведено сравнение результатов, полученных с их помощью.

а

0                    {0,255}                 255

б

0                    {0,255}                 255

Рис. 1. Представление шума “соли и перца” при значении R i,j Е { n min , n max } ( а ) и импульсного шума случайного шума при R i,j Е [ n min , n max ] ( б )

Алгоритмы обнаружения импульсного шума. В [2] предложен алгоритм обнаружения импульсного шума “соли и перца” с использованием адаптивного медианного фильтра (АМФ). Пусть Z — изображение, полученное при применении АМФ к зашумленному изображению Y . Заметим, что в формуле (1) значение Y i,j зашумленного пикселя равно R i,j Е {n _min , n max }, следовательно, множество зашумленных SPN пикселей можно определить следующим образом:

M = { ( i, j ) Е A : Y i,j = Z i,j и Y i,j Е {n min ,n max }} .

Множество неискаженных пикселей определяется как M c = A\M .

В [3] предложен другой алгоритм обнаружения импульсного шума на основе применения параметра β — масштабного параметра, который определяется на основе изменения значений интенсивности в окрестности пикселя. Этот параметр представляет собой разность между значениями интенсивности центрального пикселя Yi,j и соседних пикселей Ym,n в окрестности. Одной из формул, предложенных для масштабной оценки, является формула для среднего значения (Yi,j — Ymn)2 в окрестности вх (i,j) = n

^^^^^^^^^г

J 52 ⁽ Y ij - ^Y mn \ ) , x ( m,n ) ∈ A

где A — множество N — 1 соседних пикселей.

Если значение β -пикселя мало, то он не является искаженным пикселем. В противоположном случае если значение β больше порогового значения, то пиксель является искаженным. В [3] использовалась окрестность размером 3 х 3 ( N = 9). По результатам экспериментов пороговое значение равно 90.

В [4] предложен другой алгоритм обнаружения импульсного шума на основе учета интенсивности и приближения локальной непрерывности. Первое правило сформулировано по значению интенсивности. Пусть t ₁ — порог для обнаружения импульсного шума. Пиксели, значения интенсивности которых меньше значения t ₁ или больше, чем n _max — t ₁ , с большей вероятностью являются искаженными. Множество этих пикселей определяется следующим образом:

N 1 = { ( i,j ) : Y j < 1 1 или Y i j > n max

^^^^^^^^^г

t 1 } •

Второе правило сформулировано на основе применения приближения локальной непрерывности. В соответствии с этим правилом, если характер изменения значений пикселей в локальной окрестности достаточно гладкий, текущий пиксель имеет меньшую вероятность искажения импульсным шумом. Пусть Y i,j — значение интенсивности текущего пикселя,

Рис. 2. Результаты обнаружения импульсного шума с плотностью 20 %: а — зашумленное изображение; б — AdapMed3 х 3; в — AdapMed5 х 5; г — AdapMed7 х 7; д — Threshold123; е — Beta

Y m,n — значение интенсивности восьми соседних пикселей окрестности, t 1 и t 2 — соответственно пороговое значение разности интенсивностей и пороговое значение пропорции, выраженные в процентах. Множество этих пикселей определяется по формуле

N 2 = {( i,j ): count ^{( | У ;}^

^^^^^^^^^г

Y m,n \ > t 2 )       1

------------- / t 3 •

Множество пикселей, искаженных импульсным шумом, является пересечением двух предыдущих множеств:

N = N 1 n N 2 .

В соответствии с экспериментами, проведенными в [4], значения порогов t 1 , t 2 и t 3 равны 0,15; 0,30 и 0,80 соответственно.

Результаты экспериментов. Выполнен анализ и проведено сравнение результатов перечисленных алгоритмов обнаружения импульсного шума “соли и перца”. Оценка результатов определяется по количеству неправильно обнаруженных пикселей и по количеству необнаруженных зашумленных пикселей. Пусть алгоритмы, основанные на АМФ с максимальным размером окрестности 3 х 3, 5 х 5 и 7 х 7, называются AdapMed3 х 3, AdapMed5 х 5 и AdapMed7 х 7 соответственно. Алгоритм, основанный на параметре в , называется Beta. Алгоритм, основанный на порогах t ₁ , t ₂ и t ₃ , называется Threshold123.

Расчеты с использованием указанных алгоритмов проводились для изображения “Лена” с различными плотностями импульсного шума. На рис. 2 представлены результаты обработки изображения “Лена”, искаженного импульсным шумом с плотностью 20 %.

Количество неправильно обнаруженных пикселей (НОП) и необнаруженных пикселей (НП)

Плотность, %	AdapMed3 х 3		AdapMed5 х 5		AdapMed7 х 7		Threshold123		Beta
	НОП	НП	НОП	НП	НОП	НП	НОП	НП	НОП	НП
1	0	7	0	1	0	0	0	9	4	162
2	0	10	0	0	0	0	0	14	3	291
3	0	7	0	0	0	0	0	35	8	425
4	0	9	0	0	0	0	0	62	7	587
5	0	17	0	1	0	0	0	83	15	671
6	0	24	0	0	0	0	0	153	20	838
7	0	25	0	2	0	0	0	188	27	969
8	0	15	0	0	0	0	0	303	48	1139
9	0	33	0	1	0	0	0	353	40	1267
10	0	26	0	2	0	0	0	455	74	1337
15	0	44	0	1	0	0	0	1267	141	2055
20	0	131	0	0	0	0	0	2668	395	2760
25	0	228	0	0	0	0	0	4437	708	3300
30	0	552	0	0	0	0	0	7145	1435	3925
35	0	981	0	8	0	0	0	9737	2182	4345
40	0	1829	0	26	0	0	0	13 171	3246	5061
45	0	2931	0	61	0	0	0	17 111	4560	5709
50	0	4736	0	220	0	1	0	21 173	6310	6256

В таблице указано количество необнаруженных пикселей и количество неправильно обнаруженных пикселей. На рис. 3, 4 представлены результаты сравнения с данными таблицы. Отметим, что алгоритм обнаружения шума, в котором используется адаптивный медианный фильтр с максимальным размером окрестности 7 х 7 (AdapMed7 х 7), дает наилучший результат.

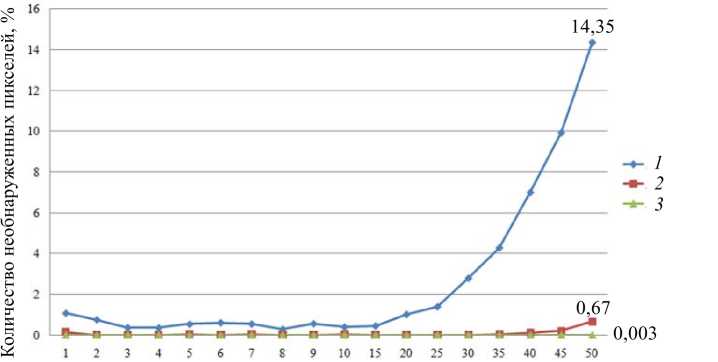
Плотность импульсного шума, %

Рис. 3. Результат сравнения по количеству необнаруженных пикселей алгоритмов AdapMed3 х 3 ( 1 ), AdapMed5 х 5 ( 2 ), AdapMed7 х 7 ( 3 )

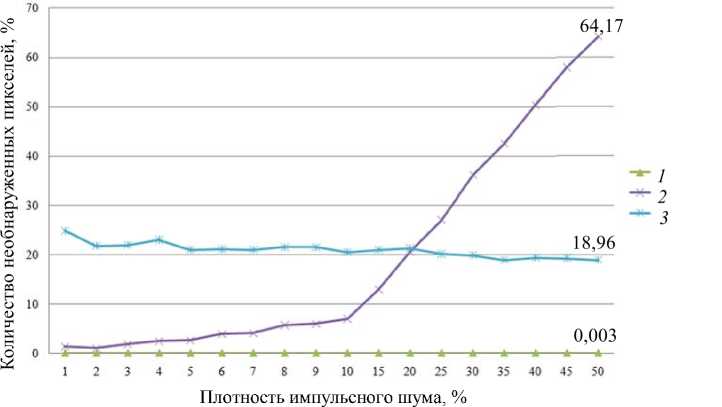
Рис. 4. Результат сравнения по количеству необнаруженных пикселей алгоритмов AdapMed7х 7 (1), Threshold123 (2), Beta (3)

Заключение. В данной работе выполнен анализ и проведено сравнение результатов, полученных с помощью алгоритмов по обнаружению импульсного шума фиксированного значения или шума “соли и перца”. Результаты проведенных экспериментов показали, что алгоритм на основе адаптивного медианного фильтра с максимальным размером окрестности 7 х 7 дает наилучший результат по сравнению со всеми рассмотренными алгоритмами.