Анализ аннигиляции позитрона и электрона и дополнительные возможности позитронно-эмиссионной томографии

Анализ углового распределения вылетающих фотонов при аннигиляции позитрона и электрона имеет важное значение для проектирования позитронно-эмиссионных томографов (ПЭТ). ПЭТ представляет собой самое современное диагностическое устройство, используемое для поиска новообразований на самых ранних стадиях их появления.

К сожалению, механизм процесса аннигиляции электрона и позитрона неизвестен. П. Дираком была предложена модель этого процесса.

Согласно представлениям Дирака [1; 2], аннигиляцию можно представить как переход электрона из состояния с положительной энергией в состояние с отрицательной энергией. Согласно теории вакуумных дырок Дирака, позитрон представляет собой дырку в поле вакуума. Взаимодействие электрона и позитрона, их аннигиляция – это заполнение вакуумной дырки электроном. При этом выделяется энергия в виде двух квантов электромагнитного излучения.

В результате этих расчетов были получены две формулы для дифференциального эффек- тивного сечения рассеяния квантов электромагнитного излучения в телесный угол dQ.

Первая по времени формула была получена

Гайтлером [2]. Эта формула имеет вид:

e 4       [ ( k 0 ) 2 + p 2 + p ² sin² 0

d ^G =----9—iT" 1"——5--

4 (4n)² k ⁰ p I ( k ⁰ ) ² - p ² cos² 0

1                                       (1)

--² p ⁴ sin^{4 0}     2 I d _Q .

^ ( k ⁰ ) 2 - p ² cos² 0^ ’

Формула дана в обозначениях [3], где имеется ее подробный вывод. Использована т. н. рациональная система единиц, в которой скорость света и постоянная Планка равны единице с = Й = 1. В этой системе единиц энергия импульс и масса имеют одну и ту же размерность.

В формуле (1) e – заряд электрона (или позитрона с противоположным знаком), k ⁰ – энергия фотона, p — импульс электрона, 0 — угол между импульсами электрона и одного из излученных фотонов. Формула (1) получена при условии суммирования по всем направлениям поляризации фотонов.

При выводе (1) использована система отсчета, связанная с центром масс взаимодействующих электрона и позитрона, в которой импуль- © Волобуев А.Н., Антипова Т.А., 2014

сы электрона и позитрона равны по модулю между собой и противоположны по направлению P i = - Р 2 = p . Импульсы фотонов также равны по модулю между собой и противоположны по направлению k i = - k 2 [2; 3]. Отметим, что в этой системе отсчета условия наблюдения обоих фотонов одинаковы.

Вторая формула была предложена несколько позже Фейнманом [4] представляет собой ча- стотное или энергетическое распределение вы- летающих квантов:

d ст =

4 2

e to_i

х

64^ 2 4 m ² |p ₊| ( E ₊ + m )

to

сивности I аннигиляционного излучения т. к. d ст ~ dP ~ Id Q, где dP — поток энергии излучения через площадь dS , интенсивность I = dP / dS . Причем это распределение связано только с импульсом электрона, угол 9 присутствует только в комплексе с импульсом p . В формуле (2) угловое распределение фотонов в явном виде отсутствует.

Во-вторых, формула (2) предполагает возможность различной энергии фотонов при аннигиляции, что запрещается выводом формулы (1) вследствие k i = - k 2 .

Поэтому прежде всего, возникает вопрос: какова природа углового распределения интенсивности аннигиляционного излучения в (1)? Связано ли это распределение с самим процессом аннигиляции, т. е. переходом «вещество – энергия», либо определяется какими-то другими эффектами? Сохранится ли данное угловое распределение фотонов при переходе к другой системе отсчета, например, связанной с позитронно-эмиссионным томографом?

2. Причины углового и энергетического распределения аннигиляционного излучения

Для исследования причины угловой зависимости дифференциального эффективного сечения (1) рассмотрим промежуточное выражение вывода, которое еще не просуммировано по направлениям поляризации фотонов [3]:

1      e ⁴

i28n² pk 0

х

f ( к 0 )          4 ( к 0 ) ( pe i ) 2 ( pe 2 ) 2

|^{( pk} i ) ^{( pk} 2 )       ( pk_i ) ² ( pk₂ ) ²

⁴ ( ^k 0 ) ( ^e i ^e 2 )( pe i )( pe 2 ) ( pk i )( pk 2 )

^{- ( e} i ^e 2 ⁾²

. d Q,

где k ₁ и k ₂ – импульсы фотонов. Переменные в квадратных скобках: импульс электрона, импульсы фотонов, единичные векторы поляризации фотонов записаны в виде 4-векторов.

Формулу (3) несложно преобразовать к виду: f 4

1      e ⁴

d ° =---2—n i28n2 pk0

-

i )( pk 2 )

- 2

+ ⁽ e i e 2 )

^ d Q.

-

2 ( _k 0 ) 2 ( pe i )( ^pe 2 ) ' ( pk i )( pk 2 )

Перейдем в (4) к пространственным векторам, используя правило ( ab ) = a ⁰ b ⁰ — ab , где a и b – трехмерные векторы, компоненты которых изменяются ковариантно, a ⁰ и b ⁰ – контравари-антно изменяющиеся компоненты 4-векторов, в нашем случае энергетические компоненты.

Переходя к трехмерным векторам, а также учитывая отсутствие контравариантных компо-

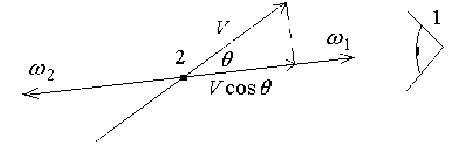
Рис. 1. Наблюдение фотонов, испускаемых движущимся источником

нент у поляризационных 4-векторов e ⁰ ражение (4) можно представить в виде

= 0, вы-

d а =

1 e ⁴

( к 0 ) ⁴

тривать как скорость движения позитрона. То же самое относится и к величине p в коэффициенте перед скобками. В данной системе отсчета формула (6) значительно упрощается:

—

—

128, 2 pk ⁰ [ ( к ⁰ ) ⁴— ( pk 1 ) 2

—

-12'

2 к 012 JPe l llPeLL + ( _e e ) ⁽⁾( к 0 ) 4 — ( Pk l ) 2

1 e ⁴

128n² pk ⁰

—

( pk-

[(к 0 )2 J

—

d а =

1 e ⁴

128п² рк ⁰

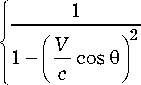
^— ( ^e 1 ^e 2 ) ^{d Q} . ⁽⁷⁾

^ d Q =

2 ( pe l )( pe 2 )

( к ⁰ ) ²

—

(       л2

^pk '

J к 0 )2 ,

,        . I2

+(eie2)

d Q.

При выводе (5) также использовано условие вылета фотонов в строго противоположных направлениях k 2 = — k 1 .

Учитывая |k 11 = к 0 , а также в соответствии с законом сохранения энергии ск ⁰ = тс ² (для наглядности вводим внутри скобок скорость света с = 1), в формуле (5) заменим

Исследуем вспомогательную задачу.

Наблюдатель 1, находящийся в «неподвижной» (связанной с Землей) системе отсчета, рис. 1, рассматривает некоторую движущуюся со скоростью V частицу 2, которая в определенный момент времени излучает два противоположно направленных кванта. При V = 0 частота квантов равна © 0 . Угол между скоростью частицы и направлением распространения одного из квантов равен 9. В направлении наблюдателя частица имеет составляющую скорости V cos 9.

За счет эффекта Доплера квант, движущийся в направлении наблюдателя, будет обладать повышенной частотой [6]:

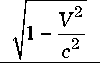
1--cos 9 c

pk ₁

( к ⁰ ) ²

— cos 9, c

где V – скорость электрона. В результате полу-

чим

d а =

e ⁴

-------Z--—  ------------------Z--

128л² рк ⁰< „ (V     Л 2

1 — I — cos 9

II с J

—

2---- (pejfp) +( e )   dq.

1—

Перейдем в (6) в лабораторную систему отсчета, предложенную в [4], связанную с электроном. В этом случае p = 0, а V — можно рассма-

Для кванта, движущегося в противоположном направлении, будет наблюдаться т. н. «красное

смещение»:

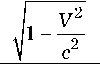
1 +— cos 9 c

Используя (8) и (9), найдем величину ком-

плекса © 1 / © 2 + © 2 / ® 1 + 2, который входит в

формулу (2):

(V    „)2

1 — I — cos 9 I

I с )

Отметим, что различие в частотах квантов в рассматриваемой задаче определяется различием в условиях наблюдения этих квантов: один

квант движется к наблюдателю, другой удаля-

ется от него.

В формуле (7) фактически реализуется рассмотренная вспомогательная задача. При этом под движущейся частицей подразумевается позитрон, а наблюдатель находится на «неподвижном» электроне. Поэтому, подставляя (10) в (7), найдем:

1       e ⁴

128п² 4 pk ⁰

х

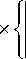
to 1

^to 2

—2 + ^{2 -} 4 ^{( e}1 ^e2 ^{) 2} to 1

d Q =

^{1     e 4} L ^(to 2 ^-to 1 ⁾²

I 1

128n² pk ⁰ I       4ГО 1 ® 2

Г d Q.

1 e ⁴

d ⁿ =--- 9 —i

128n² pk

= A J

128П 4 pk ⁰ I

11 Г to i 0 ⁰ [⁴ k^to 2

— + ² I - ( e i e 2 ) ^{2 to} 1 J

— + — + 2 - 4 ( e i e 2 ) 2 Г d Q. ^to 2     ^to 1

d Q =

Знак модуля принят вследствие стандартного использования модуля составного матричного элемента при нахождении дифференциального эффективного сечения процесса [2].

Отметим, что при использовании формулы (10) мы фактически отказались от условия ^k 2 = ^{- k} 1 -

Если в коэффициенте перед скобками в формуле (2) принять E ₊ = m = to i , то формулы (2) и (11) становятся тождественными.

Отметим еще один существенный момент, проявляющийся при переходе от системы отсчета, связанной с центром масс электрона и позитрона, к лабораторной системе отсчета, связанной с электроном. Если поделить формулу (9) на формулу (8), то получается результат, отличающийся от результата, полученного в монографиях, например, [7; 8].

При делении (9) на (8), принимая с = 1, получаем

3. Применение аннигиляционного излучения в позитронноэмиссионном томографе

Учитывая, что в позитронно-эмиссионном томографе скорости позитронов невелики, а также (8) и (9), можно записать:

^to 1 ^to 2

й

= ^to 0

-

V ² c ²

V

1 - I I cos² 9 к c J

” ^to 0 .

Подставляя (16) в (15), получим

1 e ⁴ I ₁ ( Ato ) ² 128n² pk ⁰ I      4to 0

> d Q ,

® 2 _ к 2 _ 1 — V cos 6 to = to " 1 + V cos 9 .

В [7; 8] предлагается следующее соотношение:

k 2 _ E ₊ - p ₊ cos 9

k 1        m

где обозначено Ato = to 2 - to 1 .

Найдем разность частот излучаемых фотонов, т. е. величину Ato = to 1 - К 2 используя формулы (8) и (9):

Учитывая E ₊ = m и p ₊ = mV , находим:

k ² = 1 - V cos 9.                               (14)

k 1

Ato = to0

V ²

У¹ c ²

V

1--cos 9

- to0

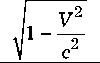
1 +--cos 9

c

c

Формула (14) несколько отличается от формулы (12). Это связано с тем, что формула (14) получена в рамках первого приближения теории возмущений. Поэтому она принципиально неточная. Формула (12) следует из точных формул эффекта Доплера. Таким образом, оставаясь только в рамках первого приближения те-

VV ²

2 — cos 9 1--5- c             c2

, Г V   ^²

1 - I — cos 9 I к c      J

.

Если угол 9 = 0 , т. е. позитрон движется по

линии, соединяющей детекторы у-излучения Д 1

ории возмущений невозможно установить эквивалентность формул (1) и (2).

и Д ₂, разность частот фотонов будет максималь-

но возможной и формула (18) преобразуется к

В заключение просуммируем формулу (11) по

виду

поляризациям фотонов. Возвращаясь к поляризационным 4-векторам с учетом e ⁰ = 0 и исполь-

2 ^V

^Ato max = ^to 0 I ^

.

Е ²

( ^е1 ^е2 ) = 2 [3], найдем:

e ₁, e ₂

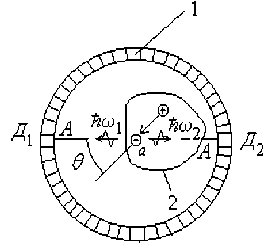
Рис. 2. Принципиальная схема регистрации фотонов в позитронно-эмиссионном томографе

Учитывая V << c , найдем:

A^ max ₌ V

.

2© 0      c

Величину ω₀ можно получить, исходя из приближенного равенства Йк> о ® mc ². В этом случае

Ato.     = 2 ^V ,                                      (21)

max , где

X = — = 3,86159 ■ 10 ^{- 13} м mc

– комптоновская длина волны электрона [10].

На рис. 2 показана принципиальная схема регистрации фотонов в позитронно-эмиссионном томографе [9].

Исследуемый объект 2 помещается в кольцо детекторов 1. При аннигиляции позитрона и электрона, находящегося в точке а , вылетают два кванта с энергиями Йо> 1 и h to 2 в противоположных направлениях (приведенная постоянная Планка Й = 1 введена для наглядности). Если кванты, летящие по линии А-А , регистрируются детекторами Д у и Д 2 одновременно, то точка испускания квантов находится посередине между детекторами Д 1 и Д 2 . Детекторы в кольце 1 с точки зрения эффекта Доплера в системе отсчета, связанной с электронами, играют роль неподвижных наблюдателей.

По количеству квантов, вылетающих в разных направлениях, процесс сферически симметричен. Поэтому плотность детекторов в кольце 1 должна быть равномерной. Однако частоты квантов, а следовательно, и их энергии, в зависимости от направления на детектор (наблюдатель) за счет эффекта Доплера могут различаться на величину ∆ω = ω2- ω1.

Регистрируя разность частот или энергий вылетевших в противоположных направлениях квантов, используя максимальное значение этой разности за время измерения ∆ωmax, можно оценить скорости движения позитронов (21). Учиты- вая, что скорость позитрона пропорциональна плотности ткани, через которую он движется р ~ V, получаем необходимую информацию о плотности ткани в патологическом очаге. Эта дополнительная информация может быть получена в процессе диагностики организма с помощью позитронно-эмиссионного томографа.

Заключение

По результатам проведенного анализа мы можем сделать следующие выводы.

Формулы (1) и (2) адекватно в разных системах отсчета описывают разлет фотонов при аннигиляции электрона и позитрона.

В лабораторной системе отсчета, связанной с электроном, угловое распределение количества вылетающих фотонов отсутствует, однако за счет различия в условиях наблюдения квантов, вследствие эффекта Доплера, возникает различие в частотах излученных квантов.

При переходе в систему отсчета, связанную с центром масс электрона и позитрона, различие в частотах излученных квантов редуцируется в угловое распределение интенсивности аннигиляционного излучения, которое также является следствием эффекта Доплера.

Исследуя угловое распределение интенсивности электромагнитного излучения при аннигиляции позитрона и электрона в системе их центра масс, мы исследуем не аннигиляцию, а совершенно другое физическое явление – эффект Доплера, который сопровождает аннигиляционное излучение. Следовательно, первая неисчезающая поправка теории возмущений, полученная на основе дырочной гипотезы Дирака, не приводит к подтверждению или отрицанию этой гипотезы, даже если эксперименты подтверждают угловое распределение интенсивности аннигиляционного излучения.

В лабораторной системе отсчета, связанной с позитронно-эмиссионным томографом, излучение аннигиляционных квантов сферически-симметрично, однако следует учитывать некоторое различие частот противоположно излученных фотонов вследствие эффекта Доплера.