Анализ архитектурных памятников Хорезма на основе особенностей фортификации

В настоящей работе предложен формальный метод оценки предназначения памятников на основе анализа их фортификационных особенностей. Известно довольно много примеров, когда с течением времени предназначение памятника изменяется. Каждое изменение сопровождается перестройками, при которых небольшие элементы, такие как бойницы, окна или коридоры, могут быть переделаны существенным образом по сравнению с изначальным планом. В этом случае провести оценку первоначального назначения сооружения по сформулированным критериям не представляется возможным.

В основе предлагаемого метода лежит геометрический анализ конфигурации расположения башен, предназначенных для защиты памятника. В принципе при реконструкции или перестройке памятника строители делали некоторые изменения, например они могли установить новую или снести старую башню. Однако ни одно из этих действий не останется незамеченным, поскольку существует множество материальных свидетельств подобных изменений. Например, на месте демонтированной башни можно обнаружить остатки старого фундамента, пристроенная часть сооружения может иметь другие геометрические размеры сырцового кирпича, а пахсовые фрагменты будут содержать частички керамики современного для пристройки периода. Таким образом, в большинстве случаев мы имеем представление о том, каким был памятник до реконструкции.

Данный метод может быть использован в качестве дополнительного критерия для определения предназначения памятника.

Методика анализа

В качестве основной гипотезы будем считать, что башни крепости или города несут в себе в первую очередь оборонительную функцию. Можно сделать эмпирическую оценку оптимального количества башен, которое необходимо и достаточно для эффективной защиты. С точки зрения обороны актуальным решением является расположение башен, обеспечивающих возможность флангового прострела соседних башен. Это означает, что башни должны находиться друг от друга на расстоянии, позволяющем вести прицельную стрельбу. Искомое оптимальное расстояние S_Onm может быть определено из анализа планов сооружений методами статистики.

Для оценки оптимального расстояния между башнями разделим архитектурные памятники Древнего Хорезма на два подмножества. В первую и наиболее многочисленную группу отнесем памятники, внешние стены или стены цитаделей которых представляют собой участки прямой. В большинстве случаев это четырехугольные сооружения, имеющие форму, близкую к квадрату (Анг-ка-кала, Кыркыз-кала), прямоугольнику (Джанбаз-кала, Калалы-гыр-1), ромбу (Аяз-3) или трапеции (Б. Гульдурсун). Однако мы можем рассмотреть и прямолинейные участки стен памятников, имеющих более сложную форму, например такие как Калалы-гыр-2.

Ко второй группе отнесем памятники круглой и эллипсоидальной формы. К сожалению, в Хорезме число таких сооружений измеряется единицами: Кой-Крылган-кала, Топрак-кала-Шаватская, Малый Кыркыз.

Анализ памятников четырехугольной формы. Для каждого памятника первой группы измерим длину стены (или ее фрагмента) X , количество башен N , укрепляющих данную стену, и вычислим среднее расстояние между башнями как: S = X / N. Получив в результате множество оценок среднего межбашенного расстояния S_i , после статистической обработки определим искомое оптимальное значение S_Onm . Все сооружения, у которых среднее межбашенное расстояние S_i значительно превышает оптимальное расстояние S_Onm , имеют худшие фортификационные характеристики и, следовательно, требуют отдельного рассмотрения.

Анализ памятников круглой формы. Аналогичным способом можно проанализировать памятники, форма которых близка круговой, представляет собой фрагмент (сектор) круга или эллипса. Зная длину окружности сооружения L и имея оценки оптимального расстояния S_Onm для четырехугольного памятника, можно оценить ожидаемое число башен n ₁ = L / S_Onm .

Для сооружений круглой формы необходимо ввести поправку, которая учитывает кривизну защитной стены сооружения. Очевидно, что при определенном соотношении числа башен и геометрических размеров сооружения соседние башни могут быть скрыты друг от друга внешней стеной сооружения. В этом случае фланговый прострел соседней башни окажется невозможным. При этом расстояние между ними может составлять SOnm. В работе (Болелов и др., 2015. С. 180) приведена оценка минимального количества башен n2, необходимых для обороны сооружения круговой формы:

п? =----------7------

² т       f R

2 • arccosI ( R + d

,

где R – радиус сооружения, d – длина стрелковой камеры внутри башни, откуда может вестись стрельба. Здесь необходимо сделать два замечания. Во-первых, в основу этой оценки положено, что башня выступает за окружность защитной стены. В противном случае, если башня является надстройкой над стеной, вести фланговый прострел соседних башен невозможно. Во-вторых, довольно часто башни сильно разрушены, и мы имеем оценку только их внешних размеров. Но и в этом случае, зная внешний размер и характерную толщину стены, можно сделать оценку размера стрелковой камеры внутри башни.

В результате оптимальное количество башен с точки зрения обороны находится из условия N_Onm = Max { n 1 ; n 2 }, где число n 1 вычисляется из оценки возможности ведения прицельной стрельбы, а число n ₂ – из условия возможности флангового прострела соседних башен. Методика поиска «нестандартных» сооружений состоит в сравнении оптимального (с точки зрения обороны) числа башен N_Onm с их реальным количеством N_Б . Очевидно, что при радиусе памятника порядка десятков метров оптимум будет определяться кривизной стены, т. е. через параметр n ₂. При радиусе памятника в сотни метров кривизна стены оказывается малой, и оптимум задается параметром n ₁.

Если числа N_Onm и N_Б соответствуют друг другу, следовательно, башни сооружения несут оборонительную функцию. Если же соотношение между N_Onm и N_Б нарушается в ту или иную сторону, это означает, что памятник имеет какие-то особенности, и он может быть интересен для последующего анализа.

Исходные данные

В качестве основного источника информации мы использовали археологические планы, опубликованные в трудах Хорезмской археолого-этнографической экспедиции. Для минимизации ошибок параметры X и N всегда определялись по наиболее хорошо сохранившейся стене или ее фрагменту. Если памятник сохранился хорошо, но для длины Д и ширины Ш получались немного разные величины S_Д и S_Ш , то для дальнейшего анализа использовалось усредненное значение ( S_Д + S_Ш ) / 2. В случае проведения процедуры усреднения межбашенного расстояния геометрический размер сооружения также усреднялся: X = Д + Ш .

Применяемая процедура определения среднего расстояния между башен, используя периметр или полупериметр сооружения, имеет свои плюсы и минусы. Недостаток состоит в том, что вместо реально измеренных расстояний мы используем некоторую среднюю величину, что делает невозможным поиск типового «модуля расстояния», который мог применяться при строительстве памятника. С другой стороны, при проведении статистического анализа каждый памятник должен учитываться однократно, а следовательно, его должен характеризовать единый параметр. В противном случае мы столкнемся с ситуацией, когда хорошо сохранившийся Аяз-кала-1 будет представлен в выборке 4 значениями (т. к. является четырехугольником), Калалы-гыр-2, имеющий форму сектора, – 2 значениями, а сохранившаяся Атсыз-кала – одним значением, которое характеризует ее наиболее целую стену.

С целью проверки и уточнения геометрических размеров стены мы воспользовались стандартным инструментом программы Google Earth (далее GE), которая позволяет измерять расстояние между заданными точками на спутниковом снимке.

Отметим, что все используемые исходные данные отягчены ошибками. Практика показала, что геометрические размеры памятника, измеренные в ходе полевых исследований, могут отличаться на 10–15 % от измерений, проведенных с помощью программы GE. В этом случае непонятно, какие данные являются более точными, особенно если исследуемый памятник сохранился (или виден на спутниковом снимке) не очень хорошо.

В результате мы составили выборку из 32 памятников (см. табл. 1), которые условно разбили на 3 периода: античные (до IV в. н. э.), раннесредневековые (V–IX вв. н. э.) и средневековые (X–XV вв. н. э.).

В эту выборку не были включены крепости, которые не имеют пристенных башен, например Джанбас-кала, Тешик-кала и т. д.

Анализ и интерпретация полученных результатов

На рис. 1, 1 показана зависимость среднего расстояния между башнями от длины сооружения. Кружками обозначены памятники античного периода, треугольниками – сооружения раннего средневековья, звездочками – объекты средневековья.

Из рисунка следует, что с увеличением длины стены (геометрических размеров памятника) Х расстояние между башнями Y также возрастает вплоть до значения X ≈ 200 м. Это означает, что сооружения, которые имеют небольшие геометрические размеры (например, цитадели), в среднем укрепляются большим количеством башен, чем крупные объекты. Основная часть значений Y находится в диапазоне 20–30 м.

При размерах крепостной стены X > 200 м среднее расстояние между башнями перестает зависеть от Х и находится в пределах 30–40 м. То есть для протяженных памятников принцип «чем длиннее стена, тем больше расстояние между башнями» не работает. Вероятно, что интервал расстояний 20–40 м есть оптимум межбашенного расстояния с точки зрения фортификации. При этом для памятников с размерами до X < 200 м оптимальное расстояние находится в диапазоне 20–30 м, а для крупных X > 200 м – 30–40 м. Из общей закономерности выбиваются точки, которые соответствуют памятникам Большой Гуль-дурсун, Кангка-кала и Ярбекир-кала.

В дальнейшем мы рассмотрим эти сооружения отдельно, а пока, считая эти три объекта памятниками с особенностями, исключим их из анализа. Кроме того, для удобства анализа и наглядности рисунка удалим из рассмотрения Калалы-гыр-1. Это единственный объект в данной выборке, размеры которого превышают 400 м. Тем не менее отметим, что межбашенное расстояние на Ка-лалы-гыр-1 составляет около 30 м, что соответствует параметрам основной группы памятников.

Таблица 1

№	Объект	Фрагмент	Источник	Оценка
Памятники античного периода (до IV в. н. э.)
1	Ангка-кала	любая стена: 87 м – 3б	GE; ( Толстов , 1948. С. 114)	43,5 м
2	Аяз-кала-1	сев. стена: 143 м – 8б вост. стена: 170 м – 9б зап. стена: 172 м – 9б	GE	20,5 м 21,5 м
3	Аяз-кала-3	южн. стена: 245 м – 9б	GE; ( Болелов , 1998. С. 117)	30,5 м
4	Базар-кала	с.-в. стена цит.: 117 м – 4б	GE; ( Толстов , 1948. С. 112)	30 м
5	Гульдурсун	сев. cтена: 310 м – 4б южн. стена: 265 м – 4б	GE; ( Толстов , 1948. Рис. 106)	103 м 88 м
6	Гяур-кала на Чермен-ябе	зап. стена цит.: 67 м – 4б фрагм. южн. стены: то же	( Толстов , 1948. С. 116)	17 м
7	Гяур-кала Султан Уиз-даг	сев. cтена: 162 м – 8б	( Толстов , 1948. С. 119)	23 м
8	Казакли-Яткан	сев. стена цит.: 324 м – 12б	GE	29,5 м
9	Калалы-гыр-1	фрагм. зап. стены: 500 м – 17б	( Толстов , 1948. С. 80); (МХЭ-6. С. 142)	31,25 м
10	Калалы-гыр-2	вост. стена: 192 м – 6б зап. стена: 202 м – 6б	(Калалы-гыр-2, 2004. Рис. 2/4)	38,4 м 40,4 м
11	Канга-кала	фрагм. с.-з. стены: 88 м – 2б фрагм. с.-в. стены: 44 м – 2б	(МХЭ-1. С. 28)	88 м 44 м
12	Капарас	вост. cтена: 90 м – 4б южн. стена: 75 м – 4б	(ДЮХ. С. 156)	30 м 25 м
13	Кош-кала-1	зап. стена: 78 м – 5б Длина найдена из плана	( Ершов , 1941. С. 185)	19,5 м
14	Кургашин-кала	с.-в. стена: 130 м – 5б	GE; ( Толстов , 1948. С. 111)	32,5 м
15	Кыркыз Бол.	сев. стена: 211 м – 7б зап. стена: 228 м – 8б	GE	35 м 32,5 м
16	Хазарасп (цит.)	сев. стена: 300 м – 7б	(МХЭ-6. С. 158)	50 м
Раннесредневековые памятники (V–IX вв. н. э.)
1	Беркут-кала	зап. стена: 92 м – 4б зап. стена: 105 м – 4б	GE; ( Толстов , 1948. С. 136)	21 м 31,3 м
2	Итаксан-кала	фрагм. зап. стены: 31 м – 2б	GE	31 м
3	Кош-Парсан	сев. стена: 76 м – 4б	GE	25 м
4	Кум-Баскан-кала	длина цит.: 125м – 5б ширина цит.: 110 м – 5б	( Толстов , 1948. С. 136)	31,3 м 22 м
5	Кум-кала	сев. стена: 164 м – 5б	( Толстов , 1948. С. 151)	41 м

Окончание таблицы 1

Раннесредневековые памятники (V–IX вв. н. э.)
6	Пиль-кала	вост. стена цит.: 51 м – 5б фрагм. южн. стены: 100 м – 6б	( Толстов , 1948. С. 124)	13 м 20 м
7	Уй-кала	ширина 1: 113 м – 4б ширина 2: 100 м – 3б	( Толстов , 1948. Рис. 136)	37,7 м 50 м
8	Якке-Парсан	зап. и вост. стены: 68 м – 4б	( Толстов , 1948. С. 125); (МХЭ-7. С. 3)	21 м 22,5 м
Средневековые памятники (X–XV вв. н. э.)
1	Бештам-кала	сев. стена: 134 м - 5б	(МХЭ-4. Рис. 10)	33,5 м
2	Буран-кала-1	сев., южн. стены: 37 м – 3б зап., вост. стены: 33 м – 3б	( Толстов , 1948. С. 154)	18,5 м 16,5 м
3	Даудан-кала	южн. стена: 125 м – 5б	( Толстов , 1948. С. 162)	31,3 м
4	Дая-Хатын	сев., зап., южн. стены: 118 м – 5б	( Ершов , 1941. С. 187)	29,5м
5	Кават-кала	зап. стена: 175 м – 5б	(МХЭ-1. С. 151; ( Толстов , 1948. С. 170)	43,5 м
6	Наиб-кала-1	сев. cтена: 44 м – 3б вост. cтена: 56 м – 3б	( Толстов , 1948. С. 151)	22 м 28 м
7	Наиб-кала-2	сев. стена: 39 м – 3б	( Толстов , 1948. С. 151)	19,5 м
8	Ярбекир-кала	с.-з. стена: 220 м – 3б	(МХЭ-6. Рис. 42)	110 м

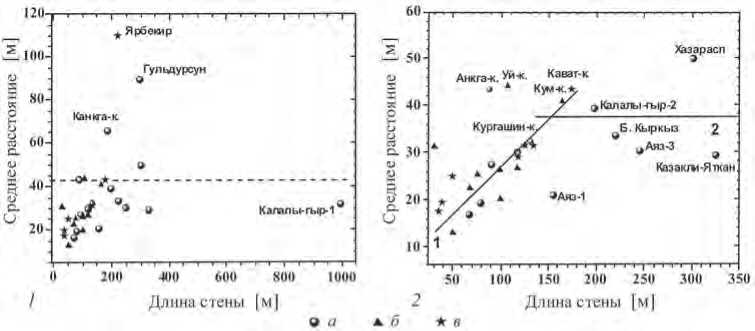
Рис. 1. Зависимость среднего расстояния между башнями от длины стены сооружения

• 1    – по всей выборке; 2 – то же, после исключения из выборки четырех «нестандартных» памятников. Условные обозначения: а – памятники античного периода; б – сооружения раннего средневековья; в – объекты средневековья

Рис. 1, 2 показывает, что значимых отличий в укреплении стен башнями в сооружениях античности, раннего средневековья и позднего средневековья не обнаруживается. С завершением периода античности исчезают крупные памятники, меняются приемы и каноны фортификации, но средняя величина межбашенного расстояния остается прежней.

Детализированный рис. 2 позволяет уточнить сформулированные ранее результаты. Расположение памятников на графике можно попытаться аппроксимировать в рамках разных моделей. Рассмотрим модель, в которой данные оцениваются двумя линейными регрессиями вида Y = a + bX . При небольших размерах сооружения X ~30 м, которые соответствуют форту или цитадели крепости, межбашенное расстояние увеличивается вместе с возрастанием параметра Х , вплоть до «точки поворота» X = 140 ÷ 200 м. На графике этому соответствует прямая № 1. Затем межбашенное расстояние перестает зависеть от Х и стабилизируется на уровне Y ~30–40 м, чему соответствует прямая № 2.

Точка поворота характеризует момент, когда среднее расстояние между башнями перестает зависеть от размера памятника Х . Памятники, которые описываются прямой № 1, будем условно считать «обычными», а те, которые характеризует прямая 2, – «крупными». В качестве разделительного рубежа в первой модели выберем значение X ≈ 140 м, а во второй – X ≈ 200 м. В результате этого три памятника Аяз-кала-1, Кум-кала и Кават-кала будут относиться к разным выборкам. Поскольку вторая группа насчитывает малое число объектов, оценка параметров прямой № 2 может значительно измениться.

Результаты расчетов представлены на рис. 2, 1 и 2 .

Согласно расчетам, в обоих случаях коэффициенты уравнения прямой № 1 практически одинаковы. Для первой модели a ₁₁ = 15,97 ± 4,54 и b ₁₁ = 0,124 ± 0,049 при коэффициенте детерминации R ₁ ² ₁ = 25,89, а для второй a ₂₁ = 16,04 ± 3,70 и b ₂₁ = 0,121 ± 0,033 при R ₂ ² ₁ = 37,12¹. Аналогичная ситуация наблюдается для прямой № 2, где имеем значения коэффициентов a ₁₂ = 37,33 ± 7,53 и b = 0,006 ± 0,015 при R ² = 4,57 и a = 34,55 ± 4,84 и b = -0,00023 ± 0,0128 12                                      12                   22                              22

при R ₂ ² ₂ = 2,01. Из t-статистики следует, что коэффициенты b ₁₂ и b ₂₂ незначимы, поэтому ими можно пренебречь.

Если в выборе модели опираться на коэффициент детерминации, то небольшое преимущество имеет модель № 2. В первой модели уравнение прямой № 2 вычисляется всего по 5 точкам, и коэффициент а имеет почти вдвое большую ошибку. Проблема с определением коэффициентов регрессии для прямой № 2 присутствует в обоих случаях. Она связана с тем, что «крупных» памятников мало. Если вдруг найдется пара «крупных» памятников, результат может измениться в пользу той или иной модели. Поэтому в данном случае нельзя сделать однозначный выбор.

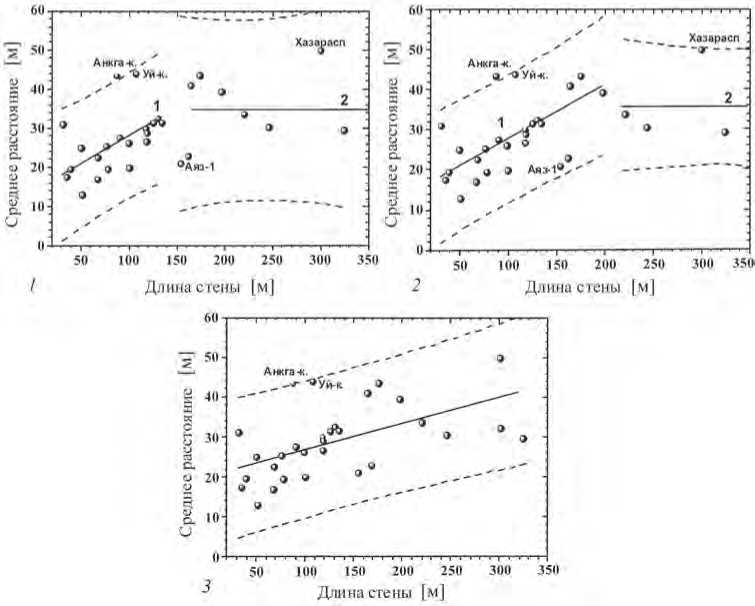
Рис. 2. Моделирование фортификации памятников

1 – модель 1. Положение точек на графике аппроксимировано двумя линейными регрессиями с точкой поворота при Х = 140 м;

• 2    – модель 2. Положение точек на графике аппроксимировано двумя линейными регрессиями с точкой поворота при Х = 200 м;

• 3    – модель 3. Положение точек на графике аппроксимировано единой линейной регрессией

Для обеих моделей регрессионная зависимость № 1 дает примерно одинаковые оценки межбашенного расстояния в диапазоне значений от 16 до 35 м. Регрессия № 2 также приводит к одинаковым значениям среднего расстояния a ≈ 36 м, но имеет разные оценки погрешности, которые соответственно равны σ _a ¹ ≈ 8м и σ _a ² ≈ 5 м. Тогда минимальные и максимальные оценки среднего расстояния между башнями при доверительном интервале 2σ составляют a _min ≈ 200 a _min ≈ 22–25 м и a _Max ≈ 45–52 м.

Наконец, рассмотрим третью модель, где все значения аппроксимируем одним уравнением, а удаленную точку X = 990 м, которая соответствует Калалы-гыр-1, исключим из анализа (рис. 2, 3 ).

В результате получим оценки а ₃ = 21,53 ± 2,87 и b ₃ = 0,058 ± 0,018 при R 32 = 26,3. Отметим, что в данном случае коэффициент b статистически значим, и мы предполагаем, что величина среднего расстояния между башнями Y медленно возрастает с ростом X . На наш взгляд, гипотеза постоянного роста Y ( X) является неудачной, а сама идея нелогичной. Например, по этой модели межбашенное расстояние на Калалы-гыр-1 должно быть около 86 м, а на самом деле оно составляет 31 м. Тем не менее все три рассмотренные модели отражают определенные тенденции.

Как мы уже упоминали выше, размеры памятников измерены с ошибками. Сравнение археологических планов с измерениями, сделанными в программе GE, в ряде случаев дает соответствие, а в ряде – рассогласование. Это означает, что погрешность, с которой мы находим исходные параметры, отлична для разных памятников. Следовательно, в наших исходных данных присутствует ге-тероскедастичность, искажающая оценки коэффициентов регрессии a и b . Хотя ошибка межбашенного расстояния коррелирует с ошибкой измерения размера памятника, устранить гетероскедастичность не получится, поскольку мы имеем перекрестные оценки геометрических размеров только для некоторых памятников.

Анализ «нестандартных» памятников

Одной из целей построения модели среднего межбашенного расстояния было выявление для последующего изучения «нестандартных» памятников, которые значимо отклоняются от общей закономерности. Рассмотрим три памятника, которые были исключены из рассмотрения в самом начале анализа. Это Кангка-кала, Большой Гульдурсун и Ярбекир-кала.

Крепость Кангка-кала находится на крутом холме, о чем можно судить по изолиниям уровня (рис. 3). Расстояние между парой башен № 1 и № 2 на северо-западной стене составляет около 88 м. Однако на расстоянии 20 м от стены уровень поверхности снижается на 7 м, поэтому атаковать такую стену сложно, и с точки зрения фортификации в данном случае число башен является достаточным для успешной обороны. Северо-восточный склон имеет меньший наклон, который наиболее крут возле угловой башни № 3. Около башни № 3 уровень снижается на 4 м на расстоянии 14 м от башни. Поэтому расстояние между этими башнями вдвое меньше, чем между парой башен № 1 и № 2, и составляет около 45 м, что является стандартом для «крупных» сооружений. Сохранность этого памятника не позволяет проанализировать фортификацию его других стен. Однако проведенный анализ двух сохранившихся стен позволяет установить, что количество башен и, соответственно, межбашенное расстояние зависят от крутизны холма, на котором расположен памятник.

Аналогичный прием фортификации применен на Кыз-кале, расположенной на обрыве. Ее стены не имеют башен, за исключением северо-западной стены, склон которой более пологий. Северо-западная стена укреплена тремя башнями ( Толстов , 1948. Рис. 168). Адаптацию расположения башен под рельеф местности можно проследить на Кургашине. Восточный и западный углы крепости укреплены парами башен в форме ласточкиного хвоста. Южная башня расположена рядом с обрывом, поэтому башня, укрепляющая ее, смещена вдоль стены к северо-западу ( Толстов , 1948. С. 111).

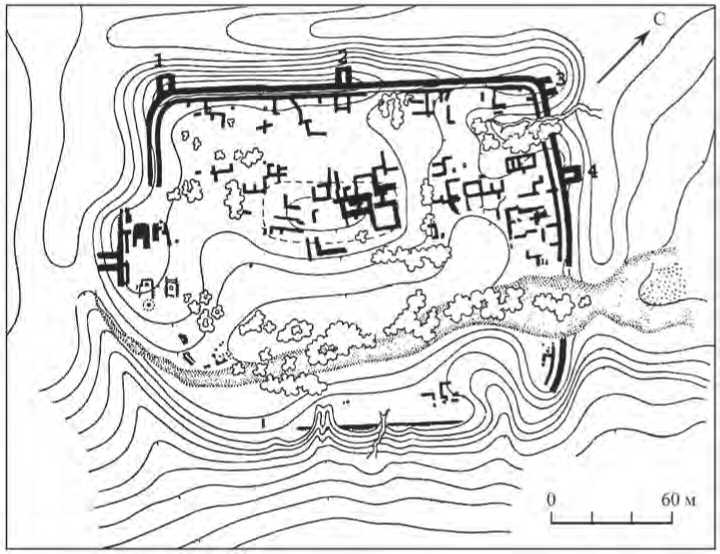
Рис. 3. Топографический план крепости Кангка-кала (по: Толстов , 1962. С. 228)

Большой Гульдурсун. Античное сооружение, датируемое IV–III вв. до н. э., сохранилось до средневековья, когда крепость подверглась существенной модернизации. Внутренняя часть стрелковой галереи была срезана, а внешняя стена укреплена толстым пахсовым слоем. В связи с этим старые бойницы потеряли свою актуальность и были замазаны. Стены протяженностью около 280–300 м были укреплены четырьмя башнями, две из которых находились по углам. Учитывая, что стены наращивались с внешней стороны, возможно, что конфигурация башен также была изменена. Однако у нас нет сведений на этот счет.

Памятник Ярбекир-кала изучен довольно мало. Здесь не производилось раскопок до 1958 г., когда был заложен лишь один шурф. Фортификационные сооружения Ярбекир-калы датируются периодом XII–XIII вв. Судя по обнаруживаемым культурным слоям кангюйского и кушанского периодов, это место было обжито давно. Мы не имеем достаточной информации по данному памятнику, чтобы попытаться объяснить аномально малое количество башен. Также мы не располагаем топографическим планом с линиями уровня горизонта, поэтому не можем применить рассуждения, как на Кангка-кале и Кыз-кале.

Крепости Ангка-кала и Уй-кала имеют примерно вдвое большее межбашенное расстояние, если их сравнивать с памятниками аналогичного размера.

Рис. 4. Фотография города Хазарасп из программы Google Earth

дятся на небольшом холме высотой в

Во всех трех моделях Уй-кала находится на границе диапазона объяснимого отклонения, а Ангка-кала немного выпадает из него. Тем не менее с точки зрения фортификации среднее расстояние между башнями на них такое же, как на Кум-кале, Кават-кале и Калалы-гыр-2. Поэтому, хотя они не являются «типовыми» в нашем понимании, мы не можем утверждать, что эти крепости укреплены недостаточно надежно.

Две из трех моделей показывают относительно малое количество башен на Хазараспе. Судя по фотоснимкам (рис. 4), крепостные его стены нахо-несколько метров, поэтому можно пред- положить, что «недостаток» количества башен компенсируется естественным рельефом местности. Однако всегда можно найти и другое объяснение. Как мы уже упоминали, существуют памятники, которые не были укреплены башнями вообще. Расположение стены цитадели Тешик-калы в нескольких метрах от крепостной стены бессмысленно с точки зрения обороны. Это значит, что мы не всегда можем получить ответ на основе методов оптимизации.

Также представляет интерес памятник античного периода Аяз-кала-1, который при размерах ~ 150 м, согласно всем моделям, имеет среднее межбашенное расстояние, характерное для памятников размером 30–100 м. В результате на Аяз-кале-1 мы имеем «избыточное» количество башен. Возможно, это связано с расположением крепости, которая обороняла внешние границы Хорезма с северо – северо-востока. Увеличенное число башен обеспечивает более высокую линию соприкосновения с неприятелем, а следовательно, позволяет задействовать дополнительное количество бойцов.

Анализ памятников круглой формы

Применим нашу методику к памятникам круглой формы, расположенным на территории Хорезма, в фортификации которых присутствуют башни.

Кой-Крылган-кала. Согласно измерениям ( Лапиров-Скобло , 1979), диаметр внешней оборонительной стены Кой-Крылган-калы составляет 176 м. В рамках принятой классификации памятник относится к категории крупных. Тогда получим оценку параметра n 1 в диапазоне от п х 176 / 48 = 11,76 до п х 176 / 22 = 25,13, или, после округления, n ₁ = 12 ÷ 25. В действительности Кой-Крылган-ка-ла имеет 9 башен, чему соответствует среднее расстояние между башнями около 61 м. Следовательно, по критериям, определенным выше, Кой-Крылган-калу следует считать «сооружением с особенностями».

Расположение башен Кой-Крылган-калы уникально, поскольку в отличие от всех рассмотренных ранее памятников они находятся над стеной, а не выступают за нее. Поэтому фланговый прострел межбашенного пространства невозможен в принципе и значение параметра n ₂ для Кой-Крылган-калы не может быть определено.

Оба этих фактора свидетельствуют в пользу того, что башни Кой-Крылган-калы не имеют фортификационного значения, а выполняют иную функцию ( Бо-лелов и др. , 2015. С. 181).

Топрак-кала Шаватская. По данным ( Мамбетуллаев , 1986. С. 12), диаметр сооружения составляет 260 м. Наше измерение, сделанное с помощью стандартных инструментов программы GE, подтверждает эту оценку. Тогда оптимальный диапазон параметра n 1 находится в пределах n 1 = 17 ^ 37. Если предположить, что внутреннее свободное пространство верхней части башни примерно соответствовало геометрическим размерам нижней камеры d = 2,0 ^ 2,5 м, то получим оценку n ₂ = 16 ^ 18. С точки зрения фортификации оптимальное число башен должно находиться в диапазоне N = Max { n 1 ; n 2 } = Max {17 ÷ 37; 16 ÷ 18} = 18 ÷ 37. Согласно археологическому плану, на памятнике имеется B = 24 башни, что соответствует оптимальному диапазону с точки зрения обороны. При этом среднее расстояние между башнями составляет 34 м. Отсюда следует, что башни Топрак-калы Шаватской выполняют оборонительную функцию.

Эрес-кала. Памятник античности Эрес-кала имеет неправильную форму ( Толстов , 1948. Рис. 117), однако всю его восточную стену можно рассматривать как фрагмент окружности с радиусом кривизны около R ≈ 260 м. С помощью рис. 5 можно определить, что расстояние между парами соседних башен составляет около 35 м. Эта величина соответствует оценке оптимума межбашенного расстояния для крупных памятников.

Башни Эрес-калы имеют форму вытянутой половинки эллипса, далеко выступающей за стену. Возможность флангового прострела пространства между соседними башнями видна непосредственно из плана сооружения. Поэтому башни Эрес-калы носят оборонительную функцию.

На территории Хорезма мало памятников круговой или эллиптической формы. С формальной точки зрения к ним можно было бы еще отнести Малый Кыркыз и Чильпик. Однако на этих памятниках не обнаружены башни, поэтому данный метод анализа использовать нельзя.

Применение данной методики к памятникам круговой (эллиптической) формы показывает, что башни Кой-Крылган-калы носят декоративный характер. Это интересный результат, поскольку принято считать, что Кой-Крылган-кала является (или, точнее сказать, считается) культовым центром, а наша методика выявляет эту особенность.

Памятник Топрак-кала Шаватская вызывает интерес тем, что относится к редкому для Хорезма типу памятников круговой формы. Кроме того, он хронологически синхронен Кой-Крылган-кале, которая считается культовым центром. М. Мамбетуллаев утверждает, что археологические исследования 1979–1980 гг. не дали материалов для окончательного решения вопроса о его функциональном значении ( Мамбетуллаев , 1986. С. 46). В связи с этим автор выдвинул гипотезу, что форма памятника обусловлена некими космогоническими идеями, а сам памятник связан с солярным культом и мог являться храмом Солнца или огня (Там же. С. 46–47).

Согласно нашему анализу, конфигурация башен Топрак-калы Шаватской носит фортификационный характер и типична для крепостей. Полученный результат

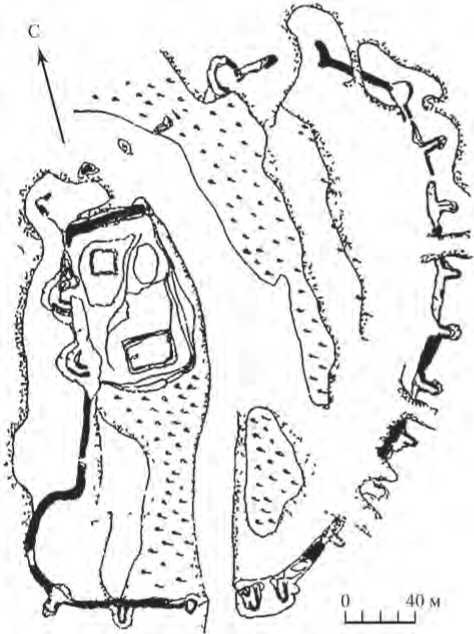
Рис. 5. Археологический план крепости Эрес-кала (по: Толстов , 1948. С. 58)

не позволяет сделать окончательный вывод о функциональном назначении памятника, а является лишь одним из критериев оценки.

Определение модуля расстояния

В архитектуре модулем расстояния является унифицированная мера длины, которая заложена в основе всех конструкций памятника. Нашей задачей является определение возможного стандарта меры длины, который определял расстояние между башнями сооружения. Как мы уже упоминали выше, основной сложностью для решения этой задачи является не всегда хорошая точность исходных данных. Только для некоторых памятников мы имеем перекрестные наземные измерения, а реальная точность оценок расстояний, выполненных с помощью инструментов GE, нам неизвестна.

Кроме того, несмотря на возможное наличие стандарта, строители могли сделать неправильную разбивку памятника, совершить другие ошибки, которые искажают результат в ту или иную сторону. Однако при наличии достаточно большого количества данных ошибки усредняются, что открывает возможность поиска модуля расстояния.

Заново составим таблицу средних межбашенных расстояний, но в отличие от предыдущего случая не будем проводить усреднений. Кроме того, прямоугольный памятник будет характеризоваться в выборке не одним числом, а двумя. Например, северная стена Аяз-калы-1 имеет длину 143 м и укреплена 8 башнями, а западная и восточная при длине около 171 м защищены 9 башнями. Средняя длина между башнями составляет в этом случае 20,4 м и 21,4 м. Эти стены можно было бы укрепить 8 башнями и получить расстояние 24,4 м, которое вполне соответствует нашему оптимуму.

В результате обработки данных табл. 1 мы построили две частотные гистограммы (рис. 6). Каждая гистограмма показывает, насколько часто встречается в выборке диапазон расстояний, который соответствует данному каналу (интервалу). В обоих расчетах мы приняли ширину канала равной 2,5 м (h = 2,5 м), а отличие формы частотных профилей объясняется разными точками отсчета. Именно по причине вариации частотного профиля в зависимости от начала отсчета и ширины канала и были построены две гистограммы.

Из рис. 6 можно выделить три ярко выраженных максимума, которые примерно соответствуют расстояниям Y ~ 20 м, 30 м, и 40 м, что кратно 10 м. Значению Y = 50 м соответствует небольшой пик, который задается только двумя памятниками (Хазарасп и Уй-кала), поэтому наличие четвертого максимума нельзя доказать статистически. Однако отметим, что если конфигурация первых трех максимумов неслучайна, то именно в этом месте должен быть расположен следующий экстремум.

Зато, используя метод средневзвешенного центра, мы можем сделать предварительную оценку положения максимумов № 1 – № 3 по формуле x=

f m + 1        A / m + 1

x ,

x=|Z v Ш \ m-1        // m-1

где x_m есть положение центра канала (столбика) и f_m – значение его частоты, а числа в суммах означают, что центр определяется по двум соседним столбцам. В результате найдем значения x 1 = 22,3 м, x ₂ = 30,9 м и x ₃ = 41,3 м, откуда следует значение модуля расстояния M ≈ 10 м.

Опираясь на полученные результаты, можно уточнить положение максимумов. При определении средневзвешенного центра мы теряли точность, когда заменяли истинное значение межбашенного расстояния значением, которое соответствует центру канала. Теперь в качестве центров максимумов возьмем определенные ранее x , а границы каналов определим диапазоном x ± 1,5 h . В результате для максимумов № 1 – № 3 получим границы интервалов [18,55; 26,05], [27,15; 34,65] и [37,55; 45,05], после чего вычислим средние арифметические значения величин y по значениям табл. 1, которые попадают в соответствующие диапазоны. В результате получим уточненные оценки положения максимумов: x 1 = 21,9 ± 1,9 м, x ₂ = 31,1 ± 1,2 м и x ₃ = 41,2 ± 2,5 м.

По причине наличия ошибок, совершенных архитекторами при составлении планов памятников, и наших ошибок, допущенных при нахождении размеров с помощью планов, улучшить полученный результат не представляется возможным.

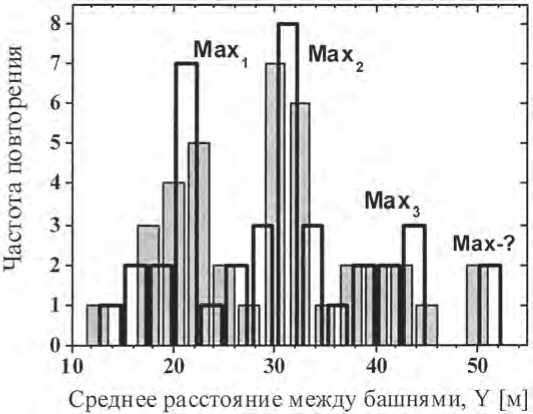
Рис. 6. Определение модуля расстояния. Частотная гистограмма, характеризующая количество памятников с заданным межбашенным расстоянием

Заключение

Проведенный анализ показывает, что в период с античности до средневековья значимого отличия в планировке укрепления сооружений башнями не обнаруживается. При этом мы допускаем, что могли изменяться каноны построения башен – форма, конструкция, конфигурация бойниц и внутренних помещений, однако эти детали не являются предметом настоящего исследования. Можно утверждать, что плотность расположения башен с течением времени не менялась.

Крупные памятники с размером от ~ 150 м и больше имеют в среднем одну башню на 36 м длины стены, а вариация этого значения от памятника к памятнику не превышает 15–20 % данной величины. Для более компактных памятников характерно меньшее расстояние между башнями, которое может быть приближенно оценено с помощью уравнения вида Y = 16 + 0,123 х Х .

Обратим внимание на определенные нами модельные параметры α = 16, β = 0,123 и γ = 36. Набор коэффициентов (α, β, γ) может являться инвариантным только для памятников Хорезма или отражать фортификационные особенности сооружений Средней Азии в целом. Этот вопрос может быть предметом отдельного исследования.

Анализ соотношения длины крепостной стены с количеством башен позволяет заподозрить наличие унифицированного модуля расстояния, который составлял около 10 м в современной мере длины. Получить более точную оценку с помощью имеющихся в нашем распоряжении данных не представляется возможным.

В средневековом Хорезме использовалась мера длины – газ. По источникам известны две меры длины: «земельный газ» – 106–107 см и «текстильный»

газ – мера, которой измерялись ткани, – 61 см. Земельными газами измерялась и площадь. Так, один танаб – общепринятая единица площади в Средней Азии – в Хорезме равнялся 3600 кв. газов, по 60 газов на стороне. Нет никаких сомнений, что эта мера длины появилась задолго до эпохи средневековья, возможно, такие же меры, но под другим названием использовались и в эпоху античности. Во всяком случае, можно предполагать, что 10 м, или приблизительно 10 газов, и были тем самым модулем, который использовался при строительстве не только средневековых крепостей, но и более ранних фортификационных сооружений. Полученные модели межбашенного расстояния позволяют выявлять памятники с «нестандартным» числом башен с целью их дальнейшего изучения.