Анализ чувствительности параметров модели скольжения колёс автономного транспортного средства

DOI:

В настоящее время системы управления роботизированных транспортных средств обладают сложной архитектурой [1-3]. Для того чтобы алгоритмы верхнего уровня управления обладали высокими показателями эффективности, а также могли выполнять задачи тактического уровня, необходимо проводить тестирование на специальных цифровых моделях, которые позволяют охватить наиболее распространённые сценарии поведения в автономном режиме. Процесс торможения является одним из важнейших режимов динамики автономного мобильного объекта. Системы управления тормозами относятся к системам активной безопасности. В данной работе была описана подсистема управления скольжением колёс в составе антиблокировочной системы (далее по тексту: АБС), работа была проведена в программной среде GNU Octave.

Задачей АБС является поддержание ведомого или ведущего колёс в режиме оптимального относительного скольжения Л, при котором коэффициент сцепления шины р с опорной поверхностью получается максимальным.

Были построены частотные характеристики динамики скольжения колёс в зависимости от распределения нагрузки и различных значениях скорости.

МАТЕРИАЛЫ И МЕТОДЫ

За основу численной модели продольной динамики автомобиля была рассмотрена схема расстановки сил, представленная на рис. 1.

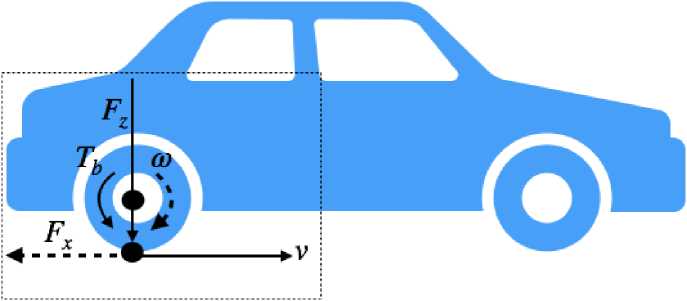
Рисунок 1. Одномассовая упрощённая модель.

Figure 1. Single-mass simplified model.

Список исходных данных приведён в таблице 1. Рассмотрим на численной модели, как влияет скорость транспортного средства и распределение вертикальной нагрузки на

динамику скольжения. Все четыре колеса рассматриваются как динамически развязанные, что означает, что динамические явления передачи нагрузки, вызванные креном, не были включены в модель. Зависимость сил трения от вертикальной нагрузки моделируется как пропорциональная зависимость. Однако это предположение справедливо только в статических условиях.

Была построена одномассовая модель автомобиля, изолированная часть которой, отражена на рис. 1 может быть рассмотрена как:

(JW = rF x — T_b

( mv = —Fx , где w (рад/с) - угловая скорость колеса; v (м/с) - продольная скорость центра масс автомобиля; Ть (Нм) - тормозной момент; Fx (Н) - продольная сила, приложенная в точке контакта колеса с дорогой; / (кг м2) - момент инерции колеса одномассовой модели; m (кг) - масса автомобиля для упрощённой модели; г (м) - радиус колёс соответственно. Линейное торможение колеса представляет собой уравнение (2)

toT

^ =-- s

Далее было использовано соотношение между нормальной силой и продольной силой, полученное как описание продольной силы связи «колесо-дорога».

F x = Fz^A)

Графики зависимости коэффициента сцепления от продольного скольжения колеса при различных дорожных условиях приведены в открытом доступе. Основой такой зависимости для асфальтобетонного покрытия был график.

Подставив (2) в (1), была получена системы уравнений (4).

(JW = rFzF (^Д

V-toT mv = —Fz^ (—

—

Ть>

)'

где динамика скольжения колеса и его угловой скорости представляют собой:

Л = —Lw+^v; V      V2

w=V(1 — Л).

Таблица 1. Список основных исходных данных для моделирования.

Table 1. List of main input data for modeling.

Параметр	Значение	Параметр	Значение
Л	0,05	V	25, м/с
Т	700, Н • м	Fz	m^ д,Н
тип дорожного полотна	асфальтобетонное покрытие	тип   дорожного полотна	асфальтобетонное покрытие

На основе вышеизложенного материала был проведён анализ характеристик одномассовой модели (1), вычислена точка равновесия, выполнена линеаризация модели согласно подходу, изложенному Sergio M. Savaresi [4]. Далее была определена передаточная функция от тормозного момента по отношению к проскальзыванию колес (5).

г

G^s) =

/У

где ^и(Л) - зависимость коэффициента сцепления от скольжения.

Распределение вертикальной нагрузки описывается с помощью соотношения (6):

N = —

тд

В АБС наиболее часто осуществляется управление по двум переменным: замедлению скорости и пробуксовке (проскальзыванию) колеса. Пример представления структуры подсистемы управления коэффициентом скольжения представлен ниже на рис. 2. Задающим значением будет желаемый коэффициент скольжения Я * , управляющим воздействием тормозной момент Т_ь , выходным сигналом является фактическое значение коэффициента скольжения. В качестве алгоритма управления для простого случая применяется регулятор класса ПИД.

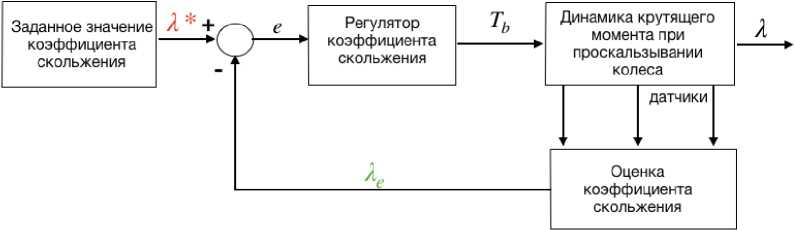
Рисунок 2. Упрощённая структурная схема управления коэффициентом скольжения.

Figure 2. Simplified block diagram of slip coefficient control.

В процессе проектирования инженер может рассмотреть степень влияния изменений параметров системы на её поведение. В идеале изменения параметров, вызванные внешней средой или другими причинами, не должны оказывать заметного влияния на производительность системы. Необходимо провести анализ чувствительности параметров системы на примере одномассовой модели продольной динамики транспортного средства. Для получения частотных характеристик при анализе чувствительности параметров модели были использованы совмещённые графики логарифмических амплитудно-фазовых частотных характеристик (диаграммы Боде).

РЕЗУЛЬТАТЫ

Рассчитаны в программной среде GNU Octave и проанализированы диаграммы Боде для иллюстрации динамической зависимости модели от скорости автомобиля v и вертикальной нагрузки F_z (рис.3 и рис.4).

Обращаясь к результатам моделирования можно сказать, что распределение вертикальной нагрузки влияет на низкочастотную составляющую, в то время как изменение скорости на высокочастотную составляющую диаграмму Боде. Это означает, что на вид переходного процесса в большей степени влияет распределение нагрузки.

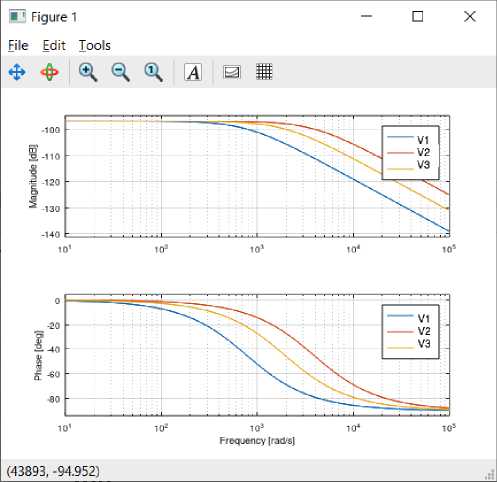
Рисунок 3. Диаграмма Боде для системы G ^ (s) при параметрах скорости V 1 = 25 м/с, v₂ = 10 м/c, v₃ = 5 м/c.

Figure 3. Bode diagram for the system GA(s) with speed parameters v, 25 m/s, v2=10 m/s, v3 =5 m/s.

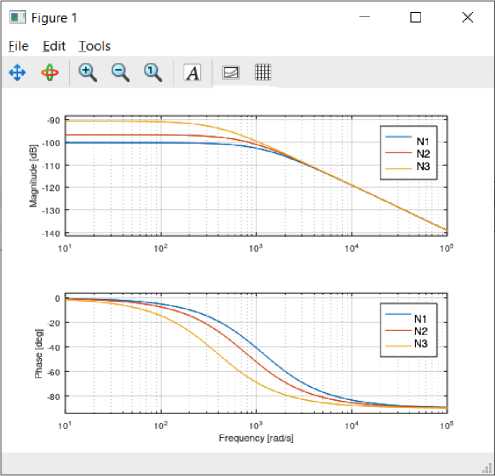
Рисунок 4. Диаграмма Боде для системы G ^ (s) при параметрах распределения вертикальной нагрузки N 1 = 0,5, N 2 = 1 м/c, N₃ = 1,5.

Figure 4. Bode diagram for the system G ^ (s)with vertical load distribution parameters N 1 =0.5, N 2 =1 m/s, N₃=1.5.

ОБСУЖДЕНИЕ

Как следует из анализа чувствительности параметров системы: при увеличении вертикальной нагрузки на колёса уменьшается запас устойчивости по амплитуде, а при увеличении скорости v оказывается масштабирующий эффект в области значений. Что требуется учесть для проектирования системы управления при различных условиях [5, 6].

Наиболее распространённый подход заключается в регулировании одной переменной, и чтобы другая переменная оставалась в пределах заранее определенных пороговых значений. В современных системах управления существует ряд методов, которые позволяют осуществлять управление одновременно по двух каналам.

ЗАКЛЮЧЕНИЕ

Полученные результаты и выводы позволяют осуществить попытку исследования влияния параметров на систему, описывающую динамику торможения роботизированного мобильного объекта. С точки зрения теории управления, наиболее целесообразным будет применить алгоритм многосвязного управления к данной системе.