Анализ действия закона Гибрат в городах России

Автор: Манаева Инна Владимировна

Журнал: Региональная экономика. Юг России @re-volsu

Рубрика: Фундаментальные исследования пространственной экономики

Статья в выпуске: 3 т.8, 2020 года.

Бесплатный доступ

Зарубежные исследователи проводят апробацию закона Гибрат на примере фирм, регионов и стран. Важность эмпирического подтверждения данного закона заключается в том, что он позволяет определить, имеет ли население города, региона или страны в целом общий путь роста и существует ли между ними единичная зависимость размера. Актуальность данного исследования определяется необходимостью расширения показателей для оценки роста городов с применением закона Гибрат в современных российских условиях. Цель статьи - проанализировать выполняемость закона Гибрат в городах России по показателям: численность населения города, плотность населения в городе, среднегодовая численность работников предприятий в городе, среднемесячная заработная плата в городе, число предприятий и организаций на территории города, а также определить целесообразность использования данного закона для городских систем России. В Уральском, Сибирском и Дальневосточном федеральных округах (2009-2016 гг.), в Северо-Западном, Приволжском, Сибирском и Дальневосточном федеральных (2016-2018 гг.) округах темп роста городов не зависит от их первоначального размера. Также закон Гибрат был подтвержден для показателя плотности населения в городе в 2009-2016 гг. в Сибирском федеральном округе, в 2016-2018 гг. - для всех федеральных округов, кроме СКФО; для показателя среднегодовая численность работников предприятий в городе в Южном (2003-2009 гг., 2009-2016 гг.), Уральском (2009-2016 гг.), Сибирском (2009-2016 гг.), Северо-Западном (2016-2018 гг.), Северо-Кавказском (2016-2018 гг.) и Дальневосточном (2016-2018 гг.) федеральных округах. Для показателя среднемесячной заработной платы в городе в Сибирском федеральном округе в 2009-2016 гг.; в Центральном, Северо-Западном и Уральском федеральных округах в 2016-2018 годах. Для показателя числа предприятий и организаций на территории города в Южном федеральном округе в 2009-2016 гг.; в Северо-Кавказском, Приволжском, Уральском и Сибирском федеральных округах в 2016-2018 годах.

Еще

Пространственная экономика, рост городов, закон гибрат, федеральный округ, численность населения, плотность населения, среднегодовая численность работников, среднемесячная заработная плата, число предприятий и организаций, города России

Короткий адрес: https://sciup.org/149131998

IDR: 149131998 | DOI: 10.15688/re.volsu.2020.3.5

Текст научной статьи Анализ действия закона Гибрат в городах России

DOI:

В области экономики города динамика численности населения и закономерности распределения размеров городов являются предметом активных исследований мирового экономического сообщества в течение последних десятилетий. Зарубежная научная литература сфокусирована на том, чтобы показать, применяется ли закон Гибрат эмпирически. Согласно данному закону население городов растет случайным образом с одинаковым средним и дисперсией, существует независимость между темпом роста населения и размером города. Важность подтверждения данной эмпирической закономерности заключается в том, что она позволяет определить, имеет ли население города, региона или страны в целом общий путь роста и существует ли между ними единичная зависимость размера, что позволяет прогнозировать развитие городов и влияние на них внешних шоков. Если численность населения является стационарной, можно заключить, что внешние шоки временны, и город вернется на свой долгосрочный путь развития. В ситуации, когда последствия внешних потрясений являются постоянными либо долгосрочными, численность популяции оказывается нестационарной. В более ранних исследованиях мы применяли закон Гибрат для оценки роста городов России [Манаева, 2016; Manaeva, 2019; Иванова, 2008]. Актуальность данного исследования определяется необходимостью расширения показателей для оценки роста городов с применением закона Гиб-рат в современных российских условиях.

Цель статьи – проанализировать выполня-емость закона Гибрат в городах России по показателям: численность населения города, плотность населения в городе, среднегодовая численность работников предприятий в городе, среднемесячная заработная плата в городе, число предприятий и организаций на территории города, а также определить целесообразность использования данного закона для городских систем России.

Литературный обзор

В 1931 г. Р. Гибрат в исследовании фирм отметил, что их рост не зависит от размера, и распределение фирм по размеру приближается к логарифмически нормальному распределению. Из этих результатов вытекает так называемый закон Гибрат или закон пропорционального роста, который в случае городов устанавливает, что независимо от их размера они растут случайным образом с одинаковым ожидаемым значением и одинаковой дисперсией [Gibrat, 1931].

Закон Гибрат эмпирически проверяется с использованием статистического и динамического подходов. Статистический подход предполагает группировку фирм по их первоначальному размеру, далее проводится группировка на квартили и оценка темпов роста каждого квартиля. Закон Гибрат подтверждается, когда нет существенных различий в темпах роста между группами. В современных исследованиях используется динамический подход, который включает в себя определение степени влияния предыдущего темпа роста фирмы (города) на текущий рост.

В ряде исследований было обнаружено, что рост городов не соответствовал закону Гибрат. Проводя оценку системы городов в Англии в XIX в., Б. Робсон обнаружил, что средние темпы роста с размерами и отклонениями городов снижаются с увеличением размера города [Robson, 1973]. Более поздние исследования городов во Франции и Японии подтверждают закон

Гибрат [Eaton, Eckstein, 1997]. В модифицированной модели Гибрат число городов увеличивается, когда мигранты, приходя в город, образуют новый с вероятностью π , либо следуют в существующий город с вероятностью 1 – π [Simon, 1955]. Возможность выбора имеющегося города пропорциональна его размеру, как показано в законе Гибрат. Модель Х. Саймона способна генерировать степенной закон с показателем 1/(1 – π ). Когда π очень мало, то есть возможность возникновения нового города мала, модель способна генерировать закон с показателем, очень близким к закону Ципфа.

Данные методы были рассмотрены в стохастических моделях К. Габаикса, который утверждал, что данный закон представляет собой случайный процесс роста, который позволяет объяснить одну из наиболее важных статистических закономерностей в экономике городов – закон Ципфа [Gabaix, 1999]. Закон Гибрат – это случайный процесс, при котором доля города i в численности всего городского населения страны в период t отмечаeтся P _i _, _t , в период t – 1 умножается на γ _i _, _t , где γ _i _, _t – одинаково и независимо распределено по городам и времени [Gabaix, 1999].

^Pi , t ^{= γ} i , t^Pi , t - 1 . (1)

Экономические модели роста городов базировались на балансе преимуществ и издержках агломерации [Allen, Sanglier, 1979; Carruthers, Mulligan, 2007; Partridge et al., 2008]. Ряд моделей предполагают схожие определяющие факторы, которые имеют фундаментальное значение для понимания сложной динамики, лежащей в основе городских иерархий [Eeckhout, 2004; Gonzáles-Val et al., 2013].

Чтобы проверить эмпирическую значимость закона Гибрат, С. Кларк и Ж. Стаблер рекомендуют использовать модульное тестирование корня [Clark, Stabler, 1991]. Базовый тест корневого модуля Дики-Фуллера можно сформулировать следующим образом:

Δ ln P i , t =β it ln P it +ε it . (2)

Закон Гибрат выполняется при γ _{i t} = 1. Наличие корня, равного единице, свидетельствует о том, что рост городов зависит от внешних факторов.

А. Лаланне и М. Зумпе показывают, что случайный рост городов может соответствовать двум версиям закона Гибрат с противоположными значениями для коинтеграции и конвергентного пове-

дения [Lalanne, Zumpe, 2015]. Г. Перес и А. Рока, тестируя закон Гибрат на городах Колумбии за период 1835–2005 гг., заключили, что в начале XIX в. и первой половине XX в. рост городов зависел от численности их населения. На динамику численности населения оказывало влияние размещение отраслей производства. Начиная с 30-х гг. XX в. рост населения городов Колумбии перешел к новой модели, совпадающей с прогнозами закона Гибрат: города росли с одинаковой скоростью независимо от их размера [Pérez, Roca, 2013]. Б. Оке апробировал закон Гибрат относительно размера фирм и провел оценку взаимосвязи с их ростом в Нигерии [Oke, 2018]. Ученый заключил, что размер фирмы предсказывает их рост в Нигерии на уровне значимости 5 %, что противоречит закону Гибрат. В исследовании показано, что небольшие фирмы растут быстрее, чем крупные.

Из числа современных российских ученых по тематике исследования целесообразно отметить В.В. Андреева и В.Ю. Лукиянову, работы которых посвящены тестированию закона Гиб-рат в населенных пунктах Приволжского федерального округа [Андреев, Лукиянова, 2015; Андреев, Лукиянова, Кадышев, 2017]. Н.К. Пирогов и М.Г. Поповидченко применяют закон Гиб-рат для оценки роста предприятий. Ученые заключают, что закон Гибрат является приемлемой гипотезой для зрелых и крупных предприятий, данный закон не работает в отношении молодых фирм [Пирогов, Поповидченко, 2010].

Данные и методы

Для проверки выполняемости закона Гиб-рат в работе применяется следующая формула:

ln r i , t =β 0 +γ 1 ln r i , t - 1 , (3)

где β ₀ – константа; r _i _, _t – численность населения города i в год t ; r _i _, _t _–1 – численность населения города i в год t –1; если γ ₁ равен 1, то темп роста города и начальный размер независимы (закон Гибрата выполняется) [Chesher, 1979].

Характеристики коэффициента γ ₁ [Chesher, 1979]:

γ ₁< 1 – темп роста малых городов выше темпа роста крупных;
γ ₁ > 1 – темп роста крупных городов выше темпа роста малых [Chesher, 1979].

Для проведения исследования была сформирована выборка, в состав которой вошли населенные пункты, имеющие статус города, численностью населения более 100 тыс. человек. Слабо развитая муниципальная статистика, отсутствие ряда статистических показателей для городов численностью населения менее 100 тыс. чел. не позволяют включить их в данную работу. Анализируемые показатели: численность населения города, плотность населения в городе, среднегодовая численность работников предприятий в городе, среднемесячная заработная плата в городе, число предприятий и организаций на территории города. Период исследования: 2003 г., 2009 г., 2016 г., 2018 год. Оценка проводилась для городов в границах федеральных округов. Источником информации послужили данные Федеральной службы государственной статистики.

Закономерности распределения городов в границах федеральных округов РФ

Рассмотрим особенности распределения городов в границах федеральных округов РФ согласно их размерам (табл. 1).

В границах федеральных округов Российской Федерации наблюдается дисбаланс в размерах городов. Наибольшее количество городов имеет численность населения менее 100 тыс. чел.: в ЦФО – 85 %, СЗФО – 93 %, ЮФО – 81 %, СКФО – 75 %, ПФО – 84 %, УФО – 85 %, СФО– 84 %, ДВФО – 85 %. В Российской Федерации нет городов с численностью населения от 2 000 до 5 000 тыс. человек. Проведенный анализ показал отрыв Москвы (12 108,3 тыс. чел.) и Санкт-Петербурга (5 132 тыс. чел.) от остальной группы городов.

Обнаруженная дифференциация обостряет социально-экономические проблемы регионов РФ ввиду того, что неравномерная система подвержена влиянию негативных факторов (внешнеэкономические, политические, экологические) и развитию нестабильности в обществе.

В данном исследовании проводится анализ по ряду социально-экономических показателей. Численность населения и плотность населения являются индикаторами успешности развития города. Фактором, определяющим выбор места жительства трудоспособного населения, является наличие рабочих мест, уровень оплаты труда которых удовлетворяет требованиям работников. Величина среднемесячной заработной платы обусловливает уровень материальной обеспеченности трудоспособного населения и является одним из критериев привлекательности города. Число предприятий и организаций на территории города определяет масштабы и успешность хозяйственной деятельности города.

На рисунках 1–5 представлены иерархии десяти городов-лидеров по анализируемым показателям.

Таким образом, за анализируемый период заметен процесс роста численности населения городов, г. Москва, г. Санкт-Петербург, г. Новосибирск и г. Ростов-на-Дону сохраняют свои позиции в иерархии. На более высокие позиции поднялись г. Екатеринбург (с пятой на четвертую), г. Казань (с восьмой на шестую), г. Челябинск (с девятой на седьмую). Более низкие позиции заняли г. Самара (с шестой на седьмую – 2009 г., на девятую – 2016 г.), г. Омск (с седьмой на восьмую).

Наблюдается неоднозначная картина по анализируемому показателю. Значение показателя первого города в иерархии снижается на 32 %. Все города меняют свои позиции. Из иерархии лидеров выбывают города Владимир, Химки, Ковров, Сергиев Посад с 2009 года. Показатель плотности населения в городе изменчив в Московской области, что объясняется миграцией населения и растущей московской агломерацией.

Таблица 1

Распределение размеров городов по федеральным округам РФ, 2017 г.

Величина города, тыс. чел.	ЦФО	СЗФО	ЮФО	СКФО	ПФО	УФО	СФО	ДВФО
≥ 10 000	1	–	–	–	–	–	–	–
5 000–10 000	–	1	–	–	–	–	–	–
2 000–5 000	–	–	–	–	–	–	–	–
1 000–2 000	1	–	2	–	5	2	3	–
500–1 000	3	–	2	1	7	1	5	2
250–500	12	5	2	3	5	7	2	2
100–250	27	4	9	10	15	11	11	6
≤ 100	262	137	64	42	166	118	109	56
Количество городов	306	147	79	56	198	139	130	66

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

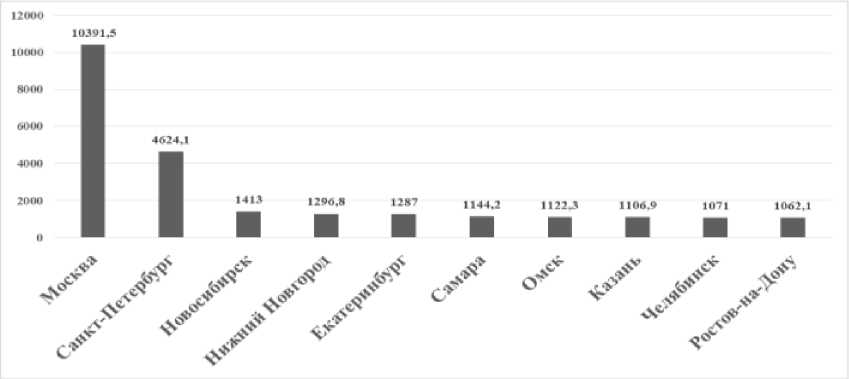
а) 2003 г.

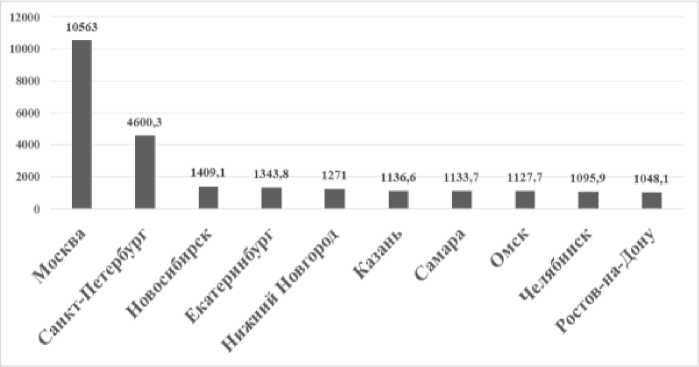
б) 2009 г.

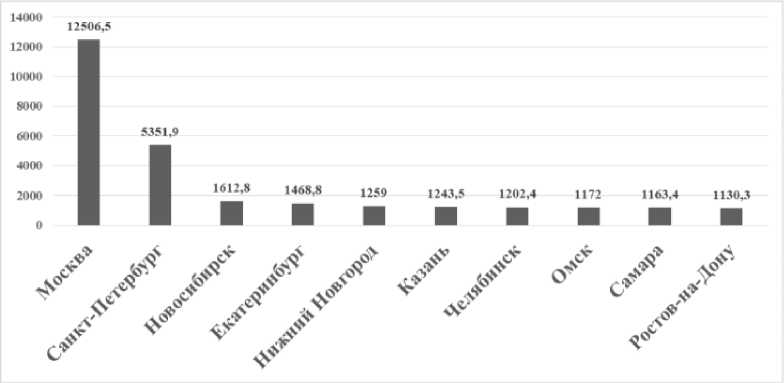
в) 2016 г.

Рис. 1. Иерархия городов-лидеров России по численности населения, 2003–2018 гг., тыс. чел. (см. также с. 54) Примечание. Рассчитано по данным Федеральной службы государственной статистики.

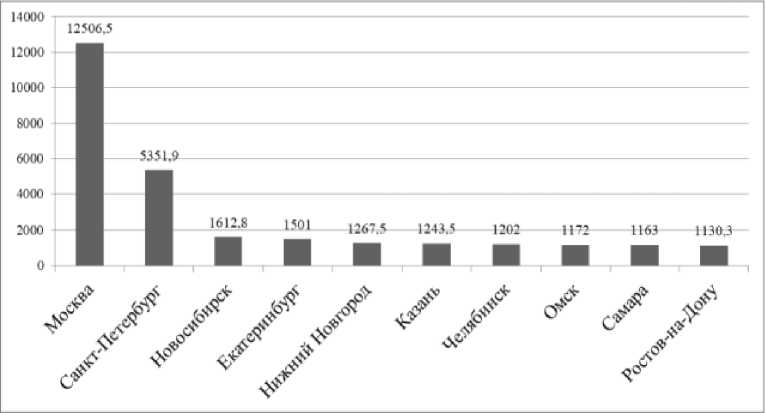
г) 2018 г.

Рис. 1. Окончание

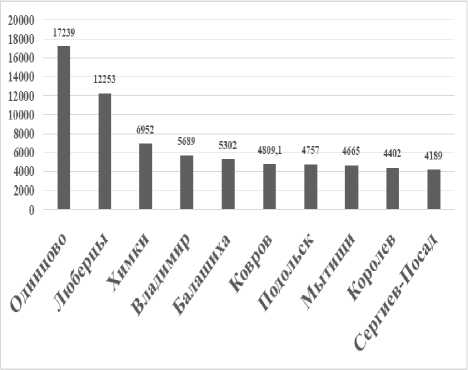
а) 2003 г.

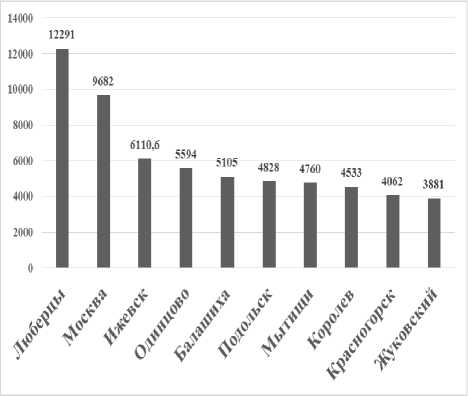
б) 2009 г.

Рис. 2. Иерархия городов-лидеров по показателю плотности населения в городах России, 2003–2018 гг., чел./км2 (см. также с. 55)

Примечание . Рассчитано по данным Федеральной службы государственной статистики.

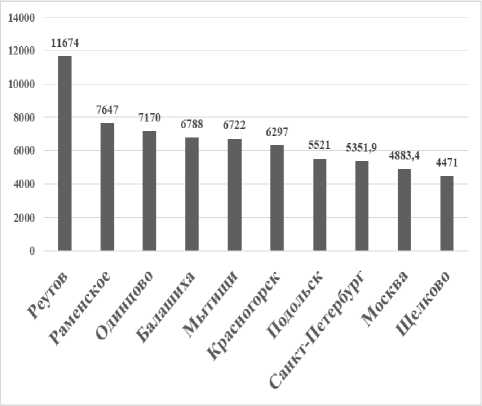
в) 2016 г.

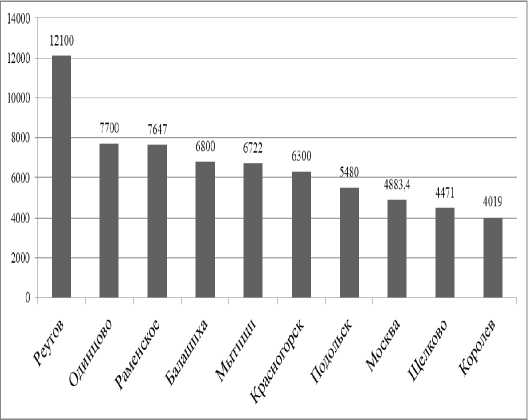
г) 2018 г.

Рис. 2. Окончание

а) 2003 г.

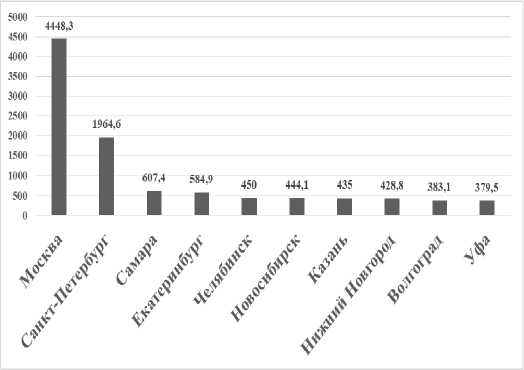
Рис. 3. Иерархия городов-лидеров России по среднегодовой численности работников предприятий, 2003–2018 гг., тыс. чел. (см. также с. 56)

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

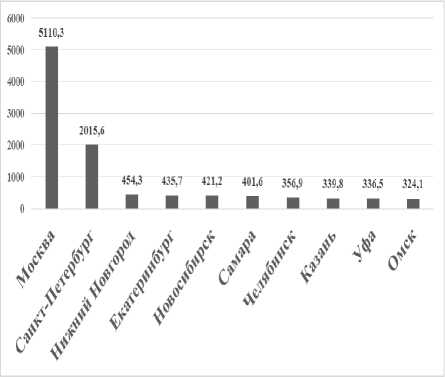
б) 2009 г.

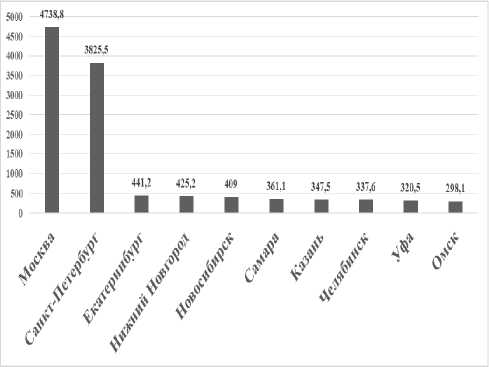
в) 2016 г.

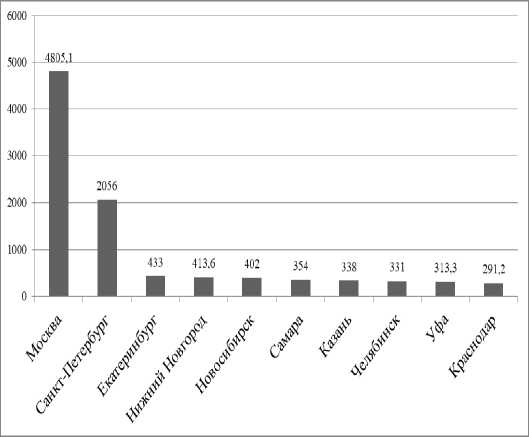
г) 2018 г.

Рис. 3. Окончание

а) 2003 г.

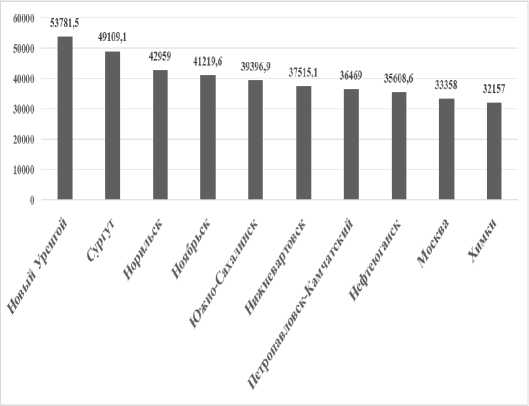
б) 2009 г.

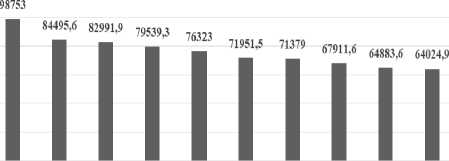
в) 2016 г.

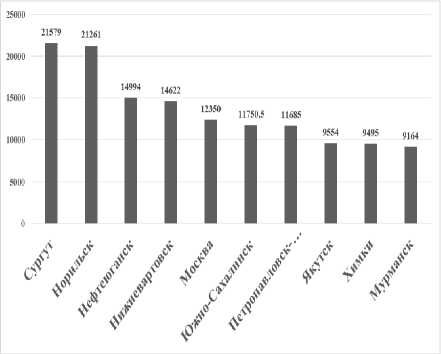
Рис. 4. Иерархия городов-лидеров России по показателю среднемесячной заработной платы в 2003 (см. также с. 58)

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

2018 гг., руб.

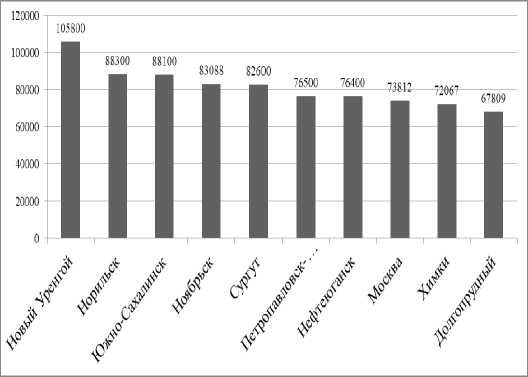
г) 2018 г.

Рис. 4. Окончание

а) 2003 г.

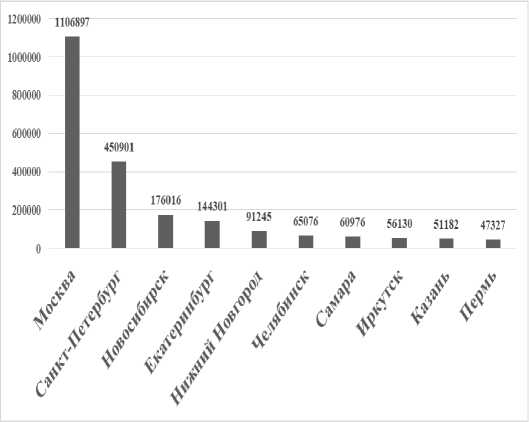
б) 2009 г.

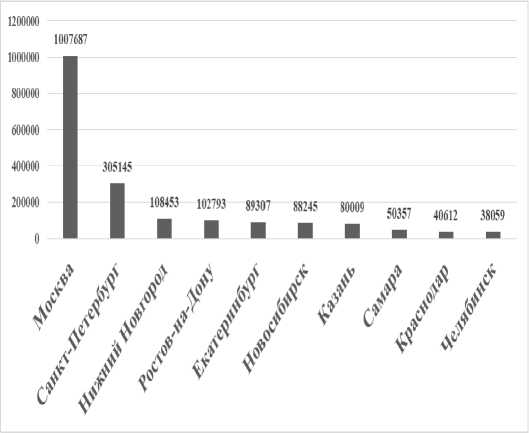
Рис. 5. Иерархия городов-лидеров России по числу предприятий и организаций, 2003–2018 гг., ед. (см. также с. 59) Примечание. Рассчитано по данным Федеральной службы государственной статистики.

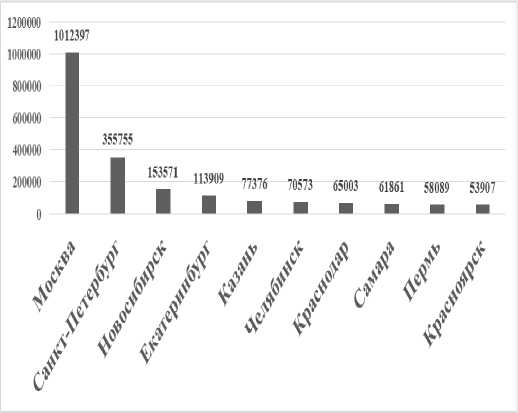
в) 2016 г.

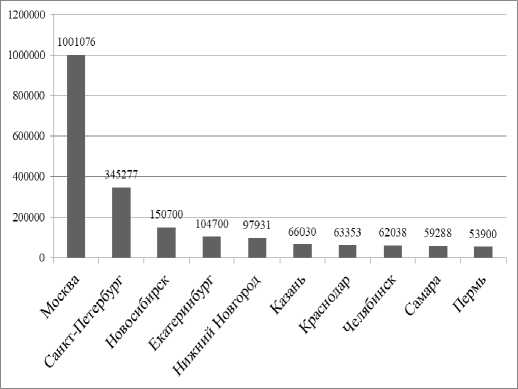
г) 2018 г.

Рис. 5. Окончание

По показателю среднегодовой численности работников предприятий в городе наблюдается схожая ситуация с показателем численности населения в городе (рис. 1), что логично и предсказуемо. Имеет место отрыв Москвы и Санкт-Петербурга от остальной массы городов. Снижение позиций характерно для Самары, Челябинска – с 2009 г., Волгограда – с 2018 года. Омск выбывает из десятки городов-лидеров. Более высокие позиции заняли Екатеринбург, Новосибирск, Уфа – с 2009; г. Краснодар в 2018 г. вошел в десятку городов-лидеров.

В десятку городов-лидеров по показателю среднемесячной заработной платы входят горо-да-«нефтяники», г. Москва и города Дальневосточного федерального округа. В 2016 г. на восьмую позицию поднялся г. Химки, на десятую – г. Долгопрудный. С 2009 г. г. Новый Уренгой стал занимать первую позицию, а г. Сургут опустился на четвертую позицию. Таким образом, можно констатировать высокие темпы роста среднемесячной заработной платы в г. Новый Уренгой. Необходимо отметить, что для получения объективной картины качества жизни в городе целесообразно проводить оценку доли прожиточного минимума в среднемесячной заработной плате, что станет предметом будущих исследований.

Данные рисунка 5 демонстрируют, что г. Нижний Новгород, г. Ростов-на-Дону с 2009 г. выбывают из десятки городов-лидеров. Позиции повышаются у г. Новосибирск, г. Екатеринбург, г. Челябинск. Неоднозначная ситуация наблюдается в отношении г. Краснодар в 2009 г.: он выбывает из лидеров, а в 2016 г. и 2018 г. занимает седьмую позицию. В 2018 г. в иерархию городов-лидеров по данному показателю вошел г. Нижний Новгород, занял пятую позицию, г. Красноярск выбыл из десятки лидеров.

Тенденции роста анализируемых показателей в городах России

В таблицах 2–6 представлены результаты оценки роста анализируемых показателей с применением закона Гибрат.

При оценке показателя численности населения в городах России в период 2003–2009 гг. получен оценочный коэффициент от -0,4 до 0,3, таким образом, закон Гибрат в этот период не выполняется.

За 2009–2016 гг. получен оценочный коэффициент, равный единице, в Уральском, Сибирском и Дальневосточном федеральных округах, то есть можно заключить, что на их территории темп роста обследуемых городов не зависит от их первоначального размера. На территории Центрального и Приволжского федеральных округов темпы роста малых городов выше темпов роста крупных. В Северо-Западном, Южном и Северо-Кавказском федеральных округах закон Гиб-рат не выполняется.

За 2016–2018 гг. на территории Северо-Западного, Приволжского, Сибирского и Дальневосточного федеральных округов темп роста не зависит от первоначального размера (оценочный коэффициент равен единице). На территории Центрального, Южного и Северо-Кавказского федеральных округов темп роста малых городов выше темпа роста крупных. На территории Уральского федерального округа наблюдается противоположная картина: крупные города растут быстрее малых.

Как демонстрируют данные таблицы 3, закон Гибрат по показателю плотности населения в городе за период 2003–2009 гг. не выполняется.

За 2009–2016 гг. оценочный коэффициент по анализируемому показателю в Сибирском федеральном округе равен единице, что подтверждает вы-полняемость на его территории закона Гибрат. Темп роста плотности населения в менее населенных городах выше, чем в густонаселенных городах в Центральном, Приволжском и Уральском федеральных округах. Противоположная ситуация складывается в Северо-Кавказском федеральном округе. В Северо-Западном, Южном и Дальневосточном федеральных округах закон Гибрат не выполнялся.

За 2016–2018 гг. на территории всех федеральных округов, за исключением Северо-Кавказского, закон Гибрат выполняется. Отметим, что за данный период существенных изменений показателя плотности населения в обследуемых городах не произошло.

При оценке показателя среднегодовой численности работников предприятий в городе оценочный коэффициент, равный единице, получен в Южном федеральном округе за два периода исследования, в Уральском и Сибирском федеральных округах за 2009–2016 гг., что свидетельствует о выполняемости закона Гибрат.

В Центральном, Северо-Кавказском и Приволжском федеральных округах в 2009–2016 гг. темп роста среднегодовой численности работников предприятий в малых городах выше, чем в крупных.

За 2016–2018 гг. в Южном федеральном округе закон Гибрат не выполняется. На территории Северо-Западного, Северо-Кавказского и Дальневосточного федеральных округов рост среднегодовой численности работников предприятий не зависит от первоначальных значений данного показателя. В остальных федеральных округах темп роста среднегодовой численности работников предприятий в малых городах выше, чем в крупных.

По данным таблицы 5 можем заключить, что за 2003–2009 гг. слабое действие закона Гибрат наблюдается на территории Южного федерального округа, где темп роста среднемесячной заработной платы в городах с низкими значениями данного показателя выше. В остальных федеральных округах закон Гибрат не выполняется. В 2009– 2016 гг. оценочный коэффициент, равный единице, получен в городах Сибирского федерального округа. В Северо-Кавказском и Приволжском федеральных округах в 2009–2016 гг. темп роста среднемесячной заработной платы в городах с низкими значениями данного показателя выше.

За 2016–2018 гг. в Южном и Приволжском федеральных округах закон Гибрат не выполняется. В городах Центрального, Северо-Западного и Уральского федеральных округов темп роста среднемесячной заработной платы не зависит от первоначального значения данного показателя. В городах Северо-Кавказского, Сибирского и Дальневосточного федеральных округов оценочный коэффициент ниже единицы, таким образом, темп роста среднемесячной заработной платы в городах с низкими значениями данного показателя выше.

Данные таблицы 6 демонстрируют, что по анализируемому показателю в 2003–2009 г. на территории Южного федерального округа темп роста новых предприятий и организаций в малых городах выше (оценочный коэффициент 0,9). На территории остальных федеральных округов закон Гибрат не выполняется.

За период 2009–2016 гг. в Южном федеральном округе наблюдается выполняемость закона Гибрат. В четырех федеральных округах (СЗФО, СКФО, УФО, СФО) полученный оценочный коэффициент подтвердил, что темп роста новых предприятий и организаций в малых городах выше.

За 2016–2018 гг. оценочный коэффициент, равный единице, получен в Северо-Кавказском,

Приволжском, Уральском и Сибирском федеральных округах. На территории Южного федерального округа закон Гибрат не выполняется. На территории Центрального, Северо-Западного и Дальневосточного федеральных округов темп роста новых предприятий и организаций в малых городах выше.

Таблица 2

Коэффициенты линейного уравнения оценки закона Гибрат по показателю «численность населения» в городах России в 2003–2018 гг.

Показатели	ЦФО 1	СЗФО 1	ЮФО	СКФО	ПФО	УФО 1	СФО 1	ДВФО
Период 2003–2009 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	5,5 (0,35)***	-0,18 (0,7)	2 (1,5)	1,7	5,8 (0,5)***	6,2 (0,5)***	5,2 (0,4)***	5,6 (0,3)***
γ 1	0,07 (0,14)	0,3 (0,1)***	0,003 (0,3)	0,01	0,01	-0,4 (0,2)	0,3 (0,2)	0,1 (0,2)
R 2	0,01	0,2	0,001	0,001	0,001	0,1	0,1	0,01
Стат. ошибка	0,8	0,7	0,8	0,8	0,9	0,7	0,8	0,6
Период 2009–2016 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	0,2 (0,13)	5 (0,6)***	5,5 (0,4)***	5,6 (0,5)***	1,2 (0,9)	-0,3 (0,1)**	-0,2 (0,1)*	-0,01
γ 1	0,9 (0,02)***	0,4 (0,4)	0,1 (0,2)	-0,2	0,8 (0,2)***	1 (0,02)***	1 (0,01)***	1 (0,02)***
R 2	0,9	0,1	0,01	0,1	0,8	0,9	0,9	0,9
Стат. ошибка	0,9	0,9	0,8	0,6	0,4	0,1	0,1	0,1
Период 2016–2018 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	0,01 (0,02)	-0,02 (0,02)	0,9 (0,9)	0,02 (0,01)	-0,02 (0,1)	-1,6 (1,4)	-0,001 (0,01)	-0,01 (0,02)
γ 1	0,9 (0,001)***	1 (0,02)***	0,8 (0,2)	0,9 (0,003)***	1 (0,01)***	1,3 (0,3)***	1 (0,01)***	1 (0,04)***
R 2	0,9	0,9	0,8	0,9	0,9	0,8	0,9	0,9
Стат. ошибка	0,02	0,02	0,3	0,01	0,01	0,5	0,01	0,01

Примечание. Рассчитано по данным Федеральной службы государственной статистики. В таблицах 2–6 стандартные ошибки указаны в скобках: *** – уровень значимости ошибки 1 %; ** – уровень значимости ошибки 5 %; * – уровень значимости ошибки 10 %.

Коэффициенты линейного уравнения оценки закона Гибрат по показателю «плотность населения» в городах России в 2003–2018 гг.

Таблица 3

Показатели	ЦФО 1	СЗФО	ЮФО 1	СКФО	ПФО	УФО	СФО	ДВФО
Период 2003–2009 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	7,4 (0,2)***	1,2 (0,7)	6,3 (1,8)***	4,8 (0,9)***	7,3 (0,2)***	7,8 (0,7)***	5,2 (0,5)***	0,8 (0,1)***
γ 1	0,2 (0,1)**	0,1 (0,6)	0,1 (0,3)	0,3 (0,1)**	-0,001 (0,1)	-0,7 (0,4)*	0,3 (0,2)	0,1 (0,01)***
R 2	0,1	0,02	0,01	0,6	0,0001	0,3	0,1	0,5
Стат. ошибка	0,9	0,8	1,2	0,3	0,6	0,8	0,8	0,6

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

Окончание таблицы 3

Показатели	ЦФО	СЗФО	ЮФО	СКФО	ПФО	УФО 1	СФО	ДВФО
Период 2009–2016 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	1,04 (1,7)	5,3 (1,8)**	0,9 (1,2)	-1,4 (1)	0,7 (0,9)	0,2 (0,5)	-0,2 (0,1)*	6,8 (0,8) ***
γ 1	0,9 (0,2)***	0,9 (1,1)	0,2 (1,2)	1,2 (0,14)***	0,9 (0,1)***	0,9 (0,1)***	1 (0,01)***	-0,3 (0,4)
R 2	0,3	0,2	0,1	0,9	0,8	0,7	0,9	0,03
Стат. ошибка	1,1	1,7	0,8	0,2	0,3	0,6	0,07	1,13
Период 2016–2018 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	-0,001 (0,001)	0,001 (0,001)	0,01 (0,001)	3,3 (2)	0,002 (0,001)	0,001 (0,001)	0,001 (0,02)	0,09 (0,0901)
γ 1	1 (1,1)***	1 (0,1)***	1 (1,2)***	-0,2 (0,3)	1 (0,1)***	1 (0,3)***	1 (0,1)***	1 (0,1)***
R 2	0,9	0,9	0,9	0,2	0,9	0,9	0,9	0,9
Стат. ошибка	0,001	0,01	0,9	0,8	0,02	0,4	0,01	0,2

Таблица 4

Коэффициенты линейного уравнения оценки закона Гибрат по показателю среднегодовой численности работников предприятий в городах России в 2003–2018 гг.

Показатели	ЦФО	СЗФО	ЮФО	СКФО	ПФО 1	УФО 1	СФО	ДВФО
Период 2003–2009 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	4,5 (0,4)	0,2 (0,7)	-0,3 (0,2)	3,4 (0,9)***	4,6 (0,5)***	5,2 (0,5)***	3,8 (0,5)***	2 (0,9)*
γ 1	-0,1 (0,2)	0,3 (0,1)**	1 (0,1)***	0,1 (0,5)	0,01 (0,2)	-0,4 (0,3)	0,4 (0,2)	-0,1 (0,2)
R 2	0,01	0,1	0,9	0,01	0,001	0,1	0,1	0,01
Стат. ошибка	1,04	0,7	0,1	0,9	0,8	0,8	0,7	0,7
Период 2009–2016 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	0,2 (0,2)	3,6 (0,6)***	-0,2 (0,1)	0,4 (0,4)	0,2 (0,3)	-0,4 (0,1)***	-0,3 (0,1)*	4,2 (0,3)***
γ 1	0,9 (0,04)***	0,6 (0,5)	1 (0,02)***	0,9 (0,1)***	0,9 (0,1)***	1 (0,02)***	1 (0,02)***	-0,04 (0,2)
R 2	0,9	0,2	0,9	0,9	0,9	0,9	0,9	0,001
Стат. ошибка	0,2	1,12	0,1	0,2	0,3	0,1	0,1	0,7
Период 2016–2018 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	1,11 (0,5)**	-0,05 (0,02)***	2,1 (0,8)**	-0,2 (0,1)	0,2 (0,3)	0,01 (0,04)	0,001 (0,02)	-0,01 (0,06)
γ 1	0,9 (0,01)***	1 (0,02)***	0,01 (0,2)	1 (0,03)	0,9 (0,07)***	0,9 (0,01)***	0,9 (0,004)***	1 (0,01)***
R 2	0,9	0,9	0,1	0,9	0,8	0,9	0,9	0,9
Стат. ошибка	0,1	0,01	0,8	0,1	0,3	0,04	0,02	0,02

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

Таблица 5

Коэффициенты линейного уравнения оценки закона Гибрат по показателю среднемесячной заработной платы в городах России в 2003–2018 гг.

Показатели	ЦФО 1	СЗФО	ЮФО 1	СКФО	ПФО 1	УФО		СФО	ДВФО
Период 2003–2009 гг.
Кол-во наблюдений	46	12	21	14	32	16	20		10
β 0	-3,9 (4,5)	0,1 (0,5)	2,4 (1,4)	9,2 (0,2)***	9,7 (0,1)***	9,9 (0,3)***	3,8 (0,5)***		7,2 (7,9)
γ 1	0,8 (0,5)	0,2 (0,1)**	0,8 (0,2)***	0,2 (0,1)	-0,03 (0,03)	0,1 (0,2)	0,4 (0,2)		-0,6 (0,9)
R 2	0,1	0,2	0,1	0,4	0,02	0,01	0,1		0,1
Стат. ошибка	0,9	0,7	0,5	0,2	0,2	0,8	0,8		0,8
Период 2009–2016 гг.
Кол-во наблюдений	46	12	21	14	32	16		20	10
β 0	10 (0,1)***	10 (0,12)***	8,9 (1,1)***	3 (0,7)***	1,8 (0,6)***	7 (1,6)***		-0,3 (0,1)*	10,9 (0,2)***
γ 1	0,1 (0,04)**	-0,04	0,1 (0,1)	0,7 (0,1)***	0,9 (0,1)***	0,4 (0,2)*		1 (0,02)***	-0,1 (0,1)
R 2	0,1	0,01	0,2	0,9	0,8	0,5		0,9	0,1
Стат. ошибка	0,3	0,2	0,2	0,04	0,1	0,3		0,1	0,3
Период 2016–2018 гг.
Кол-во наблюдений	46	12	21	14	32	16		20	10
β 0	-0,1 (0,2)	-0,07 (0,2)	2,2 (1,3)	0,9 (1)	8,9 (2,1)	-0,1 (0,2)		0,4 (0,2)*	0,3 (0,1)**
γ 1	1 (0,01)***	1 (0,02)***	0,01 (0,7)	0,9 (0,1)***	0,1 (0,8)*	1 (0,02)***		0,9 (0,02)***	0,9 (0,1)***
R 2	0,9	0,9	0,1	0,8	0,2	0,9		0,9	0,9
Стат. ошибка	0,03	0,01	0,8	0,1	1,2	0,02		0,02	0,01

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

Таблица 6

Коэффициенты линейного уравнения оценки закона Гибрат по показателю числа предприятий и организаций на территории городов России в 2003–2016 гг.

Показатели	ЦФО	СЗФО	ЮФО 1	СКФО 1	ПФО 1	УФО	СФО	ДВФО
Период 2003–2009 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	1,8 (0,7)**	8,6 (0,8)***	0,3 (1,4)	9,4 (0,6)***	1,9 (1,2)	10 (0,9)***	8,4 (0,9)***	2,7 (0,9)**
γ 1	0,11 (0,1)	0,6 (0,6)	0,9 (0,1)***	-0,4 (0,3)	0,1 (0,1)	-0,6 (0,5)	0,4 (0,4)	-0,1 (0,1)
R 2	0,04	0,1	0,7	0,2	0,01	0,1	0,1	0,1
Стат. ошибка	0,8	1,3	0,7	0,8	0,9	1,2	1,3	0,7
Период 2009–2016 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	8 (0,8)***	0,4	-0,12 (0,5)	1,2 (1,5)	8,9 (0,8)***	0,3 (0,3)	0,2 (0,4)	9,4 (0,5)***
γ 1	0,3 (0,3)	0,9 (0,03)***	1 (0,1)***	0,8 (0,2)***	0,1 (0,3)	0,9 (0,03)***	0,9 (0,04)***	-0,2 (0,2)
R 2	0,03	0,9	0,9	0,7	0,03	0,9	0,9	0,02
Стат. ошибка	1,3	0,2	0,4	0,5	1,2	0,1	0,4	0,9

Примечание. Рассчитано по данным Федеральной службы государственной статистики.

Окончание таблицы 6

Показатели	ЦФО	СЗФО	ЮФО 1	СКФО	ПФО	УФО	СФО	ДВФО
Период 2016–2018 гг.
Кол-во наблюдений	46	12	21	14	32	16	20	10
β 0	2,3 (1)**	-0,04 (0,08)	2,3 (1,1)	-0,1 (0,1)	-0,2 (0,2)	-0,2 (0,1)*	-0,05 (0,1)	-0,04 (0,07)
γ 1	0,8 (0,1)***	0,9 (0,01)***	-0,02 (0,12)	1 (0,01)***	1 (0,03)***	1 (0,01)***	1 (0,01)***	0,9 (0,01)***
R 2	0,7	0,9	0,1	0,9	0,9	0,9	0,9	0,9
Стат. ошибка	0,6	0,1	0,8	0,1	0,2	0,06	0,04	0,02

Заключение

Проведенное исследование позволяет сделать ряд выводов. В городах России наблюдается широкая дифференциация по показателям, коррелирующим с численностью населения (среднегодовая численность работников предприятий, число предприятий и организаций на территории города). Полученный оценочный коэффициент по ряду показателей как подтвердил, так и опроверг действие закона Гибрат в городах России. За период 2009–2016 гг. в Уральском, Сибирском и Дальневосточном федеральных округах, за период 2016–2018 гг. в Северо-Западном, Приволжском, Сибирском и Дальневосточном федеральных округах темп роста городов не зависит от их первоначального размера.

Также закон Гибрат был подтвержден для показателя плотности городского населения в 2009–2016 гг. в Сибирском федеральном округе, в 2016–2018 гг. – для всех федеральных округов, кроме СКФО; для показателя среднегодовой численности работников предприятий – в Южном (2003–2009 гг., 2009–2016 гг.), Уральском (2009–2016 гг.), Сибирском (2009–2016 гг.), Северо-Западном (2016–2018 гг.), Северо-Кавказском (2016–2018 гг.) и Дальневосточном (2016– 2018 гг.) федеральных округах. Для показателя среднемесячной заработной платы – в Сибирском федеральном округе (2009–2016 гг.); в Центральном, Северо-Западном и Уральском федеральных округах (2016–2018 гг.). Для показателя числа предприятий и организаций на территории города в Южном федеральном округе в 2009– 2016 гг.; в Северо-Кавказском, Приволжском, Уральском и Сибирском федеральных округах – в 2016–2018 годах.

Теоретическая значимость проведенного исследования заключается в расширении спектра показателей проверки закона Гибрат в иерар- хии городов в границах федеральных округов России, что может быть использовано для разработки новых методов оценки данного закона.

Список литературы Анализ действия закона Гибрат в городах России

Андреев В. В., Лукиянова В. Ю., 2015. Проверка закона Гибрат для населенных пунктов Чувашской республики // Вестник Чувашского университета. № 1. С. 154–161.
Андреев В. В., Лукиянова В. Ю., Кадышев Е. Н., 2017. Анализ территориального распределения населения в субъектах Приволжского федерального округа с применением закона Ципфа и Гибрат // Прикладная эконометрика. Т. 48. С. 97–121.
Иванова Т. Б., 2008. Инвестиции: доходность, риск, ликвидность, дюрация. Волгоград : Изд-во ФГОУ ВПО «ВАГС». 191 с.
Манаева И. В., 2016. Как растут города РФ: тестирования закона Гибрат // В. И. Вернадский: устойчивое развитие регионов» : сб. материалов Междунар. науч.-практ. конф., г. Тамбов, 07–09 июня 2016 г. Тамбов : Изд-во Тамбов. гос. техн. ун-та. Т. 2. С. 130–134.
Пирогов Н. К., Поповидченко М. Г., 2010. Закон Гибрата в исследовании роста фирмы // Корпоративные финансы. № 1 (13). С. 106–119.
Allen P. M., Sanglier M., 1979. A dynamic model for growth in a central place system // Geographical Analysis. Vol. 11. Р. 256–272.
Carruthers J. I., Mulligan G. F., 2007. Land absorption in U.S. metropolitan areas: estimates and projections from regional adjustment models // Geographical Analysis. Vol. 39. Р. 78–104.
Clark S., Stabler J., 1991. Gibrat’s law and the growth of Canadian cities // Urban Studies. Vol. 28. P. 635–639.
Chesher A., 1979. Testing the law of proportionate effect // Journal of Industrial Economics. Vol. 27. Р. 403–411.
Eaton J., Eckstein Z., 1997. Cities and growth: theory and evidence from France and Japan // Regional Science and Urban Economics. No. 27. P. 443–474.
Eeckhout J., 2004. Gibrat’s law for (all) cities // The American Economic Review. Vol. 94. Р. 1429–1451.
Gabaix X., 1999. Zipf ’s law for cities: an explanation // Quarterly Journal of Economics. Vol. 114. Р. 739–767.
Gibrat R., 1931. Les Inegalites Economiques; Applications: Aux Inegalites des Richesses, a la Concentration des Entreprises, Aux Populations des Villes, Aux Statistiques des Familles, etc., d’une Loi Nouvelles, La Loi de l’Effet Proportionnel. Paris : Librairie du Recueil Sirey. 296 р.
Gonzáles-Val R., Lanaspa L., Sanz-Gracia F., 2013. Gibrat’s law for cities, growth regressions and sample size // Economics Letters. Vol. 118. Р. 367–369.
Lalanne A., Zumpe M., 2015. Gibrat’s law, Zipf’s law and Cointegration. URL: https://mpra.ub.uni-muenchen. de/67992/.
Manaeva I. V., 2019. Evaluation of temporal growth of Russian cities // In novation Management, Entrepreneurship and Sustainability. Proceedings of the 7th International Conference. Prague. P. 481–494.
Partridge M. D., Rickman D. S., Ali K. and Olfert M. R., 2008. Employment growth in the American urban hierarchy: long live distance // The B.E. Journal of Macroeconomics. Vol. 8 (1). Р. 1–38.
Pérez G., Roca V.A., 2013. Ley de Zipf y de Gibrat para Colombia Y Sus regiones: 1835–2005 // Documentos de Trabajo Sobre Economía Regional. Cartagena. Banco de la República. 192 p.
Robson B. T., 1973. Urban Growth: An Approach. London: Methuen and Co. Ltd. 288 р.
Simon H. A., 1955. On a class of skew distribution functions // Biometrika. No. 42. P. 425–440.
Oke B. O., 2018. Testing the Gibrat’s Law: A Dynamic Panel Analysis of Firm Size and Firm Growth Nexus in Nigeria // Nigerian Journal of Management Studies. Vol. 18, No. 2. P. 77–88.

Еще

Статья научная