Анализ дифракции света на микрообъектах с помощью решения интегрального уравнения методом конечных элементов

В [1, 2] для анализа дифракции поля на микрооптике рассмотрен метод интегральных уравнений Фредгольма второго рода. В данной работе двумерная задача дифракции обобщена на случай объектов с неоднородным показателем преломления. Рассматривается случай, когда внутренняя область состоит из подобластей с постоянным показателем преломления.

Здесь n и n ₂ - векторы внешней к областям й 1 и й ₂ нормали к контуру S соответственно.

Для функций v 1 и G ₂ имеет место формула Грина

1. Постановка задачи

y

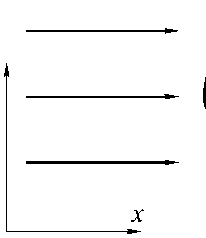
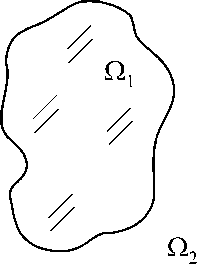
Рис.1. Дифракция плоской волны на прозрачном объекте

Для полей v ₂ V 1 и из й 1 и й ₂ требуется решить дифференциальные уравнения Гельмгольца [2]:

ff ⁽ V 1 ^A G 2 ^- G 2 ^A V 1 ) dxdy = f ^f V 1 ^ G^{2 - G} 2 ^ 1 dl .

й                         S V   д n       д n )

Из уравнений (1) следует

A V 1 = - к 1² ( x , у V 1 , Av 2 = - к 2 V 2 - g 2 .

Для функции Грина справедливо равенство

A G ₂ + к ₂ ² G ₂ = - 5 ( M , M ₀ ) ,

где М - текущая узловая точка, по которой проводится интегрирование, М ₀ - точка наблюдения. Иначе говоря,

5 ( M , M о ) = 5 ( x ', у '; x , у ) .

Подставляя уравнения (4, 5) в уравнение (3), получим f f G2 V- V1 ^Gk 1 dl + JJ (к 12 (x, У)- k2 )■

S V   д n      д n )    "

V 1 G ₂ dxdy - ff V 1 ( x ', У 5 ( x ', у '; x , у ) dx ' dy ' = 0 .       (6)

П 1

( а + к ²( x , у ) V 1 = 0, ( x , у ) ей ] ,

( ^A + к 2 ) / 2 = ^- g 2 ^{,( x ,} У ) ^ей 2 ^,

Использовав свойство 5 - функции, приводим уравнение (6) к виду

где g ₂ - источник во внешней области й ₂, к 1 -волновое поле для среды 1 с неоднородным показателем преломления, к ₂ = ^ ^s ₂ ц ₂ - волновое поле

д V     д G ₂ ^       2        2

УI G 2 , - ^- V 1 -гх²- dll + ]]^{( к} 1 ^{( x ,} у ^{) - к} 2 )■

S V    д n      д n ) й

V 1 G ₂ dxdy =

V 1 , ( x , у ) ей 1 ^{0 , (} x ^, у ^{) ей} 2 .

для среды 2.

Для ТЕ-поляризации граничные условия следуют из непрерывности на границе раздела двух сред тангенциальных составляющих напряженностей электрического и магнитного полей:

V11 s = V 21 s,(x, У) е 5,

Аналогично, применив формулу Грина для функций v ₂ и G ₂ при помощи уравнений (4, 5), получаем:

f ^{f G} 2 ^ ^{VV 1 -} V 2 I GG ¹ ^ d^{l +} ff g 2 ^G 2 ^dxdУ =

S V     ^{д n} 2        ^д n 2 ) й ₂

5 ^ 1

д n

S

^I V 2

^д n 2 S

о , ( x , у ) ей 1

V 2 ^{, ( x ,} У ) ей 2

Сложив уравнения (7) и (8) с учетом граничных условий (2), получим

2 1Д                ^/ V 1 , ⁽ x , y ) ^eQ 1

( k 1 ^- k 2 ^ 1 G 2 dxdy + V 0 = 5    ,   ,       , (9)

n ,                       V 2 , ⁽ x , У h^

где V 0 ( x , У ) = JJ g 2 G 2 dxdy — поле в области П 1 или П 2

Q ₂, созданное источниками с функцией g ₂ ( x , y ) .

Первое из уравнений (9) является интегральным уравнением Фредгольма второго рода относительно V, (x, У) и при Vо * 0 имеет единственное нетривиальное решение.

Далее мы полагаем, что точечный источник находится далеко от области Q 1 , и V ₀ ( x , У ) можно рассматривать как плоскую волну. Рассмотрим случай, когда плоская волна падает вдоль оси х слева направо в выбранной системе координат (рис. 1):

vо=ei2 x.(io)

Функция Грина [3] для двумерных световых полей (цилиндрическая волна) равна функции Ханкеля первого рода нулевого порядка, умноженной на 4 :

G 2 (5 ) = ^H01)(^),(11)

где 5 = k 2 V( x - x ') 2 + ( У — У ') 2 .

По определению

H01)= J0 + ZY0,(12)

где J ₀ – функция Бесселя первого рода нулевого порядка, Y ₀ – функция Неймана нулевого порядка.

где | ^ <  1.4 - 10 ⁸ , 3 < 5 <^ ,

-

J 0 ^{( 5 )} = ^{5 /2} f } cos 0 0

-

Y 0 ^{( 5 )} = ^{5 /2} f } ^{sin 0} 0 ,

I 3 1

f ₀ = 0.79788456 - 0.00000077 1 5 I-

23 f 3 ii

- 0.00552740 1- I - 0.00009512 1- I +

15 J1

+ 0.00137237 1 - I - 0.0007285 1 - I +

15 J1

+ 0.00014476II

15 J где |^ < 1.6 -10 8,

I 3 1

00 = 5 - 0.7853 9816 - 0.041663 971 -3J- i 3 ii

- 0.00003954 I - I + 0.00262573 I - I

15 J1

-

- 0.00054125 I - | - 0.00029333 1 - | +

15 J1

+ 0.00013558 1   | + £ ,

15 J где |^ < 7 • 10-8.

Рассмотрим случай, когда область Q 1 состоит из р частей, в которых k ₁ – постоянная величина

Функции J0 и Y0 аппроксимируются много- членами [4]:

- 3 <  5 <  3,

J 0 ( 5 ) = 1 - 2,2499997 1 ⁵ I

+ 1,2656208 1

-

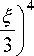
- 0,3163866 1 ⁵ I + 0,0444479 1 ⁵ I

I 3 J                    ( 3 J

-

p

^П 1 = S ⁿ 1 i .

i = 1

Тогда уравнения (9) приобретают следующий вид

/2 /2Vr                    ^/ V 1 , ^{( x} , У ) е ^п1

L(k 1/- k 2)JJV1 G 2 dxdv + V 0 =5    / Ao, i=1          П|                    V2, (x, У)en2

(13) где k 1 i = const внутри подобласти Q 1 i .

10                      12

- 0,0039444 | ⁵ I + 0,0002100 | ⁵ I

13 J 13 J где ^| < 5 • 10-8,

0 <  5 <  3,

Y ) ( 5 ) = -ln [ ⁵ I J ₀ ( 5 ) + 0,36746691 + п I 2 J

+ 0,60559366 f 5		| - 0,74350384 ^	5 Г + 3 J
I	3
+ 0,25300117 1	5	6 J - 0,04261214 1	5" I’ +
	3		3 J
	5	10
+ 0,00427916 1		I - 0,00024846 1	| 5 I 12 I

• 2. Метод расчета

В методе конечных элементов уравнения (9) сводятся к системе алгебраических уравнений. Используя разложение искомого поля по базису интерполирующих функций

N

V ^{( x} , У ) = Z C m V m ⁽ x , У ) ,                    ⁽¹⁴⁾

m = 1

вместо первого из уравнений (9) получаем линейную систему алгебраических уравнений

N

Z C m D mn = V 0 n ,                         ⁽¹⁵⁾

m = 1

где

D mn = V m ⁽ x n , У п ^{) -} JJ^{( k} 12 ^{- k} 22 Vm ⁽ x ', У ' ^{) -}

П 1

G 2 ( X n , У п ; x ', У ' ) dx ' dy ',

V q n = V 0 ⁽ x n , У п ) •

В качестве системы линейных интерполирующих функций можно выбрать функцию вида

1 - x m - x - У т - У

А

А

x m - x А

1 +

V m ⁽ x , У ) =*

У т - У А

1 +

x m - x + У т - У

А

А

1 + x m - x А

, У m - У

1 ■“

(x, у )eQ1 (а1 )

⁽ x , у ) ей ₍ ⁽ А ₂ )

⁽ x , у ) eQ i ^{( а} з ) (17)

⁽ x , у ) €П 1 ^{( а} 4 )

⁽ x , y ⁾ GQ ₁ ^{( а} 5 )

⁽ x , y ⁾ GQ ₁ ^{( а} 6 )

Здесь ( a , c ) - координаты точки, от которой начинается интегрирование, а А ' - шаг внутренней сетки отсчетов, показанной на рис. з.

Так как функция Ханкеля (12) не определена в нуле, то значение интеграла из уравнения (16) можно заменить на интеграл по s - окрестности, где s -сколь угодно малая величина. Можно показать, что при s ^ 0 такой интеграл стремится к нулю.

Матрица системы (14) является полностью заполненной с преобладающей главной диагональю, поэтому для решения системы используется метод Гаусса для комплексных чисел.

где А - шаг сетки отсчетов, показанной на рис. 2.

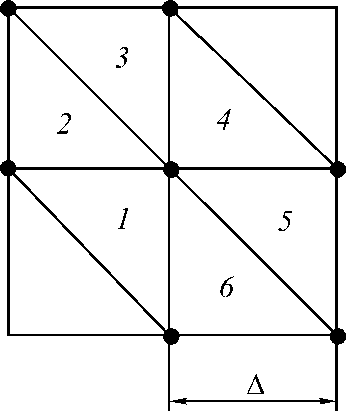
Рис. 2. Фрагмент триангуляции.

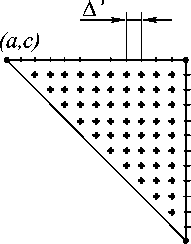
Рис. 3. Разбиение треугольников для численного интегрирования.

Решив систему уравнений (14), получаем комплексные коэффициенты C_m , m = 1,..., N , которые подставляем затем во второе из уравнений (9):

N

V 2 ⁽ x n , У п ) = V 0 ⁽ x n , У п ^{) +} Е C m • m = 1

(a,c)

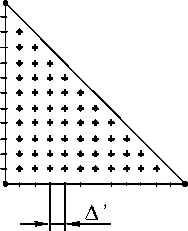
JJ ⁽ k 1^{2 -} k 22 ^ m ^{( X} ', У '^{) G} 2 ⁽ x n , У п ; ^X ', У' ) d^X ' dy '      ⁽²⁰⁾

П ,

Так как подынтегральная функция из уравнения (16) имеет сложный вид, то ее интеграл реализуется численно по каждому из шести треугольников для текущего узла m . При этом для треугольников 2, 4 и 6 он имеет вид:

K K - l

Е Е k 1² ( a + 1 А ', С + Р А ' ) - k 2 ) • l = 0 p = 0

• [ а ( a + 1 А ' ) + в ( c + Р А ' ) + у ] •

• [ J 0 ( X n , У п ; a + 1 А ', c + Р А ' ) +

+ iY 0 ( X n , У п ; a + 1 А ', c + Р А ' )] А ' ² ,               (18)

а для треугольников 1, з и 5 -

K K - l

Е Е^{( k} 1^{2 (} a ^{+ 1 А} ', ^{c -} р ^А ' ^{) - k} 2 ) • l = 0 p = 0

• [ а ( a + 1 А ' ) + в ( с — Р А ' ) + у ] •

•^[ J 0 ( x n , У п ; a ^{+ 1 А} ', ^{С -} Р ^А ' ^{) +}

+ iY ) ( X n , У п ; a + 1 А ', c — Р А ' )] А ' ² .               (19)

3. Численная реализация

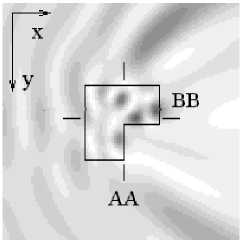
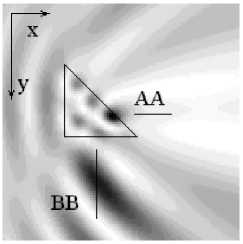
Для сравнения результатов вычислений с гибридным методом, использующимся в работе [2], был выбран квадратный объект с постоянным показателем преломления. Оба метода дали одинаковое решение с расхождением результатов порядка 5%. Ниже приведены примеры дифракции плоской волны с длиной X =1 мкм на однородных объектах типа призмы (рис. 4) и бинарного выступа (рис. 5), а также на прямоугольной области, состоящей из двух квадратов и промежутка между ними (рис. 6). Такую область можно расценивать как объект с участками, где показатель преломления постоянный. Все объекты имеют характерный размер, равный 1 мкм. Показатель преломления всех объектов равен 2. Для среды п = 1. Число отсчетов внешней области -100х100. Число отсчетов внутри объектов можно получить, исходя из расчета 30 отсчетов на 1 мкм. Сечения интенсивности по x и у (рис. 4-6б, в) вычислены в местах, указанных штрихами на рис. 4-6а. Интересно отметить, что не зависимо от формы объекта максимальное значение интенсивности достигается внутри объекта вблизи его контура.

а)

а)

б)

а)

I            Сечение по X

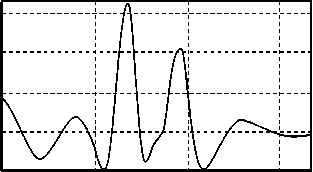
y, мкм в)

I              Сечение по Y

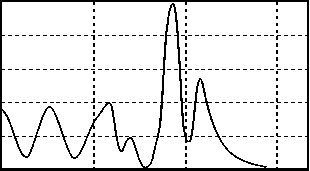
x, мкм

Рис. 4. Дифракция плоской волны на однородном бинарном выступе: а) распределение интенсивности в плоскости XY; б) сечение по Х; в) сечение по Y.

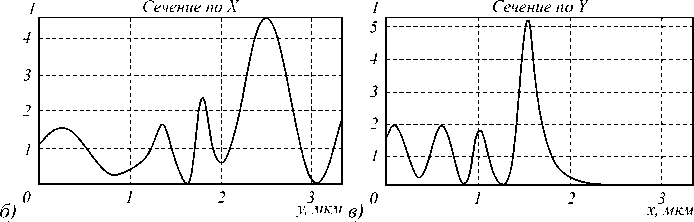
Рис. 5. Дифракция плоской волны на однородной треугольной призме: а) распределение интенсивности в плоскости XY; б) сечение по X; в) сечение по Y.

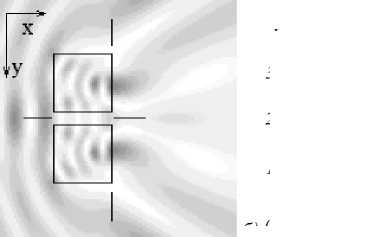
б)

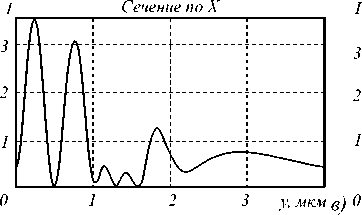
Рис. 6. Дифракция плоской волны на кусочно однородном объекте (два квадрата): а) распределение интенсивности в плоскости XY; б) сечение по Y; в) сечение по Х.

Сечение по X

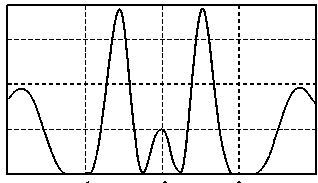
v, .мкл.

Заключение

Разработан метод анализа дифракции света на прозрачных цилиндрических микрообъектах с произвольным контуром и с неоднородным распределением показателя преломления.

Работа поддержана Российским фондом фундаментальных исследований (гранты 99-01-39012, 00-01-00031, 0015-96114)