Анализ динамики поступлений в бюджет от московского рынка наружной рекламы

нятия решений (СППР) [1]. Информационнопоисковые, оперативно-аналитические, а также интеллектуальные СППР обеспечивают, соответственно, возможность поиска необходимых данных, их группировку и обобщение, а также поиск функциональных и логических закономерностей в накопленных данных, построение моделей и правил, которые объясняют найденные закономерности или прогнозируют развитие некоторых процессов.

Подсистема хранения информации в СППР использует современные системы управления базами данных (СУБД) и концепцию хранилищ данных. Предложенная Эдгаром Коддом модель многомерных данных в виде так называемого информационного гиперкуба и сформулированные им правила формирования реляционных СУБД являются фундаментальной основой для проектирования указанной выше структурной компоненты СППР.

В данной работе исследуется многомерная модель данных в виде помесячных поступлений в бюджет г. Москвы от объектов наружной рекламы (ОНР) в период с 2008 по 2011 год.

Подсистема интеллектуального анализа данных использует современные методы и алгоритмы Data Mining. К типичным задачам этого раздела теории искусственного интеллекта относят такие, как формирование описательных и прогнозных моделей. Первые улучшают понимание человеком анализируемых данных с помощью поиска ассоциативных правил и алгоритмов кластеризации, т.е. группировки однородных объектов. Вторые призваны идентифицировать модели данных по набору обучающих пар «вход – выход» и выполнить прогнозирование результатов для новых наборов наблюдений. К такому виду относят задачи классификации объектов по их характеристикам и поиска регрессионных зависимостей.

В данной работе представлена методика анализа, моделирования и прогнозирования нестационарных временных рядов (НВР) помесячных поступлений в московский бюджет от ОНР по типам рекламы и городу в целом. Важной особенностью предлагаемой методики является ее адекватность экспериментальным измерениям в условиях малого объема выборки. Этот результат достигается за счет применения интеллектуальных моделей локально взвешенной полиномиальной регрессии и робастного оценивания основных статистик НВР.

Современная методология адекватного прогнозирования НВР основана на рациональном сочетании экспертных моделей данных, а также методов адаптивного анализа и моделирования временных рядов [2]. Экспертный подход к анализу исходной информации позволяет учесть ее неопределенность. Плодотворным в этом смысле является, на наш взгляд, применение систем, основанных на обработке знаний экспертов с помощью алгоритмов нечеткого логического вывода.

Важной особенностью адаптивного направления анализа НВР является учет ожиданий участников инвестиционного процесса, а также возможности возникновения и влияния случайных факторов. Исследование различных сценариев развития событий позволяет естественным образом учесть указанные выше особенности прогнозирования НВР. Существенное значение в этом смысле приобретает управление результатами прогноза с помощью параметров эконометрических моделей НВР. В данной работе представлен анализ различных сценариев прогноза поступлений в бюджет г. Москвы от ОНР на основе гибких адаптивных моделей динамики временных рядов.

Модель многомерных данных

Трехмерная модель исходных данных представляет собой информационный «куб» [1] со следующими измерениями:

• 1)    «время» в виде последовательности месяцев n = 1,2,..., N ( N = 48 ) в период с 2008 по 2011 год включительно;

• 2)    «округ» в виде упорядоченной последовательности административных округов г. Москвы m = 1,2,..., M ( M = 11 ) , представленных в таблице 1 по состоянию на 2011 год;

• 3)    «тип ОНР» в виде упорядоченной последовательности типов наружной рекламы k = 1,2,..., K ( K = 30 ) , представленных в таблице 2.

Меры, расположенные на пересечении осей измерений, представляют собой отчисления в московский бюджет от ОНР в миллионах рублей. СУБД поддерживает стандартные операции среза, вращения, консолидации и детализации над многомерной моделью данных [1].

Таблица 1

Административные округа

n 2	Наименование
1	Общегородской заказ (ОГЗ)
2	Восточный административный округ (ВАО)
3	Западный административный округ (ЗАО)
4	Зеленоградский административный округ (ЗелАО)
5	Северный административный округ (САО)
6	Северо-восточный административный округ (СВАО)
7	Северо-западный административный округ (СЗАО)
8	Центральный административный округ (ЦАО)
9	Южный административный округ (ЮАО)
10	Юго-восточный административный округ (ЮВАО)
11	Юго-западный административный округ (ЮЗАО)

ВЕСТНИК 2013 № 4

В качестве примеров на рис. 1 и 2 представлены графики НВР отчислений в городской бюджет по месяцам. Рис. 1 иллюстрирует данные, полученные в результате консолидации по округам и среза для ОНР «Щит отдельно стоящий». Рис. 2 демонстрирует динамику поступлений, консолидированных как по округам, так и по типам рекламы.

ВЕСТНИК 2013 № 4

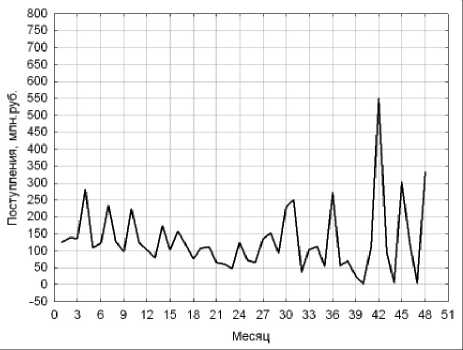
Рис. 1. Консолидированные по округам поступления от ОНР «Щит отдельно стоящий»

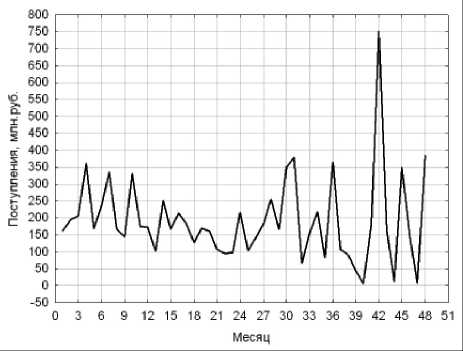
Рис. 2. Консолидированные поступления в бюджет от ОНР

Таблица 2

Типы наружной рекламы

n 3	Наименование
1	Витраж
2	Выносная щитовая конструкция (штендер)
3	Информационная конструкция предприятия и организации по обслуживанию населения на здании
4	Кронштейн на здании (площадью одной стороны более 1 кв. м и высотой более 1,5 м)
5	Кронштейн на здании (площадью одной стороны менее 1 кв. м и высотой менее 1,5 м)
6	Кронштейн на несветовой опоре
7	Кронштейн на световой опоре
8	Крышная установка
9	Маркиза

В процессе анализа данных и поиска решений часто возникает необходимость в построении зависимостей между различными показателями. Число таких показателей может варьироваться в широких пределах. Таблицы реляционных баз данных не удовлетворяют требованиям объединения, просмотра и анализа информации с точки зрения множественности измерений. Оперативный многомерный анализ выполняют OLAP (On-Line Analytical Processing) – системы, предложенные Эдгаром Коддом в 1993 году. Основное назначение OLAP-технологии состоит в поддержке произвольных запросов аналитиков. Цель OLAP-анализа – проверка возникающих гипотез. Пример оперативного анализа структуры поступлений в московский бюджет от ОНР иллюстрирует рис. 3.

Визуальный анализ диаграмм рассеяния помесячных поступлений, сформированный OLAP-системой для 30-ти типов рекламы, позволяет аналитику ранжировать рекламные объекты по уровню их доходности. Вполне очевидной является следующая последовательность шести ОНР, упорядоченных по убыванию значимых суммарных поступлений за период с 2008 по 2011 год:

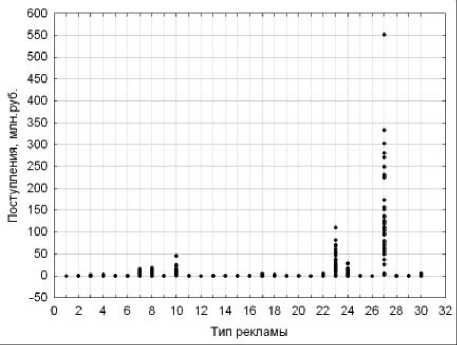
Рис. 3. Диаграммы рассеяния поступлений в бюджет от ОНР

• 1)    щит отдельно стоящий (27)   –

  6301,21481116 млн руб.;

• 2)    транспарант-перетяжка      (23)      –

  1404,36650349 млн руб.;

• 3)    настенное панно площадью более 2 кв. м (10) – 421,79276631 млн руб.;

• 4)    крышная установка (8) – 321,92105990 млн руб.;

• 5)    кронштейн на световой опоре (7) – 228,86775148 млн руб;

• 6)    тумба отдельно стоящая (24)   –

  177,54042206 млн руб.

Графики временных рядов поступлений в московский бюджет от этих типов рекламы представлены в логарифмическом масштабе на рис. 4. Поступления для первых трех типов (с номерами 27, 23 и 10 из таблицы 2) измерены по левой вертикальной шкале. Остальные – по правой шкале.

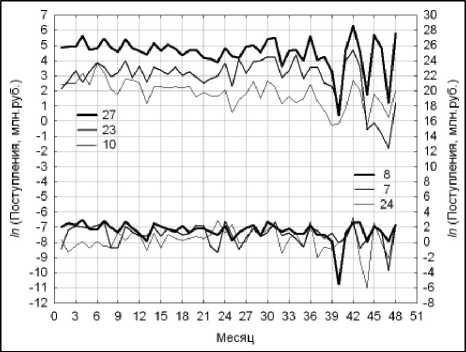
Рис. 4. Помесячные поступления от ОНР со значимой доходностью

Главная задача аналитика – это формирование гипотез на основе своих знаний и опыта. Гигабайты и терабайты накопленных данных содержат значительный объем «скрытых» знаний, которые человек не в состоянии исследовать самостоятельно. Существует высокая вероятность пропустить значимые гипотезы.

Методологию обнаружения «скрытых» знаний в больших объемах накопленной информации называют добычей данных (Data Mining). Data Mining – это алгоритмическое обнаружение в исходных данных «скрытых» знаний, которые ранее не были известны, нетривиальны, практически полезны и доступны для интерпретации человеком.

Рекуррентные статистики временного ряда

Рассмотрим одну из задач, решаемых с помощью подсистемы интеллектуального анализа данных СППР, а именно: задачу анализа и моделирования НВР x ( n ) , n = 1,2, . , N в виде консолидированных помесячных поступлений в бюджет г. Москвы от ОНР. При формировании эконометрической модели указанного временного ряда необходимо учитывать относительно малый объем выборки, содержащей N = 48 отсчетов, и наличие аномальных значений (см. рис. 2). Надежной методической основой для решения указанной выше задачи является применение рекуррентного сглаживания НВР [3] с помощью процедур локально взвешенной полиномиальной регрессии [4; 5]. В частности, для оценивания основных статистик НВР удобными, на наш взгляд, являются модели:

• –    ядерной робастной регрессии (Robust Locally Weighted Regression and Smoothing Scatterplots) [4];

• – наименьших квадратов, взвешенных «расстоянием» (Distance Weighted Least Squares – DWLS) [5];

  – экспоненциально взвешенной робастной регрессии (Exponential Weighted Regression – EWR) [6];

  – комбинация моделей DWLS и EWR (DEWR) [3].

В алгоритме рекуррентного сглаживания параметрические модели начального ( i = 1 ) и остаточных ( i = 2,3,... ) трендов у, ( n - т ) для отсчета относительного времени т аппроксимируют локально постоянной y , ( n - т ) = с 0 ' ) ( т ) , линейной у , ( n - т ) = с ⁽ ₀ ' ) ( т ) + т с 1 ' ) ( т ) или квадратичной у , ( n - т ) = с 0 ' ) ( т ) + т с 1 ' ) ( т ) + т ² с 2 ) ( т ) зависимостью. Относительное время τ будем вычислять по схеме прогнозирования «вперед»,

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

т.е. τ = n – t . Здесь t – временн о й отсчет в пределах интервала сглаживания n - s i N + 1 <  t <  n , для которого оценивают значение начального или остаточного тренда, а 0,2 <  s i <  0,8 - доля наблюдений, по которым выполняют сглаживание [4] на i -ой итерации удаления трендов [3]. В этом случае 0 <  т <  s i N - 1 и начало отсчета т = 0 соответствуют правой границе t = n интервала сглаживания. Альтернативный выбор т = n - t - ( s i N - 1 ) Д отвечает «центрированной» оценке тренда, поскольку в этом случае |т |< ( s i N - 1 ) /2 и начало отсчета т = 0 соответствуют середине t = n - ( s i N - 1 ) Д интервала сглаживания.

В дальнейшем для определенности будем рассматривать квадратичную аппроксимацию, которая, в большинстве случаев, позволяет хорошо оценивать тренды, а также их темп изменения и кривизну, в особенности в окрестностях локальных экстремумов исходного и остаточного временных рядов.

Вектор Ci (т) = { c(0i) (т),c 1 ) (т),c2i) (т)} оптимальных коэффициентов полинома на i-ой итерации сглаживания выбирают из условия ми- нимума

^Ci ( ^т )| opt = Arg ^min “ Z w 1 i ) ( ^{т -} j ) ^w 2 i ) ^ ^с , (^т ) [ j = 0

^{ ri ( n -j)} ri2 ( n -j)'                    (1)

взвешенного квадрата текущего остатка [4; 5]

r ( ⁿ ) = Г - 1 ( ⁿ )^- У, ( ⁿ ) , i = 1, 2, — .

Здесь J, = siN; w 1 i)(т) и w(21){ ri (n - т)} -локальный и робастный веса остатка [7]. Исходный временной ряд r0 ( n ) = x ( n) инициализирует алгоритм рекуррентного оценивания. Рациональными критериями завершения итераций являются сходимость средней энергии текущих трендов к нулевому уровню ei =

N

Z ^w 2 i ) { r ( ⁿ ) } y 2 ( ⁿ )

n = 1

N

N Z w (2 i){ ri ( n )}

n = 1

< £ 1 , i = 1, 2, ...

или незначительное изменение средней энергии остаточных трендов за одну итерацию

I ei+1 - ei |< £ 2, i = 2, 3, —, где £1 > 0 и £ 2 > 0 - выбранные пользовате- лем достаточно малые уровни значимости критериев. Критерий окончания итераций i < Imax страхует неудачный выбор допусков. Финаль- ные модели остаточного ряда и тренда рассчитывают по формулам

r ( n ) = г, ( n ) , y ( n ) = x ( n ) - r ( n ) , где I <  I _max - номер заключительной итерации.

Локальный вес w 1 i ) ( т - j ) текущего остатка r i ( n - j ) обратно пропорционален временному интервалу между отсчетами т и j относительного времени. Поэтому значимый вклад в оценку параметров C i ( т ) полиномиальной регрессии y i ( n - т ) вносят лишь те наблюдения r i - 1 ( n - j ) , для которых отсчеты j близки к моменту времени т по критерию веса w ^{( i} ) ( т - j ) .

С этой точки зрения масштаб s i весовой функции удобно интерпретировать как параметр сглаживания данных. Вычислительные эксперименты показали, что для обеспечения быстрой сходимости процедуры рекуррентного оценива- ния в соответствии с указанными выше критериями текущий масштаб si рационально увели- чивать по мере увеличения номера итерации, т.е.

si-1 + As , si-1 < ^max max , si-1      max

I .    (2)

Локальный вес в модели Lowess w(i)(т) = = Ker{(т) / si}! si определяется выбором положительной четной функции ядра Ker(и), заданной на стандартном интервале [–1; 1] и интегрируемой с единицей J Ker (и) du = 1. Модели наиболее популярных ядер представлены в монографии [8, с. 140]. В частности, Клевеланд (Cleveland) рекомендует применять трижды кубическое ядро [4]

Ker ( и ) = <

70 ( 1 -| и |³) 3^81, | и | < 1

, | и | >  1.

Начальный масштаб ядра s ₁ выбирают с помощью процедуры скользящей проверки [8].

Локальный вес в модели DWLS удобно, на наш взгляд, вычислять с помощью формулы w 1 ) ( т ) = s i N Д v ( s i ) т ² + s i N } , где v ( s ) - скорость убывания веса в виде полинома, степень и коэффициенты которого выбирают эмпирически. В наших вычислительных экспериментах выбран полином пятой степени следующего вида

v ( s ) = 3,9301 - 33,9621 s + 122,1792 s ² -

- 221,3187 s ³ + 198,7453 s ⁴ - 70,3125 s ⁵.

График этого полинома представлен на рис. 5. В модели DWLS, как известно, отсутствует механизм робастного взвешивания остатков. Поэтому все веса w ⁽ ₂ i ) { r i ( n - j ) } , i = 1,2, _ , I полагают равными единице.

В алгоритмах, реализующих модели Lowess и DEWR, предусмотрен дополнительный (внут-

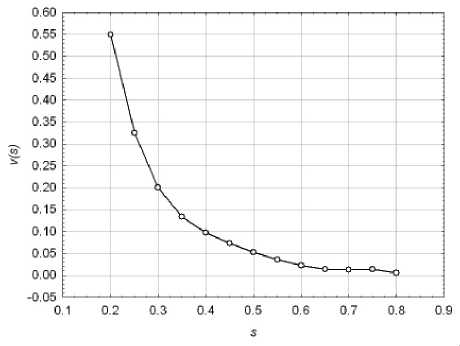
Рис. 5. Зависимость скорости убывания локального веса от параметра сглаживания модели DWLS

ренний) цикл робастного оценивания. Для фиксированной итерации i внешнего цикла локального взвешивания вес остатков w2) {ri ( n - j)} на первой итерации робастного сглаживания по- лагают равным единице, поскольку отсутствует информация об остатке ri ( n - j). На последующих итерациях вес обратно пропорционален остатку. Такая зависимость позволяет исключить влияние аномальных значений временного ряда на параметры C, (т) полиномиальной регрессии y , (n - т) [6, 7]. Важно также отметить, что на второй и последующих итерациях робастного оценивания реализуют процедуру скользящего контроля, т.е. из суммы квадратов остатков в выражении (1) для целевой функции исключают отсчет j = т . Сглаживание продолжают до тех пор, пока робастные веса не стабилизируются. На практике процесс сходимости ограничивают двумя-тремя итерациями.

В модели Lowess Клевеланд рекомендует применять робастное взвешивание остатков, предложенное Хубером (Huber). Весовая функция Хубера имеет вид

Г2 (n - j), |r( n - j )|> R, 1 R^ n - j )|-R,2, |r( n - j )|> R, , w 2){ r( n - j )} = *

где R , = 1,345 RMS, ; RMS , - робастная мера масштаба остаточного НВР на - ой итерации локально взвешенного сглаживания. В качестве такой меры рационально применять абсолютное медианное отклонение [9]. Различные варианты выбора робастных весовых функций представлены в работах [6; 7].

В комбинированной модели DEWR оптимальные параметры полиномиальной регрессии выбирают из условия минимума функции потерь [3]

Г

C , ( ^т )| opt = Arg imin i ^a - ^{N1+ X )} ( ^т ) E w ^{( , )} ^

Ci(т) [

^(т-j)w21){r,(n-j)} -.

Здесь w 2 ) { г ( n - j ) } = exp { - 2 r , ²( n - j )/ j ( 2 a , ² ( n - j ) ) } - робастная весовая функция Л.Д. Мешалкина [6]; a , ( n - j ) - экспоненциально взвешенная (ЭВ) оценка дисперсии остаточного НВР r , ( n - j ) на текущем временном интервале сглаживания 0 <  j <  s , N - 1; X >  0 -параметр устойчивости ЭВ-регрессии к аномальным значениям данных.

Решение задач квадратичной оптимизации (1) и (3) приводит к системам линейных и нелинейных уравнений, соответственно [3]. Канонический вид этих систем позволяет решать их методом последовательных приближений. В качестве начальных оценок для тренда и дисперсии исходного и остаточных НВР выбирают стандартные оценки, полученные с помощью процедуры простой скользящей средней

1Ji y,( n )=   E r-i(n - j),

J , j = 0

1J aA n )= E rA n- j), ^1,2,-, I.

J j = 0

Важным этапом формирования оценок основных статистик НВР является обоснование выбора параметров локально взвешенной полиномиальной регрессии.

ВЕСТНИК 2013 № 4

Выбор параметров локально взвешенной полиномиальной регрессии

Как упоминалось выше, начальное значение параметра сглаживания s 1 обычно выбирают с помощью функции скользящей проверки (CrossValidation). Альтернативный критерий оптимальности параметра s1 , реализующий идею регуляризации модели локально взвешенной полиномиальной регрессии, основан на введении штрафа за ее сложность. В частности, рациональной, на наш взгляд, является целевая функция si| opt = Arg min (DRF);

DRF = DR + ^ DF ,                   (4)

где

NN

^DR =^E ^{r 2 ( n} ) ; ^DF =t^E(^{a 2} y ^{( n} ) ) ;

N n = 1                 N ² n = 3

ВЕСТНИК 2013 № 4

γ > 0 – вес штрафа за кривизну финального тренда

A2 y ( n ) = y ( n)- 2 y ( n -1) + y ( n - 2), n = 3,4,..., N.

Уместно отметить, что целевая функция (4) аналогична критерию оптимальности цифрового фильтра Ходрика – Прескотта [3]. Кроме того, компоненту DF в выражении (4) удобно интерпретировать как дисперсию ошибки прогноза в среднем. Действительно, вторую разность A ² y ( n ) финального тренда можно представить в виде ошибки

А ² y ( n ) = £ ( n ) = y ( n ) — y 1 ( n — 1 ) наивного локально линейного прогноза

У 1 ( ^{n -} 1 ) = у ( ^{n -} 1 ) ^{+ 8} 1 ( ^{n -} 1 ) тренда на один шаг времени. Здесь 8 1 ( n - 1 ) = = y ( n - 1 ) - y ( n - 2 ) - текущий темп измене -ния тренда. Иными словами, смысл критерия (4) состоит в выборе оптимального значения параметра s ₁ модели локально взвешенной полиномиальной регрессии, обеспечивающего разумный компромисс между дисперсией DR ошибки r ( n ) аппроксимации данных и дисперсией DF ошибки 8 ( n ) локально линейного прогноза в среднем.

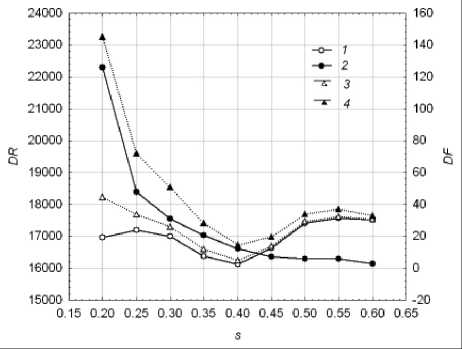
Рис. 6. Зависимость целевой функции от параметра сглаживания модели Lowess: 1 – дисперсия ошибки аппроксимации данных;

2 – дисперсия ошибки локально линейного прогноза тренда; 3 – целевая функция для γ = 10;

4 – целевая функция для γ = 50

Рис. 6 и 7 иллюстрируют зависимости целевой функции (4) от начального значения s ₁ параметра сглаживания в рекуррентной процедуре оценки тренда консолидированных поступлений в московский бюджет от ОНР (см. рис. 2) для моделей Lowess и DWLS. Целевая функция, изме-

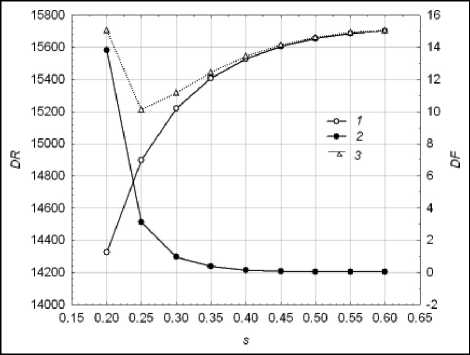
Рис. 7. Зависимость целевой функции от параметра сглаживания модели DWLS: 1 – дисперсия ошибки аппроксимации данных;

2 – дисперсия ошибки локально линейного прогноза тренда; 3 – целевая функция для γ = 100

ренная в масштабе левой вертикальной шкалы, соответствует различным значениям штрафа γ за ошибку прогноза.

В модели Lowess выполнялись три итерации робастного взвешивания. Параметры правила (2) управления локальным взвешиванием для указанных моделей сглаживания сведены в таблицы 3 и 4. Четвертый и пятый столбцы таблиц содержат значения средней энергии начального и финального остаточных трендов.

На рис. 8 представлены оценки трендов консолидированных поступлений в бюджет г. Москвы от ОНР, полученные с помощью моделей Lowess и DWLS с параметрами s 1 = 0,4 и s 1 = 0,25, соответственно.

Таблица 3

Параметры управления рекуррентным сглаживанием в модели Lowess для оценки тренда

s 1	S max	I	e 1	e i
0,2	0,6	10	26,184581	0,038549
0,25	0,65	13	25,781354	0,062346
0,3	0,7	15	25,887734	0,079519
0,35	0,75	10	25,694735	0,086252
0,4	0,8	17	25,185234	0,111986
0,425	0,8	11	25,066667	0,125209
0,45	0,8	14	24,984593	0,123597
0,5	0,8	14	24,749617	0,131539
0,55	0,8	14	24,716589	0,144613
0,6	0,8	10	24,722549	0,161205

Таблица 4

Параметры управления рекуррентным сглаживанием в модели DWLS для оценки тренда

s 1	S max	I	e 1	eI
0,2	0,6	20	27,857751	0,004018
0,25	0,65	20	27,867429	0,004717
0,3	0,7	20	27,881724	0,005683
0,35	0,75	20	27,890537	0,006215
0,4	0,8	20	27,896649	0,004679
0,45	0,8	20	27,902536	0,003619
0,5	0,8	20	27,909339	0,002367
0,55	0,8	20	27,917260	0,001814
0,6	0,8	20	27,924725	0,002382

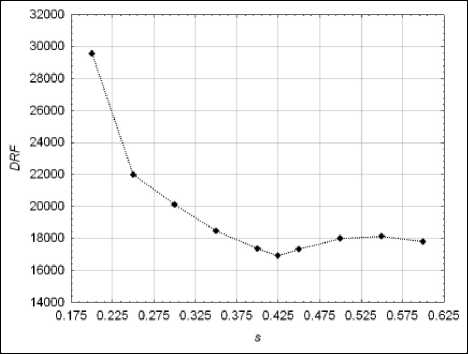
Рис. 9. Зависимость целевой функции от параметра сглаживания модели Lowess для γ = 100

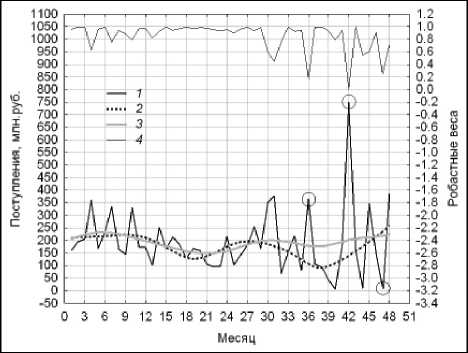
Рис. 8. Финальные тренды для различных моделей сглаживания:

1 – консолидированные поступления в бюджет от ОНР ;

2 – модель Lowess; 3 – модель DWLS;

4 – робастные веса Хубера

Очевидно, что экспертные ожидания тенденции развития московского рынка наружной рекламы плохо согласуются с результатами, формируемыми моделью Lowess. Такой результат обусловлен весьма малыми величинами робастных весов Хубера, измеренных на рис. 8 по правой вертикальной шкале, для 36-го, 42-го и 47-го отсчетов НВР. Иными словами, вес штрафа за ошибку прогноза в среднем 10 ≤ γ ≤ 50 дает несколько заниженное оптимальное значение s ₁ = 0,4 параметра сглаживания для модели Lowess.

Достаточно хорошо согласованные оценки финального тренда обеспечивает выбор веса штрафа γ = 100 для модели Lowess и оптимальное значение s ₁ = 0, 425 . Зависимость целевой функции (4) от параметра сглаживания s ₁ для этого случая демонстрирует рис. 9.

Оценки трендов, соответствующие указанному выше выбору параметров моделей сглаживания Lowess и DWLS, представлены на рис. 10.

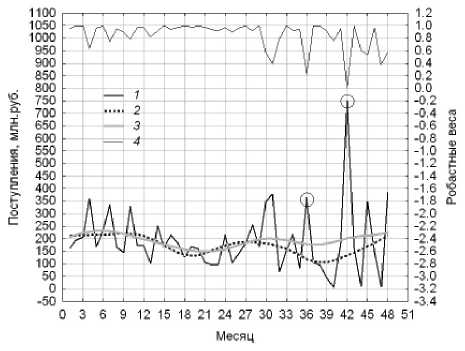
Рис. 10. Оптимальные оценки тренда для различных моделей сглаживания:

1 – консолидированные поступления в бюджет от ОНР;

2 – модель Lowess; 3 – модель DWLS;

4 – робастные веса Хубера

ВЕСТНИК 2013 № 4

Рекуррентные робастные оценки тренда

Наряду с моделью Lowess на практике широкое распространение получила модель EWR – экспоненциально взвешенной робастной регрессии Л.Д. Мешалкина. Ее преимущества обусловлены, прежде всего, гибким механизмом управления робастным взвешиванием и высоким прогнозным потенциалом [6].

Анализ зависимости целевой функции (4) от параметра λ устойчивости статистик к аномальным значениям НВР показывает (рис. 11), что в широком диапазоне величин 10 ≤ γ ≤ 1600

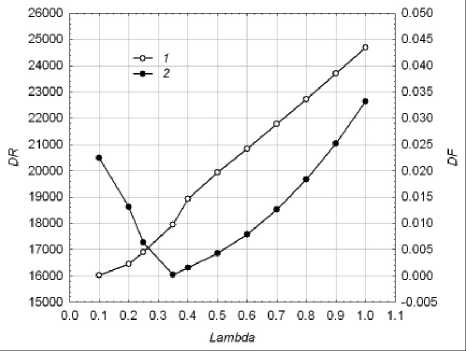
Рис. 11. Зависимость целевой функции от параметра λ устойчивости модели EWR: 1 – дисперсия ошибки аппроксимации данных;

2 – дисперсия ошибки локально линейного прогноза тренда

ВЕСТНИК 2013 № 4

штраф DRF ( λ ) практически не отличается от значений дисперсии DR ( 2 ) остаточного ряда. Поэтому для временного ряда консолидированных поступлений в московский бюджет от ОНР предпочтительным является величина 2 = 0,1.

Процесс стабилизации робастных весов w 2 i ) { r i ( n ) } , 1 - n - N по критерию расстояния в N -мерном пространстве Евклида для этого случая иллюстрирует рис. 12.

Высокий потенциал модели экспоненциально взвешенной робастной регрессии для прогнозирования тренда НВР демонстрирует рис. 13. В зависимости от выбора значения 2 темп изменения тренда за один шаг времени и робастные веса, измеренные в масштабе правой вертикальной шкалы, варьируются в широких диапазонах для правой границы сегмента данных.

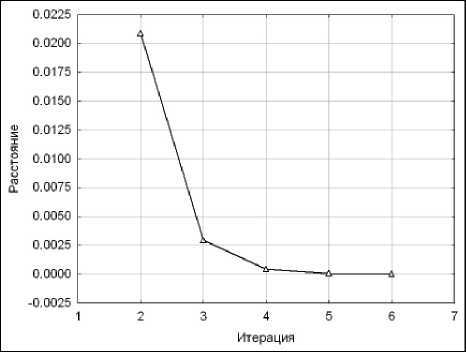
Рис. 12. Сходимость процедуры робастного взвешивания модели EWR для λ = 0,1

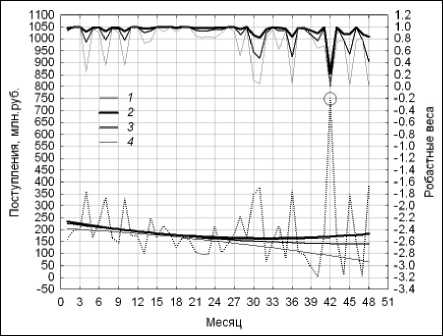
Рис. 13. Оценки тренда для модели сглаживания EWR: 1 – консолидированные поступления в бюджет от ОНР;

2 – тренд для λ = 0,1; 3 – тренд для λ = 0,25;

4 – тренд для λ = 0,5

Иными словами, модель EWR обеспечивает возможность управления результатами прогноза в среднем с помощью адаптации параметра 2 по мере поступления новых данных. Очевидно, что комбинация локального и робастного взвешивания, реализованная в модели DEWR [3], и соответственно адаптация по параметрам s 1 и 2 может усиливать указанное выше свойство.

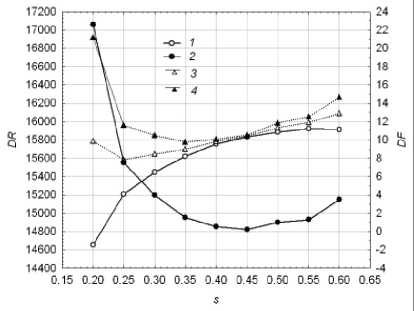
а) λ = 0,1

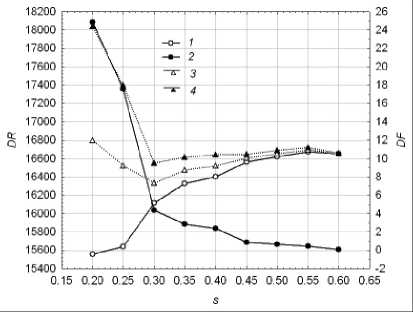
б) λ = 0,25

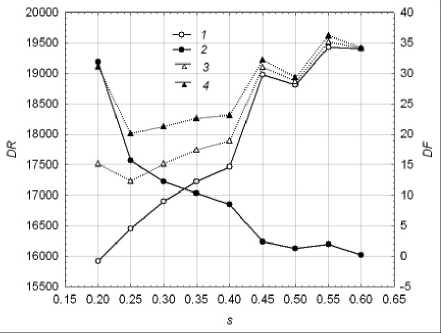
в) λ = 0,5

Рис. 14. Зависимость целевой функции от параметра сглаживания модели DEWR: 1 – дисперсия ошибки аппроксимации данных; 2 – дисперсия ошибки локально линейного прогноза тренда; 3 – целевая функция для γ = 50;

4 – целевая функция для γ = 100

от выбора параметра устойчивости статистик к аномальным значениям в диапазоне значений 0,1 < X <  0,5.

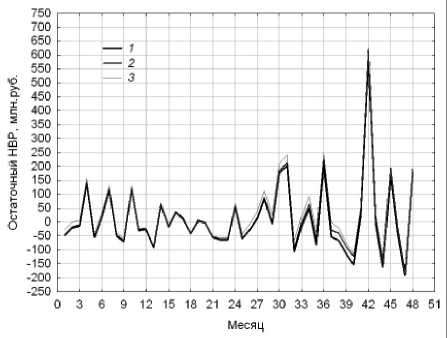
Рис. 16. Оценки остаточного НВР для модели DEWR с параметром сглаживания s ₁ = 0,35:

1 – λ = 0,1; 2 – λ = 0,25; 3 – λ = 0,5

Рациональный выбор параметров s ₁ и λ комбинированной модели сглаживания по критерию (4) обосновывает зависимости, представленные на рис. 14. Соответствующие оценки тренда консолидированных поступлений в бюджет г. Москвы от ОНР иллюстрирует рис. 15.

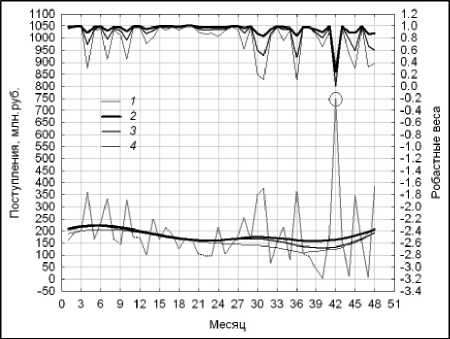
Рис. 15. Оценки тренда для модели DEWR с параметром сглаживания s ₁ = 0,35:

1 – консолидированные поступления в бюджет от ОНР ;

2 – тренд для λ = 0,1; 3 – тренд для λ = 0,25;

4 – тренд для λ = 0,5

Наш выбор квазиоптимальных параметров модели DEWR состоит в следующем: s 1 = 0,35 и X = 0,1. В этом случае результаты моделирования хорошо согласуются с экспертными ожиданиями темпа изменения тренда для московского рынка наружной рекламы. Более того, оценки остаточного НВР r ( n ), 1 ≤ n ≤ N (рис. 16) для его правого сегмента практически не зависят

Рекуррентные робастные оценки волатильности

Масштаб данных рационально оценивать с помощью алгоритма рекуррентного сглаживания квадрата остаточного НВР r ( n ) [3]. В этой процедуре начальную ( i = 1) и остаточные ( i = 2,3,. . ) меры волатильности v 2 ( n ) удобно аппроксимировать следующими локальными регрессионными моделями: v 2 ( n - т ) = g ⁽₀¹ ) ( т ) — постоянной; v ² ( n - т ) = g ⁽ ₀ ¹ ) ( т ) + т g 1 ¹ ) ( т ) - линейной; v ² ( n - т ) = g 0* ) ( т ) + т д 1 ¹ ) ( т ) + т ² g 2 ¹ ) ( т ) - квадратичной. Здесь 0 <  т <  J, - 1 - относительное время, вычисленное по схеме прогнозирования «вперед». В дальнейшем для определенности будем рассматривать квадратичную аппроксимацию.

Векгор G 1 (^т ) = { g 0 ¹ ) ^т ) , g 1 ¹ ' ( г ) , g 2 ¹ ) ( ^т ) } оптимальных коэффициентов полинома на i -ой итерации сглаживания выбирают из условия минимума

Г J - 1

G 1 ( ^т ) I opt = Arg Im in 1 £ w ⁽ 1 ¹ ) ( ^т - j ) w ⁽ 2 ¹ ) ^ ⁵ 1 ^(т ) [ j = 0

^ { ^R1 ² ( n - j ) } ^{R 2} ( n - j ) ' взвешенного квадрата остатка

R 1 ( ⁿ ) = u 1 - 1 ( ⁿ )^- v 1 2 ( ⁿ ) , i = 1, ², - .

Здесь w 11 ^{1 )} ( т ) и w ( 2¹ ) { R ² ( n - т ) } - локальный и робастный веса. Квадрат остаточного НВР u ₀( n ) = r ²( n ) инициализирует алгоритм рекуррентного оценивания. На каждой итерации локального сглаживания выполняют нормировку u₁ ( n ) = u ^1 ( n )/ v ² ( n ) , что обеспечивает схо-

ВЕСТНИК 2013 № 4

димость текущей меры волатильности v² ( n ) , 1 ≤ n ≤ N к единичному уровню в метрике Евклида. Соответственно стандартные критерии завершения итераций имеют вид:

E i =

N ₂

X w ⁽ 2 ) { R i ( n ) }{ v ( n ) - 1 } n = 1

N

NЕ w2°{ Ri2 ( n)}

n = 1

< 5 1 ,

i = 1, 2,                                           (5)

или E+1 - Ei |< 5 2, i = 2, 3, ..., где 51 > 0 и 52 > 0 - выбранные пользователем достаточно малые уровни значимости критериев. В отличие от модели тренда, финальную оценку меры волатильности НВР рассчитывают по мультипликативной формуле

I

v( n) = л/Пv2 ( n ).

V i = 1

Очевидно, что центрированная и нормиро- ванная структурные компоненты

- ( n) = r (n) / v ( n)

ВЕСТНИК 2013 № 4

представляет собой временной ряд, стационарный по критериям тренда и волатильности.

Оптимальное начальное значение параметра сглаживания s1 в рассмотренной выше рекуррентной процедуре оценки волатильности НВР будем выбирать в соответствии с критерием регуляризации, аналогичным (4). Компоненты штрафа DRF за сложность локально взвешенной полиномиальной регрессии в этом случае приоб- ретают вид

N

DR = ^ X- ^{- 2} ( n ); ^DF =

N n = 1

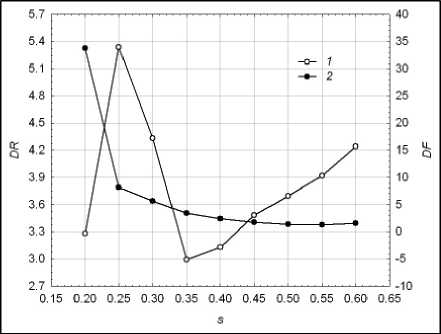
Рис. 17. Зависимости компонентов штрафа от параметра сглаживания модели Lowess: 1 – дисперсия ошибки аппроксимации квадрата остаточного НВР; 2 – дисперсия ошибки локально линейного прогноза меры волатильности

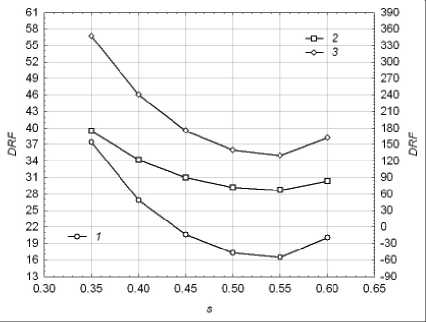
Рис. 18. Зависимости штрафа от параметра сглаживания в модели Lowess для оценки меры волатильности: 1 – γ = 10; 2 – γ = 50; 3 – γ = 100

Зависимости этих составляющих и целевой функции от параметра сглаживания s ₁ для модели Lowess представлены на рис. 17 и 18, соответственно.

Штраф DRF на рис. 18 для значения веса γ = 10 измерен по левой вертикальной шкале, а для весов γ = 50 и 100 – по правой шкале. В вычислительном эксперименте выполнялись три итерации робастного взвешивания Хубера. Параметры правила (2) управления локальным сглаживанием сведены в таблицу 5.

Таблица 5

Параметры управления рекуррентным сглаживанием в модели Lowess для оценки волатильности

N - 2

N

Z ( A ² v ( n ) ) .

n = 3

s 1	S max	I	E 1	EI
0,2	0,6	10	1367,6288	0,000953
0,25	0,65	13	1377,9393	0,000512
0,3	0,7	15	1377,4365	0,000570
0,35	0,75	10	1387,0383	0,000388
0,4	0,8	8	1375,1016	0,000521
0,45	0,8	22	1373,9722	0,001165
0,5	0,8	23	1370,7831	0,001605
0,55	0,8	20	1351,5053	0,001988
0,6	0,8	20	1323,5300	0,002489

Четвертый и пятый столбцы таблицы содержат значения критерия (5) для начальной v 2 ( n ) и финальной v 2 ( n ) остаточной меры волатильности. Процесс сходимости остаточных мер волатильности v i ² ( n ) , 1 <  n <  N к единичному уровню в метрике Евклида по итерациям i алгоритма рекуррентного сглаживания демонстрирует рис. 19. Наибольшее абсолютное отклонение финального НВР v 2 ( n ) , 1 <  n <  N от единицы не превышает величин 0,007182 и 0,029608 для значений параметра сглаживания s ₁ = 0,35 и 0,55.

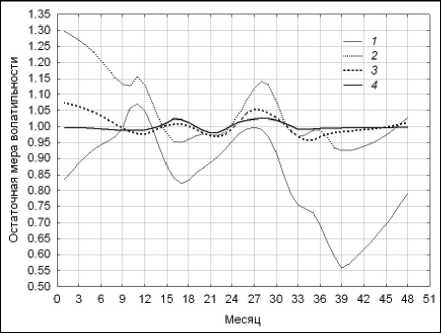
а) s ₁ = 0,35

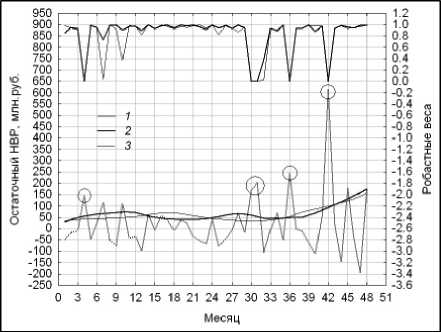
Рис. 20. Меры волатильности при сглаживании с помощью модели Lowess: 1 – r ( n ) для s ₁ = 0,425; 2 – ν ( n ) для s ₁ = 0,35;

3 – ν ( n ) для s ₁ = 0,55

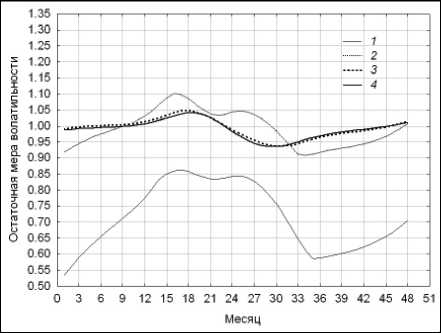
а) s ₁ = 0,55

Рис. 19. Сходимость остаточных мер волатильности к единичному уровню: 2222

V 2 ( П ) ; V 3 ( П ) ; ^J V 5 ( П ) ;        V 7 ( n )

ВЕСТНИК 2013 № 4

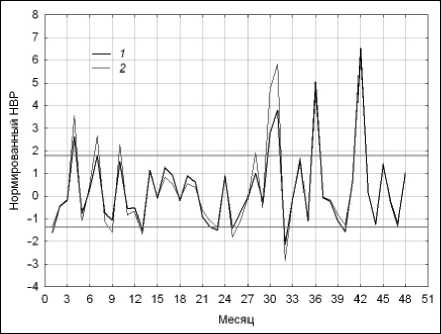
Рис. 21. Оценки центрированного и нормированных рядов при сглаживании с помощью модели Lowess:

1 – s ₁ = 0,35; 2 – s ₁ = 0,55

Финальные оценки меры волатильности v ( n ) , 1 <  n <  N консолидированных поступлений в московский бюджет от ОНР для указанных выше параметров модели сглаживания Lowess представлены на рис. 20. Робастные веса Хубера измерены по правой вертикальной шкале. Соответствующие оценки центрированного и нормированного временных рядов z ( n ) , 1 <  n <  N иллюстрирует рис. 21. Более предпочтительным, на наш взгляд, является выбор s 1 = 0,425 и 0,35 при анализе тренда и масштаба данных.

Альтернативные DEWR-оценки меры волатильности консолидированных поступлений в бюджет г. Москвы от ОНР демонстрирует рис. 22. В вычислительном эксперименте выполнялось рекуррентное сглаживание квадрата центрированного ряда r ( n ) , 1 <  n <  N , полученного с помощью модели DEWR с параметрами s 1 = 0,35 и X = 0,1 (рис. 16). Предпочтительными, по нашему мнению, являются следующие параме-

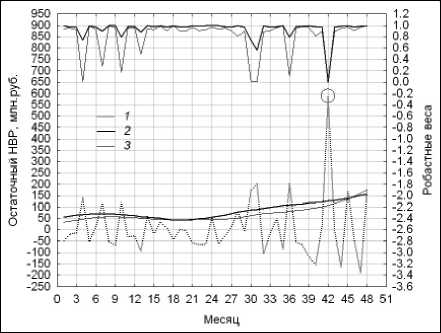
Рис. 22. Меры волатильности при сглаживании с помощью модели DEWR:

1 – r ( n ) для s ₁ = 0,35 и λ = 0,1; 2 – ν ( n ) для λ = 0,1;

3 – ν ( n ) для λ = 0,25

тры управления локальным сглаживанием ряда r ² ( n ) : 5 1 = 0,35, A 5 = 0,05; S max = 0,75, I = 48. Наибольшее количество итераций робастного взвешивания Л.Д. Мешалкина не превышало 10.

Сходимость по критерию (5) текущей меры волатильности v ² ( n ) , 1 <  n <  N к единичному уровню в метрике Евклида за двадцать итераций 2 <  i <  20 иллюстрирует рис. 23. Наибольшее абсолютное отклонение финального НВР v 4 ₈ ( n ) , 1 <  n <  N от единицы не превышает величин 0,006273 и 0,000856 для значений параметра устойчивости статистик X 1 = 0,1 и 0,25. Соответствующие DEWR-оценки временного ряда z ( n ), 1 <  n <  N представлены на рис. 24. В итоге приемлемый, на наш взгляд, выбор параметров DEWR модели сглаживания при анализе меры волатильности консолидированных поступлений в московский бюджет от ОНР состоит в следующем: 5 1 = 0,35 и X = 0,1.

ВЕСТНИК 2013 № 4

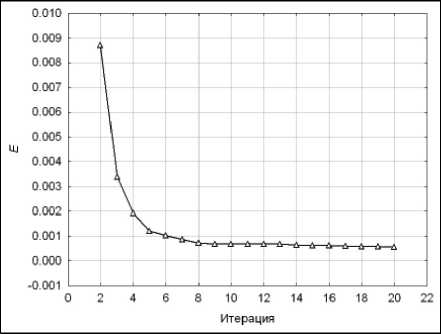
Рис. 23. Сходимость рекуррентной процедуры оценки волатильности НВР с помощью модели DEWR для s ₁ = 0,35 и λ = 0,1

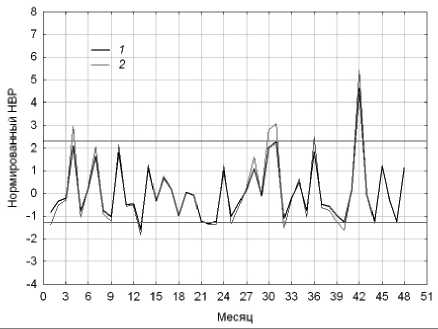
Рис. 24. Оценки центрированного и нормированного рядов z ( n ) при сглаживании с помощью модели DEWR для s ₁ = 0,35: 1 – λ = 0,1; 2 – λ = 0,25

Кластеризация доходности ОНР

Дальнейшее исследование динамики поступлений от рекламы связано с анализом статистик центрированного и нормированного временных рядов z ( n ) , 1 <  n <  N . В частности, практический интерес представляет изучение корреляционных зависимостей этого ряда. Анализ формы диаграмм рассеяния для значений корреляционных лагов от 1 до 6 показал, что данные не обладают сколько-нибудь выраженным генеральным направлением. Указанное свойство иллюстрирует рис. 25, на котором представлены двумерная и трехмерная диаграммы для лагов двух и шести месяцев. Стандартные выборочные оценки коэффициента корреляции для этих лагов составили величины - 0,229 ± 0,138 и 0,207 ± 0,132, соответственно.

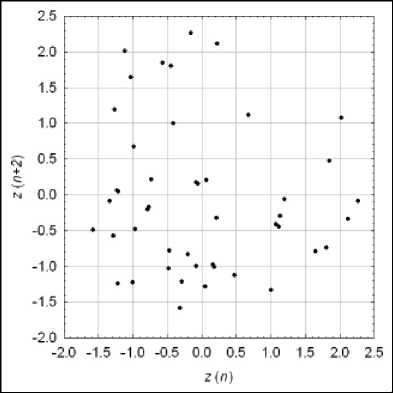
а)

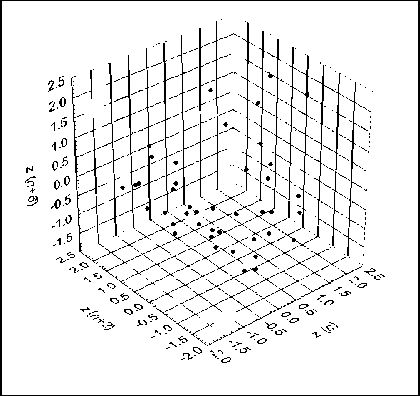
б)

Рис. 25. Диаграммы рассеяния временного ряда z ( n ): а) лаг два месяца; б) лаги два и шесть месяцев

Иными словами, отсчеты временного ряда z ( n ) , 1 <  n <  N практически не коррелированы. Обнаруженное свойство позволяет рассчитать доверительные интервалы и соответствующие им вероятности пребывания ряда в заданном диапазоне его значений. Удобной методической основой такого анализа является гистограмма, сглаженная сдвигом (Average Shifted Histogram – ASH) [8] ₁ m - 1

*-⁾⁼ Ns , 5/ ^(M-^;

z k = z min + ^{k A} z ; ^k = 0, •••, K ;

^K = ( z max - z min )/ ^A z •

Здесь 5 = 2 IQ J 3[N - робастная оценка ши- рины разрядных интервалов (bins) Фридмана –

Дьякониса [8]; IQ – интерквартильный диапазон данных; Az = 5 / m и m - ширина «суженных» интервалов (narrow bins) и их количество; Sl -количество наблюдений, попавших в l-ый «су- женный» интервал (Sl = 0, если l < 0 или l > K).

Окно данных w( j ) выбирают из условия ^mmw( j ) = m. В этом случае гистограмма интегрируема с единицей. Такой нормировке удовлетворяет обобщенное окно вида m-1

w ( j ) = m Ker ( j / m ) ^ Ker ( l / m ) .

l = 1 - m

Расчеты выполнялись для центрированных и нормированных временных рядов, полученных с помощью моделей Lowess (рис. 21) и DEWR (рис. 24) с параметрами s 1 = 0,35 и X = 0,1. Пунктирными линиями на указанных рисунках отмечены уровни поддержки ZS и сопротивления ZR , выбранные по критерию робастных весов. В вычислительном эксперименте гистограммы сглаживались окном данных, сформированным на основе трижды взвешенного ядра Епанечникова [8]. Оценки распределений представлены на рис. 26.

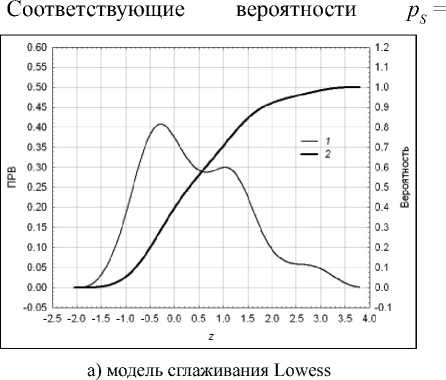
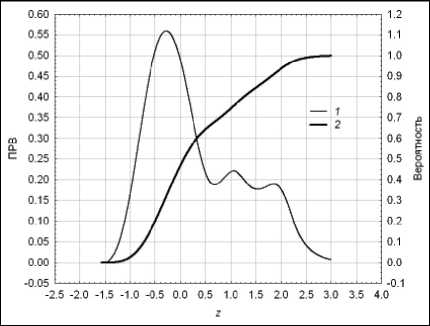
б) модель сглаживания DEWR

Рис. 26. ASH-оценки распределений отсчетов временного ряда z ( n ):

1 – плотность распределения вероятностей (ПРВ);

2 – интегральное распределение

= P { z <  Z S } и p_R = P { z >  Z R } выбросов ряда z ( n ) , 1 <  n <  N за пределы уровней поддержки и сопротивления сведены в таблицу 6. Последний столбец таблицы содержит вероятности

pSR = P { ZS < z < ZR } = 1 — pS - pR для «типичных» значений доходности ОНР.

Таблица 6

Уровни поддержки и сопротивления центрированных и нормированных консолидированных поступлений от ОНР

Модель	Z S	Z R	pS	pR	p SR
Lowess	–1,208046	2,231238	0,0233	0,059472	0,917228
DEWR	–1,214729	2,265476	0,0046	0,026147	0,969253

ВЕСТНИК 2013 № 4

Важно также отметить, что ASH-оценки демонстрируют наличие кластерной структуры данных, а именно наличие трех классов «низкого» – Low, «среднего» – Mid и «высокого» – High уровней консолидированных поступлений от ОНР. Дискриминантные границы этих классов доходности ОНР, сформированные в виде абсцисс ZLM и ZMH локальных минимумов гистограмм, а также вероятности p L = P { z < ZLM } , p M = P { ZLM < z < ZMH } , pH = P { z > ZMH } таких доходностей сведены в таблицу 7.

Таблица 7

Границы классов доходности ОНР

Модель	ZLM	7 MH	pL	pM	pH
Lowess	0,653179	1,967250	0,604889	0,313794	0,081317
DEWR	0,679055	1,533509	0,679603	0,171313	0,149084

Рассмотренная выше методика интеллектуального анализа НВР позволяет формировать прогнозные модели доходности московского рынка наружной рекламы.

ВЕСТНИК 2013 № 4

Адаптивная модель прогнозирования доходности ОНР

Будем предполагать, что изменения основных статистик для поступлений от ОНР г. Москвы достаточно медленные. Такого рода персистентность данных позволяет описывать тренд y ( n) и меру волатильности v( n ) для доходности ОНР с помощью адаптивной модели Хольта (Holt) [10]. В рамках этой модели локально линейные прогнозы y 1 ( n -1) = a 1 ( n -1) + a 2 ( n -1), v1 ( n -1) = b 1 ( n -1) + b 2 ( n -1) указанных выше статистик на один шаг времени рационально рассчитывать в терминах ошибок аппроксимации

n ( n ) = y ( n )^- y 1 ( n ^- 1 ) ,

д( n ) = v (n)-V1 ( n -1), 2 < n < N.

Адаптацию средних значений a 1 ( n ) , b 1 ( n ) и темпов изменения a ₂ ( n ) , b ₂ ( n ) статистик по мере поступления новых оценок y ( n ) и v ( n ) реализует прогнозная форма процедуры экспоненциального сглаживания

a 1 (n) = a 1 (n -1) + a 2 ( n -1) + а1 n( n), a 2 (n) = a 2 ( n -1) + а1 а 2 n( n),

b 1 ( n) = b 1 (n -1) + b 2 ( n -1) + в1 Ц (n),

b2 ( n) = b2 ( n -1) + в1 в2 ц( n).

Здесь а 1 , в 1 и а 2 , в 2 - параметры сглаживания статистик и их первых разностей. Эти параметры удовлетворяют известным ограничениям 0 <  а 1 <  а ₂ <  1 и 0 <  в 1 <  в ₂ <  1 [10]. Относи-

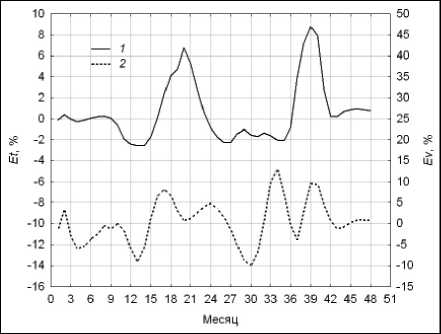
а) модель сглаживания Lowess

б) модель сглаживания DEWR

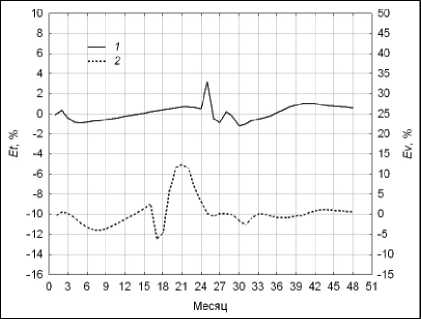
Рис. 27. Относительные ошибки аппроксимации статистик: 1 – тренда; 2 – меры волатильности тельные ошибки аппроксимации

Et ( n) = 100 n( n)/y ( n),

Ev ( n ) = 100 ^v ( n), 2 < n < N тренда и меры волатильности, полученные с помощью процедур рекуррентного сглаживания Lowess и DEWR, демонстрирует рис. 27.

Сравнение рисунков свидетельствует о том, что модель Хольта аппроксимирует DEWR-оценки статистик с меньшими ошибками. Соответствующие оптимальные значения параметров модели Хольта сведены в таблицы 8 и 9.

Таблица 8

Параметры модели Хольта для аппроксимации тренда

Модель	a 1(1)	a 2(1)	α 1	α 2
Lowess	210,1	1,025	0,736	1
DEWR	205,3	4,495	0,772	1

Таблица 9

Параметры модели Хольта для аппроксимации волатильности

Модель	b 1(1)	b 2(1)	β 1	β 2
Lowess	20,61	9,712	0,681	1
DEWR	53,81	3,173	0,396	1

Актуальные линейные прогнозы тренда и меры волатильности НВР на заданное количество m шагов времени приобретают вид

ym ( N ) = a 1 ( N) + ma 2 ( N) ,

vm ( N )= b 1 ( N ) + mb 2 ( N) .

Соответствующие прогнозы

x m ( n ), x m ( n ), x mM ( n ), x MH ( n )

характерных уровней доходности ОНР вычисляют по формуле

x (Л N ) = У m ( N ) + Z ( . ) v m ( N ) , где под символом ( * ) подразумевают один из четырех индексов S , R , LM , MH уровней доходности ОНР, представленных в таблицах 6 и 7.

Важно отметить, что каждому уровню x m ( N ) , x m ( N ) или x mM ( N ) , x MH ( N ) отвечают свои вероятности p_S , p_R , p_SR или p_L , p_M , p_H попадания доходности в соответствующие доверительные интервалы. В этом смысле прогнозные оценки уместно интерпретировать как интервальные. Результаты такого рода прогнозирования на три месяца ( m = 3) поступлений в бюджет г. Москвы от ОНР с помощью моделей Lowess и DEWR иллюстрируют рис. 28.

Сравнение рисунков свидетельствует о том, что модель Lowess формирует несколько завышенные оценки тренда и меры волатильности для правого сегмента данных.

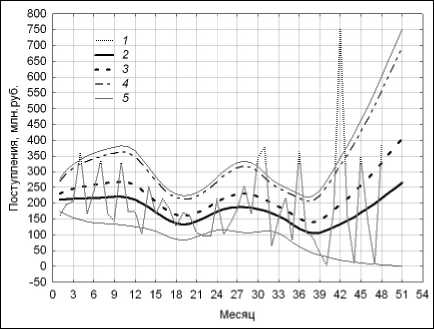
а) модель сглаживания Lowess

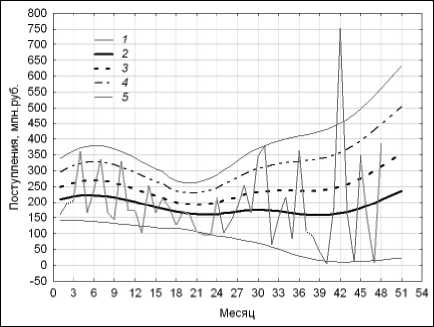
б) модель сглаживания DEWR

Рис. 28. Прогноз рынка наружной рекламы:

1 – консолидированные поступления в бюджет; 2 – тренд;

3 – граница «низкой/средней» доходности;

4 – граница «средней/высокой» доходности;

5 – линии поддержки и сопротивления

Заключение

В работе представлена методика интеллектуального анализа данных на примере исследования основных статистик и прогнозирования НВР в виде поступлений в бюджет г. Москвы от ОНР. Продемонстрирована возможность и эффективность оценивания тренда и меры волатильности рынка наружной рекламы с помощью моделей локально взвешенной робастной регрессии и процедуры рекуррентного сглаживания выборочных данных малого объема. Исходя из гипотезы медленного изменения статистик НВР, сформированы интервальные краткосрочные прогнозы динамики поступлений в рамках адаптивных эконометрических методов.