Анализ динамики ротора турбокомпрессорана подшипниках скольжения с плавающими втулками

В высокооборотных роторах турбокомпрессоров наддува дизельных двигателей широкое применение получили подшипники скольжения с плавающей втулкой. Введение в конструкцию подшипника плавающей втулки и второго смазочного слоя привело к появлению в системе устойчивого предельного цикла, размеры которого удовлетворяют условиям работоспособности подшипников в широком диапазоне рабочих частот вращения ротора. Появление в системе устойчивого предельного цикла открыло возможности управления его размером путем выбора конструктивных и режимных параметров ротора и гидродинамических опор с плавающими втулками на ранних этапах их проектирования. В большинстве работ расчет амплитуд устойчивых предельных циклов и нагруженно сти подшипников выполняют с использованием модели «автономной опоры», содержащей две массы (цапфу и втулку) и два смазочных слоя, исключая вал, связывающий два подшипника. Однако такой подход не позволяет определять форму установившегося движения ротора, обусловленную взаимосвязью ротора и обоих подшипников в единую систему.

Модели многомассовых гибких роторов на двух подшипниках с плавающими втулками использовали C.-H. Li [1], A. Boyaci [2], B. Schweizer [3, 4], C. Holt [5], что позволяло расчетным путем исследовать форму установившегося движения ротора и ее влияние на нагруженность подшипников. Однако этот вопрос в указанных работах не рассмотрен.

Поэтому исследование формы установившегося движения единой системы «ротор – подшипники с плавающей втулкой» и ее влияния на нагруженность подшипников представляется актуальным.

Модель ротора

Ротор турбокомпрессора наддува дизельного двигателя приведен на рис. 1. Он представляет собой вал, на котором консольно закреплены колесо компрессора и колесо турбины. Вал опирает-

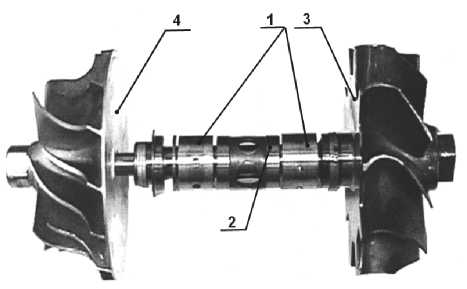
Рис. 1. Ротор турбокомпрессора ТКР-8,5С: 1 – плавающие втулки; 2 – дистанционная втулка; 3 – колесо турбины;

4 – колесо компрессора

ся на два подшипника скольжения с плавающими вращающимися втулками. Каждый подшипник содержит два смазочных слоя. В корпусе подшипника и втулки предусмотрены отверстия для подачи смазочного слоя. Рабочая частота вращения ротора составляет 70 000 об/мин.

Расчетная дискретная модель ротора на подшипниках с плавающими втулками приведена на рис. 2. Независимо от жесткости опор форма вынужденных колебаний ротора в технически реализуемом диапазоне частот вращения определяется вкладом лишь первых двух его изгибных собственных форм. Для их учета до статочно использовать дискретную модель ротора с малым числом степеней свободы.

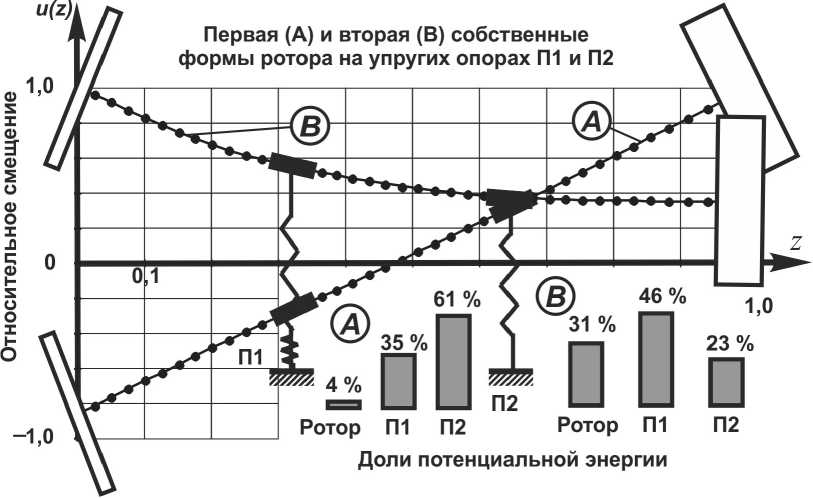
Дискретная модель ротора (рис. 2) построена с использованием аналогии между задачей определения величин ее масс и математической задачей построения интерполяционной квадратурной формулы с заданными узлами. Этот метод позволил обеспечить высокую степень динамического подобия дискретной модели континуальному прототипу при использовании всего лишь 4 сосредоточенных масс. На рис. 3 приведены две низшие собственные формы конечноэлементной (показаны точками) и дискретной (показаны сплошной линией) моделей.

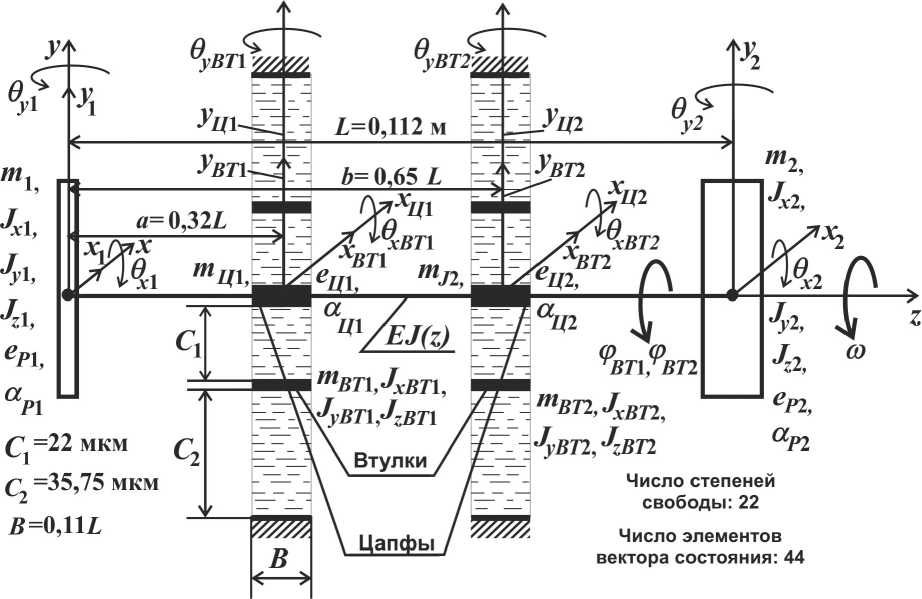
Рис. 2. Расчетная дискретная модель ротора на подшипниках с плавающими втулками

Собственные частоты

	Модели ротора
е е е	С распределенной массой	118,355 Гц	340,827 Гц
	Дискретная модель	118,353 Гц	340,531 Гц

Рис. 3. Собственные частоты и формы континуального ротора и его дискретной модели

Эти собственные частоты и формы найдены при жесткостях опор, линеаризованных в установившемся режиме на рабочей частоте вращения.

Система уравнений

Систему уравнений модели «ротор – подшипники с плавающей втулкой» («ротор – ППВ») образуют уравнения движения цапф (1), дисков (2), и втулок (3):

• е m Цk x Цk

= SFxi" ^ki + Пк • SMyi + Пк • SТУк + RXк + тцкецк®2 cos(®t + «Цк ), i=1                       i=1                  к=1

• е тЦк yЦк

= S F yi • ^ - П к • S M xi - П к ' S T k + R5+ ^т цк ^е цк ® ² sin ( ® t + « Цк ) - ^т цк д . i = 1                        i = 1                  к = 1

i b - l         l - a i               «2.

^{Х -}1 ^Х Ц 1 ' T— ^{+ Х} Ц 2 • T— l = S «j F ⁺ S Pij M yj , \ ba      ba j j = 1        j = 1

^х ц 2 ^х ц 1 b - a

= S YijFxj +S 5ijMyj , j=1           j=1

y -1 У ц 1 • b -^ + У ц 2 • =-a l- S "  F + S W .

V b - a        b - a j j = 1          “1

_ уц 1  уц 2 = zy zy xi к „ S' j У ' S ij xj ’ b - a      j=1          j=1

_т у       D( ²⁾ _ D^{( 1 )}

^т ВТк ^Х ВТк = ^rx1  ^rx1 .

D ( 2 ) z>( 1 )

^m ВТk У вТk = R i ^- R y^ ^- m BT^ g .

J Д _ T ^{( 1)} _ T^{(2 )}

J 2ВТХ ^ф Х = ^TzX   ^TzX .

ее

^J yВТk9yВТk , J хВтк^лВтк

г ⁽²⁾ _ tM ykyk ^,

-(2) _ yX1)

xkxk

в которых учтены гироскопические моменты и инерционные нагрузки (4)

^F xj = ^- m j ^X j ⁺ m j e Pj® ² cos ( ^ t ^{+ a} Pj ) ,         ^M yj = ^- ( ^J yj9yj ^- J zj ®^ ) jj ) ,

^F yj = - m j y j ⁺ m j e Pj® ² sin ( ® t ⁺ “Pj ) - m j g ,   ^M xj = ^- ( ^J xj6jj ^{+ J} zj®9yj ) .

и реакции, действующие на цапфы и втулки со стороны внутренних и внешних смазочных слоев

Т?(1)

xk yk

т ^{( 1 )} xk yk

Т?(2)

xk yk

т ^{( 2 )} xk yk

^R X_k^ _yk f ^х цк ^Х ВТк . ^х цк ^х ВТ к ’^yЦк ^уВТ1 ’ ^уЦ1 ^y EiTk ^ ®ВТ к ’ ФвТк .

е                    е

е                     е

т ( 1 ) I с; ^тхк.ук V ^y

* л*    е z>*/-> л*    е

9 у   УВувтх ■• У-   УВ)>втх ■• У_х   ХВвтк ’ У_х   ХВвтк

1 2 ^{( 2 )}

^хк . у¹ (              •                           а а е е \

( ₂ ) ( ^Х ВТк . ^у ВТк . ^Х ВТк . ^у ВТк . ^Ю ВТк ^ф ВТк Хв_хВТк УВ)>ВТк Хв_хВТк У\ТВ1 к ) •

^T xk yk

,

Вектор состояния системы содержит 44 элемента, 28 из которых (линейные и угловые перемещения и скорости цапф и втулок) входят в правые части уравнений Рейнольдса [6]

d

hl д р к s )

^d ^ ( ¹² ^ Is ^дФ

d +

hl д Р кs )

S z s ( ¹² M is

'^zs j

= 2 Z ks ^G ks ^sin ( ф ^- S is ) ^- 2 E hs cos ( ф ^- 5 к _$ ) +

+ 2E1 Asz^cos(ф - SIs )- 2G1 Aszs ^^^sin(ф - SIs ), 2as2as из решения которых определяются [7] эпюры избыточных давлений а их интегрированием – реакции и моменты внутренних (s) = (1) и внешних (s) = (2) смазочных слоев (7)

R ^{( s} ) ^R x^k

R ⁽ s )

L ку1 J т (s) Txk

M0to B_s D,

^s ²

•

51- JJ рк l(P. zs )

4 a_{s S}

cos ( ф ) sin ( ф )

d ^ dz s

Ho® B s D s

т ( s ) _ ^ту1

уУ

8 0 7 JJ ^z • ^{p k} s ^{)( ₽} . z s )

cos ( ф ) sin ( ф )

d ф dz_s .

В выражениях (1)-(7) приняты следующие обозначения:

• x ,    у , z - декартова система координат, в которой определяются перемещения и углы поворота элементов дискретной модели;

• i,    j = 1,2 - индексы, соответствующие дискам компрессора (1) и турбины (2);

к = 1 , 2 - индексы, соответствующие опорам ротора;

m i , т ц _к , т_ВТк - сосредоточенные массы дисков, цапф и втулок;

J_xi , J yi , J_z i , J_xВTk, J_yBTk, J_zВTk - массовые моменты инерции дисков и втулок относительно осей x , y , z ;

• x i ,    y i , х ц _к , у ц _к , x_BTk , у_ВТк - абсолютные смещения геометрических центров дисков, цапф и втулок вдоль осей x и у ;

O x, , О у , 0_xВTk , 0_уВТк - абсолютные углы поворота дисков и втулок вокруг осей x и у ;

• x i , y i , O xi , 9 * - смещения и углы поворота сечений ротора как абсолютно твердого тела

x i , у i , 0 _xi , 9 у - перемещения и углы поворота i -го сечения ротора вокруг осей x и у , обусловленные его изгибом;

e_Pi , е ц _к, a_Pi, а ц _к - эксцентриситеты неуравновешенных дисков и цапф ротора и фазовые углы, отсчитываемые от оси х против часовой стрелки;

го - угловая частота вращения вала вокруг оси z ;

го _{2 к} - угловые частоты вращения втулок вокруг их геометрических центров;

ф_к - углы поворота втулок вокруг их геометрических центров;

a j , в у , Y ij , д у - статические коэффициенты влияния вала в плоскости zx ;

a Z , p j , y j , 3 j^y - статические коэффициенты влияния вала в плоскости zy ;

F xj , М у , F_y j , M x - силы и моменты, действующие на вал со стороны дисков;

F exj , F_ey j , F exuy , F e _У ц _k - силы инерции неуравновешенных дисков и цапф;

F exвтk , F eyвтk = 0 - силы инерции втулок;

• R^ ), R ук - реакции, действующие со стороны внутреннего смазочного слоя на цапфу и втулку;

R xк ^, R ук ) - реакции, действующие со стороны внешнего смазочного слоя на втулку и на корпус подшипника;

⁽^) тРР              уО) тАР

Txk , Txk , Тук , Тук , т^к , т^к    моменты трения вокруг осей x, у и z, действующие на к ю втулку со стороны внешнего (1) и внутреннего (2) смазочных слоев;

• a , b - осевые координаты первой и второй опор ротора;

l i - осевые координаты дисков, 1 1 = 0;

t - время;

g - ускорение свободного падения;

E k _s = 2 х к - параметр, характеризующий безразмерные скорости движения х к$ вдоль линии центров к -го шипа относительно к -й втулки ( s = 1) и к -й втулки относительно корпуса ( s = 2);

G_ks = ®к — 2 3 S - параметр, характеризующий угловые скорости 3 _s вращения линии центров к -й цапфы относительно к -й втулки ( s = 1) и к -й втулки относительно корпуса ( s = 2);

X _к 1 = ( A x ц_к cos З _к 1 + А у ц_к sin З _к 1 ) / ® С 1 - безразмерная скорость движения цапфы относительно втулки вдоль линии центров;

^кк2 =(-xвтк cos8k2 + уВтк sin§к2) / ®С? - безразмерная скорость движения втулки относитель но корпуса вдоль линии центров;

3 _к 1 = ( -А; к ц_к sin З _к 1 +А у ц_к cos З _к 1 ) ^®е _к 1 - безразмерная угловая скорость вращения линии центров шипа относительно втулки;

З к ₂ = ( - 5с_вт. sin З к ₂ + у_ВТ к cos 3 k ₂ )/ ^ е к ₂ - безразмерная угловая скорость вращения линии центров втулки относительно корпуса;

® к 1 = ( ® — ® _ВТ к ) / ® - безразмерная угловая скорость вращения цапфы относительно втулки;

® k 2 = ® BTk / ® — безразмерная угловая скорость вращения втулки;

G 1 ks = ® ks — 2 Ё ks — параметр, характеризующий скорость вращения плоскости перекоса;

E 1 ks = 2 d" ks - параметр, характеризующий безразмерные скорости движения т ks геометрических центров торцов цапф относительно торцов втулок вдоль линии, соединяющей геометрические центры торцов к -й цапфы и к -й втулки ( s = 1) и геометрических центров торцов втулок вдоль линии, соединяющей геометрические центры торцов к -й втулки и корпуса ( s = 2);

e _k 1 = 0 * = ( у ц 1 - у ц ₂ )Д b - a ) - угол поворота ротора как абсолютно твердого тела вокруг оси х ;

е_к2 = 9 xs _Tk — угол поворота оси к -й втулки вокруг оси х ;

Ёк 1 = 9X /^ = ( уц 1 - уц 2 )Д®-( b - a)] — безразмерная угловая скорость ротора как абсолютно твердого тела вокруг оси х;

*

£ к 2 = 9 _XBTkI ® — относительная угловая скорость к -й втулки вокруг оси х ;

Ах0-2 = хВТ- - 9уВТк • Bl2, Ay0-2 =(yBT- + 0хВТк • В/2) - горизонтальное и вертикальное пере мещения геометрического центра торца к-й втулки относительно корпуса;

А х 0 k 1 = ( х Ц - 9 , • В! 2 ) -A x 0 k 2 ,

А У 0 k 1 = ( У » + 9 X • В /2 ) -А у 0 k 2

- горизонтальное и верти-

кальное перемещения геометрического центра торца к -й цапфы относительно торца к -й втулки;

е 0 ks = ^А х 0 k + А у 0 2s - смещение геометрического центра к -й цапфы относительно геометрического центра к -й втулки ( s = 1) и геометрического центра торца к -й втулки относительно корпуса ( s = 2);

^T ks = V( ^{A x 0} ks ) ^{2 +} ( ^А У ⁰ ks ) ² C s_s - безразмерное перемещение геометрического центра торца к -й цапфы относительно торца к -й втулки ( s = 1) и торца к -й втулки относительно корпуса ( s = 2);

т - । = ( A X 0 _l cos р - । +А у '0 | 81п P k । ) / ® Q - безразмерная скорость движения геометрического центра торца цапфы относительно геометрического центра торца втулки вдоль линии центров;

т k 2 = ( A X 0 2 cos P k 2 + A y 0 2 sin P k 2 ) / ^^ 2 - безразмерная скорость движения геометрического центра левого торца втулки относительно корпуса вдоль линии, соединяющей их центры;

^cos P ks = ^{A x 0} ks I e ⁰ ks , ^sin P ks = ^А у ⁰ ks / e ⁰ ks , - величины, определяющие углы наклона e k 1 , e k 2 линий центров на торцах к -й цапфы и втулки.

• ⁹ Х = ( у ц 1 ^- у ц 2 )/( b ^- a ) , ⁹ У = ( ^{- х}Ц 1 ^{+ х}Ц 2 )/( b ^- a ) , § 1 i =⁽ b - li )^ b - a ) , § 2 i =⁽ l i ^- a V( b ^- a ) , П к = (^{- 1} ) k l b b ^- a ) , h ks = ^{1 -} % ks • ^{cos (}ф ^{- 5} ks ) , M ks = M ks ¹ 0 0 , p k^s ) = P k^{s ) ф} , zs ) • v! I ( 0 0 ® ) , z s = z s ¹ r s , ^V s = ^Cs ¹ r s , ^X ks = ^eks ^{1 C}s , e k 1 = -\/ ^{A x}ц ^{+ A} У ц- , e k 2 = V ^XBTk ^{+ у}ВTk , ^{A x} ц- = ^XLk ^{- X}BTk , ^{A y}Lk = ^уЦк ^{- y}BTk , ^{A X}Lk = ^XLk ^{- X}BTk ^A y Lk = ^yLk ^{- y}BTk , ^cos ^ k 1 =^{A x}Lk/^ek 1 , ^sin ^ k 1 =^{A у}Цк/^ек 1 , ^cos ^ k 2 = xBTkle k 2 , ^sin 5 - 2 = yBTklek 2 .

Уравнения Рейнольдса (6) с учетом перекосов цапф во втулках и втулок в корпусе получены при основных допущениях гидродинамической теории смазки, дополненных допущениями абсолютной жесткости цапф и втулок, и решаются при условиях Свифта - Штибера (8) с учетом источников для подачи смазки:

P k s ) ( ф , ^z s ) = P ks ) ( ф ^{+ 2п}^^z s ) , P k^s ) ( ф , z s ) = p / ^V ф , z ^£Г Y .

• p ks ) = ⁰ , при z s =± ^a s ,

_Pks) (ф,zss )^ 0 на S, замыкающих систему выражений (2)-(7).

Алгоритм расчета

На первом этапе выполнены расчеты для следящей опоры - без учета перекоса втулки относительно ротора и корпуса. Решение уравнений (1)-(7) выполнено интегрированием по времени от начальных условий до установления колебаний методом Рунге - Кутты - Мерсона с перемен- ным шагом. Для решения уравнений Рейнольдса использованы аналитические аппроксимации, приведенные в работе [8], и адаптивный многосеточный алгоритм [9].

Практически вся вычислительная трудоемко сть при интегрировании системы уравнений движения (2)–(3) заключена в пятикратном решении уравнения Рейнольдса для каждого из 4 смазочных слоев на каждом шаге по времени. Поэтому представляется рациональным использование приближенных методов расчета реакций для поиска вектора состояния, близкого к установившемуся режиму.

В качестве приближенного метода расчета опорных реакций использованы аналитические аппроксимации реакций смазочного слоя [6]. Использование этих зависимостей позволило быстро найти установившийся режим и использовать его в качестве начального приближения для дальнейшего уточненного расчета.

Численные эксперименты показали, что интегрирование с переменным шагом при величине погрешности ε = 10^–3, определяющей величину текущего шага по времени, приводит к занижению амплитуд установившихся колебаний примерно на 6 %. Поэтому расчеты динамики ротора выполнены при величине ε = 10^–5…10^–6.

Выполнено две серии расчетов установившихся режимов модели ротора, приведенной на рис. 2, в широком диапазоне частот вращения от 0 до 150 000 об/мин. В каждом расчете задана постоянная частота вращения и выполнено интегрирование по времени от начальных условий до установления колебаний.

Результаты первой серии расчетов

В первой серии расчетов использована идеальная модель подшипника, без отверстий, темпе- ратуры в смазочных слоях приняты постоянными.

В установившемся режиме найдены линеаризованные жесткости опор, определены собственные частоты и формы изгибных колебаний и построена диаграмма Кэмпбелла (рис. 4).

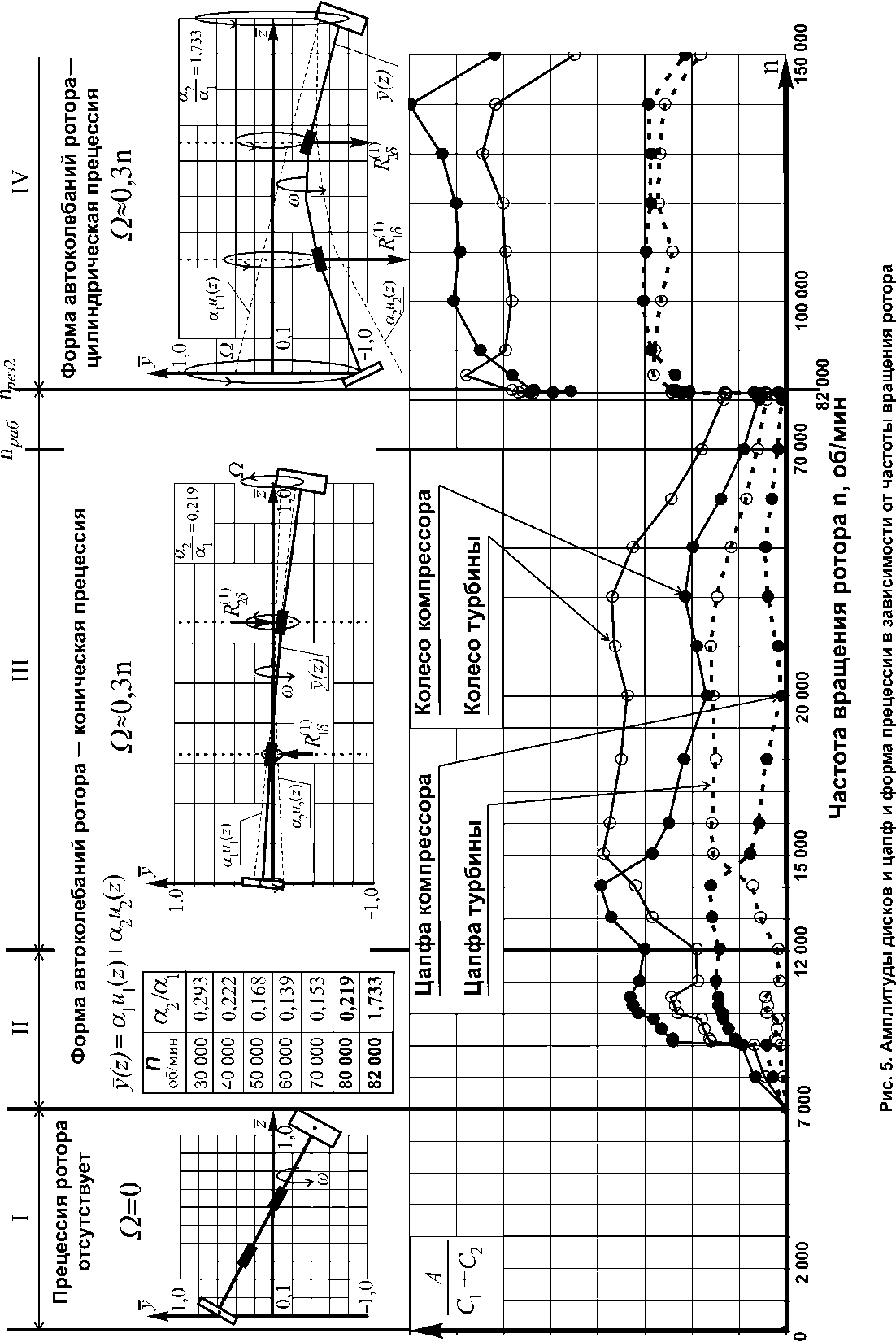
Выполнен анализ формы движения ротора (рис. 5). На малых частотах вращения от 10 до 7 000 об/мин реакции, действующие на цапфы со стороны внутренних смазочных слоев, вертикальны и удовлетворяют условиям статического равновесия ротора.

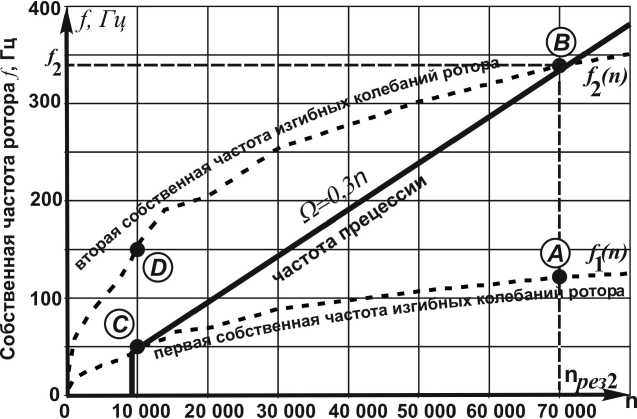
Частота вращения ротора п, об/мин

Рис. 4. Диаграмма Кэмпбелла

С ростом частоты вращения ось ротора поворачивается и ротор занимает почти горизонтальное положение. При дальнейшем увеличении частоты вращения в компрессорной опоре начинаются автоколебания и ротор начинает совершать прецессию с частотой Ω ≈ 0,3n (начало зоны II). В турбинной опоре, нагруженной значительно бóльшими силами веса, автоколебания еще отсутствуют. Около частоты 12 000 об/мин в автоколебания вовлекается цапфа турбины, так что в зоне III ротор представляет собой систему двух связанных через него автоколебательных подсистем (подшипников с плавающими втулками).

При увеличении частоты вращения свыше 15 000 об/мин форма колебаний в зоне III, несмотря на удаление от первой резонансной частоты, остается конической вплоть до 82 000 об/мин. На 82 000 об/мин при переходе через вторую резонансную частоту форма прецессии скачком изменяется на цилиндриче скую. На этой же частоте происходит резкое увеличение амплитуд колебаний ротора и нагруженности подшипников. При этом амплитуды колебаний ротора и нагрузки на подшипники, резко возросшие на второй резонансной частоте nрез2, в зарезонансной области не уменьшаются.

co                  o_                        см иинедэиоя etfAiHuuiAiy

Результаты второй серии расчетов

Вторая серия расчетов выполнена с учетом конструктивных особенностей опор скольжения и изменения температур в смазочных слоях. Результаты расчета приведены на рис. 6. Величина дисбаланса принята равной d 0 = 0,15 г ∙ см, температура подачи смазки равной Т вх = 80 °С, давление подачи – P вх = 0,4 МПа. В результате установлено, что за второй резонансной частотой, расположенной, как и в первой серии, между 80 000 и 85 000 об/мин, внутренний зазор в компрессорной опоре оказался практически полностью выбранным, что недопустимо для подшипников, а расчетная температура в смазочном слое до стигла 200 °С и намного превысила допустимую для смазки величину.

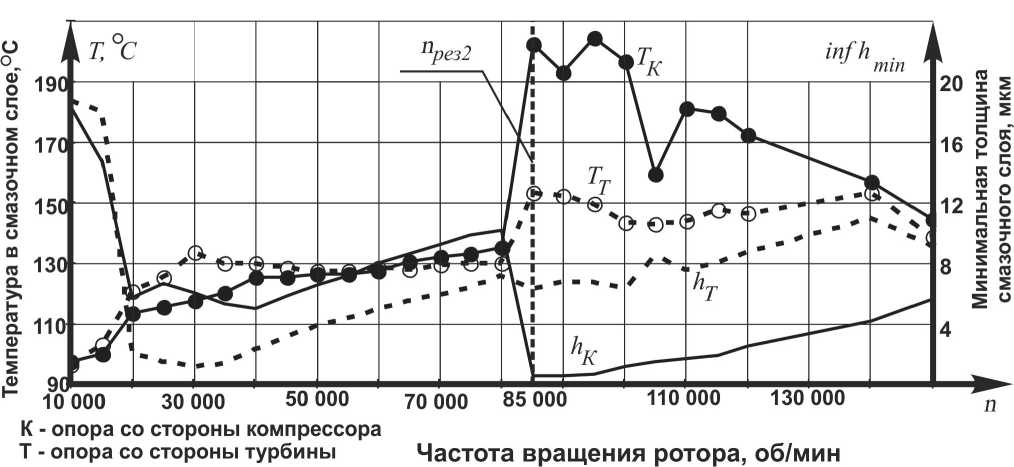
Рис. 6. Минимальные толщины и температуры во внутренних смазочных слоях компрессорной и турбинной опор

Таким образом, найдена частота вращения, при превышении которой ротор на подшипниках скольжения с плавающими втулками становится неработоспособным. Эта частота для рассмотренной конструкции ротора составила около 82 000 об/мин и оказалась до статочно близка к его рабочей частоте 70 000 об/мин.

Заключение

Создан пакет программ, который позволяет рассчитывать установившиеся и неустановив-шиеся режимы движения системы «ротор – подшипники скольжения с плавающей втулкой» с учетом конструктивных особенностей опор скольжения и изменения температур в смазочных слоях. Применение этого пакета позволяет оценивать амплитуды колебаний высокооборотных роторов малоразмерных турбомашин и гидромеханические характеристики их опор скольжения на ранних стадиях разработки новых и модернизации существующих подшипниковых узлов.

• 1.    Предложены алгоритм и программа расчета динамики ротора турбокомпрессора на подшипниках с плавающими втулками. Алгоритм и программа расчета позволяют одновременно учесть упругие и инерционные свойства ротора, реакции смазочных слоев, которые определяются из численного решения уравнения Рейнольдса, и связанность движения ротора и подшипников скольжения с плавающими втулками.

• 2.    Построена дискретная модель гибкого ротора турбокомпрессора с четырьмя сосредоточенными массами. Эта модель динамически подобна ее континуальному прототипу по первым двум изгибным собственным формам. Для построения модели использован научно обоснованный метод, который обеспечил высокую степень динамического подобия при минимально возможном числе сосредоточенных масс дискретной модели.

• 3.    Разработан алгоритм расчета реакций смазочных слоев, состоящий из двух этапов. На первом этапе реакции смазочных слоев и амплитуды предельных циклов определяются в гладком подшипнике по аппроксимирующим зависимостям [8]. Эти результаты используются в качестве начальных приближений на втором этапе. На втором этапе реакции смазочных слоев и амплитуды

• 4.    Установлено, что ротор турбокомпрессора представляет собой сложную механическую систему, включающую в себя две связанные через него автоколебательные подсистемы – подшипники с плавающей втулкой. Показано, что у ротора рассматриваемого типа в практически достижимой области частот вращения существуют две формы прямой регулярной несинхронной прецессии: коническая – с противофазным, и цилиндрическая – с синфазным движением цапф. Переход от конической формы к цилиндрической происходит скачкообразно на второй резонансной частоте вращения ротора n_{рез 2} и сопровождается недопустимым повышением нагрузок на подшипники во всей зарезонансной области. Показано, что резонансная частота вращения ротора турбокомпрессора ТКР-8,5С составляет n рез 2 = 82 000 об/мин и близка к его рабочей частоте n раб = 70 000 об/мин.

• 5.    Обеспечить работоспособность подшипников с плавающими втулками в условиях форсирования рабочих частот вращения роторов турбокомпрессоров возможно лишь за счет повышения второй резонансной частоты системы «ротор – подшипники», что требует максимального увеличения жесткости ротора и подшипников.

предельных циклов определяются с использованием адаптивного многосеточного алгоритма [9, 10], с учетом конструктивных особенностей опор скольжения и изменения температур смазочных слоев. Использование алгоритма, состоящего из двух этапов, позволило на порядок ускорить расчет установившегося режима движения ротора по сравнению с алгоритмом, содержащим только второй этап.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 13-08-00875 А).