Анализ движения клубня по сепарирующей поверхности

Картофель у нас является традиционно ценнейшим продуктом питания, его годовое потребление составляет 120-130 кг на человека. Урожайность картофеля во всех категориях хозяйств в Иркутской области в последние несколько лет мало изменялась и находится на уровне 14-15 т/га. В Бурятии же средняя урожайность культуры последние 20 лет была в пределах 7,8-9,7 т/га, что ниже ее ежегодного уровня в целом по Восточной Сибири примерно на 1020% [1]. Необходимо развивать и совершенствовать российское картофелеводство, повышать качество продукции и технологических процессов.

Однако интенсификация технологических процессов картофелеводства, а особенно рост уровня механизации возделывания и уборки картофеля ведут к увеличению уровня механических повреждений клубней.

Цель исследования. В настоящее время среди основных задач, решаемых при разработке картофелеуборочной техники, стоит проблема создания картофелеуборочных машин, обладающих максимальной сепарирующей способностью при минимальных повреждениях клубней.

Результаты исследования и их обсуждение

Рассмотрим движение клубня по горизонтальной сепарирующей поверхности, предназначенной для выделения почвенных примесей. Частоту вращения роторов горизонтальной части сепаратора желательно установить такой, чтобы достигалось безотрывное движение основной массы клубней по сепарирующей поверхности, при этом одиночные клубни могли бы устойчиво перемещаться без подпора вновь поступающих компонентов, при таком режиме будет происходить эффективная сепарация почвы, а клубни не получат повреждений.

На рисунке приведена схема действия сил на клубень, находящийся на вращающейся наружной грани пальца ротора, при произвольном наложении относительно выбранной си- стемы координат.

Для определения закона движения клубня применим дифференциальные уравнения относительного движения [2]. В проекциях на оси X и У они имеют вид:

mx = P _x - F _da + F nx = mg cos а - F _da + mw ² p cos ^

, my = - Py + N - Fny - FK = - mg sin а + N + mw2 p sin ^ - 2 mwx'

,

J cT" = F _da

• r

,

где Р - сила тяжести клубня; Fnx; Fny - проекции центробежной силы инерции переносного движения на ось X и ось У; N - сила реакции поверхности пальца; Fk - кориолисова сила инерции; т - масса клубня; р - расстояние от центра вращения ротора O1 до центра инерции клубня С; Jc - момент инерции клубня относительно оси, проходящей через центр С, Jc = 0,4 mr2; х' - скорость клубня в относительном движении по поверхности пальца ротора; ρ" -угловое ускорение клубня при перекатывании без скольжения; ω - угловая скорость вращения ротора.

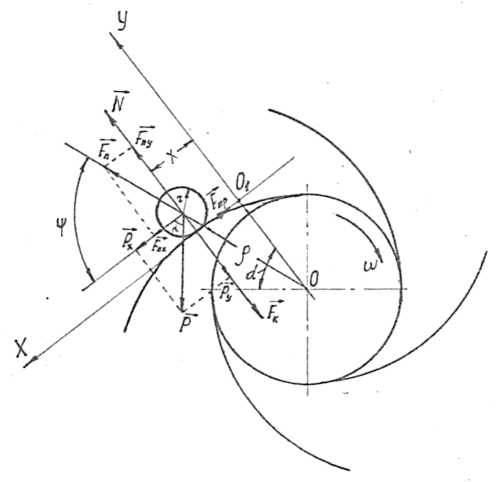
Рисунок - Схема действия сил на клубень

Для упрощения задачи мы приняли допущение, что клубень имеет шарообразную форму.

Примем во внимание, что α = α 0 + ω t ; ρ cos ψ = X; F тр = fN.

Тогда можно записать:

mx = mw ² x + mg cos ( wt + a 0 ) - fN

После преобразования получим следующее неоднородное дифференциальное уравнение движения клубня:

2                     fN x - w x = g cos(wt + a0)-- m .                            (5)

Общее решение неоднородного дифференциального уравнения (5) будет иметь вид:

x = CZ + C₂e ^{- wt} + x.

12  í где xн - частное решение неоднородного уравнения, которое ищется в виде: x^ = C3 cos(wt + a0)+ C4

Подставляя значения Х н по уравнению (7) в уравнение (5), получим:

- C 3 w ² cos ( wt + a 0 ) - w ² C 3 cos ( wt + a 0 ) - C ₄ w ² = g cos ( wt + a 0 )-—

m

Из уравнения (8) можно найти С 3 и С 4 :

C 3

g ; 2 w ²

C 4

fN mw ²

С учетом значений Сз и С4 уравнение (6) - общее решение неоднородного дифференци ального уравнения (5) - примет вид:

x = C 1 e wt + C ₂ e ~ ^wt —g y cos ( wt + a 0 ) + - fN

2 w ²              mw ²

Постоянные C 1 и С 2 определятся из начальных условий:

t = 0, ^x ‘ = 0, X = X o .

Подставляя начальные условия в уравнение (9), получим:

x ₀

= C 1

g cos α ₀    fN

⁺ C 2        2 ⁺     2

2 w ²     mw ²

или, используя производную от X, т.е. от выражения (9):

gw sin α

0 = w ^{( C} 1 ^{+ C} 2 ^{)+ 6}     2 0

2 w ²

Из уравнения (10):

C 1 + C ₂ = x ₀ +

mg cos a ₀ - 2 fN

2 w ²

Из уравнения (11):

= g sin a 0 2 w ²

Сложив правые и левые части уравнений (12) и (13) и проведя преобразования, получим выражение для определения С2:

x 0 mg ( cos a 0 + sin a 0 ) - 2 fN

C I

2          4 mw ²

Тогда выражение для определения C 1 будет иметь вид:

x 0 + mg ( cos a 0 + sin a 0 ) - 2 fN

^{1    2             4 mw 2}            .                         (15)

Подставив значения постоянных из уравнении (14) и (15) в уравнение (9), получим выражение для определения координаты “X” клубня:

[ x 0 mg(cosa 0 — sin a 0 ) — 2 fN

X = I--+--5--------------

V 2          4 mw

cosa 0 + sin a ₀ 4 mw ²

I e

,— wt

—

—

g cos ( wt + a о ) fN

.

2 w ²       mw ²

Для определения координаты "У" клубня, учитывая

x

, что p =----- cos ψ

и α = α o +ωt , можно записать:

my = — mg sin ( wt = a 0 ) + N + mw ² xtg v — 2 mwx'

Из рисунка определятся следующие соотношения:

.

или

⁽ У ^— У о ) 2 ⁺ x 2 = P 2

⁽ У ^— У 0 ^{) 2} = P ^{2 —} x ²

Если p = —x— , то cos ψ

( У — У 0 )² = -Л-cos² ψ

—

x ²

x ² ( 1 — cos ^ )     2 2

——= x ² tg 2 W cos² ψ

xtgv = У ^— У 0^.

Преобразовав выражение (17), учитывая выражение (18) и определив первую производную X по выражению (9), можно записать:

У = — g sin ( wt + a ₀ ) + — + w ² ( y — y ₀ ) — 2 w ² 1 C 1 e ^wt — C 2 e"^wt + — g y sin ( wt + a ₀ )

m                V               2 w 2

. (19)

После преобразования уравнения (19) получим следующее неоднородное дифференци- альное уравнение второго порядка:

У — w ² e = — 2 g sin ( wt + a ₀ ) — 2 C 1 w ² e ^wt + 2 C ₂ w ² e ^wt + —— w ² y ₀

m

Общее решение уравнения (20) будет иметь вид:

wt          wt

5 e + C 6 e   + ^yH

, где Ун — частное решение неоднородного уравнения, которое ищем в виде:

yH = C7 sin (wt + a 0) + C8 , подставив значение Ун по уравнению (22) в уравнение (20), получим:

— C 7 w ² sin ( wt + a ₀ ) — w ² C 7 sin ( wt + a ₀ ) — C 8 w ² = — 2 g sin ( wt + a ₀ ) — 2 C 1 w ² e wt +

+ 2 C ₂ w ² e ^wt +--- w ² y ₀ . m

Из уравнения (23) можно определить С 7 и С 8 :

2 wt />      2 — wt    ^N .     2

g

7        2 ;

w

2 C 1 we — 2 C ₂ we ---+ wy ₀ ^m

8                                 2

w

С учетом значений С 7 и С 8 уравнение (21) примет вид:

2 C 1 w² e wt — 2 C ₂ w² e ~ ^wt — N + w² y ₀

Y = C 5 ewt + C 6 e ~wt +    sin (wt + a 0) +-------------------------m-------- w2                                 w2                  . (24)

Постоянные С 5 и С 6 определятся из начальных условий по методике, использованной выше для нахождения постоянных C 1 и C 2 .

В результате расчетов получим:

C = —

—

g ( sin a ₀ — cos a ₀ ) + 2 C , ( w ² — 2 w ) — 2 C ₂ ( w ² + 2 w ) — N m

2 w ²

C = J 0

g ( 3sin a o

—

—

, cos a 0) + 2 C, (3 w2 — 2 w)— 2 C 2 (з w2 + 2 w)— 3N m

2 w ²

.

Подставив значения С 5 и С 6 из уравнений (25) и (26) в уравнение (24), получим выражение для определения координаты "У" клубня:

/

Y =

+

y ₀

к

J

² к

—

—

g ( sin a ₀ — cos a ₀ ) + 2 C 1 ( w ² — 2 w ) — 2 C ₂ ( w ² + 2 w ) — N

2 w ²

e ^wt +

g ( 3sin a ₀ — cos a ₀ ) + 2 C 1 ( з w ² — 2 w ) — 2 C ₂ ( з w ² + 2 w ) — 3N

2 w ²

e — wt +      ⁽²⁷⁾

. /       \ 2Cw2ewt — 2C2w2e—wt g sin( wt + a0)     1___________2

⁺         2       ⁺                   2

ww

—

N 2

— ^{+ w} J o m

.

В выражение (27) необходимо подставить значения постоянных С 1 и С 2 из уравнений (14) и (15), однако при этом выражение (27) будет слишком громоздким.

Преобразуем выражения для определения С 1 и С , исходя из размеров ротора, характеристики клубней картофеля и значения N ср .

Подставив значения постоянных и произведя вычисления, получим:

3 07

C ₂ = 0,005 + V w ²

^, 0,6176

C1 = 0,005 +    — w2

.

С учетом формул (28) и (29) выражение (9) для определения координаты “X” клубня запишется не в виде (16), а следующим образом:

x = f 0,005 + ^06Г6

к          w 2 7

e w + | 0,005 + ^3,07 | e к         w 7

— wt

—

9/81cos ( wt + 0,523 ) + 0,56

2 w ²

w ²

.

Выражение (27) для определения координаты "У" с учетом приведенных выше значений постоянных и формул (28) и (29) после преобразования будет иметь вид:

У =

+

2,19 - ^f 0,01 + ^1,2352 ) ( w ² - 2 w ) - ^f 0,01 - 6,1 2 4 ) ( w ² + 2 w )

w J         V w

2 w ²

e'w

V                                                            J

2,02 +1 0,01 + 1,2-^ | ( 3 w ² - 2 w ) -1 0,01 -     | ( з w ² + 2 w )

w J           V w

2 w ²

V

J

8,39 +1 0,01 + ^1,2352 | w ² e^wt -1 0,01 - 6,1^ | w ² e~^wt

w J V w

Выводы

Видеосъемка процесса работы сепаратора позволила построить действительные траектории движения клубней. Оптимальной можно считать траекторию при угловой скорости 7 с-1, что соответствует частоте вращения валов сепаратора 67 об./мин.

Перекрытие пальцев роторов горизонтальной сепарирующей поверхности желательно сделать как можно меньше для увеличения живого сечения сепарирующей поверхности и лучшего просеивания почвы, однако минимальное значение перекрытия ограничивается недопустимостью потерь мелких клубней массой более 25 г. С учетом геометрических параметров ротора и клубней величину перекрытия пальцев можно принять равной 25 мм.