Анализ гомогенной модели распределенного центра обслуживания вызовов

В настоящее время в крупных территориально-распределенных компаниях (операторы сотовой связи, ОАО «Ростелеком» и т.п.) для телефонного обслуживания клиентов все чаще стали применяться распределенные центры обслуживания вызовов (РЦОВ), включающие несколько локальных центров в филиалах компании, работающих совместно и обеспечивающих при необходимости перемаршрутизацию поступающих вызовов в другие центры. Вызовы и обслуживающие их операторы являются основными функциональными элементами в модели функционирования РЦОВ. Вызов, поступив в локальный центр обслуживания вызовов (ЦОВ), может сразу же попасть на обслуживание оператору или ожидать в очереди, если все операторы ЦОВ заняты. После завершения процедуры обслуживания оператору автоматически поступает следующий вызов из очереди данного или от других ЦОВ. Если же очередь отсутствует, то оператор становится незанятым до поступления нового вызова. Количество вызовов, поступающих на РЦОВ, меняется в течение всего дня. Для обеспечения заданного качества обслуживания вызовов в РЦОВ требуется определенное количество операторов в ЦОВ и оптимальное распределение поступающей нагрузки между отдельными центрами [1-2]. На практике для реализации наилучшего качества обслуживания вызовов в РЦОВ необходимо распределить поступающую нагрузку по всем ЦОВ в составе РЦОВ таким образом, чтобы минимизировать среднее временя ожидания обслуживания относительно всех вызовов.

Гомогенная модель РЦОВ

Рассмотрим гомогенный РЦОВ, в котором отсутствуют какие-либо координирующие центры и все N ЦОВ равноправны с точки зрения выполняемых функций (см. рис.1).

Рис. 1. Гомогенная модель РЦОВ

Нагрузка, поступающая на РЦОВ, характеризуется интервалами времени между после- довательными вызовами, а ее обслуживание – длительностями обработки вызовов операторами в локальных центрах. В общем случае эти параметры могут быть случайными или детерминированными. В рассматриваемой модели процесс поступления вызовов предполагается случайным, описываемым Пуассоновским распределением интервалов между вызовами, что хорошо согласуется с результатами измерений на практике. Распределение интервалов времени обслуживания вызовов операторами в любом ЦОВ – произвольное, которое может быть задано двумя первыми моментами функции распределения – средним временем обслуживания ^обс/       1 /Ц1 и средним квадратическим отклонением времени обслуживания ^i- Таким образом, отдельный ЦОВ, в котором имеется N операторов, можно представить в виде системы массового обслуживания (СМО) M/G/N в соответствии с обозначением Кендалла-Башарина [3].

При анализе ЦОВ определенную роль играет длина очереди, которая может быть конечной или бесконечной. В рассматриваемой модели используется бесконечная очередь, поскольку предполагается, что количество линий во всех ЦОВ в составе РЦОВ будет достаточным для предотвращения блокировки вызовов.

Сделаем следующие предположения.

• 1.    В составе РЦОВ имеется K ЦОВ.

• 2.    Число операторов в i -том ЦОВ - N _i, i = 1; 2 … K .

• 3.    Производительность одного оператора i -го ЦОВ Ць где/ = 1; 2 ... К.

• 4.    Интенсивность поступления вызовов в i -ый ЦОВ Л, /= 1;2 ...К.

На рис. 2 представлен i -ый ЦОВ из состава РЦОВ, где ^X_K_i – интенсивность дополнительного потока заявок из k -го в i -ый ЦОВ; ^j-k – ин-

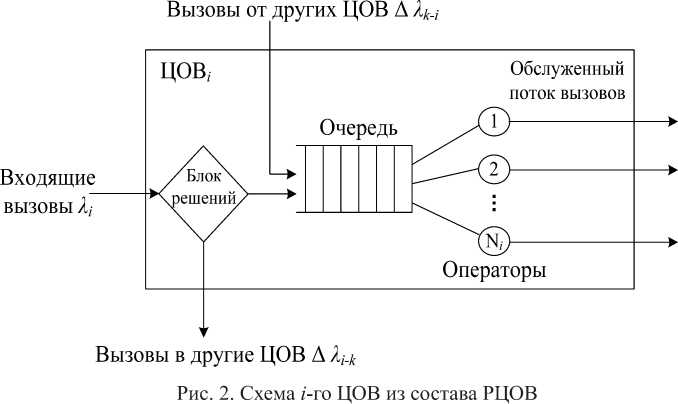
тенсивность дополнительного потока заявок из i -го в k -ый ЦОВ.

Используем формулу Поллячека-Хинчина для определения среднего времени ожидания в СМО M/G/N [3].

т _ ^ож 2{\-рУ

где р =       – коэффициент использования ре-

N • р сурсов ЦОВ (N операторов ЦОВ); N – число опе-

_       1

раторов в ЦОВ; обе          – среднее время

ц -N обслуживания одного вызова в ЦОВ.

Тогда выражение для определения средней длительности ожидания вызовов в очереди для i -ого ЦОВ будет иметь вид

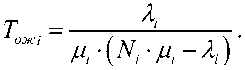
Как было указано выше, для обеспечения оптимальной работы РЦОВ необходимо так распределить поступающую нагрузку по всем ЦОВ в составе РЦОВ, чтобы выполнялось равенство средних длительностей ожидания обслуживания вызовов во всех центрах:

т = т = т ож] ож2 ожЗ

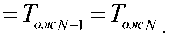
На основе равенства (3) с учетом (2) составим систему линейных алгебраических уравнений:

л

А1 " ( ^1 ' А1 — Д ) Аз ’ ( ^2 ' Аз — Д )

Дд.

Аз" (^2 ’ Аз ^— Д) Аз" (^' Аз ^— У)

ЛЛ

* Аз' (-^з" Аз — ^) А4" ^4 ' Аз — Д)

Ду-1

Ал'-i" (^--1" А.у-i ^— Ду-1) А,у ' Уб " Ал ^— Ду)

ДуД .

А,у ' ( ^n ’ Ал' ^— Ду) Ai" (^i ’ Ai ^— Д)

Решая данную систему, определим Дгасч/ расчетные интенсивности поступления вызовов, поступающих на каждый i-ый ЦОВ. Далее определим величины коррекций интенсивностей потоков вызовов для каждого i-го ЦОВ следующим образом: АА^ Ai Арасчг-. Если полученное значение АЛ отрицательное, то на i-ый ЦОВ необходимо перемаршрутизировать дополнительный поток заявок с интенсивностью Ml от всех других ЦОВ, если значение положительное – то необходимо перемаршрутизировать избыточный поток заявок с интенсивностью АЛ от i-го ЦОВ ко всем другим ЦОВ. Распределять дополнительную нагрузку АЛ между ЦОВ можно по различным критериям (например, по наименьшему расстоянию между парой ЦОВ).

Рассмотрим данный алгоритм на конкретном примере при следующих исходных данных.

• 1.    В составе РЦОВ имеется четыре ЦОВ.

• 2.    Число операторов в каждом ЦОВ: N ₁ = 5; N ₂ = 4; N ₃ = 6; N ₄ = 10.

• 3.    Производительность одного оператора i -го ЦОВ (выз/ч); //1 = 20, //₂ = 15, рз = 30, //4=24.

• 4.    Интенсивность поступления вызовов в i -ый ЦОВ (выз/ч): Л = 25, Л =15, Л = 20, л =18.

Найдем неизвестные расчетные интенсивности входящих потоков вызовов на каждый i -ый ЦОВ ^расч/> , решив систему уравнений (4).

Определим также длительности ожидания вызовов в отдельных ЦОВ без перемаршрутизации на основании (2). В случае перемаршрутизации вызовов между различными ЦОВ при их равномерной загрузке среднее время ожидания любого вызова в очереди в РЦОВ будет равно: т = 0,00476 ч = 17,14 с. Результаты численных расчетов сведены в таблицу 1:

Таблица 1. Результаты численных расчетов

Номер ЦОВ	1	2	3	4
2„ выз/час	25	15	20	18
Ярасч,, выз/час	8	4	23	24
|А2,-|, выз/час	17	11	3	6
Тож) , час	0,0167	0,0222	0,0042	0,0034
Т      , час ож.ср.	0,0048

Сравним качество обслуживания нагрузки в РЦОВ при наличии и отсутствии перемаршрутизации вызовов между центрами. Для этого определим долю вызовов, которые будут ожидать обслуживания больше среднего времени ожидания при условии перемаршрутизации вызовов и равной 17,14 с. Долю трафика, поступающего в i-ый ЦОВ, от всей нагрузки на РЦОВ определим по формуле

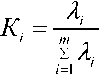
откуда К ₁ = 0,320; К ₂ = 0,192; К ₃ = 0,256; К ₄ = 0,230. С учетом выполненных расчетов видно, что в первом и втором ЦОВ время ожидания вызовов больше среднего времени ожидания по всему РЦОВ, и доля таких вызовов составляет 32% и 19% соответственно. Таким образом, без использования перемаршрутизации почти половина всех вызовов РЦОВ будет обслуживаться с качеством худшим, чем в случае равномерного распределения нагрузки между локальными центрами.

Заключение

Для качественной работы распределенного центра обслуживания вызовов необходимо обеспечить оптимальное распределение поступающей нагрузки за счет ее перемаршрутизации между отдельными локальными центрами. В статье предложен метод равномерного распределения поступающей нагрузки в РЦОВ по всем центрам, основанный на минимизации среднего времени ожидания обслуживания вызовов в очередях. В рассмотренной модели условием выполнения перемаршрутизации вызовов в локальных цен- трах служила оценка превышения времени ожидания в очереди относительно времени ожидания, усредненному по всем центрам РЦОВ.

Однако возможно использование и более сложных условий перемаршрутизации, например задание некоторой границы качества обслуживания в виде правила « Х % вызовов в РЦОВ должно быть обслужено со временем ожидания не более Y с екунд». Реализация такого правила потребует обмена служебной информацией между локальными центрами об их загруженности. Исследование такой модели РЦОВ требует применения более сложных математических моделей и методов анализа.