Анализ граничных задержек в сети TSN Ethernet

Традиционные интернет-сети, которые обеспечивают сквозное соединение для пользователей, успешно сокращают операционные сквозные задержки только до десятков миллисекунд. Однако нынешние и будущие приложения требуют сверхнизкие или граничные задержки ULL (Ultra Low Latency) [1]. Критически важны задержки в медицинских приложениях для телехирургии и транспорта, так как требуют подключения к сети почти в реальном времени. Требования к пропускной способности в значительной степени зависят от потребностей приложений, которые могут широко варьироваться от небольших объемов данных интернет вещей IoT (Internet of Things) до крупных обменов мультимедийными данными, передаваемыми в облако и из облака [2].

Тематика исследования граничных задержек в сетях, чувствительных ко времени TSN (Time Sensitive Networking) Ethernet, заключается в том, что в таких разнородных средах, как автомобильные транспортные средства, дополненная и виртуальная реальность AR/VR (Augmented reality/ Virtual Reality), а также роботизированные приложения, которые необходимы для промышленного интернета вещей IIoT (Industrial Internet od Things), могут потребоваться как высокие скорости передачи данных, так и ULL [3]. Высокие скорости передачи данных могут потребоваться для передачи видеопотока с камер, которые используются для управления транспортными средствами и роботами, а в приложениях будет очень полезен специальный механизм для универсального удовлетворения разнообразных требований ULL.

Исходя из вышеперечисленных аспектов, можно сделать вывод, что данное исследование имеет актуальность [4].

Технология TSN Ethernet

Представим сеть TSN в виде графа, состоящего из набора узлов, которые могут быть либо конечными системами (ES), либо коммутаторами (SW), подключенными через физические каналы. Предполагается, что каналы являются полнодуплексными, что позволяет осуществлять связь в обоих направлениях. Пример проиллюстрирован на рисунке 1, где есть 4 конечных системы, от ES1 до ES4, и 3 переключателя, от SW1 до SW3.

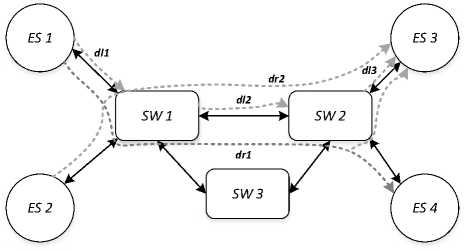
Рисунок 1. Пример топологии сети TSN

Топология сети TSN моделируется как неориентированный граф, где V = ES U SW — это набор конечных систем ( ES ) и коммутаторов ( SW ), а E – набор физических каналов. Для рисунка 1

V = ES U { ES 1; ES 2; ES 3; ES 4} U { SW 1; SW 2; SW 3} , а физические ссылки показаны двойными черными стрелками. Связь с потоком данных dl_i = [ v_a ; v_b ] ∈ L , где L – это набор каналов передачи данных в сети, является направленным ребром от v_a к v_b , где v_a и v_b ∈ V могут быть ESes или SWs . Скорость физического канала обозначается как dl_k * C . Предположим то, что все физические ссылки имеют одинаковую скорость C . Поскольку существует только один выходной порт для каждой ссылки потока данных, dl_k также может ссылаться на выходной порт h в v_a , связанный со ссылкой на v_b . Маршрутизация потока данных dr_k ∈ R представляет собой упорядоченную последовательность каналов потока данных, соединяющих единственную исходную ES с одной или несколькими ES назначения. Например, на рисунке 1 dr1 соединяет исходную оконечную систему ES1 с оконечными системами назначения ES3 и ES4, а dr2 соединяет ES2 с ES3.

Задачи приложений, работающих в ESes, обмениваются данными через потоки, которые имеют один источник и могут иметь несколько пунктов назначения. Несмотря на то, что в сети может быть некритическая связь, рассмотрим критические потоки, которые имеют требования в реальном времени. Определим т = UkTTTk как множество всех критических потоков в сети TSN [5].

Как уже упоминалось, стандарт TSN поддерживает разные приоритеты для критических потоков TT (Time-Triggered). Предполагается, что приоритет P_m при m ∈ [1;8] для каждого критического потока TT был определен разработчиком системы. Более того, для каждого потока TT τ _TTk ∈ τ , известен размер кадра l_TTk , период p_TTk в исходной ES и статически определенную маршрутизацию dr_TTk .

Оценка наихудшего случая передаваемых в сети задержек и задержек потоков производится путем внедрения теории сетевого исчисления, которая, в свою очередь, разработана для детерминированного анализа производительности сетевой связи. Операция свертки min-plus алгебры (min;+) определяет кривые поступления и обслуживания, которые для проведения анализа осуществляют их построение, а также описывает доступность сетевых узлов и поведение потоков.

R ( t ) – это подсчитанное общее, входящее в сеть до момента t , количество битов, представляющее совокупность функции ввода потока, которые моделируют процесс поступления с помощью кривой поступления α ( t ). Только при:

R(t) ≤inf{R(s)}+α(t - s)} =(R ⊗α)(t), 0≤s≤t где R(s) – функция потока;

α ( t ) – кривая поступления, которая описывает границу потока R ( s );

( t - s ) – любой период, на интервале от 0 до t , в течение которого α ( t ) будет кривой поступления для потока R ( s );

⊗ – операция свертки min-plus;

inf – выражает infimum, т.е. точную нижнюю границу.

Примером кривой поступления является модель маркерной корзины, описываемая максимальным скачок потока (σ) и верхней границей долгосрочной средней скорости потока (ρ) [6].

Кривая обслуживания β ( t ) моделирует обрабатывающую способность доступного ресурса. Пусть, подсчитывает общее количество битов потока, выходящего из сетевого узла до момента времени t , процесс отправления R ^*( t ), представляющий кумулятивную, т.е. накапливающую функцию выхода. Сетевой узел предлагает кривую обслуживания β ( t ) для потока, если:

R(t) ≤inf{R(s)}+ β(t - s)} =(R ⊗ β)(t), 0≤s≤t где R(s) – функция потока;

β ( t ) – кривая обслуживания, которая описывает границу потока R ( s );

( t - s ) – любой период, на интервале от 0 до t, в течение которого β ( t ) будет кривой обслуживания для потока R ( s );

⊗ – операция свертки min-plus;

inf – выражает infimum, т.е. точную нижнюю границу.

Типичным примером кривой обслуживания является кривая обслуживания «скорость-задержка» вида:

βR,T(t)=R[t-T]+, где R – скорость обслуживания;

t – момент времени;

T – задержка обслуживания;

[ x ] ⁺ – равна x , если x ≥ 0, и 0 в противном случае.

Задержка, которую испытывает поток в сетевом узле, будет ограничена между графиками двух кривых, тогда максимальное горизонтальное отклонение будет:

h ( α , β ) = sup{inf{ τ ≥ 0 | α ( s ) ≤ β ( s + τ )}} , где sup – точна верхняя граница или супремум;

inf – выражает infimum, т.е. точную нижнюю границу;

α ( t ) – кривая поступления, которая ограничивает поток R ( s );

β ( t ) – кривая обслуживания, которая описывает границу потока R ( s ).

Проанализируем ограниченный маркерной корзиной поток α_{σ , ρ} ( t ) и кривую обслуживания скорость/время ожидания, в узле β _{R , T} ( t ) [5].

Наихудшая задержка проиллюстрирована с помощью двойной серой стрелки, обозначенной буквой h ( α ; β ) на рисунке 2.

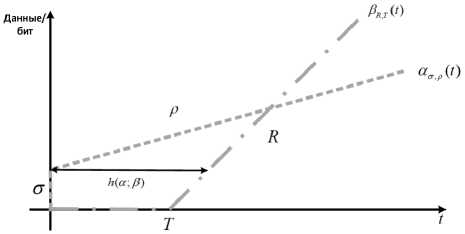
Рисунок 2. Основная схема снятия

Наихудшая сквозная задержка потока представляет собой сумму пределов задержки в сетевых узлах вдоль его маршрутизированного пути виртуального канала [7].

Важно получить суммарную кривую поступления, для потоков, которые конкурируют на выходном порту, а также предоставленную устройством кривую обслуживания, чтобы получить для критического потока в узле входного порта задержку. По маршрутизированному пути распространяются границы задержки, из чего и получается для критического потока наихудшая сквозная задержка WCD (Worst-Case end-to-end Delay).

Существует с разными уровнями приоритета P_m (1 ≤ m ≤ n ) для критического трафика n (1 ≤ n ≤ 8) очередей. В свою очередь в те же очереди входят с разными уровнями приоритета критические потоки P_m . Кадры в каждой очереди следуют порядку «первым пришел – первым обслужен» FIFO (First in, First out), и кадры имеют более высокий приоритет в очереди Q_P , чем в очереди Q_P . Пересылка кадров осуществляется тогда, когда связанный со шлюзом G_P , для управляемой GCL очереди Q_P , которая в свою очередь управляется открытыми G_P ( t ) = 1 и закрытыми состояниями G_P ( t ) = 0, шлюз открыт. На рисунке 3 проиллюстрировано открытие и открытие-закрытие шлюза G_P , цикл которого равен T_P , длина же в цикле открытия-закрытия в свою очередь равна L_P .

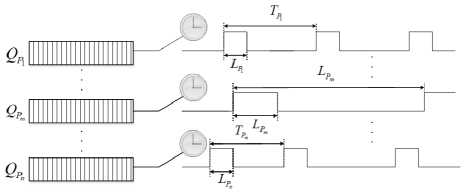
Рисунок 3. Процесс открытия и открытия входа каждой очереди

До момента закрытия шлюза, определяется время отправки всего кадра, которое в свою очередь определяет механизм опережающего просмотра, для каждого класса трафика, утвержденный стандартом 802.1Qbv. Время простоя, т.е. защитная полоса, определяется, когда переадресация кадра до следующего открытого окна не может быть возможна и возникает в конце текущего открытого окна. Максимальный размер передаваемого блока Ethernet MTU (Maximum Transmission Unit) в 1500 байтов в худшем случае больше защитной полосы. Критический кадр, уже находящийся на передаче, не может быть прерван кадром с более высоким приоритетом. Это подразумевает политика не приоритетного прерывания, т. е. отсутствие поддержки IEEE 802.1Qbu, если шлюзы открыты в то же время. Из-за возможного перекрытия с открытыми окнами других важных очередей, служебный ре- сурс, во время открытого окна QP для трафика Pm может быть не выделен [8].

Взаимоисключающей и специализированной для каждого класса трафика является услуга TDMA (Time Division Multiple Access), которая отличается от службы в одном узле для критического трафика с P_m . Из этого следует то, что повторяется, с фиксированной длиной цикла, временной интервал TDMA для трафика с нижней границей, т.е. гарантированной услугой. Но, как можно предположить, может возникнуть перекрытие, и для трафика P_m не будет выделен временной интервал обслуживания, управляемый GCL (Gate Control List) в TSN.

Необходимо получить длительность L_P временного интервала, для гарантированного обслуживания в каждом открытом окне Q_P от P_m , чтобы получить кривую обслуживания для трафика P_m . На рисунке 4 проиллюстрирована связь максимальной защитной полосы перед каждым открытым окном Q_P , которая зависит не только от наихудшего перекрытия критического трафика с более высоким и низким приоритетом.

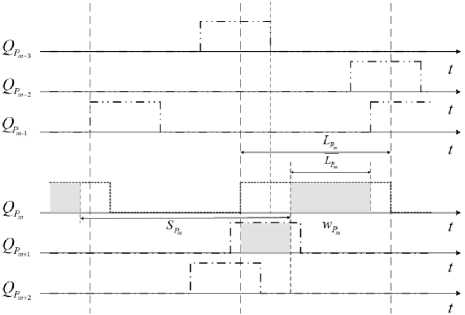
Рисунок 4. Гарантированный временной интервал в открытом окне

Первый кадр периода ожидания P_m получает услугу из соответствующего временного интервала что является максимальным временем ожидания S_P , которое в свою очередь связано с наихудшим перекрытием с другим приоритетным трафиком и максимальным размером кадра в Q_P .

Из-за различных ситуаций перекрытия с очередями с более высоким и более низ ки м приоритетом, длина временного интервала L_P гарантированного обслуживания является переменной в разных открытых окнах Q_P , что и отмечено на

12  3

рисунке 5 как L_P , L_P и L_P

.

Первый кадр периода ожидания Pm получает услугу из соответствующего временного интервала что является максимальным временем ожидания S , которое в свою очередь связано с наихудшим Pm перекрытием с другим приоритетным трафиком и максимальным размером кадра в QP [9].

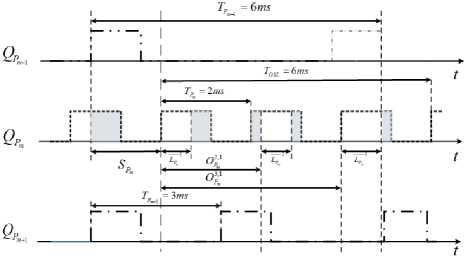
Рисунок 5. Гарантированный временной интервал в открытом окне

Из-за различных ситуаций перекрытия с очередями с более высоким и более низким приори- тетом, длина временного интервала LP гарантированного обслуживания является переменной в разных открытых окнах QP , что и отмечено на рис. 6 как L 1 , Pm

L и L mm

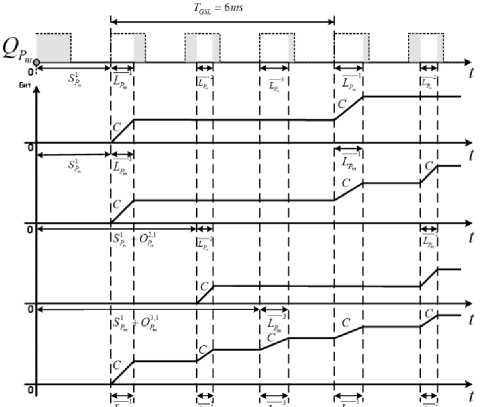
Рисунок 6. Гарантированные временные интервалы для P_m

Стоит обратить внимание на то, что наименьшим общим кратным LCM (Least Common Multiple) циклов открытия-закрытия T_P (1 ≤ m ≤ n ) для всех очередей приоритета критического трафика, является GCL выходной порт, перекрывающийся отношением повторяющегося гиперпериода T_GCL . Для гарантированного временного интервала трафика P_m , существует ограничение количества случаев длины L_P , которое обозначается как N_P . Например, N_P равно 3, когда T_{P -} = 6 мс, T_P = 2 мс, T_{P +} = 3 мс и, следовательно, гиперпериод T_GCL = 6 на рисунок 6 [10].

Гарантированное обслуживание для Pm, трафика теряет периодичность TP . Чтобы представить взаимное расположение соседнего гарантиро- ванного временного интервала, определим относительное смещение стр^1 (j е [i +1, i + N^ -1]), которое представляет собой временной интервал между временем начала i-го и j-го гарантированных временных интервалов для Pm трафика, если принять i-й гарантированный временной интервал в качестве эталона. Например, на рисунке 6, стр’1 и стр1 соответственно представляют относительные m        12          1

смещения между L и L , а также между L Pm      Pm                         Pm и LP , принимая гарантированное окно обслуживания с длиной L 1 в качестве эталона. Обратите Pm внимание, что стр, равно 0, если j = i.

Теорема 1: возможная кривая обслуживания вРт (t) для критического трафика приоритета Pm с учетом гарантированного временного интервала LiPm (i = 1;…; NP) в качестве эталона определяется формулой (5) и (6):

не может быть гарантирован для P_m – трафика, в то время, как обслуживание ^C *^{( A- (} S P_m + ^CT p m i + ^{( 9} + 1) * ^T gcl )) в любом временном интервале

S P m + ст Р, + ( 9 + 1)* T gcl

< SPm + CTP^ + (9 + 1)* TGCL + LPm , может быть гарантирована для трафика Pm. Для последовательности периодических временных интервалов с длиной LP , кривая обслуживания задается как:

A i;i ( t ) = в -j ( t + T gcl - L^ j - SP> - ct;^ i ) , m             m   mm

GCL,L , Pm где Ptgcl,L^1 (t) - классическая кривая обслуживания TDMA;

S P^ - ст р , i — относительное смещение от времени начала t₀ периода до времени н ач ала гарантированного временного интервала L_P [7].

i + N_P - 1

P _m

А ( t ) = E j • ) .

j = ¹

где

j вР, (t) = A    j (t + Tgcl - L Pm - Sp„ - стр ), m      GCL ,LPm                 mm в L - классическая кривая обслуживания моделей изменяющегося потока в сочетании с про-

токолом TDMA [11].

в _{т L} ( t ) = C * max(

t

T

L , t -

( T - L )) .

Доказательство: принятие гарантированного временного интервала Lⁱ P m в качестве эталона означает, что первый кадр периода отставания P_m

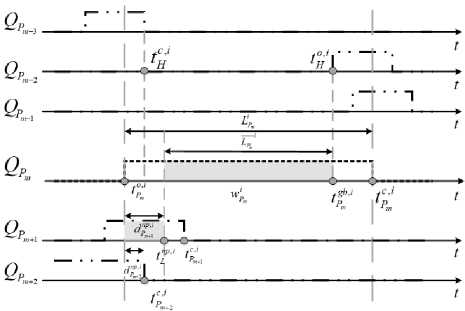
Рисунок 7. Граничный вид обслуживания на основе эталонного теста

получит услугу, начиная с временного интервала LiPm. Затем отдельно рассматривается NP – последовательности периодических гарантированных временных интервалов, которые отдельно повторяются в соответствии с гиперпериодом TGCL, чтобы получить кривую обслуживания, например, на рисунке 7.

Обслуживание трафика Pm не может быть га- рантировано ни в каком временном интервале

0 t - t ₀ <  S P _m + ст р , ¹ , тогда для периодической последовательност и в ременных интервалов обслуживания длина равна L_P^j ( i <  j <  i + N_P - 1 . В любом временном интервале S P + ст р , ¹ < A <  S p + ст р , ¹ + L p_m , можно гарантировать обслуживание C *( A - S p - CTP, ■ ¹ )

Кроме того, пос кол ьку гарантированный временной интервал L_P повторяется с T_GCL , услуга в течение любого временного интервала

S i + ст pi + 9

mm .

T gcl + L j < A| <  S ^ + CT j + ( 9 + 1)* T gcl ( 9 N )

В качестве эталона из суммы кривых обслуживания каждой периодической последовательнос ти , состоящей из временных интервалов длиной L_P j ( i <  j < i + N_P - 1) как показано, например, на рисунке 6.

Получается возможная кривая обслуживания для трафика P_m с использов ани ем гарантированного временного интервала L_Pⁱ , что и проиллюстрировано на рисунке 6.

До сих пор были выведены возможные кривые N_р , обслуживания A _P ( t ) ( i = 1; • - ; N р ) для трафика P_m , рассмотренные различными гарантированными временными интервалами в гиперпериоде в качестве эталонов. Тогда кривая обслуживания в _Р ( _t ) для трафика P_m является наихудшим случаем из всех возможных кривых обслуживания, то есть нижней огибающей PP_m ( t ):

A ( t ) = min {Ap ( t )}

P^m         1 < i <  N      P m       ,

Pm где ePm (t) – кривая обслуживания для трафика Pm .

Заключение

Что бы рассмотреть проблему анализа граничных задержек в сетях TSN, была построена прикладная модель сети TSN в виде графа и осуществлен детерминированный анализ сети. В данном анализе была представлена модель сети TSN Ethernet на базе теории сетевого исчисления, в которой была произведена оценка наихудшего случая передаваемых в сети задержек и задержек потоков. Для получения суммарной кривой поступления, для потоков, конкурентов на выходном порту, была применена оценка критического трафика.