Анализ и классификация многокритериальных методов принятия решений

Процесс принятия решений (ПР) всегда связан с оценкой большого количества факторов и рассмотрения возможных альтернатив, поэтому его можно определить как сложный интеллектуальный процесс, целью которого является выбор оптимального решения на основе различных критериев, определяемых лицом, принимающим решение (ЛПР). Основной сложностью в выборе одной из альтернатив является то, что критерии оценки зачастую конфликтуют между собой, что в большинстве случаев делает невозможным выбор решения, превосходящего все остальные по каждому из критериев [1]. Поэтому для ПР ЛПР используют один или комбинацию из нескольких многокритеральных методов ПР (ММПР).

ММПР разрабатывались в трудах отечественных и зарубежных авторов в различных областях. Например, среди отечественных исследователей можно отметить: решение многокритериальных задач линейного программирования (академик С.В. Емельянов [2]); задачи

• 1    Редакция вновь даёт дорогу молодым авторам, которые смело берутся за обзорные статьи. Во втором номере журнала за этот год был опубликован обзор подходов к автоматизации работ с онтологическими ресурсами, подготовленный молодым научным сотрудником М.А. Шишенковым. Представляемый на суд читателям обзор по методам принятия решений со многими критериями призван повысить эффективность принимаемых решений. Редакция ожидает получить обратную связь от читателей и новые работы в этой области с той же целью, которую для себя обозначил молодой автор. Прим. ред.

оптимального управления (академик Н.Н. Моисеев [3]); многокритериальную оптимизацию с ранжированием критериев по важности (профессор Е.С. Вентцель [4]); ММПР при конструировании машин и механизмов (И.М. Соболь и Р.Б. Статников [5]); методы свёртки критериев в многокритериальных задачах оптимизации (профессор Ю.Б. Гермейер [6]); методы сравнения важности неоднородных критериев и групп критериев (профессор В.В. Подиновский [7]) и др. По данным научной электронной библиотеки elibrary.ru , а также публикациям [8, 9] в последние годы наблюдается рост статей по ММПР.

Целью данного исследования является систематизация ММПР и разработка их классификации, которая могла бы повысить эффективность выбора ММПР при создании специализированного программного обеспечения (ПО) для систем поддержки ПР (СППР). Для достижения цели необходимо провести анализ существующих ММПР, их основных классификаций и выявить ключевые ограничения ММПР.

1    Основные ММПР 1.1    Определение области исследования

Опыт по созданию ММПР позволил накопить большой объём различных моделей, подходов и целых семейств методов [8]. Известно более 200 ММПР и их количество продолжает расти [9, 10]. Целесообразным является рассмотрение наиболее распространённых на практике ММПР, где измеряемым показателем распространённости принято число научных работ о методе (см. таблицы 1 и 2).

Таблица 1 - Наиболее часто используемые многокритеральные методы принятия решений (согласно [8])

Оригинальное название метода	Перевод	Количество научных статей с методом
Fuzzy sets [11]	Нечёткие множества	1471
Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [12]	Метод порядка предпочтения по сходству с идеальным решением	939
Analytic Network Process (ANP) [13]	Метод анализа сетей	281
Decision Making Trial and Evaluation Laboratory (DEMATEL) [ 14]	Лаборатория испытаний и оценки ПР	227
Best-Worst Method (BWM) [15]	Метод лучшего-худшего	174
Visekriterijumska Kompromisno Rangiranje (VIKOR) [16]	Компромиссный рейтинг по многим критериям	168
Fuzzy AHP [17]	Нечёткий метод анализа иерархий	162
Fuzzy TOPSIS [18]	Нечёткий метод порядка предпочтения по сходству с идеальным решением	162
ENTROPY [19]	Энтропия	122
Grey Relational Analysis (GRA) [20]	Серый реляционный анализ	106

Данные, представленные в таблице 1, являются результатом анализа баз данных (БД) Web of Science и EBSCO Discovery Service engine c 2018 по 2023 гг. Из таблицы 1 видно, что преобладают Fuzzy -методы и метод TOPSIS .

Для оценки распространённости методов в научном дискурсе использовались показатели общего количества работ в БД « ScienceDirect » в период с 2012 по 2022 гг. (см. таблицу 2).

Основные ММПР, представленные в научных публикациях по степени их практического использования, приведены в таблице 3.

Исходя из представленных результатов исследований [8, 9, 38], можно ограничить круг рассматриваемых ММПР следующими методами: SAW , MAUT , MAVT , SMART , AHP , ANP , BWM , TOPSIS , VIKOR , CBR , DEA , ELECTRE , PROMETHEE , Fuzzy -методами и GRA .

Таблица 2 – Наиболее часто используемые многокритеральные методы принятия решений (согласно [9])

Оригинальное название	Перевод	Количество научных статей с методом
Analytic Hierarchy Process (AHP) [21]	Метод анализа иерархий	15452
Data Envelopment Analysis (DEA) [22]	Анализ охвата данных	9367
Fuzzy sets [11]	Нечёткие множества	8730
TOPSIS [12]	Метод порядка предпочтения по сходству с идеальным решением	8241
Case-Based Reasoning (CBR) [23]	На основе прецедентов	3258
GRA / Grey Relational Model (GRM) [20]	Серый реляционный анализ / Серая реляционная модель	3176
ANP [13]	Метод анализа сетей	3126
Fuzzy AHP [17]	Нечёткий метод анализа иерархий	2804
ÉLimination Et Choix Traduisant la REalité (ELECTRE) [24]	Исключение и выбор, преобразующий реальность	2782
Preference Ranking Organization METHod for Enrichment of Evaluations (PROMETHEE) [25]	Метод организации ранжирования предпочтений для обогащения оценок	2715
VIKOR [16]	Компромиссный рейтинг по многим критериям	2691
Fuzzy TOPSIS [18]	Нечёткий метод порядка предпочтения по сходству с идеальным решением	2014
DEMATEL [14]	Лаборатория испытаний и оценки ПР	1378
Preference Ranking Global frequencies in Multicriterion Analysis (PRAGMA) [26]	Ранжирование глобальных частот в многокритериальном анализе	1267
Simple Additive Weighting (SAW) [27]	Простое аддитивное взвешивание	976
Multi-Attribute Utility Theory (MAUT) [28]	Многокритериальная теории полезности	948
BWM [15]	Метод лучшего-худшего	867
Simple Multi-Attribute Rating Technique (SMART) [29]	Простая методика многокритериальной оценки	646
Fuzzy ANP [30]	Нечёткий метод анализа сетей	586
Weighted Sum Model (WSM) [31]	Модель взвешенной суммы	470
COmplex PRoportional ASsessment (COPRAS) [32]	Комплексная пропорциональная оценка	445
Multiple-Attribute Value Theory (MAVT) [33]	Многокритериальная теория ценности	315
Dominance-based Rough Set Approach (DRSA) [34]	Подход грубого набора, основанный на доминировании	278
Weighted Aggregated Sum Product ASsessment (WASPAS) [35]	Оценка результата взвешенной агрегированной суммы	270
Weighted Product Model (WPM) [36]	Модель взвешенных результатов	198
Measuring Attractiveness by a CategoricalBased Evaluation TecHnique (MACBETH) [37]	Измерение предпочтительности с помощью категориального метода оценки	162

1.2 Анализ ММПР Среди ММПР, представленных в таблице 2, первым был разработан метод SAW. Несмотря на относительно малое количество упоминаний в научных исследованиях последних лет, SAW Таблица 3 – Частота практического применения многокритеральных методов принятия решений (согласно [38]) Метод Описанные случаи практического использования AHP, fuzzy AHP, трапециевидный fuzzy AHP и ANP 70 TOPSIS, fuzzy TOPSIS и модификации TOPSIS 22 SAW 21 Целевое программирование 10 ELECTRE 7 MAUT и MAVT 7 PROMETHEE 5 VIKOR и fuzzy VIKOR 3 Прочие 20 является одним из самых востребованных ММПР (см. таблицу 3). Это обусловлено простым алгоритмом расчёта, который можно реализовать без использования специализированных компьютерных инструментов [38]. Основой идеей метода является объединение значений и весов критериев в единый критерий. SAW обладает характерными для многих ММПР недостатками: невозможно использовать качественные данные без их перевода в количественные, необходимо наличие заранее известных данных, в т.ч. и весов критериев [39, 40].

Развитие SAW получил в методах MAUT , MAVT и SMART . Эти методы связаны друг с другом, т.к. MAUT расширяет MAVT , а SMART разработан, чтобы обеспечить простой способ реализации метода MAUT [41, 42]. Данная группа методов помогает определить наилучшую альтернативу, назначая полезность каждому возможному последствию и вычисляя наилучшую возможную полезность. Метод MAVT стал основой данного направления в ММПР. Процедура помощи при ПР, предлагаемая MAVT , заключается в выстраивании альтернатив, сравнении их по общему набору критериев, присвоении баллов каждой альтернативе в соответствии с её эффективностью по каждому критерию, взвешивании этих критериев и расчёте общего балла для каждой альтернативы [43]. Ключевым элементом MAVT является концепция уровней предпочтений [44]. Основными недостатками MAVT являются: полная компенсация критериев и возникающая потребность в концептуальном усложнении при попытках формально определить значение оценок и весов [43, 44].

Метод MAUT привнёс нововведение в основную идею MAVT . Его главное преимущество – способность учитывать неопределённость, поэтому MAUT нашёл широкое применение в экономике, финансах, управлении водными ресурсами и др. сферах, содержащих значительную степень неопределённости и достаточное количество доступных данных [41]. Среди преимуществ метода MAUT можно выделить следующие: ■ учёт последствий на каждом этапе [39];

• ■    возможность оценки вновь появляющихся альтернатив [40];

• ■    возможность проведения анализа большого количества альтернатив [45].

В развитие метода MAUT появился SMART – одна из простейших его форм, которая преобразует веса важности в фактические числа [38]. В последствии были созданы методы SMARTS и SMARTER [42]. Основные преимущества SMART в том, что он прост в использовании, допускает любые методы присвоения весов, что требует меньших усилий со стороны ЛПР, чем MAUT , и SMART хорошо обрабатывает данные по каждому критерию [38]. Метод чувствителен к большому количеству критериев и учёту диапазонов шкал при определении весов критериев [40, 42].

Самая востребованная группа методов (см. таблицы 2, 3) – AHP и ANP . AHP – позволяет принимать сложные решения, разделяя их на иерархические уровни. Его можно использовать для определения относительной важности различных критериев при ПР или для определения того, какой из нескольких вариантов является наилучшим выбором. В AHP используется попарное сравнение критериев для определения их относительной важности и объединение оценки для ПР [46]. Среди достоинств метода выделяются [39]:

• ■    иерархическая структура проблем ПР;

• ■    возможность объединения результатов от нескольких экспертов;

• ■    возможность оценивать количественные и качественные показатели.

ANP является развитием метода AHP , поэтому унаследовал от него большую часть достоинств и недостатков. ANP не требует строгих иерархических отношений, позволяет рассматривать взаимосвязанные критерии и расставлять приоритеты для групп или кластеров элементов [38]. Среди общих для обоих методов ограничений выделяют то, что коэффициент согласованности допускает противоречивые суждения в матрицах сравнения [39].

Среди методов, использующих попарное сравнение, можно выделить – BWM. В BWM ЛПР определяет лучший и худший критерии с последующим проведением попарных сравнений между каждым из этих критериев [15]. Эти наборы попарных сравнений используются в качестве входных данных для задачи оптимизации, результатами которой являются веса критериев (альтернатив) [15]. В BWM используется меньше сравнений, чем в AHP за счёт отсут- ствия попарного сравнения альтернатив по всем критериям, что делает его более надёжным, согласованным и простым в реализации [47]. Возможность оценивать количественные и качественные показатели является важным преимуществом данного метода. BWM подходит для индивидуального и группового ПР. Базовый BWM включает нелинейную модель, которая иногда приводит к нескольким оптимальным весам, где вес каждого критерия представлен в виде интервала [48].

Наравне с AHP и ANP востребованным ММПР является метод TOPSIS (см. таблицы 1-3). Основной принцип работы TOPSIS заключается в измерении сходства альтернатив с идеальным решением, удалённости от худшего решения и последующем ранжировании с учётом весов используемых критериев [49]. Метод прост в использовании и программной реализации, а количество шагов остаётся неизменным независимо от числа атрибутов [38]. Результаты, получаемые данным методом, остаются устойчивыми при добавлении новых альтернатив, а входные данные не требуется преобразовывать перед использованием [39]. Отмечаются следующие слабые стороны метода TOPSIS [50]:

• ■    требуется независимость критериев, которую трудно гарантировать;

• ■    может приводить к предвзятому ранжированию;

• ■    могут возникать ситуации, когда не существует альтернативы, одновременно удалённой от отрицательного и близкой к положительному идеальному решению.

Метод VIKOR, как и метод TOPSIS , основан на агрегирующей функции, где степень нелинейности задаётся параметром [51]. В данном методе наилучшая альтернатива называется компромиссной и определяется по степени близости к идеальному [52]. Метод VIKOR подходит в случаях, когда ЛПР не имеет предпочтений в решении или не может выразить свои предпочтения на начальных этапах процесса ПР. Отмечаются следующие преимущества VIKOR [39]:

• ■    способность принимать компромиссные решения, решения с максимальной групповой полезностью и минимальным индивидуальным сожалением;

• ■    оценивание веса, которое позволяет проанализировать конечное компромиссное решение;

• ■    компромиссное решение может быть заменено, если мера веса не укладывается в интервал.

Для работы VIKOR необходимо назначение весов критериев и конвертация качественных данных в количественные [39].

Среди рассматриваемых ММПР метод CBR используется для извлечения новых знаний из уже имеющихся данных [53]. Для работы CBR необходимо большое количество данных о различных ситуациях в прошлом, что является существенным ограничением для работы в инновационных проектах.

Методология DEA позволяет оценивать границу эффективности путём сравнения альтернатив с наилучшей производительностью с использованием методов математического программирования [54]. Концепция эффективности в DEA определяется как отношение полученных результатов к используемым ресурсам [55]. Данный подход позволяет выявить скрытые связи, а также включать в процесс ПР новые альтернативы без изменения порядка ранжирования [38]. DEA не подходит для ситуаций, когда невозможно получить точные данные по альтернативам, а также имеет ограничение по количеству альтернатив и критериев [39].

Иной подход к организации процесса ПР базируется на теории отношения превосходства. Известными представителями таких ММПР являются ELECTRE и PROMETHEE .

ELECTRE – методы, которые развиваются с 60-х годов прошлого века, и известны в нескольких вариантах [56]. Все варианты метода ELECTRE имеют схожий принцип работы, но различаются по типам решаемых задач. Схема работы метода ELECTRE состоит в сравнении каждой пары альтернатив и обнаружении доминирующей и не доминирующей альтернативы. Из принципа работы следует наличие лишь относительной оценки альтернатив, а не абсолютной. Среди преимуществ данного семейства методов выделяют [40, 56-58]:

• ■    быстроту процедуры решения задач;

• ■    введение понятия «несравнимости альтернатив»;

• ■    наличие встроенного инструмента анализа для ЛПР и поэтапность выявления предпочтений ЛПР.

К ограничениям метода относятся [40, 56-58]:

• ■    использование пороговых значений, которые могут быть произвольными, но при этом способны оказывать существенное влияние на окончательное решение;

• ■    неспособность обрабатывать порядковые шкалы;

• ■    удаление или добавление альтернативы может изменить ранжирование между остальными;

• ■    необходимо наличие заранее известных весов критериев.

PROMETHEE - это семейство методов, которые используют несколько итераций для получения рейтинга среди конечного набора альтернатив. Ограничением метода является отсутствие чёткой методики присвоения весов критериям [38]. В случае большого количества критериев могут появиться сложности с оценкой результатов, а при добавлении новой альтернативы необходимо заново проводить анализ [39]. По целям использования выделяются следующие представители PROMETHEE :

• ■    PROMETHEE I - частичное ранжирование;

• ■    PROMETHEE II - полное ранжирование;

• ■    PROMETHEE III - ранжирование на основе интервалов;

• ■    PROMETHEE IV - набор решений для частичного и полного ранжирования;

• ■    PROMETHEE V - проблемы, связанные с ограничениями сегментации;

• ■    PROMETHEE VI - представление человеческого мозга;

• ■    PROMETHEE GDSS - групповое ПР;

• ■    PROMETHEE GAIA - графическое представление.

Важным общим преимуществом таких подходов является отсутствие компенсации между критериями и любых процессов нормализации, изменяющих исходные данные.

Методы ELECTRE и PROMETHEE возможно применить для отбрасывания некоторых неприемлемых альтернатив и впоследствии использовать другой ММПР для выбора наилучшего решения.

Значимым для теории принятия многокритериальных решений является использование понятий нечёткой логики и теории нечётких множеств «Fuzzy set theory » ( FST) [11]. Использование теории нечётких множеств создаёт возможность перехода от бинарных категорий обычной логики к множеству альтернатив среди них. Применение методов FST позволяет [59, 60]:

• ■    использовать нестрогие рассуждения в системах управления;

• ■    принимать решения в условиях неопределённости;

• ■    моделировать приёмы мышления человека.

Многие из рассмотренных ММПР были расширены с помощью FST ( Fuzzy MA UT , Fuzzy AHP , Fuzzy PROMETHEE , Fuzzy MAVT , Fuzzy ELECTRE и т.д.) [61].

Одним из ведущих ММПР в области работы с неполной информацией является метод GRA . Это подход к ПР с частично известной и частично неизвестной информацией в сложных системах со взаимосвязанными критериями [32, 62]. В GRA осуществляется анализ отношений сходства между эталонным значением и альтернативой. Избранный альтернативный ряд, имеющий наиболее близкое сходство с эталоном, является лучшим решением. GRA , в отличие от FST , даёт ЛПР возможность изменения цели в процессе ПР [63]. Одним из типичных недостатков большинства ММПР, способных работать при неполноте информации, является сложность вычислений, что характерно и для GRA . Важным ограничением метода является невозможность использования качественных показателей [64].

Большинство рассматриваемых методов могут давать схожие результаты. Несмотря на разные способы нормализации и агрегации данных, при ранжировании альтернатив с помощью ММПР достигается высокая корреляция Спирмена: 0,949 [65], 0,798 [66], 0,88 [67]. Представленные результаты характерны для статичного набора альтернатив и критериев. При сравнении показателей ранговой корреляции Спирмена показано, что с увеличением ко- личества альтернатив сходство между результатами неизменного набора методов (TOPSIS, SAW, AHP, ELECTRE, VIKOR и т.д.) увеличивается, а с увеличением количества альтернатив - уменьшается [68]. Таким образом, наиболее остро проблема выбора ММПР стоит в ситуации ПР с большим количеством альтернатив и малым набором критериев, т.к. в данном случае наблюдается существенная разница между различными ММПР.

• 1.3 Подходы к решению задачи формализации предпочтений

Исходя из обозначенных в подразделе 1.2 проблем, характерных для большинства ММПР, трудно решаемой задачей является формализация предпочтений ЛПР и определения важности критериев. Можно отметить следующие особенности в этой области:

• ■    ЛПР хорошо понимает условность и неопределённость назначаемых коэффициентов, поскольку ни один человек «не в состоянии облечь свои неформализованные предпочтения в точную числовую форму, и потому не доверяет полученному результату» [69];

• ■    эксперты, специализирующиеся на технических областях, предпочитают выражать свои предпочтения, используя числовые значения, но в случае с представителями социальных наук чаще всего используются слова или лингвистические модели [70];

• ■    при принятии социально значимых решений проблемы с формализацией предпочтений и неопределённостью результатов усиливаются конфликтами ценностей заинтересованных сторон и неопределённостью их реакции на выбор какой-либо альтернативы [71].

Названные особенности обуславливают необходимость предварительной работы с ЛПР с целью выявления, формулирования, конкретизации и анализа их предпочтений. Данная работа может проводиться как в явном, например, через проведение анкетирования или интервью перед использованием методов, для которых необходимо наличие весов критериев, так и в неявном виде, например, в рамках работы с методами, имеющими встроенный механизм оценки критериев ( MACBETH , BWM и т.п.).

В задаче формализации предпочтений ЛПР существует множество подходов, которые могут применяться в зависимости от конкретной ситуации. В связи с тем, что для работы с большинством ММПР требуется наличие определённого перечня альтернатив и критериев и их изначально определённых весов, необходимым элементом процесса формализации является определение важности критериев путём назначения им весов. Выполнить это позволяют в т.ч. следующие методы:

• ■    парного сравнения критериев [72];

• ■    универсальных коэффициентов важности критериев [69];

• ■    базирующиеся на аналитической взаимосвязи показателей предпочтения критериев [73];

• ■    основанные на формальном подходе [73].

• 2.1    Анализ существующих классификаций ММПР

Одна из самых подробных классификаций методов определения коэффициентов важности представлена в работе [74]. В обобщённом формате она представлена на рисунке 1.

2 Классификация ММПР

В теории ПР имеются различные подходы к классификации методов многокритериального выбора, как при конечном, так и при бесконечном множестве альтернатив. Это связано с различными способами определения ключевого различительного критерия и с разработкой новейших ММПР. Например, можно выделить появление методов FST , которые, благодаря развитию математического аппарата, вышли за рамки большинства существовавших классификаций. Из-за роста количества ММПР становится всё сложнее выбрать наиболее подходящий среди них [75].

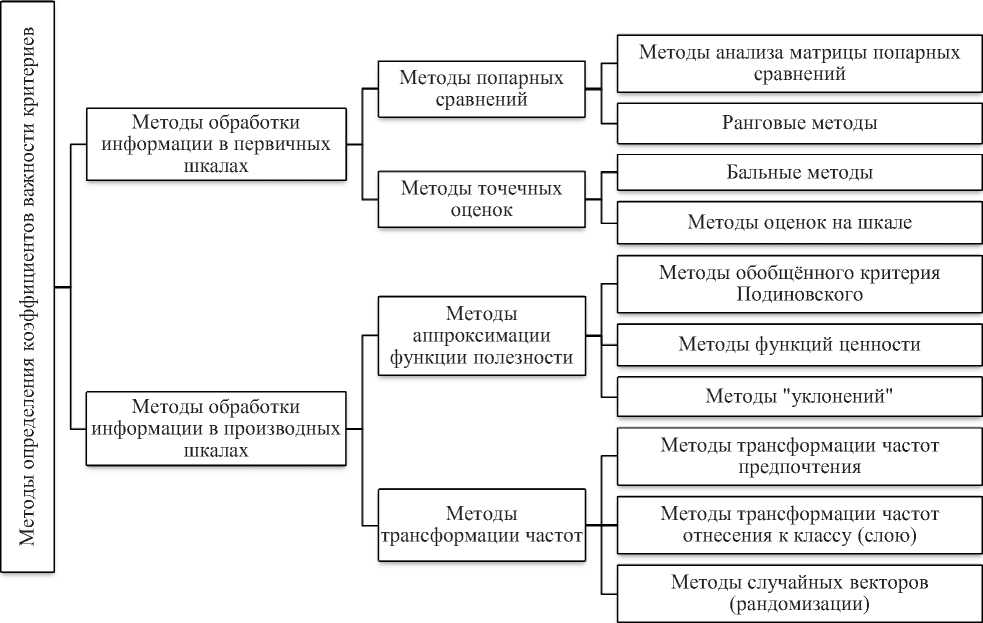
Рисунок 1 - Иерархическая классификация методов определения коэффициентов важности критериев [74]

ММПР можно представить в виде двух категорий [65]:

• ■   MODM ( Multi-Objective Decision-Making ) - многоцелевое ПР - используется для опреде

ления оптимальной альтернативы с учётом ограничений в условиях наличия большого или бесконечного количество альтернативных решений.

• ■    MADM ( Multi-Attribute Decision-Making ) - ПР по множеству атрибутов - используется, когда конечное число предложенных альтернатив оценивается по отношению к различным взвешенным атрибутам для получения рейтинга предпочтений, который описывает эффективность каждой альтернативы для достижения цели в отношении атрибутов.

На основе вышеописанного разделения было создано множество схожих классификаций.

Одна из них представлена на рисунке 2.

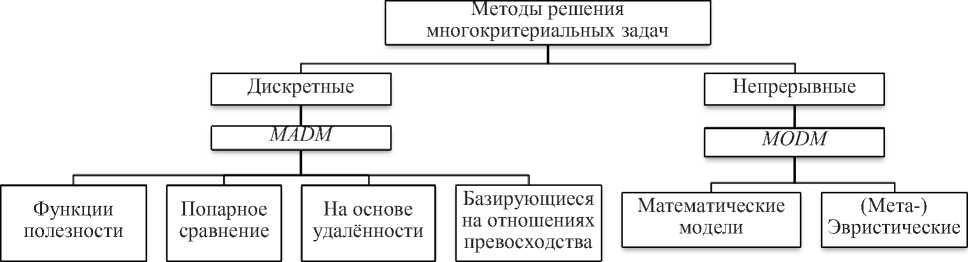
Рисунок 2 - Классификация MADM и MODM методов [76]

Рисунок 2 демонстрирует один из классических подходов к классификации ММПР - разделение на группы, исходя из их принципа анализа альтернатив.

Среди зарубежных классификаций ММПР можно выделить следующие [9]:

• ■    по количеству ЛПР: индивидуальное ПР; групповое ПР.

• ■    по компенсации критериев: компенсаторные; не компенсаторные.

• ■    по отношению к компромиссам: компромиссные подходы; не компромиссные подходы.

• ■    по отношению к типу используемых данных: качественные; количественные.

• ■    по отношению к работе с неопределённостью данных: способные к использованию неопределённых данных; неспособные к использованию неопределённых данных.

• ■    по принципу работы: нефункциональные модели; на основе функциональных моделей; базирующиеся на отношениях превосходства; использующие дискриминантный анализ.

Основным недостатком большинства этих классификаций является отсутствие достаточной информативности при использовании их в СППР. Следует отметить некоторые полезные характеристики для разработки подходящей для СППР классификации – наличие или отсутствие компенсации критериев, типы допустимых для обработки данных, возможность работы с неопределённостью данных.

Среди отечественных классификаций ММПР можно выделить следующие:

• ■    по принципу работы методы [77]: доминантного анализа; многокритериальной оптимизации с ограничениями; многокритериальной оптимизации с взвешенными отклонениями от цели; вычисления приоритетов на основе парных сравнений; многоатрибутной оптимизации по полезности; многокритериальной классификации.

• ■    по основным типам решаемых ими проблем [65]: выбор наилучшего решения из множества; ранжирование и сортировка решений; описание и систематизация решений; описание и систематизация последствий реализации решений.

• 2.2    Разработка классификации ММПР

Самым рассматриваемым видом классификаций являются различные вариации классификаций ММПР по схеме определения наилучшей альтернативы. Данный тип разделения ММПР имеет слабое влияние на выбор того или иного метода как ЛПР, так и программой. При этом использование вышеописанной классификации по наиболее подходящим для них видам задач – важный этап в работе СППР в рамках подбора ММПР, т.к. в первую очередь необходимо подобрать инструмент, способный решать рассматриваемую проблему.

Ещё одной альтернативой представленным выше классификациям по принципу работы может служить классификация, представленная на рисунке 3.

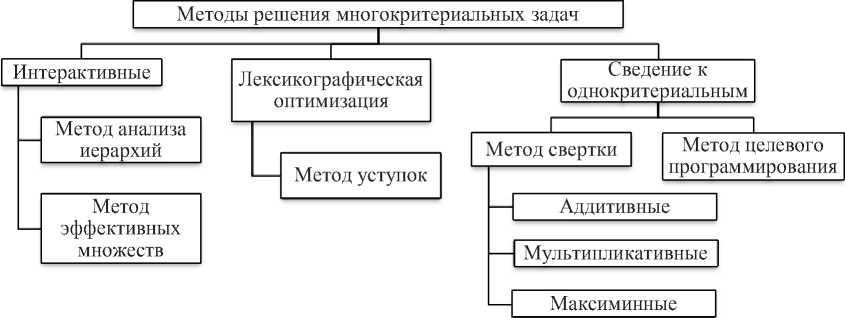
Рисунок 3 – Классификация методов решения многокритериальных задач на основе их принципа работы [78]

Таким образом, анализ имеющихся научных подходов позволяет сделать следующий вывод: существующие классификации достаточно подробно и разносторонне характеризуют ММПР с точки зрения их принципов работы и решаемых ими задач, но в то же время упускают из вида ограничения описываемых ММПР. Такая ситуация не позволяет в полной мере эффективно применять ММПР, т.к. ЛПР и разработчики СППР вынуждены проводить анализ подходящих под их цели ММПР на предмет соответствия этих ММПР требованиям их задачи. Это подтверждает актуальность систематизации основных ММПР с помощью разработки классификации по ограничениям, характерным для данных методов.

В СППР существует несколько основных подходов к определению подходящего ММПР: «система правил», «алгоритм», «искусственная нейронная сеть» [45]. Это обосновано тем, что чаще всего ММПР применяются в группе. Поэтому специализированное ПО включает в себя большое количество не взаимодополняющих ММПР. В большинстве случаев такое ПО применяет «систему правил» (78,3%), смысл которой заключается в нахождении ММПР с помощью набора правил формата «если..., то...» [75].

Исходя из базовой концепции отбора ММПР в СППР, с учётом проведённого анализа существующих методов классификация ММПР должна отражать: разделение методов на их возможности работы с неопределённой информацией; учитывать наличие компенсации критериев; учитывать их зависимость от типов данных, с которыми они работают.

Трансформируя обозначенные ключевые элементы и выявленные в подразделе 1.2 ограничения ММПР в формат «системы правил», можно получить следующие правила, которые необходимо отразить в системе:

• 1.    «Если в текущей задаче присутствуют неизвестные или неточные данные, то необходимо выбрать группу методов, способных работать с неопределённостью»;

  • 1.1.    «Если неточные данные невозможно представить в виде набора дискретных значений, то необходимо выбрать группу методов, работающих с интервальными значениями данных»;

    • 1.1.1.    «Если количество критериев больше семи, то необходимо выбрать группу методов, на которую это не оказывает существенного влияния» ( SMART) ;

    • 1.1.2.  «Если количество критериев меньше семи, то следует выбрать группу методов, чувствитель

ных к количеству критериев» ( MAUT) ;

• 1.2.    «Если неточные данные возможно представить в виде набора дискретных значений, то следует выбрать группу методов, оперирующих дискретными данными»;

  • 1.2.1.    «Если предполагается изменение цели в рамках процесса ПР, то необходимо выбрать группу методов с возможностью изменения целей» ( GRA );

  • 1.2.2.    «Если изменения цели в рамках процесса ПР не предполагается, то следует выбрать группу методов со статичной целью» ( FST) ;

• 2.    «Если в текущей задаче отсутствуют неизвестные или неточные данные, то рекомендуется выбрать группу методов, способных работать только с заранее известными точными данными»;

  • 2.1.    «Если в текущей задаче важно отсутствие компенсации критериев, то следует выбрать группу методов, без компенсации критериев»;

    • 2.1.1.    «Если в текущей задаче присутствуют качественные данные, то рекомендуется выбрать группу ММПР, которые могут работать как с качественными, так и с количественными данными»;

      • 2.1.1.1.    «Если в текущей задаче присутствуют отрицательные значения, то необходимо выбрать методы, в которых отсутствуют ограничения на использование отрицательных значений» ( MAVT , TOPSIS , VIKOR);

      • 2.1.1.2.    «Если в текущей задаче только положительные значения, то следует использовать методы, в которых применяются только положительные значения» ( SAW , DEA );

    • 2.1.2.    «Если в текущей задаче есть только количественные данные, то рекомендуется использовать группу методов, которые работают только с количественными данными»;

      • 2.1.2.1.    «Если в текущей задаче существуют иерархические отношения между критериями, то необходимо выбрать методы, в которых рассматриваются иерархический вид критериев» ( AHP );

      • 2.1.2.2.    «Если в текущей задаче отсутствуют иерархические отношения между критериями, то необходимо выбрать методы, для которых не является важной иерархия критериев» ( ANP , BWM) ;

  • 2.2.    «Если в текущей задаче несущественно отсутствие компенсации критериев, то следует выбрать группу методов, с компенсацией критериев»;

    • 2.2.1.    «Если в СППР существует БД ситуаций и в ней присутствует подобная текущей, то рекомендуется выбрать ММПР, использующие БД похожих ситуаций» ( CBR );

    • 2.2.2.    «Если отсутствует БД ситуаций или в ней нет подобной текущей, то необходимо выбрать ММПР, не требующие БД похожих ситуаций» ( ELECTRE , PROMETHEE) ;

Одной из особенностей данного набора правил является отсутствие строгих ограничений на выбор определённой группы ММПР (ключевые слова - рекомендуется и следует ). Однако, использование именно указанных групп ММПР позволит ЛПР существенно сократить трудоёмкость процесса ПР и время ПР, что особенно характерно в случае с неопределёнными данными. Зачастую использование ММПР с «излишней функциональностью» может привести к существенному усложнению процесса получения и интерпретации результатов, тем самым нивелируя положительные стороны предлагаемой модели.

На основании изложенного предлагается следующая классификация ММПР по их ограничениям, представленная на рисунке 4. Среди всех 15 рассмотренных в данной статье ММПР лишь 4 позволяют учитывать неточные или неопределённые данные при работе ( GRA, MAUT , SMART , FST), также большая часть методов обладает компенсацией критериев ( SAW , DEA , MAVT , TOPSIS , VIKOR , AHP , ANP , BWM) .

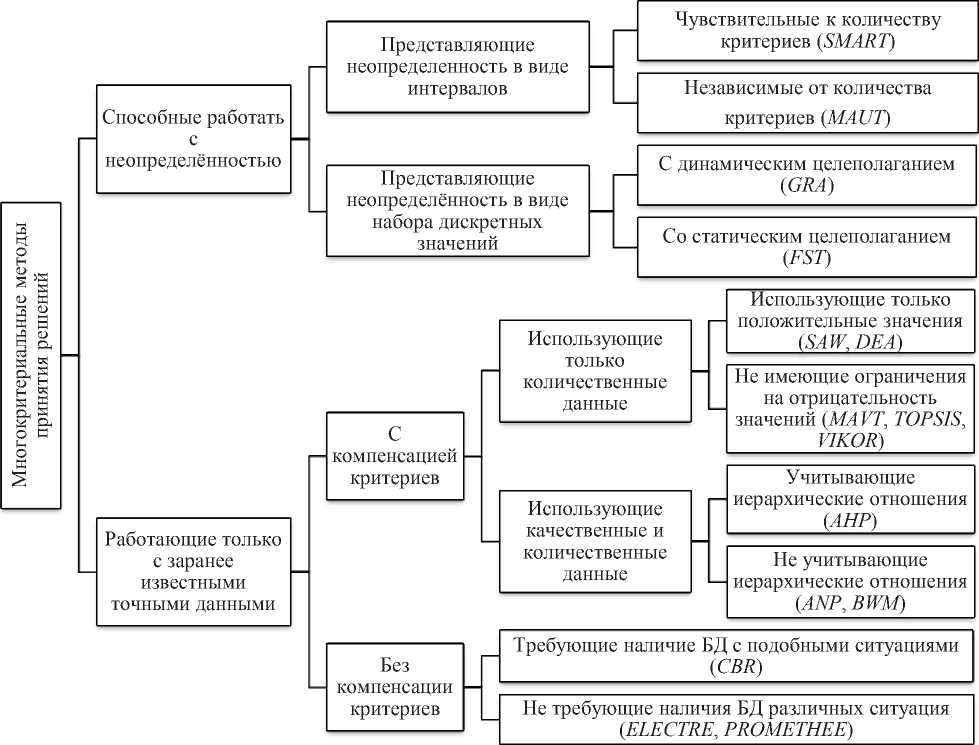
Рисунок 4 - Предлагаемая классификация ММПР по их ограничениям

Важным дополнением к разработанной классификации является классификация ММПР по основным типам решаемых ими проблем. Их комбинация обладает следующими преимуществами относительно имеющихся научных подходов:

• ■    повышение прозрачности процесса ПР, качества принятых решений, удовлетворённости ЛПР полученным решением;

• ■    сокращение времени на выбор подходящего ММПР и работу с выбранным ММПР;

Заключение

Проведённый анализ основных ММПР выявил, что многие методы, несмотря на разнообразие их методологий, обладают схожим набором ограничений и недостатков. Процесс ПР с помощью изученных ММПР связан со сложностью формализации предпочтений ЛПР. В связи с этим приведены список и классификации основных подходов к данной формализации. Ограничения ММПР послужили основой предлагаемой систематизации. Среди них можно выделить: ограничения по типам данных и их точности, а также ограничения по количеству критериев и наличию их компенсации.

Предложенная систематизация ММПР может быть полезна при разработке СППР, использующих рассмотренные в работе методы, а также ЛПР, которые для решения конкретной многокритериальной задачи стоят перед выбором ММПР. Разработанный принцип актуален в ситуациях ПР с большим количеством альтернатив и малым набором критериев. Предложенная в работе классификация позволяет с помощью системы правил отбирать наиболее подходящие методы. Это создаст для ЛПР возможность оказывать непосредственное влияние на процесс выбора ММПР, тем самым повышая его прозрачность и удовлетворённость полученным решением. Данный подход позволит сократить время на отбор ММПР и на его работу путём рекомендации наиболее эффективных ММПР при указываемых данных или ситуации.