Анализ и оптимизация многокаскадных усилительных структур

следования применительно к n последовательно соединенным каскадам усилителей.

диапазона в настоящее время предъявляются повышенные требования к линейности характеристик приемных систем. И хотя фундаментальные идеи борьбы с нелинейными искажениями (использование прямой и обратной связи, предыскажений и т. д.) известны давно, исследования в этом направлении неуклонно продолжаются, и даже наблюдается новая волна интереса к этой тематике. Какие бы высокие показатели линейности ни были достигнуты, их всегда можно улучшить. Современные приемные системы обычно включают в себя входные транзисторные многокаскадные малошумящие усилители, т. к. один каскад, как правило, не обеспечивает необходимой величины коэффициента усиления. Несмотря на то что исследованию многокаскадных усилителей посвящено много работ, в том числе фундаментальных [1; 2], в них не отражена важная роль фазовых соотношений между компонентами различного происхождения в составе комбинационных продуктов. Опыт показывает, что имеет смысл оптимизировать не только каждый каскад, но и усилитель в целом. В [3] рассмотрена возможность полной компенсации искажений 2-го или 3-го порядка в двухкаскадном усилителе с учетом фазовых соотношений продуктов нелинейности на основных частотах и высших гармонических и комбинационных составляющих каждого каскада. Настоящая работа посвящена развитию предложенных методов ис-

1.    Нелинейные искажения 2-го и 3-го порядков

При оптимизации усилительных структур с компенсацией нежелательных спектральных составляющих целесообразно представить нелинейные характеристики каждого из каскадов усилителя в виде степенного ряда

U BblX = f ( U BX ) =

= K (U + — S' U 2T + — S " U 3T), вх          вх          вх что позволит наглядно и достаточно полно рассмотреть основные закономерности нелинейного взаимодействия. При этом сущность выявленных процессов сохраняется также при использовании и более сложных математических моделей.

Возможность компенсации на выходе тех или иных продуктов нелинейности определяется соотношением знаков и величин коэффициентов K , S ', S ''. Для обычных режимов работы входных усилителей характерно знакочередование коэффициентов, причем S " <  0  ( S "  = - S "|).

Различным схемам включения усилителей на полевых транзисторах соответствуют следующие сочетания знаков коэффициентов:

схема с общим истоком (ОИ) –

U„b,x = K(U6x + 1S'IU2x -1S"Iu3x); вых        вх         вх          вх схема с общим затвором (ОЗ) – ивыx = K(u8x -1S'Iu2x -1S"Iu3x);

вых        вх         вх          вх

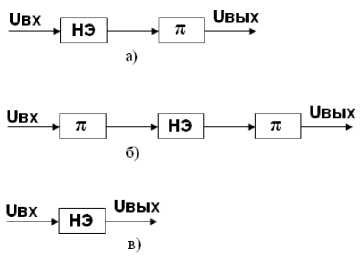
Рис. 1. Макромодели усилителей: a) усилитель с общим истоком или общим эмиттером; б) усилитель с общим затвором или общей базой; в) усилитель с общим стоком или общим коллектором схема с общим стоком (ОС) –

U = K ( U + ¹ S ' U ² - ¹ S '' U ³ ). вых вх вх вх

Для биполярных транзисторов это соответствует включению по схеме с общим эмиттером (ОЭ), общей базой (ОБ) или общим коллектором (ОК).

Для упрощения математических выкладок будем использовать макромодели, представленные на рис. 1. Нелинейный элемент (НЭ) в этих макромоделях имеет характеристику

K ( U + ¹ ₂ S ' U ² - ¹ ₆ S '' U ³), U =± U вх .

В работах [3–5] показано, что в двухкаскадном усилителе для компенсации продуктов нелинейности на основных частотах, интермодуляционных составляющих 2 ω ₁ – ω ₂, 2 ω ₂ – ω ₁ и третьих гармоник 3 ω ₁, 3 ω ₂ инвертирование фазы между НЭ каскадов не должно происходить. И наоборот, для компенсации на выходе усилителя продуктов интермодуляции ω ₁ ± ω ₂ и вторых гармоник 2 ω ₁, 2 ω ₂ между НЭ первого и второго каскадов фаза напряжения должна измениться на π .

Нелинейные свойства усилителей на полевых транзисторах, заданных эквивалентными схемами, в первую очередь определяются нелинейным характером источников тока, управляемых напряжением [1]. Именно эти элементы являются доминирующими источниками нелинейности. Используемая в работе эквивалентная схема полевого транзистора приведена на рис. 2. Моделирование многокаскадных усилителей на полевых транзисторах проводилось в программе AWR Microwave Office. Посколь к у управляемый источник тока в схеме с ОИ уже обладает инвертирующими свойствами, то для компенсации в последующем каскаде нелинейных искажений 3-го порядка необходимо дополнительно

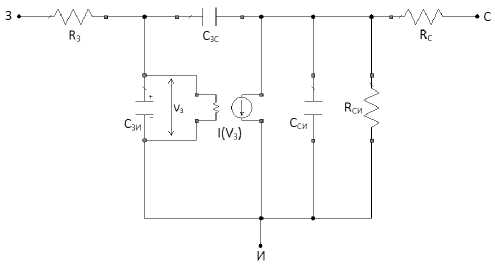
Рис. 2. Эквивалентная схема полевого транзистора

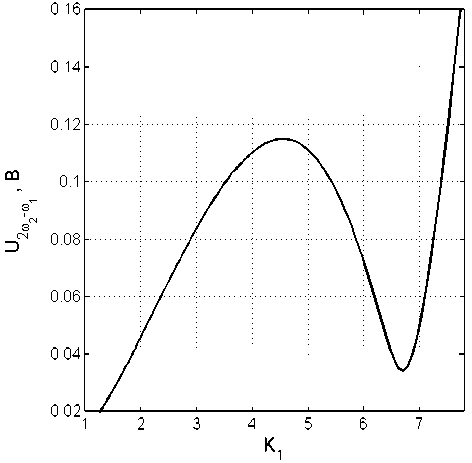
Рис. 3. Зависимость уровня продукта интермодуляции 2 ® 2 - ® ! на выходе 2-го каскада от коэффициента усиления 1-го каскада в структуре ОИ — п — ОИ

1 ''           2

— Sn K n K n - 8

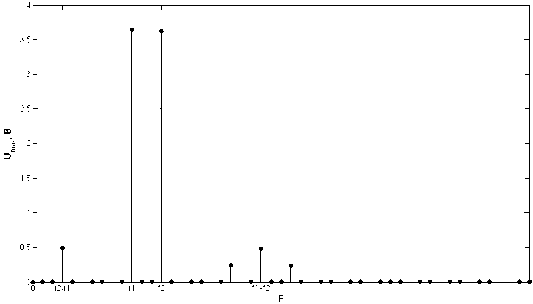
Рис. 4. Спектр сигнала на выходе трехкаскадного усилителя ОИ — ОИ — п — ОИ при компенсации нелинейных искажений 3-го порядка

фициенты Sn , Sn рассчитываются по рекуррентным формулам: '                                                                                                        '             '''

QQ' ■ ^Sn ^-1              4- d S n S n Z- , ^Sn ^-1

Sn Sn +       , Sn Sn + 3         +

KK2

n -1                        n -1

Условия отсутствия на выходе n -го к а скада составляющих 2-го или 3-го порядка S n - 0, S n - 0 соответственно.

Запишем эти условия через коэффициенты разложения нелинейных характеристик каскадов. Для компенсации нелинейных искажений 2-го порядка должно выполняться условие ''    '

S n + S n ^¹ + S n ^- 2   + ... +--- S ----0.    (2)

n K n - 1 K n - 1 K n - 2        K n - 1 ... K 1

Если заданы коэффициенты квадратичной не '

линейности Si для всех каскадов, то (2) показы- вает, в каком соотношении должны находиться коэффициенты усиления отдельных каскадов Ki . В принципе задача имеет множество решений, но условие (2) лучше рассматривать как ограни- чение на коэффициент усиления предпоследнего каскада Kn-1:

''

_ Sn ^-1 _ S n - 1 + S n ^-2 / K n - 2 _

Kn -1 -        -                      - n1 SS n                 n(3)

_ Sn-1     1 Sn-2           1

-----:----:--....

' K ' K    ...K n n — 2 n          n — 2 1 n

Чем больше значения коэффициентов усиле- ния предшествующих каскадов, тем меньше их вклад в (3). Поэтому естественно предполагать, что первый член в (3) является преобладающим. Детальный анализ возможных знаков Kn-1, Sn' -1, Sn' показывает, что для компенсации нелинейных искажений 2-го порядка между НЭ предпоследнего и последнего каскадов должно произойти инвертирование фазы сигнала. Предшествующие им n - 2 каскада могут иметь произвольные схемы включения.

В соответствии с вышесказанным при выполнении условия (3) в структуре типа ОИ – … – ОИ – ОИ будет наблюдаться компенсация продуктов нелинейности 2-го порядка ® i ±® 2 , 2 ® i , 2 ® 2 . Другие варианты включения двух последних каскадов: ОЗ – ОИ, ОС – ОЗ, ОЗ – ОС, ОИ – ОС с практической точки зрения менее интересны.

Для компенсации нелинейных искажений 3-го порядка коэффициент усиления предпоследнего каскада K n - 1 должен удовлетворять уравнению

S22 K 2_! + 3S„( Sn_! + Sn-2-) Kn_! + n n        n n               I

K n - 2

''

+ 5 I  1

'

+ 3 S n - 1 S n ^{- 2}

K n- 2

5 n - 2

⁺ 1^

K n - 2

= 0.

В уравнении (4), так же как и в (3), предшествующие каскады вносят тем менее существенный вклад, чем ниже их номер и больше коэффициент усиления. Преобладающим является член уравнения, у которого отсутствует знаменатель. Кроме значения K_{n -} 1 , уравнение (4) определяет еще схему включения предпоследнего и последнего каскадов. Анализ возможных знаков K_n , K_{n - 1}, S_{n - 1}, S_{n - 2} свидетельствует, что между НЭ двух последних каскадов не должно быть инвертирования фазы. В противном случае все компоненты уравнения (4) оказываются синфазными, и компенсация невозможна. Из двух возможных решений уравнения (4) следует выбрать то, которое имеет большее значение.

Неинвертирующими свойствами обладают, в частности, структуры ОИ – ОЗ и ОЗ – ОЗ. Однако в этом случае необходимо согласование выходного сопротивления ( n - 1)- го каскада и низкого входного сопротивления n -го каскада. Причем согласующее устройство не должно вносить существенных искажений в характер протекающих нелинейных процессов. Могут быть использованы каскады с ОИ и дополнительным инвертированием фазы между двумя последними каскадами, т. е. структур типа ОИ– … – ОИ — п — ОИ.

Рассмотрим результаты моделирования трехкаскадного усилителя с каскадами ОИ – ОИ – п — ОИ. В такой структуре при значении коэффициента усиления 2-го каскада K2 = 5.7 (при этом Ki = Kз = 12) будет наблюдаться компенсация нелинейных искажений 3-го порядка. На рис. 4 показан спектр сигнала на выходе 3-го каскада при двухчастотном воздействии. Видно, что в спектре сигнала присутствуют в основном составляющие 2-го порядка ®i + ®2, Ю1 - ю2, 2®1, 2^2. Нелинейные составляющие 3-го порядка 2®2 -®1, 2®1 - ®2 имеют существенно меньшие значения по сравнению с обычным включением ОИ – ОИ – ОИ для того же самого набора схемных параметров. В частности, уровень интермодуляционных продуктов 2®2 - ®1 снижается на 28 дБ.

Перейдем к более детальному анализу условия компенсации составляющих 3-го порядка (4) при n = 3:

S₃ K 2 ² + 3 S ₃( S 2 + 5 1 / K 1 ) K 2 +

' '                       ''

+ s ₂"₊ 3 SS + S L = o.

2 K ₁     K ₁ 2

Соотношение (5) можно интерпретировать как уравнение второго порядка для нахождения значения коэффициента усиления 2-го каскада K ₂, при котором имеют минимум нелинейные искажения 3-го порядка. При этом K ₁ считается варьируемым параметром. Отсюда следует, что чем больше квадратичные члены S ₁^' , S ₂^' , S ₃^' , тем большие значения K ₂ можно устанавливать, а следовательно, тем проще достигаются условия компенсации нелинейных искажений 3-го порядка. При снижении K ₁ условия компенсации также улучшаются. Желательно, хотя и не обязательно иметь в первом каскаде K >  0. Как видно, структура НЭ₁ – НЭ₂ – НЭ₃ без межкаскадного инвертирования оказывается более предпочтительной для компенсации составляющих вида 2 ® 2 - ® 1 , 2 ® 1 - ® 2 , чем структура НЭ 1 — п — НЭ 2 — НЭ 3 . Поэтому с целью создания благоприятных условий компенсации в структуре ОИ – ОИ – ОИ для нейтрализации инвертирования в самих каскадах необходимо ввести дополнительное межкаскадное инвертирование фазы ОИ — п — ОИ — п — ОИ. Сказанное иллюстрирует рис. 5, на котором показана интермодуляционная составляющая 2 ® 2 - ^Ю 1 на выходе 3-го каскада в зависимости от уровня входного воздействия. Здесь сплошная линия соответствует дополнительному инвертированию фазы между первым и вторым каскадом (т. е. вариант ОИ — п — ОИ — п — ОИ); пунктирная линия рассчитана без этого инвертирования (ОИ — ОИ — п — ОИ).

Отметим еще следующее. Для двухкаскадного усилителя невозможно одновременное подавление нелинейных искажений 2-го и 3-го поряд-

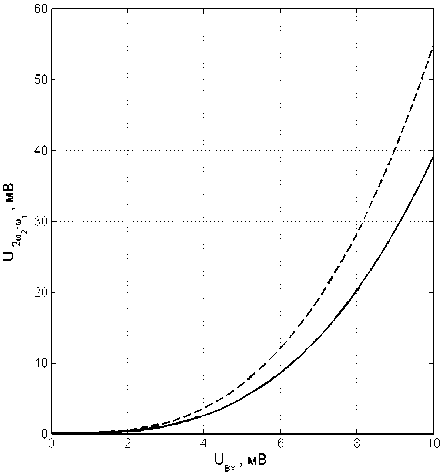
Рис. 5. Зависимость продукта интермодуляции 2 ^ - № от уровня входного воздействия ОИ — п — ОИ — п — ОИ (сплошная линия) и ОИ — ОИ — п — ОИ (пунктирная линия)

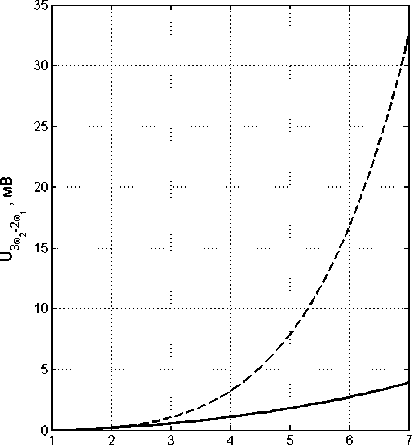
К1

Рис. 6. Зависимость продукта интермодуляции 3 ф 2 - 2 ф 1 от коэффициента усиления 1-го каскада в структуре ОИ – п — ОИ (сплошная линия) и ОИ — ОИ (пунктирная линия)

ков при условии одинаковых знаков S ₁ и S ₂. Это связано с тем, что в предлагаемом подходе компенсация продуктов нелинейности 3-го порядка происходит за счет взаимодействия основных частот с продуктами нелинейности 2-го порядка. Это предполагает достаточно высокий уровень последних. Для трехкаскадного усилителя это утверждение уже не столь категорично. Если в первом и втором каскадах достаточно большие квадратичные члены S i , S₂, и K i >  0, а между вторым и третьим каскадами осуществить узкополосную связь, то условие компенсации

( S 3 K 2 + S 2 ) K 2 + 3 S i S 2 K 1 + S 1 = 0             (6)

хотя и трудно достижимо, но в принципе реализуемо подбором значений K ₁ и K ₂. При этом для появления в (6) противофазного члена обязательно должно быть K i >  0. Хотя знак K 2 в (6) не играет роли, на его значение налагается более серьезное ограничение, чем в (5).

2.    Нелинейные искажения высших порядков

Представляет интерес поведение продуктов интермодуляции порядков выше третьего при выполнении условия компенсации (2) или (4). Для этого в характеристиках НЭ необходимо рассматривать большее число членов (m) 1'2     S m вых ( вх + вх + ... +         вх) .

2              m !

Как уже отмечалось, обычно для входных усилителей наблюдается знакочередование ко- эффициентов ряда: а именно S(m) и S(m+2) имеют противоположные знаки. Например, S(2) > 0, S(3) < 0, S(4) < 0, S(5) > 0 и т. д. Такое знакочере- дование вполне согласуется с тем, что для ти- пичной зависимости уровня m-й гармоники от входного напряжения начальный участок представляет собой параболу m-го порядка, а затем наступает насыщение. Такой переход имеет мес- то только в случае, если первый член в выра- жении для m-й гармоники

S ( m )

m - 1

2 m !

^m U ₀

и следующий член

S ( m + 2) m 2 ^{m + i}( m + 2)!

U

m + 2

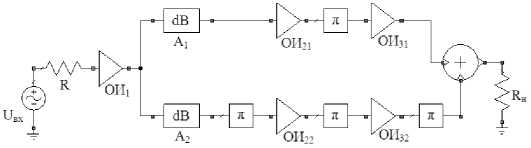
Рис. 7. Структура для одновременной компенсации нелинейных искажений 2-го и 3-го порядка растают нелинейные искажения всех четных порядков. В последовательных структурах это неизбежно, т. к. компенсация нелинейных искажений 3-го порядка достигается за счет повышения уровня составляющих 2-го порядка. Несмотря на последнее обстоятельство, в целом имеющие место закономерности при компенсации (4) можно оценивать как положительные. Такой вывод следует из того, что составляющие нечетных порядков вида p®i - (p - 1)^2 более опасны для входных устройств по сравнению с составляющими четных порядков, т. к. последние легче отфильтровать.

В работе [3] предложен способ устранения нелинейных искажений четных порядков путем балансного включения двух последовательных структур, в каждой из которых скомпенсированы нелинейные искажения 3-го порядка. В n -каскадной структуре данный подход не приведет к полной компенсации нелинейных искажений 2-го и 3-го порядка, если включить балансным способом только два последних усилителя. Однако если обеспечить поступление сигнала в каждое из плеч в определенных, неравных пропорциях (рис. 7), то удается полностью подавить нелинейные искажения 2-го и 3-го порядка. Структура похожа на балансное включение, но плечи не идентичны. Неравномерное деление сигнала после 1-го каскада достигается при помощи аттенюаторов A ₁ и A ₂. При поиске оптимального решения можно выбрать более простой путь, когда каждое из плеч настраивается на минимум нелинейных искажений 3-го порядка в данном плече с последующим балансированием составляющих 2-го порядка из верхнего и нижнего плеч. Однако лучшие результаты достигаются при решении оптимизационной задачи в целом. Надлежащим подбором параметров аттенюаторов и коэффициентов усиления каскадов ОИ₂₁ и ОИ₂₂ можно получить чистый спектр на выходе предлагаемой структуры, который показан на рис. 8. Практически полное подавление интермодуляционных составляющих 2-го и 3-го порядка наблюдалось при K 21 = 5.4, K 22 = 6.8. С помощью аттенюаторов соотношение мощности сигнала

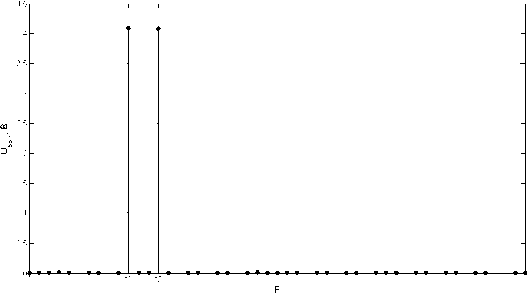
Рис. 8. Спектр сигнала на выходе многокаскадного усилителя при компенсации нелинейных искажений 2-го и 3-го порядка между 1-м и 2-м плечом настраивалось в соотношении 0.55: 0.45.

Заключение

Проведенные в данной работе теоретические и экспериментальные исследования убедительно свидетельствуют о том, что учет фазовых соотношений компонент в спектре сигнала на выходе каждого усилительного каскада, а также упорядочение фаз этих компонент позволяют эффективно устранять нелинейные искажения тех или иных порядков. При этом особое внимание следует обращать на фазовые соотношения компонент на выходе предпоследнего каскада.

Работа выполнена в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы по договору № 14. В37.21.0620.