Анализ и расчет параметров движения лесовозных автопоездов

До настоящего времени тяговые расчеты для определения допустимой нагрузки, скорости движения, производительности автопоездов выполнялись традиционными способами, основанными на методе равновесных скоростей. Эти способы уточнялись и применялись к проектированию лесовозных дорог и организаций лесотранспортных работ М. И. Кишин-ским, М. М. Коруновым, Р. П. Лахно, В. А. Горбачевским, Б. А. Ильиным, А. П. Ливановым, В. А. Носи-ковым, Э. О. Салминеным и другими исследователями. Однако на современном этапе традиционные методы расчетов не удовлетворяют возросшим требованиям ввиду того, что не учитывают многие факторы, влияющие на показатели движения. Проведенные исследования показали, что графики движения, рассчитанные по методу равновесных скоростей, не адекватны фактическим. Результаты расчетов не обеспечивают достаточной точности, в частности: расхождение по времени движения по всему маршруту составляет 40–45 % в сравнении с фактическим, а на отдельных участках отличается вдвое.

На кафедре технологии и оборудования лесного комплекса Петрозаводского государственного универси- тета (ТОЛК ПетрГУ) и в Карельском НИИ лесного комплекса (ПетрГУ) на протяжении значительного времени проводилась работа по совершенствованию методов тяговых расчетов и разработке алгоритмов и программ для моделирования движения лесовозных автопоездов и определению показателей движения в конкретных условиях эксплуатаций. Результаты исследований изложены в работах [1–4].

В работе [1] на основе решения дифференциального уравнения движения автопоезда:

a - bv2 = ^^v— + ^G + iG + kMAv2 + G —— + G — (1) g ds                     RгR получена расчетная зависимость:

D 2 _ A — Bv0,

Bv = -cs— + p + A ,(2)

где A = a - Gro ± Gi + GC^ B = b + kMAv 2; G - вес ав-Rг топоезда, кгс; Rг – радиус горизонтальной кривой; Сг – коэффициент, учитывающий увеличение сопротивления движению на горизонтальных кривых; Rв – радиус вертикальной кривой; а и b – коэффициенты зависимости, аппроксимирующей тяговую или тормозную характеристику автопоезда в виде F = a–bυ2; k, Δ, Ω – соответственно коэффициент сопротивления воздушной среды автомобиля, коэффициент, учитывающий дополнительное сопротивление от прицепов, лобовая площадь автомобиля, кв. м.

p = G [ C 1^{( e} CS - 1)+ s ]^; C = 2 Bg ; ^e CS = * ,           ⁽³⁾

где R – радиус вертикальной кривой, м.

Эта зависимость дает возможность определения скорости движения в зависимости от начальной скорости пройденного автопоездом расстояния на вертикальных выпуклых и вогнутых кривых, прямолинейных в профиле участках с учетом изменений тягового усилия и сопротивления воздушной среды с изменением скорости движения, непрерывного изменения сопротивления движения от уклона на вертикальных кривых, дополнительного сопротивления на горизонтальных кривых при движении автопоездов с неповоротными тележками на горизонтальных кривых.

Для облегчения и ускорения расчетов разработаны таблицы для определения x = b(S) , ρ = f(S) , A , B , приведенные в работах [1–4]. С использованием таблиц достаточно быстро и эффективно решаются задачи по определению скорости движения в зависимости от υ₀ и расстояния, пройденного автопоездом с учетом всех перечисленных выше факторов, во всех режимах движения (движение накатом, торможение двигателем и моторным тормозом).

Для решения этой и обратной задачи (определения расстояния, пройденного автопоездом при изменении скорости от υ0 до υ) без применения таблиц диффе- ренциальное уравнение движения автопоезда можно представить в следующем виде:

С ■ v ■ dv - T ± к ■ G ,

1 ds где T - А -Bv2; С. = —; к - —.

¹ g R

Из начальных условий при — = S 0 , и₀ = и

( T ■ S + k- S -) ■ 2 v ² =----------- ²------ + v ₀2 .

С i            ⁰

Пример. Дано: автопоезд МАЗ+МАЗ-63781 с полной нагрузкой ( G = 48000 кг) начал движение на вертикальной выпуклой кривой радиусом 1500 м со скоростью 12 м/с на восьмой передаче КПП. Продольный уклон в начале кривой i = -0,015; to = 0,02. Определить скорость движения на расстоянии 60 м от начала кривой. Из соответствующих таблиц [3, 4] находим a = 1460; B = 1,41.

T - 1460 - 48000 ■ (0,02 - 0,015) - 1,41 ■ 12² = 1036,9;

к - 48000 - 32; С - 1,073.55000 =

1500                  9,81

(1036,9 ■ 60 + ³² ■ ⁶⁰ ) ■ 2

v ²  ---------------²------+ 12² -189,64, v - 13,77 м/с.

При решении этой задачи с использованием зависимости (2-3) и =13,76 м/c, то есть для решения практических задач точность достаточна. Для решения обратной задачи определения расстояния, которое проедет автопоезд при изменении скорости от и₀ до u k , уравнение (5) преобразуется к виду:

к ■ S ² + 2 ■ T ■ S + ( v ₀ ² - v_k ²) ■ С 1 - 0 . (6)

Таким образом, по точности расчета показателей движения разработанный метод расчетов не уступает известному табличному методу, обеспечивающему в отличие от традиционных методов достаточно точные и достоверные результаты, ввиду учета большего числа факторов, влияющих на показатели движения. Кроме того, новый метод дает возможность успешно решать и обратную задачу - определение расстояния при изменении скорости движения от u₀ до u .

На участках вертикальных кривых в связи с непрерывным изменением уклона изменяется суммарное сопротивление движению, при этом на выпуклых вертикальных кривых сопротивление непрерывно уменьшается, а на вогнутых - возрастает.

При этом на вертикальной выпуклой кривой непрерывное увеличение скорости движения обеспечено, если A - Bu₀² > 0; на вогнутой вертикальной кривой снижение скорости имеет место, если A - Bu₀² < 0.

При невыполнении этих условий, при прохождении точки, где А и = 0, вектор изменения скорости меняется на противоположный.

Как известно, экстремальные значения непрерывных функций определяются в точках, где первая производная равна 0. Для определения S возьмем первую производную от зависимости (6).

Следовательно, v2/ - 0 - 2 ■ T / С + 2 ■ S ■ к / С; — --T.          (9)

k

В точке экстремума Т = 0, следовательно:

Так как в диапазоне 12-13,76 м/с величина T изменяется, с целью уточнения решения, величину T можно принять равной среднеинтегральному значению в указанном диапазоне:

() 2

v ² ----²--------

С 1

2 + v 0.

T -

A^v 0

Av 0³

л Av ³

- Av +---

______________ 3 .

^{v - v} 0

Среднеинтегральное значение T = 985,73.

S -

- 2 ■ T ± V (2 ■ T ) ² - 4 ■ к ² ■ ( v ₀ ² - v / ) ■ С 1 ■ 5 .

2У

Пример. Автопоезд МАЗ-6303-26+МАЗ-63781 ( G = 48000 кг) начал движение на вертикальной кривой радиусом 10000 м, i = 0,0136, to = 0,03. Движение осуществляется на восьмой передаче 5 = 1,048; a = 1047; B = 0,972. Определить расстояние до точки экстремума и экстремальное значение скорости. Остальные условия те же.

T - 1047 - 48000(0,030 + 0,0136) - 0,972 ■ 17² - - 1327,9;

Пример. Определить расстояние, которое пройдет автопоезд МАЗ-6303-26 на вертикальной кривой радиусом 1500 м при изменении скорости движения от и₀ = 12 м/с до и_к = 13,75 м/с, G = 48000 кг; начальный уклон i = -0,015; to = 0,02.

1327,9 ■ 10000

- 276,5 м;

v² - ^{2( - 1327},9 ■ ^{2765 +} 4,8 ■ ²⁷⁶,5²/²) + 289 - 217 26; 5128                              ’ ’

- 985,73 ■ 2 ± 4 ■ 985,73 ²

- 4 ■

S -

2 ■ 48000/1500

■ ( - 13,75² + 12²) ■ 4893 ■ 1,073

- 60,03 м.

v - 14,74 м/с (рис. 1).

В таблице 1 представлены значения скорости в диапазоне от 50-300 м от точки экстремума при иэ=14,74 м/с.

Таблица 1

Скорость в диапазоне от 50–300 м от точки экстремума при υэ=14,74 м/c

S, м	υ, м/с	υ, км/ч
50	14,82	53,52
100	15,05	54,18
150	15,43	55,55
200	15,95	57,42
250	16,61	59,8
300	17,36	62,5

Пример. Автопоезд МАЗ-6303-26+МАЗ-63781 входит на вертикальную выпуклую кривую радиусом 1500 м. Определить ограничение скорости на кривой. φ = 0,15; i = 0,02; ω = 0,03; A = -9600.

S_B = V2 - 1500 • 2,2 = 81,2 м.

Так как по условиям безопасности движения автопоезд должен остановиться минимум за 10 м до препятствия, следовательно, S_вр (расчетное расстояние видимости) равно 71,2 м.

v огр

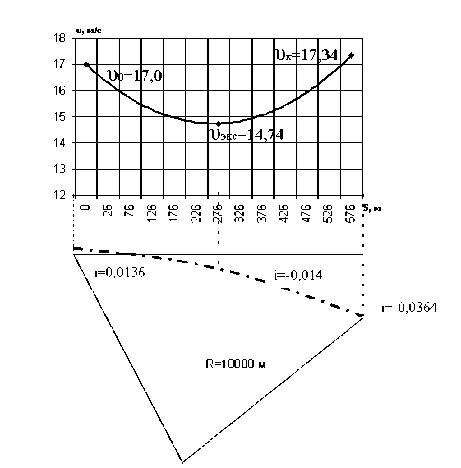
Рис. 1. Расстояние до точки экстремума и экстремальное значение скорости

' 9600 • 71,2 — 32 • 71,22/2 .... .

2-------------------— = 15,55 м/с.

1,037 • 48000/9,81

При том же расстоянии видимости в закрытой местности на вогнутой вертикальной кривой υ _огр = 17,53 м/c (63,11 км/ч), на прямолинейном в профиле участке 16,57 м/c (59,66 км/ч).

Выведенные на основе дифференциального уравнения движения в виде (4) расчетные формулы позволяют определять скорость движения υ в зависимости от пройденного автопоездом расстояния и начальной скорости υ₀ , а также пройденное расстояние при изменении скорости от υ₀ до υ_k .

Для определения времени движения на участке S0–S1 при изменении скорости от υ0–υ1 решается уравнение T = C d 2S + kG где Т — среднеинтегральное тяговое dt2        , усилие на рассматриваемом участке.

При k > 0

arcsin

ТАЛ + U А² А^{2     2} + А²¥ А² -    ^

² A 3 A 2 ⁺ V ⁴ A 3 A 2   ⁴⁽ A 1 ⁺ A 3 ⁾⁽ A 2    A 1 )

Расчетная скорость движения на участках ограничения не должна превышать такую величину, при которой будет обеспечена остановка автопоезда перед препятствием в пределах расстояния видимости.

t 1,2 =

При k < 0

2( A 2 + A 3² )

kC

У

. (11)

Расстояние видимости на вертикальных выпуклых кривых, в закрытой местности (косогор, наличие в полосе отвода кустарников, деревьев) определяется по известным зависимостям (3, 4).

t 1,2 =

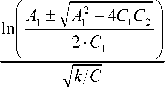
Исходя из формулы (5) и преобразуя ее с учетом того, что на участке ограничения на расстоянии видимости необходимо остановить автопоезд (т. е. конечная скорость равна 0), а начальная скорость движения на участке не превысит υ _огр.

Здесь A 1 = — —; k

A ² k S ; A ³ = ^{V 0} Is ^;

V огр

- A T S -

kS ²

C 1

На пря молин ейном в профиле участке

L — At vогр = 2 -—, где Aт = G^+Gi+G® C1

^c 1 = ⁽ TH + v ^{o )/2} П ; C 2 = ⁽ TH — v 0 ^)/2 н . kC C kC C

Пример. Автопоезд ТМ-45 (автомобиль КаМАЗ53228 с прицепом ТМЗ-8966-10) весом 41000 кг начал движение на вертикальной выпуклой кривой радиусом 5000 м; продольный уклон в начале участка i = 0,001, ω = 0,018; υ = 8,56 м/с. Длина участка 150 м. Определить время движения на участке. Из таблицы,

приведенной в работе [4], определяем a = 1101, B = 1,2.

A = 1101 - 41000(0,001 + 0,018) = 332, k = 4¹⁰⁰⁰ = 8,2.

Для рассматриваемого случая по формуле (5) определим скорость в конце участка υ = 11,42 м/с.

T = - 332 - 8,56 + 1,2 - 8,56- + 332 - 11,42 - 1,2 -       = 211,42;

,,      ,,     ,

C =

9,81

■ 1,04 = 4430,17;

C 1 =

211,42     8,2

8,2    4430,17

+ 8,56

2 8,2 4430,17

= 112,37;

211,42

8,2

C 2

8,2

4430,17

8,56

2 8,2 4430,17

- 86,59;

211,42

A = 150 +---— = 175,78;

1 ,

t 1,2 =

, f 175,78 ± J 175,78 2 - 4 - 112,37 - ( - 86,59) ln

I                    2 - 112,37

8,2 4430,17

= 15,62 с.

Пример. Автопоезд ТМ-45 с грузом ( G = 41000 кг) начал движение на вертикальной вогнутой кривой радиусом 6000 м на восьмой передаче КПП; продольный уклон в начале участка i = 0,005, ω = 0,018, υ ₀ = 8,56 м/с. Определить скорость движения на расстоянии 100 м от начала кривой и время движения. a = 1101, B = 1,2.

= 6,83;

2 - 1,2 ■ 9.81 c =----------- 41000 - 1.04

= 0,000552;

e c = 1,05675; _L = _{0 946} - e^cs

P =

41000     1

6000 [ 0,000552

(0,946 - 1) + 100

= 18,5;

Bv² = 158 —58—,----,5—18,5 = 202,74; v = 13,8 м/с.

1,05675

- 158 - 14,5 + 1,2 ■ — ⁵ + 158 - 13,8 - 1,2 ■     8

T =---------------- ³------------------ 3— = 82,24;

- 14,5 + 13,8

A 1 =

82,24

6,83

- 12,04; A ₂ =

82,24 6,83

- 100 = - 87,96;

A 3 =

-

8,56

6,83

- 369,20;

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

И ОСНОВНЫЕ ВЫВОДЫ

Выведенные зависимости позволяют определить показатели неустановившегося движения лесовозных автопоездов во всех возможных режимах и в отличие от традиционных методов расчетов, применяемых на лесовозном автотранспорте, обеспечивают достаточную точность и адекватность расчетов. По точности расчета показателей движения предложенный метод расчетов не уступает разработанному ранее табличному методу, обеспечивающему в отличие от традиционных методов достаточно точные и достоверные результаты, ввиду учета большего числа факторов, влияющих на показатели движения. Максимальное расхождение на контрольных участках между фактическим и расчетным временем движения не превышает 6 %, графики расчетных и фактических показателей движения имеют хорошую сходимость по характеру изменения скорости, режимов движения и используемых передач.

Проведенные исследования позволили вывести расчетные зависимости для определения основных показателей движения (скорости, времени движения, пройденного автопоездом расстояния) во всех режимах движения с учетом всех основных факторов, влияющих на показатели движения. Полученные зависимости могут использоваться для получения исходных данных при решении различных техникоэкономических задач при планировании работы автотранспорта в лесозаготовительных предприятиях; расчета обоснованных норм выработки автопоездов, с учетом особенностей плана и профиля конкретной автодороги, в учебном процессе при проведении тяговых расчетов в рамках курсов тяговых машин и сухопутного транспорта леса. Для проведения массовых и многовариантных расчетов с использованием выведенных зависимостей разработаны модели, алгоритмы и программы, которые использовались в учебном процессе и при решении различных техникоэкономических задач в конкретных лесозаготовительных предприятиях.