Анализ и решение задач выбора с параметрической нечеткостью

Важными направлениями развития приложений теории нечетких множеств в управлении является нечеткая логика и нечеткая арифметика. Модели нечеткой логики можно рассматривать как альтернативу классическим аналитическим моделям теории управления, в частности теории принятия решений. При этом основные компоненты нечеткой логики: системы нечетких продукционных правил, нечеткие реляционные уравнения обладают рядом важных достоинств - относительной простотой синтеза системы управления в условиях нечеткой неопределенности, естественной робастностью, возможностью учета, человеческого опыта и интуиции. С другой стороны, модели и методы классической теории управления обладают несоизмеримо большими возможностями отображения разнообразных свойств систем управления (управляемость, устойчивость, оптимальность и т.п.) и обеспечивают направленность синтеза управления на их достижение. Нечеткая неопределенность может быть, при необходимости, включена в классические модели управления или принятия решений в виде параметров и переменных, оценки которых представляют собой приблизительные значения, получаемые обычно экспертным путем. Наиболее адекватным представлением таких оценок являются нечеткие числа, т.е. нечеткие подмножества, числовой оси R с функцией принадлежности ц : R ^ [0, 1]. Известны несколько разновидностей нечетких чисел, а. также соответствующие алгебры и алгоритмы, составляющие основу нечеткой арифметики и позволяющие производить необходимые вычисления в условиях нечеткости параметров и получать решение задач в нечетком виде, например, [1-4]. Сочетание классических моделей и методов учета нечеткой неопределенности в данных представляется перспективным направлением развития теории управления. Разнообразные модели принятия решений часто используют представление неопределенности параметров в форме нечетких чисел, о чем свидетельствует большое количество публикаций по этой тематике, например, [4-8]. Широкое применение классических моделей управления и принятия решений с нечеткими параметрами сдерживается рядом существенных особенностей известных методов обработки нечетких чисел:

• -    операции над нечеткими числами могут повлечь неоправданное расширение неопределенности результата, делая его зачастую практически неприемлемым;

• -    нечеткие результаты решения задач не всегда могут быть адекватно интерпретируемы из-за искажения формы нечеткого числового результата или (и) искажения естественных свойств и отношений классических моделей (например, нечеткие параметры не сохраняют тождественность уравнения при подстановке решения), что влечет снижение, а иногда и потерю адекватности моделей;

• -    существующее многообразие инструментальных программных средств решения различных математических задач принятия решений и управления, ориентированное на работу с действительными числами, не может быть использовано при обработке нечетких данных вследствие особенностей реализации арифметических операций над нечеткими числами и операций сравнения нечетких чисел.

В работах [9, 10] были предложены модифицированные треугольные нечеткие числа ЕЯ-типа и основные операции над ними, позволяющие преодолеть некоторые недостатки. Но правила выполнения операций над нечеткими числами в предложенной алгебре не совпадают с правилами выполнения аналогичных операций над действительными числами, что делает невозможным применение стандартных инструментальных программных средств решения задач управления, которые оперируют действительными числами. Для решения задач управления с нечеткими параметрами требуется либо разработка специального программного обеспечения, либо формирование такой алгебраической системы нечетких чисел, которая допускает использование стандартных пакетов (Maple, Matlab, Excel и т.п.). Очевидно, что второй путь менее затратный.

Кроме того, использование в работах [9, 10] Q -уровневого подхода к решению широкого круга задач не гарантирует сохранение исходной формы представления нечетких чисел в полученном решении, что затрудняет его интерпретацию, а иногда делает ее невозможной. Это связано с проблемой устойчивости решений на различных « -уровнях, что обуславливает необходимость анализа устойчивости решения.

Цель настоящего исследования - подобрать алгебру изоморфную алгебре, предложенной в [9, 10], обеспечивающую возможность применения стандартных программных средств решения задач, а также разработать практические критерии для анализа устойчивости решения для некоторых типов задач.

1.    Основные определения

Нечеткое треугольное число A ЕЯ-типа задается в виде тройки действительных чисел (xL,m, xR, где m - мода, a xL, xR - соответственно левая и правая границы носителя X. Функция принадлежности числа А определяется следующим образом

<

Да ⁽ x ) = <

Да = x - xL m - xL R Да = x - xR m - xR x Е [xL; т], x Е [m; xR],

0 в остальных случаях.

Нечеткие числа можно представлять в виде объединения четких подмножеств А_а множества X, каждое из которых называется « -интервалом - А_а = {х Е X 1ц д(x ) >  «}: « Е [0; 1]:

A= U «Аа.                            (2)

ае [0;1]

Правая часть равенства (2) представляет собой объединение « -интервалов, функции принадлежности которых принимают значения, равные « . Если задать конечное число n значений «, то равенство (2) позволяет свести решение исходной нечеткой задачи к совокупности n задач на соответствующих « -уровнях с параметрами, представленными четкими интервалами. Получение четкого решения на каждом « -уровне определяется выбором подходящей точки внутри « -интервала. Часто, при решении практических задач, в качестве такой точки принимается середина интервала [7].

Границы « -интервалов являются функциями обратными (1):

xL ( « ) = «т + (1 — « ) xL, xR ( « ) = «т + (1 — « ) xR.

В работе [9] была предложена алгебра P = (K ; S ₁ ) на миожестве K = {x ( « ) } ; « Е [0; 1] нечетких LL RR-чжел. Элементами множества K

x(« ) = a + b«

являются модифицированные нечеткие числа с треугольной функцией принадлежности, представленной только одной стороной треугольника, отображающей степень оптимизма или пессимизма в приблизительной оценке числа; b - коэффициент нечеткости равный длине носителя LL/RR - числа взятой с положительным (LL- число) или отрицательным (ДД-число) знаком; « Е [0; 1] - уровневые значения функции принадлежности.

LL/RR-числа получаются из исходной экспертной оценки числовой величины LR- типа, с треугольной функцией принадлежности, представленной триадой ( xL, m, xR ), с помощью выпуклой линейной комбинации, определяющего точку на « -интервале:

x ( « ) = L ( Х_а ) = AxL ( « ) + (1 — А ) xR ( « ) , А Е [0 , 1] .                (5)

Здесь А - управляющий параметр, значение которого определяется требуемыми свойствами решения задачи.

Операции S ₁ над нечеткими числами (4) выполняются по следующим правилам [9]:

x i ( « ) ф x^(« )= a i + a 2 + ( b i + b 2 ) «,                        (6)

x i ( « ) ® x 2 ( « ) = a 1 a 2 + ( a 1 b 2 + a 2 b 1 + b 1 b 2 ) «,                     (7)

x 1 ( а ) Ф (— x2(а )) — a 1 — a 2 + ( b 1 — b 2 ) a,   —x — —a — ba,            (8)

x 1 ( a ) ® x- 1 ( a ) — a 1 /a 2 + [( a 2 b 1 — a 1 b 2 ) / ( a 2 + a 2 b 2 )] a, ^b

x 1 ( a ) — a ¹--7---- —a, a — 0 , a — —b.

^v '            a ( a + b )

Так как в (6) - (9) операции линейны по переменной a, множество ^ является замкнутым по всем операциям, то есть если xi,xj E K, to xi * xj E K.

В работе [9] показано, что множество К с операциями (6) - (9) представляет собой алгебру модифицированных нечетких LL/RR-чисел с единственным нулевым элементом 0 — (0 + 0 a ) 11 единственным единичным числом 1 — 1 + 0 a.

Алгебра P — (K; S 1) позволяет применять операции независимо от расположения нечетких чисел на числовой оси, не допускает необоснованного расширения нечеткости, сохраняет треугольную форму нечеткого результата применения операций и естественные математические отношения в задаче, например, тождественность уравнения с нечеткими переменными понимается как равенство функций принадлежности левой и правой части уравнения.

Если по каким-либо причинам модификация нечетких чисел в LL/RR-44C3\a недопустима, то в работе [10] предлагается алгебру P — (K ; S 1 ) применять отдельно к левой и правой части нечеткого ЕЯ-числа с треугольной функцией принадлежности. При этом все свойства результатов операций, достигнутые в [9], сохраняются.

Реализация операций (6) - (9) отличается от реализации аналогичных операций над действительными числами, что не позволяет применять при решении задач стандартные программные пакеты.

• 2.    Построение подходящего изоморфизма и методики решения задач с нечеткими параметрами

Изоморфизмом алгебры P — (K ; S 1 ) на алгебру G — (M ; S ₂ ) будем называть отображение Г : K ^ M , удовлетворяющее условиям

Г( S 1 ( k )) — S 2 (Г( k )) , k E K.                           (10)

S 1 (Г - 1 ( m )) —Г - ¹ S 2 ( m )) , m E M.                       (11)

Необходимо подобрать такой изоморфизм Г, чтобы реализация алгебры G использовала операции над действительными числами и допускала применение стандартных программных пакетов для решения задач с нечеткими параметрами.

Пусть элементы множества M представлены в виде x(a) — x(0) + (x(1) — x(0))a, где x(0), x(1) - действительные числа. Сигнатура S2 определяется выражением x1 (a) * x2(a) — ax(1) + (1 — a)x(0) — x(0) + (x(1) — x(0))a,          (12)

где x (0) — x1 (0) * x ₂ (0); x (1) — x 1 (1) * x ₂ (1); * E { + , —, •, /} и все операции выполняются по правилам работы с действительными числами.

Предложение 1. Алгебры P и G изоморфны.

Для доказательства этого предложения рассмотрим элементы множеств M и K. Очевидно, что любой элемент множества K -x(a) — a + ba получается из элементов множества M простой подстановкой а = x(0), b = (x(1) — x(0)), в этом случае K = M, а отображение Г является отображением на себя. Множество K является замкнутым по операциям (6-9), поэтому для доказательства гомоморфизма (10) и обратного гомоморфизма (11) достаточно показать справедливость равенства S1(k) = S2(m). Поскольку результат операций в обеих алгебрах представляет собой линейную функцию от параметра а, достаточно показать, что эти результаты совпадают в двух точках, например, при а = 0 и а = 1. Совпадение результатов легко проверяется выполнением операций по правилам (6-9) и (12) для двух нечетких чисел а 1 + b । а а а2 + b2а.

Предложенный подход позволяет использовать стандартные программные пакеты для решения задач с нечеткими параметрами по следующей простой методике:

Шаг 1. Преобразовать нечеткие параметры задачи, заданные как треугольные нечеткие числа в модифицированные нечеткие числа (4) с помощью преобразования

(5). Для этого надо представить границы а -интервалов в виде (3), выбрать подходя

щее значение А для каждого нечеткого параметра, например А =

m - xL

x

R

-

x

L

обеспечи

вает минимальную потерю информации при переходе от LR -чисел к модифицированным ТТ//?/?-числам [9].

Шаг 2. Решить задачу с модифицированными нечеткими параметрами как задачу с четкими параметрами при а =1. Обозначить решение - x (1).

Шаг 3. Решить эту же задачу с параметрами, соответствующими а =0. Обозначить решение - x (0).

Шаг 4. Построить модифицированное нечеткое решение как линейную комбинацию решений x (1) и Д0):

х( а ) = x (0) + ( x (1) — x (0)) а.

Рассмотрим примеры решения задач с использованием предложенной методики. В качестве примеров рассмотрим задачи, приводящие к выбору решения в виде нечеткой точки (решение уравнения и задачу линейного программирования) и в виде функции с нечеткими параметрами (решение дифференциального уравнения).

Пример 1. Пусть эффективность некоторого производственного проекта описывается непрерывной функциональной зависимостью от изменения (увеличения или сокращения) объема выпуска товарной продукции - ж, и эта зависимость имеет экстремум. Один из параметров этой зависимости определяется экспертным путем в виде нечеткого числа. Допустим, что необходимое условие экстремума приводит к решению квадратного уравнения x ² + Bx + 2 = 0, г де B = (2; 3; 5).

Шаг 1. bL = 2 + а; bR = 5 — 2а. Пусть А выбирается из условия минимальных потерь экспертной информации, т.е. А=1/3. Тогда b(а) = 4 — а. Уравнение с модифицированным нечетким числом, которое предстоит решать, имеет вид x (а) + (4 — а)х(а) + 2 = 0.

Шаг 2. При а =1 решаем уравнение x ²( а ) + 3 х ( а ) +2 = 0. Пол учим Х1 (1) = ^{— 1} , ^x 2⁽¹⁾ = ^{— 2}

Шаг 3. При а =0 решаем уравнение x ²( а ) + 4 х ( а ) +2 = 0. Получим с точностью до двух знаков Х 1(1) = — 0 , 59 , x ₂(0) = — 3 , 41.

Шаг 4. Модифицированное нечеткое решение:

Х1 = - 0 , 59 - 0 , 41 а ; Х2 = - 3 , 41 + 1 , 41 а. (13)

Нетрудно проверить, что решение (13) при подстановке в уравнение Х 2 ( а ) + (4 — а ) х ( а ) + 2 = 0 превращает его в четкое тождество (в смысле равенства функций принадлежности).

Полученное решение можно интерпретировать как требование сокращения объема выпуска продукции на нечеткую величину, определяемую либо одним, либо другим нечетким интервалом (13), что обеспечит эффективность. В данном случае, выбор в произвольной точке одного из этих интервалов обеспечивает оптимальность со значением функции принадлежности равном соответствующему значению а. Выбор за пределами интервалов (13) не обеспечивает оптимальности решения.

Пример 2. Задача сетевого планирования проекта при нечетко заданных продолжительностях работ. Пусть дан проект, заданный табл. 1. Соответствующий сетевой граф показан на рис. 1.

Таблица 1

Операция	Предшествующие операции	Нечеткая операций, т			продолжительность
		τL	m	τR
А	—	1	2	5
В	—	2	4	5
С	А	3	7	9
D	В	4	6	9
Е	В	9	10	12
F	С	4	5	6
G	D, Е	1	5	6
Н	F, G	2	4	7

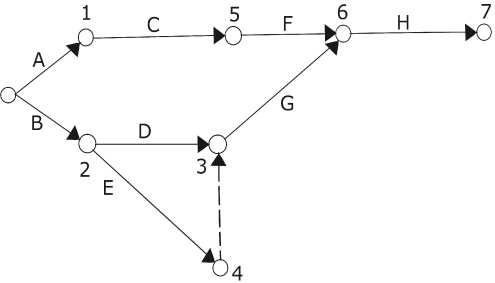
Рис. 1. Сетевой граф проекта

Требуется определить критические операции проекта и общее нечеткое время выполнения проекта. Примем для определенности единицу времени - дни.

Необходимое решение можно получить как решение задачи линейного программирования с нечеткими параметрами:

• tn - t о ^ min;

• tjs - tis > Ts, Vs = 1 ,.. 8; ^T = E ^Ts i ;

  
  

s 1

где t 0 , tn - моменты времени начала и окончания проекта; t_is, tjs - моменты начала и окончания s -й операции; Ts - нечеткая иродолжительность s -ой операции; Ts 1 - нечеткая продолжительность операций критического пути, т.е. операций для которых в результате решения выполняется равенство tjs 1 — tis 1 = Ts 1 (в смысле равенства функций принадлежности левой и правой части уравнения). Такие ограничения в задачах линейного программирования принято называть дефицитными ограничениями; T - продолжительность проекта.

Система неравенств в задаче (14) применительно к табл. 1 примет вид:

1 1 — t о >  Ta ( a );    1 2 — 1 0 > TB ( a );    1 5 — 1 1 > TC ( a );    1 3 — 1 2 > TD ( a );

• ¹ 4 ^{— 1} 2 > ^TE ^{( a} );    ¹ 6 ^{— 1} 5 > ^TF ^{( a} );   ¹ 6 ^{— 1} 4 > ^TG ^{( a} )i    ¹ 7 ^{— 1} 6 > ^TH ^{( a} ) •

Следует обратить внимание на то, что предложенная методика решения позволяет устранить проблему сравнения нечетких чисел в представленной системе неравенств, заменяя ее соответствующей системой сравнения действительных чисел. При решении следует предусмотреть фиктивную операцию, которой соответствует равенство 1 3 — 14 = 0.

Выполним необходимые шаги предложенной методики.

Шаг 1. Примем для всех нечетких чисел, определяющих продолжительность операций, параметр А =0,5. Соответствующие модифицированные числа примут вид:

TA ( a ) = 3 — a ; TB ( a ) = 3 , 5 + 0 , 5 a ; TC ( a ) = 6 + a ; TD ( a ) = 6 , 5 — 0 , 5 a ;

TE ( a ) = 10 , 5 — 0 , 5 a ; TF ( a ) = 5; TG ( a ) = 3 , 5 + 1 , 5 a ; TH ( a ) =4 , 5 — 0 , 5 a.

Задача (13) принимает модифицированный вид:

tn ( a ) — t ₀( a ) ^ min;

tjs ( a ) — tis ( a ) > Ts ( a ) ,   Vs = 1 ,..., 8;

T ( a ) = E Ts i ( a ) .

s 1

Шаг 2. Решаем детерминированную задачу линейного программирования (15) при a =l, например, с помощью электронных таблиц Excel. Решение будет иметь следующий вид:

t о (1) = 0; t i (1) = 7; t 2 (1) = 4; £ з (1) = 10; t 4 (1) = 14; ^(1) = 14; t 6 (1) = 19; £ 7 (1) = 23 .

Критические операции: В; Е; G; Н.

Продолжительность проекта: T (1) = 23 дня.

Шаг 3. При a =0 решение задачи (15) примет следующий вид:

t о (0) = 0; t i (0) = 7 , 5; t 2 (0) = 3 , 5; £ з (0) = 10; t 4 (0) = 14; t s (0) = 12 , 5; ^(0) = 17 , 5; t 7 (0) = 22 .

Критические операции: В; Е; G; Н.

Продолжительность проекта: т (0) = 22 дня.

Шаг 4. Модифицированное нечеткое решение задачи (15) будет включать нечеткие интервалы моментов времени начала и окончания операций проекта:

t₀(а ) = 0; t1(а ) = 7 , 5 — 0 , 5 а ; t₂(а ) = 3 , 5 + 0 , 5 а ; t₃(а ) = 10; t₄(а ) = 14;

t5(а ) = 12 , 5 + 1 , 5 а ; t₆( а ) = 17 , 5 + 1 , 5 а ; Д( а ) = 22 + а.

Критический путь проекта составляют операции В; Е; G; Н.

Результаты решения задачи (15) имеют естественную интерпретацию:

• -    значение критерия минимально по переменным ti ( а ) при всех значениях а ; при а =1 решение соответствует четкой задаче, мера отклонения от этого решения вправо или влево рассматривается как мера риска;

• -    сумма нечетких продолжительностей операций критического пути равна (в смысле равенства функций принадлежности) нечеткому моменту времени окончания проекта, то есть нечеткая продолжительность проекта определяется выражением т(а ) = 22 + а , т.е. возможно проект будет выполняться в интервале (22; 23) дня;

• -    общий резерв времени, например, операции А определяется выражением t 1( а ) — TA ( а ) = 4 , 5 + 0 , 5 а , которое характеризует риск сокращения резерва времени в интервале (4,5; 5) дней. У критических операций резерва времени нет, например, общий резерв времени операции В равен t ₂( а ) — TB ( а ) = 3 , 5 + 0 , 5 а — 3 , 5 — 0 , 5 а = 0.

Выполнение этих естественных соотношений подтверждает достоверность полученного решения.

Пример 3. В предыдущих примерах рассматривались нечеткие аналоги задач выбора, решением которых являются точки в п-мерном пространстве. Для того, чтобы проиллюстрировать нахождение решения в виде функции, будем рассматривать дифференциальное уравнение с нечеткими параметрами. Пусть имеется задача Коши с нечетким параметром

-y = Ay ;   A =( — 2; 0; 1);

y ( t = 0) = 1 .

Найдем частное решение этого уравнения, следуя предложенной методике.

Шаг 1. Примем параметр А =0,5. Модифицированное представление нечеткого параметра уравнения (16) примет вид: 0( а ) = — 0 , 5 — 0 , 5 а. Модифицированное представление дифференциального уравнения:

dyO- = ( — 0 , 5 — 0 , 5 а ) С(а ); y(a, t = 0) = 1 .

Шаг 2. Решим уравнение (17) при а =1:

dy ⁽¹⁾ = ^{—у (1);}

y (1 , t = 0) = 1 .

Решение: y(1) = exp( —t ).

Шаг 3. Решим уравнение (17) при а =0:

= - 0 , 5 5(0);

Ц0 , t = 0) = 1 .

Решение: у (0) = exp( — 0 , 5 1 ).

Шаг 4. Модифицированное нечеткое частное решение уравнения (17) представляет собой линейную комбинацию решений шагов 2 и 3:

у ( а ) = exp( — 0 , 5 1 ) + (exp( —t ) — exp( — 0 , 5 1 )) а.                  (18)

Подстановка решения (18) в уравнение (17) дает четкое тождество. Решение (18) представляет собой семейство экспонент (рис. 2), непрерывно зависящее от параметра а Е [0; 1]. Решение (18) будет устойчивым по Ляпунову для всех значений а.

Рис. 2. Устойчивое решение задачи Коши с нечеткими параметрами

В примере 3 решение имеет вид выпуклой линейной комбинации решений при а Е { 0 , 1 } также как и в примерах 1 и 2, но является не нечетким числом, а нечеткой функцией двух переменных. В общем случае решение как модифицированная нечеткая функция будет иметь вид: у( t, а ) = a ( t ) + b ( t ) а, а при фиксированном значении t нечеткое значение функции примет вид модифицированного нечеткого числа (4). Следует обратить внимание на зависимость коэффициента нечеткости b ( t ) (длины носителя модифицированного нечеткого числа) от переменной t и уменьшении этого коэффициента с ростом t для устойчивых по Ляпунову решений.

3. Исследование проблемы устойчивости решения

Замкнутости множества ^относительно операций в алгебре модифицированных нечетких чисел недостаточно для построения интерпретируемого решения задач с нечеткими параметрами. Если процедуру построения решения некоторой произвольной задачи обозначить как оператор х( а) = Ф( x; а( а)), г де й( а) Е K, то возникает вопрос - будет ли решение х(а) Е K? То есть, будет ли нечеткое решение, полученное по предложенной методике, представимо как модифицированное нечеткое число? Подобные вопросы впервые рассматривались в работах [11, 12], применительно к задаче линейного программирования с приближенно заданными параметрами. Небольшие изменения решения как результат небольших изменений параметров в этих работах определялось как устойчивость решения. По аналогии свойство сохранения решением вида (4) будем называть устойчивостью решения.

Обсуждение проблемы устойчивости удобно начать с примеров.

Пример 1*. Вернемся к примеру 1 и введем новую нечеткую оценку параметра B = (1; 2; 5). Тогда, для квадратиого уравнения x ² + Bx + 2 = 0. а, точнее его модифицированного аналога, полученного при А =0,5 и имеющего вид x ²( а ) + (3 — а ) х( а )+2 = 0 пр и а = 1, решения не существует на множестве действительных чисел. При а =0 решение существует: Х 1 (0) = — 0 , 666 и Х ₂(0) = — 3. Нетрудно проверить, что в точке а ~ 0 , 15 функция нечеткого решения имеет разрыв. По одну сторону от этой точки имеется непрерывное решение, по другую - решение отсутствует. Очевидно, что в этом случае предложенный метод получения решения, основанный на линейной аппроксимации по границам а -интервалов, не применим.

Пример 2*. Похожая ситуация может возникнуть и в примере 2. Поменяем параметры у операций Е и F в табл. 1 так, как это показано в табл. 2:

Таблица 2

Операция	Предшествую щие операции	Нечеткая    продолжитель ность операций, т
		τL	m	τR
А		1	2	5
В		2	4	5
С	А	3	7	9
D	В	4	6	9
Е	В	6	7	9
F	С	4	5	12
G	D, Е	1	5	6
Н	F, G	2	4	7

Пусть также как и в примере 2 параметр А для всех операций будет равен 0,5. Но теперь нечеткое решение в виде ti ( а ) , i = 0; 1; ... ; 7 , а также зависимость продолжительности проекта от параметра а уже не являются непрерывными функциями. В этом легко убедиться, рассмотрев, например, оптимальное значение критерия задачи (14) в точках а Е [0; 0 , 25; 0 , 5; 0 , 75; 1], представленное в табл. 3.

Таблица 3

	Значение минимизируемого критерия	Критический путь
а =0	21,5	ACFH
а =0,25	20,625	ACFH
а =0,5	19,75	ACFH
а =0,75	19,75	BEGH
а =1	20,0	BEGH

При а Е [0; 0, 5] функция изменяется линей:ю. На промежутке значений а от 0.5 до 0,75 функция решения имеет разрыв, так как критический путь изменяется на кон- цах этого промежутка. Этот разрыв уже не позволяет интерпретировать результаты решения как в примере 2.

Примеры 1* и 2* показывают, как решение на промежутке изменения значений а теряют треугольную форму, что рассматривается как неустойчивость решений соответствующих задач. Можно утверждать, что решение большинства задач с нечеткими параметрами с помощью предложенной методики имеет интерпретируемый смысл только при условии устойчивости этого решения. В этой связи для практического использования предложенной методики актуально наличие простых, легко проверяемых условий устойчивости. С этой целью для решения в виде нечеткого числа или вектора нечетких чисел можно дать следующее определение устойчивости.

Определение 1. Задача F ( а(а ) , x ) = 0_; содержащая параметры, значения которых заданы нечеткими промежутками ai = [ ai (0); ai (1)]_; i = 1 , ...,n ; устойчива но решению, если:

• -    она имеет решение для всех значений параметров a 6 01 х ... х 0 ^;

• -    для любого заданного е >  0 найдется 5 ( е >  0) такое, что при выполнении условия |а 1 — а2| <5, для всех а 6 [0; 1]_; выполняется условие - для всех компонент x ( а ) решения задачи lx ( а ₁) — x ( а2 ) | <  е (рис. 3).

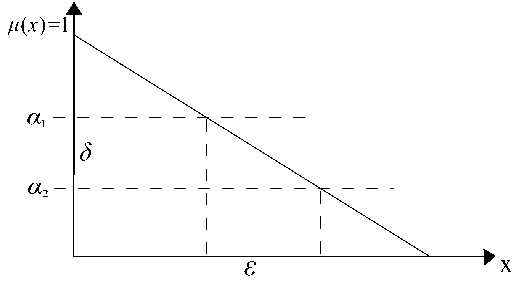
Рис. 3. Иллюстрация к определению устойчивости

Иными словами, необходимым условием устойчивости является непрерывность решения как функции параметра а. Определение устойчивости по решению задачи с нечеткими модифицируемыми параметрами или просто устойчивости нечеткого модифицированного решения можно сформулировать в следующем эквивалентном виде.

Определение 2. Задача F ( а(а ) , x ) = 0 имеет устойчивое решение если:

• -    она имеет решение для всех значений параметров на всех а-уровнях при а 6 [0; 1];

• -    каждая компонента x(а)решения непрерывная функция на промежутке а 6 [0; 1].

Для некоторых задач удается сформулировать практически значимые условия устойчивости, легко проверяемые в процессе вычислений. Так для типов задач, рассматриваемых в примерах 1* и 2*, эти условия можно сформулировать следующим образом.

Предложение 2. Для того чтобы нечеткое модифицированное решение х(а ) = x (0) + ( x (1) — x (0)) а квадратного уравнения а( а ) x ²+ b ( а ) x +с( а ) = 0 било устойчивым, достаточно существования решений x (0) , x (1).

Доказательство этого утверждения следует из простых рассуждений. Если существуют решения x(0), x(1), то необходимо следует существование неотрицательного дискриминанта D (а) = b 2( а) — 4 а( а) A (а) пр и а = 0 и а=1. Но в силу линейности операций (6) дискриминант - монотонная функция параметра а. Значит из выполнения неравенств D(0) > 0 i1 D(1) > 0 еле.тует D(а) > 0 при всех а Е [0; 1]. что п является достаточным условием^ существования решений на всех «-уровнях.

_        —b ( а ) i ( D ( а )) 0 ^{, 5}

Решение х ( а ) = ------——------ пепрерывттая функция на промежутке а Е

2 a ( а )

[0; 1] и D ( а ) >  0 в силу линейности операций (6) - (9). Полученные результаты полностью соответствуют определению 2, что и доказывает утверждение 2.

Предложение 3. Нечеткое модифицированное решение xi ( а ) = xi (0) + ( xi (1) — xi (0)) a ; i = 1 , ...,n задачи линейного программирования канонического типа с нечеткими параметрами

£ aixi ^ min;

i =1

^£ bijxi = с j ( а ); j = 1 , ...m ; m < n ;

i =1

будет устойчивым, если существуют оптимальные решения x (0) , x (1), полученные для одной группы базисных переменных, т.е. принадлеэюащие одноименным вершинам выпуклых многогранников допустимых решений, образованных равенствами £ bijxi = с j (0) гi £ bijxi = с j (1).

ii

Действительно, если решения x (0) = ( x 1 (0); ... ; x_n (0), x (1) = ( x 1 (1); ... ; x_n (1)) существуют и принадлежат одноименным вершинам, то им соответствуют две системы уравнений относительно базисных переменных xi, i = 1 , ...,m

m

£ bij xi = i=1

m

£ bij xi = i=1

-

-

n

£ bijxi + Aj (0), j = 1, i=m +1

n

£ bij xi + с j (1) , j = 1 ,. i = m +1

..., m ;

..., m.

А 1 (0)

Представим решения этих уравнении в виде x (0) = (— а—

; ... ;

(АШ

( А ;

. ;

А n (0)

-"A^-) 11 x ⁽¹⁾ =

^А n ⁽¹⁾

—А—) где символом А обозначены определители правила Крамера. При

этом А = 0. Следователь но, для всех а Е [0; 1] будут существовать решения x ( а ) =

^А 1 ⁽ a ) ⁽ А ^;

. ;

—А ^ )• Непрерывность компонент вектора решения x ( а )обусловлена ли-

нейностью операций (6) - (9). Поскольку каноническая форма задачи линейного программирования сводится к стандартной и общей форме, утверждение справедливо и для этих представлений задачи.

Перейдем к рассмотрению проблемы устойчивости для решения дифференциального уравнения с нечеткими параметрами и рассмотрим пример.

Пример 3*. В примере 3 изменим нечеткий параметр следующим образом: A = ( — 1; 0; 1 , 6).                                                                     _y

Уравнение с модифицированным параметром ( А =0,5) ^dyd|⁾ = (0 , 3 — 0 , 3 а )у( а ).

dy ⁽¹⁾

Дифференциальные уравнения при а =1 и а =0 примут вид: —-— dt

= 0, dt

• 0 , 3у( а ). Соответствующие решения будут иметь вид: у(1) = 1 и y(0) = exp(0 , 3 t ). Очевидно, что первое решение устойчивое, второе не устойчивое по Ляпунову по переменной t. Сформируем частное решение в виде выпуклой линейной комбинации решений (рис. 4), полученных при а =1 и а =0, получим неустойчивое решение в виде нечеткой функции: у ( t, а ) = exp(0 , 3 t ) + (1 — exp(0 , 3 t )) а.

  

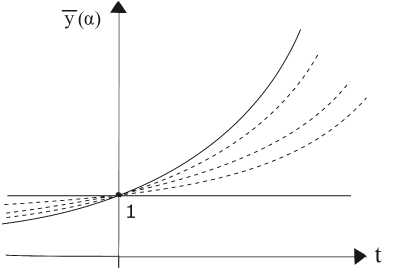
  Рис. 4. Неустойчивое решение задачи Коши с нечеткими параметрами

  
  

Подставив это решение в исходное уравнение, можно убедиться в тождественном равенстве функций принадлежности левой и правой частей уравнения. Следует обратить внимание на неограниченный рост коэффициента нечеткости решения с увеличением t для неустойчивого по Ляпунову решения. При этом, несмотря на то, что формально треугольная форма численного значения решения сохраняется при всех значениях t , нечеткое решение становится не пригодным для практического использования, а, следовательно, построение выпуклой линейной комбинации решений, полученных при а =1 и а =0, не имеет смысла.

Определение 3. Задача Коши dy = У( а ) у, с начальными условиями y ( t = 0) = у о, содержащая параметр, значения которого заданы нечетким промежутком ai = [ Уi (0); Уi (1)]_; i = 1 , ...,n ; устойчива по решению, если:

—

—

она имеет решение для всех значений параметра а(а ) , а Е [0; 1];

для любого заданного е > 0 найдется 5(е) > 0 такое, что при выполнении условия |а 1 — а21 < 5, для всех а Е [0; 1] и всех значений t, выполняется условие ly(t, а 1) — у(t, а2) | < е, где у(t, а) - решение задачи.

Предложение 4. Задача Коши, сформулированная в определении 3, будет иметь устойчивое решение, если будут существовать устойчивые по Ляпунову решения этой задачи при а=1 и а=0.

Это предложение достаточно очевидно, так как линейная форма нечеткого числа позволяет сохранить условия существования решения внутри промежутка [0; 1], если существуют решения при а=1 и а=0, а устойчивость этих решений по Ляпунову обеспечит выполнение второго условия определения 3.

Заключение

В результате проведенных исследований получена обоснованная методика решения ряда задач выбора и управления, представленных моделями с параметрической нечеткостью. Методика состоит из следующих этапов:

• 1.    В рассматриваемой модели каждый нечеткий параметр, заданный как нечеткое число ТУ?-типа представляется в виде совокупности а -уровневых интервалов в соответствии с (2).

• 2.    К границам интервалов применяется выпуклое линейное преобразование (5) с фиксированными параметрами X, в результате чего нечеткие параметры приобретают вид модифицированных нечетких чисел LL/RR-типа (4), отражающих основные, с точки зрения выбора, характеристики нечеткости.

• 3.    В исходной модели нечеткие параметры переписываются в виде модифицированных чисел, и задача решается для границ промежутка изменения значений а Е { 0; 1 } , как обычная задача с четкими параметрами. В результате получается два четких решения.

• 4.    Полученные решения анализируются на устойчивость, и делается вывод о возможности построения модифицированного нечеткого решения задачи.

• 5.    Модифицированное решение строится как выпуклая линейная комбинация полученных в п. 3 четких решений и представляет собой линейную аппроксимацию решения исходной задачи.

Предложенная методика обеспечивает процесс получения решения:

• -    с ограниченным расширением неопределенности, обусловленным применяемой для вычислений алгеброй;

• -    допускающего естественную интерпретацию промежуточных и конечных результатов, прежде всего, за счет сохранения треугольной формы представления нечеткости при выполнении различных операций над нечеткими числами;

• -    позволяющий производить обработку нечеткой информации с помощью стандартных программных пакетов, работающих с действительными числами, что существенно упрощает расчеты.

Достоверность методики подтверждается при решении уравнений их тождественностью при подстановке нечеткого результата, а при решении задачи линейного программирования сохранением естественных отношений между компонентами нечетких решений. Это исключает необходимость сравнения предложенной методики с известными аналогами, которые не обеспечивают указанные свойства решений в принципе.

Работа выполнена при финансовой поддерэюке гранта РФФИ № 13-08-00532.