Анализ информации о регулярном характере структуры снежной лавины на основе выявления почти периодов

С развитием современного туризма и горной промышленности возникает вопрос исследования опасных природных явлений на примере лавин с целью прогнозирования зон ущерба и противодействия их разрушительной силе. Согласно определению, снежные лавины представляют собой массы снега, падающие или движущиеся со скоростью 20–30 м/с. Явление распространено как на территории России [1, 2], так и за границей – например, в Казахстане [3–5] и Турции [6].

Для исследования применяются различные методы и модели – так модель RAMMS демонстрирует удовлетворительные результаты даже в условиях недостатка данных [7, 8]. При этом существенную роль в анализе сыграло зонирование по степеням опасности. Таким образом, вопрос о структурной сегментации лавины показывает свою актуальность в целях улучшения качества прогнозных моделей.

Одним из универсальных методов анализа данных, обладающих упорядоченным аргументом – будь то пространство или время, – является почти периодический анализ [9].

Известно, что метод применим для пространственного сегментирования опасных природных явлений [10, 11]. В работе предлагается оценка системного характера структуры лавины на основе почти периодических характеристик явления.

Описание данных . Исследование проводится на графическом изображении лавины, сошедшей 11 января 2025 года в Альпах на хребте между французской коммуной Ларш (Larche)

Крынецкий Б.А., Калач А.В., Анализ информации о регулярном характере структуры Парамонов А.А. снежной лавины на основе выявления почти периодов и итальянским населенным пунктом Саретто (Saretto) в коммуне Аччельо (Acceglio), взятом с открытого Интернет источника [12].

Лавина сошла слоем толщиной в 15–30 см по поверхности грунта. Критических последствий схода лавины, к счастью, нет – на пути спуска не находились объекты инфраструктуры или туристические группы. Изображение приводится к черно-белой гамме, а для дальнейшего анализа обрабатывается в представлении в виде матрицы, элементы которой описывают интенсивность белого цвета в пикселе строки и столбца приведенного изображения.

Описание методов . Для проведения структурной сегментации лавины в исследовании предлагается применение почти периодического анализа в структуре лавины. Для этого необходимо привести область изображения к спрямлённому виду для представления структуры лавины в виде наборов данных с упорядоченным аргументом.

Преобразование данных основывается на алгоритме полигональной трансформации. В пространстве исходного изображения создаётся сеть узлов полигонов, сопряженных в форме цепочки, описывающей область исследуемого явления. Внутри полигонов с заданными частотами определяются сетки узлов дискретизации преобразованных данных. Для линеаризации выбраны частоты продольной и поперечной дискретизации – 600 и 300 узлов соответственно. Спрямленный набор данных в виде набора горизонтальных и вертикальных срезов – последовательностей упорядоченных по аргументу значений яркости узла дискретизации подвергали почти периодическому анализу для определения существования и синхронизации систем ритмичных тактов в срезах, что позволит провести структурную сегментацию линеаризованного набора и воспроизвести разметку существенных границ в теле исследуемой лавины.

Почти периодический анализ определяет значения, близкие по определению к периоду функции, на основе обобщённой сдвиговой функции – синтезированной из сдвиговой функции и анаморфозы данных, выделяющей колебательную компоненту из единой с трендом структуры.

Исследование почти периодов по различным срезам позволяет систематизировать наблюдения и выявить наиболее существенные характеристики, описывающие данные. Так, рассмотрение ритмичных компонент по поперечному срезу в середине линеаризации приводит к исследованию локальных минимумов сечения обобщенной сдвиговой функции.

Установлено, что анализируемая система локальных минимумов представляет практически идеальную алгебраическую последовательность, что указывает на их фундаментальный характер. Отдельного упоминания заслуживает почти период в 87 узлов дискретизации – он имеет самое малое значение обобщенной сдвиговой функции во всей системе.

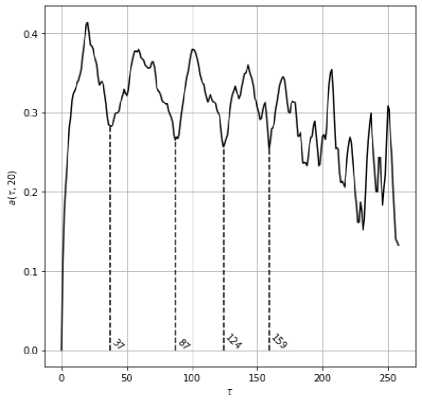
Рис. 1. Сечение обобщенной сдвиговой функции для 250-о поперечного среза линеаризованных данных с разметкой системы локальных минимумов

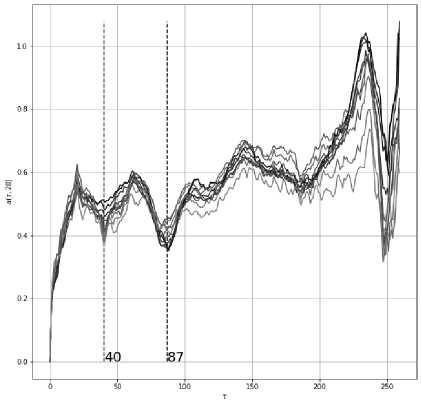
Рис. 2. Сечения обобщенной сдвиговой функции для системы поперечных срезов линеаризованных данных с разметкой системы локальных минимумов

Математика

Для первичной систематизации проведем почти периодический анализ для поперечного сечения линеаризованных данных в 400-й вертикали. Система почти периодов на данном срезе также носит ритмичный характер алгебраической последовательности с шагом, близким к 30 узлам дискретизации. Отдельно необходимо отметить то, что почти период в 87 узлов дискретизации встречается в обеих системах локальных минимумов, что существенно выделяет его и наделяет уже системным характером. Чистое воспроизведение почти периода в 87 узлов дискретизации встречается и в системе локальных минимумов для 250-го вертикального сечения линеаризованных данных, приведенной на рис. 1.

Установлено, что если провести почти периодический анализ в системе первого десятка вертикальных срезов, то система сечений обобщенной сдвиговой функции показывает единообразное поведение (рис. 2).

Рис. 2 убедительно демонстрирует существование пары практически кратных почти периодов в 40 и 87 узлов дискретизации. Также наблюдается подобие локального минимума в окрестностях 185 узлов дискретизации и существенного локального минимума при 250 узлах дискретизации, однако слабая обеспеченность данными позволяет пренебрегать последней четвертью среза. Таким образом, в структуре почти периодов поперечных сечений линеаризованных данных тактовый интервал в 87 узлов дискретизации демонстрирует систематический характер, претендуя на статус фундаментальной составляющей исследуемого явления.

Проведение почти периодического анализа в системе горизонтальных сечений линеаризованных данных позволит оценить продольные почти периоды в структуре. Так, для серединного продольного сечения срез обобщённой сдвиговой функции показывает, что существенные локальные минимумы так же, как и в исследованиях поперечных почти периодов образуют последовательность, схожую с арифметической прогрессией. Помимо существенных локальных минимумов существенно выделяется система ритмичных высокочастотных оврагов, указывающая на неявный фундаментальный малый почти период примерно в 12 узлов дискретизации, однако относительная глубина соответствующего прогиба невелика.

Проведение почти периодического анализа для другого горизонтального среза линеаризованных данных даёт систему ритмичных тактов, в которых явление почти периода в 12 узлов дискретизации носит более явный характер. Его можно зафиксировать в виде последовательности локальных минимумов в 12, 24, 36 и 50 (близко к 48) узлах дискретизации, а существенные локальные минимумы соответствуют 100, 155 и 235 узлам дискретизации.

Особенности полученных срезов обобщенной сдвиговой функции для горизонтальных сечений линеаризованных выражены обилием локальных минимумов, образующих почти строгие алгебраические последовательности с фундаментальным почти периодом в 12 узлов дискретизации. Также можно выделить существенные минимумы, соответствующие трендовому углублению графика среза в 155 и 305 узлах дискретизации.

Таким образом, почти периодический анализ показал системный

Рис. 3. Комбинации композиций продольных и поперечных почти периодов на исходных данных

характер некоторых тактов развития структуры лавины в продольном и поперечном направлениях.

Возникает возможность визуализации структурной сегментации, основан-

Крынецкий Б.А., Калач А.В., Анализ информации о регулярном характере структуры Парамонов А.А. снежной лавины на основе выявления почти периодов ной на определённых регулярных почти периодах. Для демонстрации на рис. 3 рассматриваются композиции продольных почти периодов в 155 и 305 узлов дискретизации и поперечных почти периодов в 40 и 87 узлов дискретизации.

Ритмичные границы приведённой сетки на исходных данных воспроизведены на рис. 3: белые линии определяют поперечные почти периоды, а чёрные - продольные почти периоды соответственно.

На рис. 3 видно, что в строках сохраняется величина поперечного почти периода - так, рис. 3, а и в имеют ширину синей сетки в 40 узлов дискретизации, а рис. 3, б и г - ширину синей сетки в 87 узлов дискретизации. Для ширины продольных почти периодов это правило сохранено внутри столбцов - рис. 3, а и б размечены красными границами с шагом в 155 узлов дискретизации, а рис. 3, в и г - 305 узлов дискретизации соответственно.

На рис. 3, б можно отметить удачную композицию почти периодов, формирующих структуризацию: отдельные области разграничиваются практически по идеальным цветовым сегментам - то есть высветленные области «турбулентного» характера строго отсекаются границами и по продольным, и по поперечным границам.

Рис. 3 показывает, что поперечный почти период в 87 узлов дискретизации делит снежную лавину на три продольные полосы - соответствующие условным трём зонам схода лавины, сошедшей от 2 линий, которые объединились в середине.

Продольный почти период в 305 узлов дискретизации отделяет область начала и развития схода лавины от зоны торможения и окончания пути лавины.

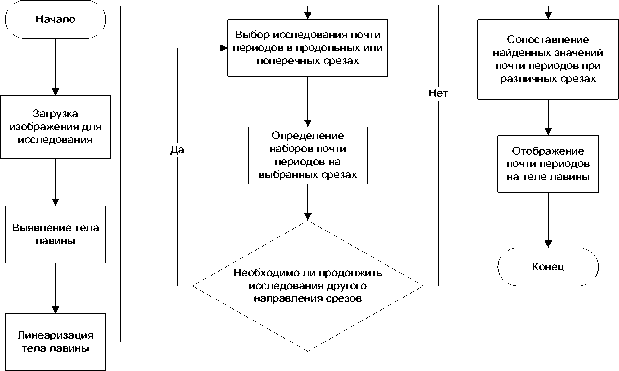
Рис. 4. Схема алгоритма анализа информации о регулярном характере структуры снежной лавины на основе выявленных почти периодов

На рис. 4 представлена общая схема алгоритма анализа информации о регулярном характере структуры снежной лавины на основе выявленных почти периодов.

Предложенная схема формирует основу для дальнейшего развития исследований пространственных структур лавин на основе почти периодического анализа.

Выводы

В рамках проведения исследования изображение структуры снежной лавины подвергалась спрямлению с использованием полигональной трансформации для дальнейшего почти периодического анализа снежного потока. Почти периодический анализ позволил установить существование в структуре снежной массы поперечных и продольных ритмичных интервалов развития лавины. Выявленные почти периоды показали системный характер - так, поперечный почти период в 87 узлов дискретизации был устойчиво обнаружен в большом наборе разрозненных срезов. Это указывает на его фундаментальный характер в вопросе описания структуры исследуемой лавины. Полученные результаты показывают единство ритмов структуры развития лавины, что указывает на существенные возможности к пространственной сегментации явления на основе применяемой методики анализа. Проработанный подход может быть интегрирован в системы по мониторингу и прогнозированию лавинной активности в целях поддержки принятия решений по совершенствованию мер обеспечения безопасности и профилактики чрезвычайных ситуаций.

Математика