Анализ инвариантности относительно преобразования Галилея двухфазных математических моделей гетерогенных сред

Перспективное использование взрывных процессов в ряде отраслей современной техники тесно связано с решением вопросов обеспечения мер безопасности, защиты инженерных сооружений и технологического оборудования от действия ударных волн (УВ). В связи с этим важное прикладное значение представляет изучение проблемы локализации механических эффектов взрыва и ослабления УВ с помощью математического моделирования данных физических процессов.

В настоящее время на практике ослабление УВ в газе осуществляется путем применения различных экранирующих систем в виде сплошных, перфорированных и разрушающихся перемычек. Один из основных недостатков сплошных и перфорированных перемычек состоит в их весьма большой материалоемкости и, соответственно, большой величине объемного содержания α твердого конденсированного вещества ( α ≈ 1 ÷ 0,1). Указанный недостаток в меньшей степени относится к перемычкам, разрушающимся при взаимодействии с УВ и образующим экранирующие слои или завесы из пены или аэровзвесей [1]. Поэтому с особой остротой встает проблема разработки математических моделей многокомпонентных гетерогенных сред [2], адекватных тем физическим процессам, которые они пытаются описывать. Более того, для быстропротекающих процессов есть такие проблемы, когда математическое моделирование является единственным средством предварительного изучения явлений [3, 4]. Для верификации расчетов, с одной стороны, используют известные экспериментальные данные, а с другой стороны, при анализе проведенных измерений используют математические модели. Очень важно, чтобы условия проведения расчетов и экспериментов совпадали, а математическая модель была адекватна изучаемому физическому процессу [5, 6].

В настоящей статье на примере анализа инвариантности относительно преобразования Галилея математической модели аэровзвеси [7], применяемой для математического моделирования перехода конвективного горения унитарного твердого топлива во взрыв, покажем, к чему может привести ситуация, когда расчеты и эксперимент проведены в разных системах координат.

Постановка задачи и математическая модель

Рассмотрим математическую модель течения газа с твердыми частицами (аэровзвесь), которая описывается системой уравнений сохранения [7], и проведем оценку ее на инвариантности относительно преобразования Галилея.

Система уравнений сохранения двухфазной аэровзвеси [7] имеет следующий вид

d t     dx’

^Pl + dpvl _ — J d t

dn d n— . — +--2 = 0, d t dx (3) dP1 V1 . dP1—12     dp_ +      + a = j + j—^, d t      dx      1 dx    j г (4) dp2V2 , dp2V22 , 3 „ dp _ г   к, +       + a^   = j jv^ , d t       dx     2 2 dx  j г (5) dp2 e2 + dp2 e2 V 2 = / q, T2 < TS d t       dx     [ Je 2, T2 > TS ’ (6) d(pEi + P2 Еэ)   d г r            , 14 22 +-. [P1V1E1 + P2V2E2 + (a1 V1 + a2v2)p] = 0, d t         dx (7) p     Px RT e1 = cp (T1 T0) o , p = д 0, P1       1- eP1 (8) 2 e2 = c 2(T2 - T0) + Q ° - p^, Ei= e+ -i-, P2            1 (9) P1 = P1°a1, P2 = P20a2, P20 = const, (10) q = nnd^Nu(T -T2),                                     (11)

f = n ro d ^{2 p C} _d ⁽ - ^{- —} 2 ) ^{- -} v 2I/ ^8,                                 (12)

(p.

J = n nd ² p ₂ u s — I .                                      (13)

I P 0 )

Здесь индексы 1, 2 относятся соответственно к газу и частицам; p i , a i ( i = 1,2) - истинные плотности и объемные содержания фаз; p i ,v i , T 1 ,e i , E i - парциальная плотность, скорость, темпе

ратура, внутренняя и полная энергия i -ой фазы; Q° - теплота химической реакции при

T ₂ = T ₀, p = p ₀; p - давление, n - число частиц в единице объема смеси; в - ковольюм; c_p и c ₂ - теплоемкости фаз; Д - теплопроводность газовой фазы; R 1 - универсальная газовая постоян-

ная; C_d и Nu – коэффициент трения и число Нуссельта, определяемые числами Рейнольдса ( Re )

и Прандтля ( Pr ) относительного движения фаз; d - диаметр частиц, u s и ф - эмпирические константы, характеризующие скорость горения топлива. Уравнения (1)–(3) – уравнения неразрывности газа и частиц и уравнение сохранения числа частиц в единице объема смеси; (4)–(5) – уравнения импульса газа и частиц; (6)–(9) – уравнения энергии частиц и смеси в целом; (8)–(10) – уравнения состояния; (11)–(13) – уравнения, определяющие члены теплового ( q ), силового ( f )

и массового ( J ) взаимодействия между фазами соответственно. Запишем исходную систему уравнений в новой системе координат, движущейся с постоянной скоростью D . Скорости в новой системе координат будут равны:

^- 1 н = ^V 1 ⁺ D , (14)

^V 2 н = ^V 2 ⁺ D ,

Координата будет определяться из уравнения: x„ = x + Dt , н

Производные:

d d

d x d x„ н

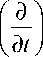
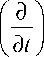
Г d )

( dХн )

D .

Таким образом, уравнение (1) с учетом (14)–(18) принимает вид:

Математика

dPl + dp) D + dA( Vi н - D) dt dxd нн или dPl , dPl D , dPl vi н p D = J

Эt   Эx„      Эx„Э ннн

Получаем:

dPi + dpi Vi н = J dtd

н

Аналогично, уравнения (2) и (3) с учетом (14)–(18) принимают вид:

^P^ + dp2 V 2 н = - J dtd

н dn d nv-.

— +--— = 0. dtd

н

Запишем уравнение (4) в новой системе координат:

"pl ^ - D)  p: 11 н - D) D . dp ' 1 н - D' + «Л = -f + J (v2 н - D), dt            Эx„               Эx„Э или dpi Vi н dpi D dpi Vi н D dpi D ----1----

dt      dt       dx„       dx„ нн

¹² d p V _H ²

J / i i н dx„ н

-

dpV, D dpD2     dp„

2 ' ’ ' ^н +  + «i^- = - f + J ( v 2 н - D ).

ОХ„      Оx„о ннн

Используя (19) получаем:

^d P i ^V i н d P i ^V i н ². „5 p_

1+ a = - f + JV^ .

dt       dx„       1 dxH     j 2 н нн

Аналогично, получается уравнение (5) с учетом (20):

^d A ¹ 2 н , ^d P 2 ¹ 2 н ²

d t

Рассмотрим уравнение (6): ^{d p} 2 ^e 2

d x„ н

3   d p

⁺ 7k ^a 2 3--= f ^- J^V 2 н .

^{2    d Х} н

или

+ ^{d p} 2 ^e 2

d t       d x„

н

D + d p 2 e 2 ( V 2 н - D ) = I q , T 2 <  T S

d x„ н

Je 2 , T >  Ts

d t      d x„

н

Откуда получаем:

^{d p} 2 ^e 2 + ^{d p} 2 ^e 2 D + ^{d p} 2 e 2 ^V 2 н

d x„ н

^{d p} 2 e 2 + ^{d p} 2 e 2 ^V 2 н =

d t

d x„ н

-

dp2 e2 D = I q, T2 < Ts dХн     [ Je2, T2 > Ts

q , T 2 <  Ts

Je 2 , T 2 >  Ts

.

.

Рассмотрим уравнение энергии (7), учитывая (14)–(21):

^d P i e i ⁺ к к

( v _{1 н}

D )²

к

⁺ P 2 e 2 ⁺

( V 2 н - D )² )

у" P i ^{( V} i. d x

н

(

D ) e к

d t

к

+

d p i e i ⁺ к к

( v i н - D ) 2 )

2 J

+ p ₂ e ₂ + к

( V 2 н — D )

d x„ н

D +

+ ( v i^- D )² J

²     7

к

^{+ p} 2 ^{( V} 2 н ^- D ) e 2 ⁺

к

( V 2 н — D ) 2 ^

^{+ ( a} i ⁽ V i н 7

^- D ) ^{+ a} 2^{( V} 2 н ^- D )) P ] = 0.

Раскрывая скобки, получаем:

d p i e i + 1 d p i ⁽ V i н ^- D ⁾² + d p 2 e 2 + 1 d p 2 ⁽ V 2 н ^- D ⁾²

d t    2       d t

d t     2        d t

+ dpieiD +1 dpiD(Viн - D)2 + dx„    2      dx„ нн

, dP2e2D , 1 dP2(v2н -D)2 , dpevн , 1 Эд vн(vн -D)2 др e D +111 дx„     2      дx„          дx„     2       дx„д н    нн    нн

1 ^d P 1 D ⁽ v l н ^- D ) ² . ^d P 2 e 2 v 2 н . 1 ^d P 2 v 2 н ⁽ v 2 н ^- D ) 2 ^d P 2 e 2 D 11

2      дx„           дx„     2       дx„д нн   нн

- 1 ^д Р 2 D ⁽ v 2 н ^- D ) 2 + d « 1 p ( v 1 „_Z D ) + ^{д а} 2 P ⁽ v 2 н ^- D ) = 0

д x„ н

д x„ н

д x„ н

После алгебраических преобразований получаем:

f V 2 ^ dP1 e1 + -y- к 2 д t

- D

др 2 1 e 2 + / '

к 2 7 д t dP\ V1 н + dP1 V1 н

-^ +

₊ D ² f ^d P 1 I ^д Р 1 v 1 н ) ₊ D ² f д р 2 ₊ ^д Р 2 v 2 н

д t    д x

н

I д t        д x„

н

+ а/ дXн )

- D

I fe+

^d P 1 v 1 н

D    d p

+ —а ~^— +----

2 ² d x„

н

² e 1 + v 1T к ² 7 d x„ н

+

к д t f     v. 2 ^

dP2 v 2 н e2 + -kf- к 2

d x„ н

^dp 2 v 2 н ^{д x} н

д t     д x

н

3    д p

⁺ а^у_л

^{2    д X} н )

+

д

- ⁺     [ ( ^a 1 v н ⁺ « 2 v 2 н ) P ^] = 0.

^{д X} н

Согласно (19) и (20) сумма третьего и четвертого слагаемых обращается в ноль, а пятое и шестое слагаемые согласно (22) и (23) будут равны (Df - DJv2н) и -(Df + DJv2н). В результате получим:

д ( P i E i„ + р ₂ E ₂„ ) д                                           D    д p

--------------⁺ 3" [ Р 1 ^v 1 н E 1 н ⁺ Р 2 ^V 2 н E 2 н ^{+ ( а} 1 ^V 1 н ⁺ « 2 ^V 2 н ) P ] ⁺ ^« 2^" = ⁰ •             (25)

д t          д x                                            2     д x„

В новой системе координат в уравнении полной энергии смеси (25) появился дополнительный член

D дp а2-^, 2 дxH н который приводит к неинвариантности относительно преобразования Галилея уравнение полной энергии смеси.

Для понимания причины неинвариантности относительно преобразования Галилея уравнения полной энергии смеси разобьем уравнение (7) на элементы. С этой целью получим уравнения сохранения кинетической энергии газа и частиц соответственно в случае T₂ <  T S и проверим их на инвариантность относительно преобразования Галилея.

Умножая уравнение сохранения импульса газовой фазы (4) на v1 , а уравнение сохранения импульса конденсированной фазы (5) на v2 , получим уравнения сохранения кинетической энер- гии газа и частиц соответственно v1

^д Р 1 ^V 1 . ^д Р 1 ^v 1² . „ ^д p  _ _{fv v}  ^др 2 ^v 2 . ^д Р 2 ^v 22 . ³ „ ^д p

= fV ₂ ,

++ а      = - / V i, V n++ а^

д t      дx      1 дx           1   д t       дx     2 2 дx которые после простых преобразований принимают следующий вид v2

^{д р} 1Т д t

v 1 ²

^{P 1 1} 2         д p

+---. — + а1 V13" = -fv1, дx         дx

v ²

^дР2:Г д t

+

v 2 ²

^P v ²₂   3     д p „

---5----⁺ 3 ^а 2 ^V 23- = ^fv 2 , д x     2     д x

Проведем анализ инвариантности относительно преобразования Галилея уравнений сохранения кинетической энергии газа и частиц (26) и (27) соответственно. С этой целью переходим в

Математика

новую систему координат в соответствии с соотношениями (14)–(18). В новой системе координат уравнение сохранения кинетической энергии газа имеет следующий вид

1 дР1 (V1н - D f  1  Эр (V н - D)2  1 Эр (viн - D)(V н - D^d

1 D 1+ a V i — D — —

2 dt 2         dx          2            dx                 1V 1 н     *Xx'

ннн

После проведения необходимых преобразований получим v2 v2

^d p 1 ' н     ^дР 1 ^V 1 н

---2- +----- ²--D d t          d x„

н

" ^д Р 1 ^V 1 н + ^д Р 1 ^V 1 н ^V 1 н

( d t

дx_K н

+ ¹ D

, 2 f ^дР 1 + ^d P 1 ^V 1 н d t     д x_H

н

d p       d p „

^{+ a} 1 ^V 1 н 3 ^a 1 D^— ^{— —} f^V 1 н ⁺ fD .

dxH      dxH нн

Здесь четвертый член в левой части уравнения равен нулю в соответствии с уравнением (1), а третий в соответствии с уравнением (4) равен a1 D -p- + fD.

^{d Х} н

Таким образом, в новой системе координат уравнение сохранения кинетической энергии газа записывается в виде v2

^д Р 1 1^ ^дP ^{V V} 1 н

д t

дx_K н

дРс

^{+ a} 1 ^V 1 н ^ ^{— — fV} 1 н • ^{д Х} н

Уравнение (28) полностью совпадает с уравнением (26), следовательно, уравнение сохранения кинетической энергии газа (26) инвариантно относительно преобразования Галилея. Аналогично показывается инвариантность относительно преобразования Галилея уравнения сохранения кинетической энергии частиц (27).

Таким образом, из четырех составляющих, входящих в уравнение сохранения полной энергии смеси (7), три являются инвариантными относительно преобразования Галилея: уравнение сохранения внутренней энергии частиц (6), уравнение сохранения кинетической энергии газа (26) и уравнение сохранения кинетической энергии частиц (27). Следовательно, неинвариантным относительно преобразования Галилея является уравнение сохранения внутренней энергии газа. А это значит, что математическая модель, представленная уравнениями (1)–(13), не может пра- вильно описывать условия зажигания твердого топлива.

Заключение

По результатам проведенного в работе анализа инвариантности относительно преобразования Галилея законов сохранения математической модели перехода конвективного горения твердого унитарного топлива во взрыв можно сделать следующие выводы:

• 1.    Уравнения сохранения массы (1), (2), импульса (4), (5), внутренней энергии конденсированной фазы (6), кинетической энергии фаз (26) и (27) являются инвариантными относительно преобразования Галилея;

• 2.    Уравнения сохранения внутренней энергии газовой фазы и уравнение сохранение полной энергии смеси (7) не являются инвариантными относительно преобразования Галилея;

• 3.    Данная математическая модель не может правильно прогнозировать переход конвективного горения твердого унитарного топлива во взрыв.

Автор выражает свою благодарность профессору В.Ф. Куропатенко за полезные обсуждения и интерес к работе.