Анализ изменений геометрии и кинематики зубчатой передачи в условиях абразивного изнашивания

Исследования надежности современных сельскохозяйственных, пищевых и горных машин и механизмов показывают, что до 40% отказов приходится на долю агрегатов трансмиссии, работоспособность которых в значительной мере регламентируют зубчатые колеса. Так при капитальном ремонте из-за износа и усталостного разрушения выбраковывается свыше 60% зубчатых колес [1–5]. Основная доля отказов агрегатов трансмиссий приходится на коробку передач – до 45%. Деталями, лимитирующими долговечность коробки передач, являются зубчатые колеса, которые у тракторов сельскохозяйственного назначения подвержены в большей степени абразивному изнашиванию, так как их эксплуатация происходит в условиях высокой запылённости воздуха и недостаточной герметичности внутренних полостей смазочной системы трансмиссии.

В результате износа зубьев колес появляются вибрации, возрастают динамические нагрузки в приводах. Все это в большей степени связано с изменением кинематики зубчатого зацепления при износе.

Определение геометрических, кинематических и качественных показателей зубчатых зацеплений преимущественно проводится с использованием аналитически методов. Это связано с тем, что, как отмечается в ряде исследований, геометрические построения, используемые для анализа изменения параметров зацепления, не дают необходимой точности и полной картины формирования возбуждающих колебательных процессов, вызванных изменением функции передаточного отношения. Характер последних предопределяет кинематический анализ зацепления пары зубчатых колес на всех стадиях их износа под нагрузкой. Что позволяет не только определить угловые скорости и ускорения колес, но и определить линейные скорости и ускорения в относительном движении пары зубьев, что предопределяет условия изнашивания на всем участке зацепления пары зубьев и позволяет прогнозировать физику процесса и, соответственно, скорость изнашивания по высоте зуба.

Основной целью анализа зубчатого зацепления состоит в выявлении закона изменения передаточного отношения, особенно при наличии изношенных профилей сопряжённых зубьев [7–11]. Методы исследования, используемые в теории зубчатых зацеплений, условно можно разделить на методы дифференциальной геометрии, кинематические, синтетические. Проведенные нами исследования кинематических и геометрических характеристик зацепления опираются, главным образом, на кинематические методы, которые позволили в ряде случаев упростить математические выкладки по сравнению с другими методами. В общем случае‚ анализ сводится к отысканию уравнения зацепления изношенного профиля, при известной зависимости изменения функции передаточного отношения при износе силовой зубчатой передачи. Решение этой задачи важно для оценки рабочих характеристик зубчатых передач приводов машин и прогнозирования их срока службы.

Цель работы – исследование изменений геометрии и кинематики зубчатых передач в условиях абразивного изнашивания.

Материалы и методы

Анализ литературных источников российских и зарубежных авторов [12–16] показывают, что изменения профилей зубьев при износе более 3–5% силовых передач разного модуля, разного передаточного отношения, разной твердости и коэффициентов смещения исходного контура, различных трансмиссий в сельскохозяйственных, транспортных машинах (тракторы, комбайны), имеет несомненную схожесть. Причем было отмечено определённое различие изношенных профилей ведущего и ведомого колес. Исходя из этого, а также статистического анализа, были смоделированы профили изношенных зубьев шестерни и колеса. В каждом конкретном случае профиль зуба описывался полиномом в системе координат, жестко связанной с шестерней (колесом). Для анализа изношенного зацепления вводится три системы координат: подвижные системы S1 и S2, которые связаны с шестернёй и колесом, а также неподвижная система S, жестко закреплённая относительно стойки. Геометрия зубьев исследуемых шестерён описывается системой уравнений в системе координат S1 (х1; y1; z1):

x i = E ^Ck ( y, ^- r f 1 ) ^k;

k = 0

0,25 m <  ( y_x - r^ ) <  2.25 m ;

x 2 = E D k ( y 2^- r f ₂ ) k ;

k = 0

0,25 m <  ( y ₂ - r ^) <  2.25 m ,

где rl, r2 - радиус окружности впадин шестерни и колеса, мм; т - модуль зацепления, мм; Dk, Ск - коэффициент полинома; к - степень полинома.

Анализ проводится в десяти сечениях по высоте зуба и на разных стадиях износа. Кроме того, для уточнения результатов рассматриваются дополнительные факторы: влияние эксплуатационных нагрузок, изменения формы зубьев в процессе работы и их воздействие на точность передачи движения. Эти исследования позволяют более детально оценить распределение контактных напряжений и нагрузок, что является ключевым моментом при разработке износостойких и надёжных зубчатых передач.

Результаты и обсуждение

Профили зубьев шестерни и колеса, а также орты нормали в неподвижной системе координат S (x; y; z) описываются с помощью уравнений.

• x () = x cos ^ - y sin ^ ;

y () = X 1 cos ^ - У 1 Sin ^ ;

x( ' = x ₂ cos ^ ₂ + y sin ^ ₂;

y ' = - x ₂ cos ^ + y ₂ cos ^ ₂ + а_ш ;

y ⁽ ) = - x ₂ cos p₂ + y ₂ cos ^ ₂ + а_ш , где (p i и ( 2 - углы поворота колёс относительно стойки; И - орты нормалей в соответствующей системе.

В точке касания профилей у них должны быть равны радиусы векторы и орты нормали, основываясь на этом, получим следующее уравнение:

• x cos ^ - y_t sin ^ = x ₂ cos ^ + y_t sin p₂ ;

x sin ^ + y cos ^ = - x ₂ cos ^ ₂ +

+ y 2 cos ^ 2 + а _ш ;

l x ^cos ^ 1 ^{- l}y ^sin ^ 1 = l x ^cos ^ 2 ⁺ l y ₂ ^sin ^ 2 ;

7k x=TCk (y1- rf) ;                    (3)

k = 0

0,25 m < ( y^ - r_f[ ) < 2.25 m ;

• ^x 2 = E D k ( y 2 ^- r f 2 ) k ;

k = 0

0,25 m < ( y ₂ - y₂ ) < 2.25 m .

В данном случае существует пять уровней, которые связывают шесть параметров: p i , x i , y i , ( 2 , X 2 , y 2 . При заданном угле поворота pi в интервале от -0,5я до 0,5я с шагом 1 ° мы можем, используя систему уравнений (3), вычислить остальные параметры в зависимости от ^

Для нахождения функции передаточного отношения была продифференцирована зависимость ф₂ = ф₂ ( ^ ) . При этом учитывалось, что i ₂₁ = d ^ /dq\ = ^ ( ^ ) .

В процессе решения системы уравнений 3 мы также получаем координаты точки контакта для каждого значения угла p i . Эти точки контактных взаимодействий на изношенных профилях зубьев, как известно, определяют линию зацепления, которая является важнейшей характеристикой работы зубчатой передачи. Такая линия зацепления непосредственно влияет на качество и эффективность передачи движения в системе.

Кроме того, нами был выполнен аналитический синтез изношенной передачи с использованием тех же координатных систем, которые применялись при анализе. В ходе экспериментальных исследований был получен закон изменения передаточного отношения, представленный в виде рядов Фурье, а также профиль зуба, который был выражен через степенной ряд. Эти данные позволили провести синтез зацепления и вычислить профиль зуба колеса, после чего его форма была сопоставлена с результатами, полученными в ходе испытаний, что позволило оценить точность и корректность полученных теоретических моделей.

Исследование геометрических и кинематических характеристик зацепления основывается на кинематических методах, которые особенно эффективны при анализе вариаций в отношениях скоростей, когда ii2 ^ const. Эти методы позволили значительно упростить сложные математические выкладки и расчёты, что стало возможным благодаря их высокой точности и удобству применения в условиях изменяющихся параметров.

Анализ функции передаточного отношения, полученной нами в экспериментах на передачах разного модуля (2; 3; 4; 5 мм), разной твердости (HRC45, HB 350) со смещением исходного контура и без смещения (рисунок 1), показал, что экстремальные значения функции передаточного отношения, если использовать основную теорему зацепления [1, 2].

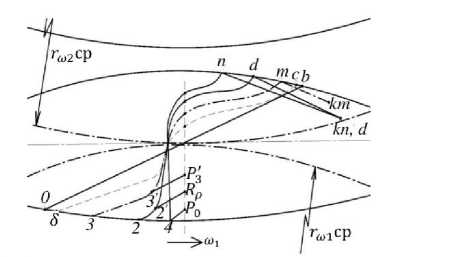
Рисунок 1. Изменение линии зацепления при изнашивании (∆S=0%; 3%; 5%; 8%; 25%; m=5 мм; z 1 /z 2 = 18/30) Figure 1. Changing the engagement line during wear (∆S=0%; 3%; 5%; 8%; 25%; m=5 mm;) z 1 /z 2 = 18/30

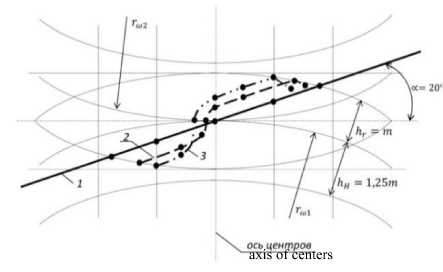
Рисунок 2. Линии зацепления при износе, построенные по результатам аналитического расчета (1-∆S=0%; 2-∆S=5%; 3-∆S=25%)

Figure 2. Lines of engagement during wear, constructed according to the results of an analytical calculation (1-∆S=0%; 2-∆S=5%; 3-∆S=25%)

Анализ графиков, полученных в результате проведённых опытов и выражающих функцию передаточного отношения, показывает, что её значение может быть представлено корреляционной зависимостью:

Экстремальные значения функции передаточного отношения определяются с использованием основной теоремы зацепления (рисунок 1):

Учитывая, что крайнее положение полюса зависит не только от модуля, но и от величины износа, в зависимости вводится коэффициент к д^ отражающий степень изношенности передачи.

Поскольку коэффициент к д 5 влияет не на r ω1 и r ω2 , а на расстояние крайних положений мгновенного полюса от R 0 , зависимости (3) для различных степеней износа могут быть записаны следующим образом:

max i 12	r max	z2 + 1.8 k^s
	= m in rω 1	Z 1   1.8 k Л S
max i 12	min =-r^	— z 2 — 1.3 k Л S ,	(4)
	max rω 1	Z 1 + 1.3 k л s

_ 1,1 ^Л S -1,1 ^{- л} S

А S = 1,1Л S + 1,1-л S , где ЛS - относительная величина износа,%; rmin , rmax , rmax , rmin – минимальные и макси-ω1        ω1       ω2      ω2

мальные значения мгновенных радиусов центров вращение шестерни и колеса.

Применяя кинематический метод, мы находим уравнение зацепления п_{ у. ’ = 0, как произведение векторов нормали и скорости относительного движения, в соответствующей – i -й системе координат.

Представим уравнение зацепления, как скалярное произведение векторов для профилей зуба шестерни, и объединив его с системой уравнений (4), получим следующее выражение:

x i = £ c K ( y i^- rf .) k ¹;

K=1 max    min n in =—+ 12  9 12 £Aj sin (j^yi + ^j) ;

z ^{1        2}      j"                       (5)

z 2 ^{+ 1.8 k} Л S .  min _ z 2   ^{1.3 k} Л S .

z 2 -1.8 k Л S ’  ¹²   “z 2 + 1.3 k Л S ;

1.1 ^Л S -1.1^{- Л} S

1.1 ^Л S + 1.1^{- Л} S ‘

max i 12

k А S

Для решения этого уравнения необходимо, установив значение износа и задав угол поворота шестерни ^ в пределах интервала, —0,5 ^ <  ^ <  0,5 ^ вычислить координаты контактной точки в соответствующей системе координат. На основе полученных данных, уравнение линии зацепления, которое представляет собой множество точек контакта, определяется в неподвижной системе координат S. Эти вычисления позволяют более точно моделировать поведение зацепления и его изменения в зависимости от износа и угловых перемещений

Теперь, используя матрицы перехода от одной системы координат к другой, опираясь на ранее полученные выражения, можно вычислить координаты любой точки, лежащей на линии зацепления, что позволяет точно определить геометрию взаимодействующих профилей. Профиль зуба колеса, в свою очередь, можно рассматривать как огибающую однотипного семейства профилей зуба шестерни, которые движутся относительно друг друга. Исходя из этого, уравнение профиля зуба колеса, представляющего собой совокупность характеристик в системе координат S2, может быть записано в следующем виде, что дает возможность детально проанализировать форму и особенности работы зацепления в разных точках.

Таким образом, с использованием вышеупомянутых выражений, мы можем получить искомый профиль зуба колеса. При сравнении этого профиля с экспериментально полученным результатом видно, что отклонение не превышает 4%, что служит убедительным подтверждением точности предложенных зависимостей и их возможности для применения в инженерных расчетах.

Существенное влияние на износ зубьев оказывают особенности геометрии и кинематики зубчатого зацепления [4, 17–19]. За время прохождения площадки контакта над данной точкой поверхности при взаимодействии пары зубьев изменяются удельная скорость скольжения, приведенный радиус кривизны р . Эти методы позволяют получить более точные данные, которые необходимы для дальнейшего анализа. Более точное определение данных параметров аналитическими методами позволит повысить качество расчетов на износ, разработать рекомендации по оптимизации конструкции пар трения и технологий поверхностного упрочнения, усовершенствовать методики испытаний на износостойкость. Для этого необходим учет влияния на процесс изнашивания кинематики относительных перемещений и динамики нагружения звеньев машин, обусловленных функционированием пары трения в машинном агрегате.

Исходя из теории трения и изнашивания твердых тел в различных условиях с учетом физики явлений, протекающих в зонах контакта взаимодействующих поверхностей предложенной И.В. Крагельским [6], в зацепления влияние кинематических и геометрических факторов на процесс износа зубьев традиционно выражается через коэффициенты удельного скольжения т или скорости от относительного скольжения V ^{( 12 )} , которые позволяют более точно оценить степень воздействия этих факторов на износ и долговечность зубчатых передач, а геометрические через кривизну контактирующих профилей K [4].

Компоненты V ^{( 12 )} , V ¹ и V- ²⁾ , которые присутствуют в приведенной формуле, взяты по модулю. Однако важно отметить, что знаки этих компонентов, отражающие их направления относительно друг друга, также учитываются в расчетах. Это необходимо для более точного моделирования взаимодействия элементов системы. Векторы скоростей перемещения контактной точки в процессе относительного движения по профилям зубьев, с учётом их направления и величины, можно выразить следующим уравнением, что позволит детально анализировать динамику зацепления и взаимодействие шестерни и колеса.

Для нахождения частной производной, которая находится в правой части уравнения, необходимо продифференцировать выражения (2) и (3). Это позволит получить необходимую зависимость, учитывая влияние каждого из параметров на конечный результат.

v ⁽²)   ,      ,    v(°

=Т« ^-п 1 ^-;

VKVK

V„_ ^дr, ⁽ xi,У^^дf ⁽ x i ,У  dy i.

V K = dt

сЩ

d r -C x p y).

^d У 1

^d r 2 ( x 2 , У 2 ) ^d У 2

1 £ KC k ( У 1 - Г 1

k –1

)    + j ;   (6)

K = 1

= 2₂ £ ^kd k ( У 2 ^- r f 2 ) k ¹ + j 2 ;

K = 1

у ( ¹² ) _ у( ² ) _ у ¹

V        VK VK , где V – скорость относительного движения

(скорость скольжения) колес; V(1) и V2) — ско- рость перемещения точки контакта по поверхностям зубьев шестерни и колеса, соответственно; i=1,2 – индекс, указывающий шестерню и колесо

Для определения вектора скорости относительного движения необходимо учесть изменения координат во времени, что можно выразить через производные координат.

Таким образом, коэффициент удельного скольжения определяется с учетом систем уравнений (1), (2) и (5), что позволяет точно учесть все необходимые параметры и их взаимное влияние. Полученная зависимость предоставляет более полное понимание процессов, происходящих в системе, и помогает точно вычислить этот коэффициент для различных условий эксплуатации.

Кривизны поверхностей в нормальном сечении являются одним из основных геометрических параметров зацепления, определяющих несущую способность передачи. Они позволяют выразить радиус кривизны сопряжённых профилей. Как упоминалось ранее, приведённые радиусы кривизны, вместе с удельными скольжениями, входят в применяемую методику расчёта скорости изнашивания.

Для вычисления кривизны зуба шестерни и колеса K , K применяется метод дифференциальной геометрии:

1.5

• ^{1    +} ( x 1 )

K 2 (VW + V(12 ’) = K1Vw - (w(1) - w(2 ’) e(1); (7) x1=£n (n-1) AX-2;

n = 0

n = 7

x 1 =£ ^пАп У' ^{п -1} , n = 0

где K, K – кривизна зубьев шестерни и колеса соответственно; e – вектор орта нормали в си- (1) Ч 2)

стеме координат; w и w – векторы угловых скоростей шестерни и колеса соответственно.

Для нахождения решения по формуле (7) запишем уравнение нормали в виде 1

e ⁽⁾ = i sin у - j cos у , после чего, применяя коллинеарность (отношение параллельности) векторов ( w ^¹^ - w ⁽²) ) e ^, а также преобразуя зависимость нормали в скалярную форму, получим зависимость для определения приведенной кривизны профилей по линии их зацепления – K .

V ( ² ) = V W+ V < ¹² ) ;

V ( ² ) = V к + KV к¹) = V 'к ¹ ) ( 1 + K ) ; KK KK

44 444^42

к =

dya

dt

Ч[ к 2 ( 1 + к ) - к 1 ] = -

w^ e ^

В данном случае учитывается, что векторы V ¹ ) и e = ( e_y i + e_xJ ) коллинеарные. Учитывая, кривизна и радиус кривизны обратные функции получим р =1\ к .

Для расчета величин износа сопряженных поверхностей необходимо учитывать их относительное скольжение, зависящее от радиусов кривизны и кинематики относительных перемещений в паре трения и связанное с относительной скоростью. Ниже приводятся графики изменения этих параметров определенных нами аналитически для шестерни и колеса при износе 18% в сравнении с приведенными зависимостями для аналогичной не изношенной передачи для шестерни и колеса, соответственно. Видно, как значительно изменяется произведение приведенного радиуса кривизны р = ^1^2 и коэффициента пр' P1 + Р2

удельного скольжения р\_рц , которое лежит в основе расчетов скорости изнашивания [13] и как резко изменяется приведенный радиус кривизны, который влияет на величину контактных напряжений.

■ 2

JL + +— i i2__ l    w (i) .

^{1 + K} ^2 ( 1 + к ) V K ¹

actual engagement axis

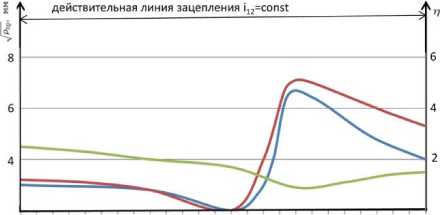
0123456789 10 11 12 13 14 15 16 17 18 19 20 21 22 Vi. град

(a)

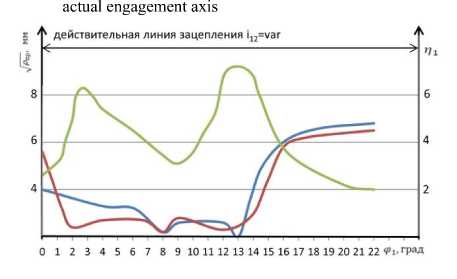
(b)

Рисунок 3. Диаграммы распределения п , рр , ( , рР ) по углу поворота шестерни из выражений (6) и (7)

(z i =17, m=5 мм, AS=8%): a - i_n = const ; б - i_n = var

Figure 3. Distribution diagrams n , pp , ( , pp ) according to the gear rotation angle from expressions (6) and (7)

(z 1 =17, m=5 mm, ΔS=8%)

Заключение

• 1.    В процессе абразивного изнашивания тяжело нагруженных передач происходит не только изменение формы профилей зубьев, но и изменение закона относительного движения колёс. Функция передаточного отношения И2 перестаёт быть постоянной и приобретает гармонический характер, причём период её

• 2.    В процессе изнашивания линия зацепления искривляется, а её начало, и конец сдвигаются в направлении вращения зубчатых колёс. Коэффициент перекрытия при этом постепенно снижается, но при степени износа свыше 18–20% стабилизируется в пределах 1,03–1,1.

• 3.    С изменением линии зацепления меняются условия изнашивания, связанных с удельным скольжением и приведенным радиусом кривизны.

• 4.    Изменения линии зацепления в процессе изнашивания проявляют схожую тенденцию при различных модулях, передаточных числах, твёрдости зубьев, а также при наличии или отсутствии смещения исходного контура.

• 5.    Разработаны аналитические зависимости, которые позволяют выполнять расчёты геометрических, кинематических и качественных характеристик передачи и прогнозировать скорость изнашивания шестерни и колеса, оценивать величину контактных напряжений и коэффициента удельного скольжения по линии зацепления пары зубьев на различной стадии износа.

колебаний совпадает с периодом зубцовой частоты. На начальных стадиях износа размах колебаний И2 быстро увеличивается. Однако с ростом степени износа темпы увеличения размаха снижаются, и при износе, превышающем 15–20%, размах практически стабилизируется. Также наблюдается, что увеличение модуля передачи приводит к росту размаха колебаний.

Значения колебаний i12 при изнашивании могут быть достаточно большими. В ходе экспериментов установлено, что при износе порядка 18% и более, а также при малом числе зубьев шестерни, отношение И2тах к H2min достигало 1,3.