Анализ эффективности алгоритмов вычисления в информационной системе логико-математического моделирования

Логико-математическое моделирование динамических систем является важным направлением математического и компьютерного моделирования. Совершенствование методов логико-математического моделирова-ния динамических систем повышает эффективность автоматизации решения задач математического моделирования.

Актуальность данной работы в настоящее время вызвана повышением роли логико-математического моделирования, которая заключается в возможности трансформации полученной логико-математической модели в предметно-математическую модель в виде программы для ЭВМ, осуществляющей компьютерное моделирование исследуемых систем.

В работе [1] был предложен метод представления знаний в виде функциональных грамматик и построения математических моделей в виде суперпозиции функций с помощью полного вывода в соответствии с заданными правилами. В основе таких логико-математических моделей лежит продукционная система, описанная неполной функциональной контекстно-свободной грамматикой. Это позволяет расширить возможности продукционных систем знаний и создавать программные комплексы математического моделирования динамических систем с возможностью использования в разных предметных областях.

Представленная таким образом методика моделирования динамических систем, на основе аппарата функциональных грамматик, позволяет встраивать в модели численные методы расчета характеристик систем. Основу методики составляют алгоритмы построения дерева, порождения и интерпретации вычислительных алгоритмов в виде суперпозиции функций из заданного базового набора. Важным достоинством такого подхода служит, в частности, возможность не только строго и последовательно описать качественные взаимосвязи предметной области, но и генерировать в символьном виде точные количественные зависимости, существующие в ней.

Система способна решать задачи анализа и синтеза, эффективно используя известные численные методы. Важно отметить, что такая автоматизированная система способна решать как прямые, так и обратные задачи математического моделирования из разных предметных областей. В то время как большинство коммерческих продуктов способно решать только часть прямой задачи моделирования,

Работоспособность метода и алгоритмов программного комплекса [1; 2] была продемонстрирована при решении задач на примере баз знаний из областей механики и радиотехники. При этом был сформирован набор необходимых понятий, разработан алфавит символов грамматики, даны отношения между понятиями, создана соответствующая система правил и определены функциональные зависимости, входящие в состав правил вывода.

Для реализации системы логико-математического моделирования динамических систем, представленной в оригинальной работе [2, с. 38], автором были приведены аргументы в пользу выбора функциональной парадигмы программирования. А для реализации метода в виде алгоритма рекомендуется использовать язык программирования Lisp. В связи с этим возник вопрос об универсальности метода и возможности его реализации на других языках. Кроме того, не хватает сравнительного анализа эффективности при реализации метода между выбранным языком и другими популярными языками программирования.

Цель исследования

Цель исследования – провести системный анализ автоматизированной системы логико-математического моделирования динамических систем, использующей аппарат функциональных грамматик. В частности, необходимо проанализировать процессы обработки информации, происходящие внутри системы.

Для достижения цели необходимо решить следующие задачи:

• •    Анализ структуры, параметров и основных методов обработки информации автоматизированной системы;

• •    Анализ реализации оригинального метода в виде алгоритма на языке функционального программирования Lisp;

• •    Разработка модифицированного алгоритма на языке императивного программирования Python;

• •    Сравнительный анализ эффективности реализаций метода на языках программирования Lisp и Python.

Материал и методы исследования

В процессе исследования были использованы методы системного анализа, такие как анализ, синтез, обобщение, сравнение, декомпозиция, конкретизация, формализация, моделирование, алгоритмизация, тестирование, оценивание.

Кроме того, были использованы инструментальные средства разработки алгоритмов: язык программирования Python (интерпретатор CPython) и язык программирования Lisp (интерпретатор CLISP).

Теоретическая часть

Рассматриваемая автоматизированная система логикоматематического моделирования динамических систем реализована в виде алгоритмов на языке функционального программирования Lisp [3]. Структуру системы можно представить в виде двух модулей: модуля базы знаний и модуля вывода решения.

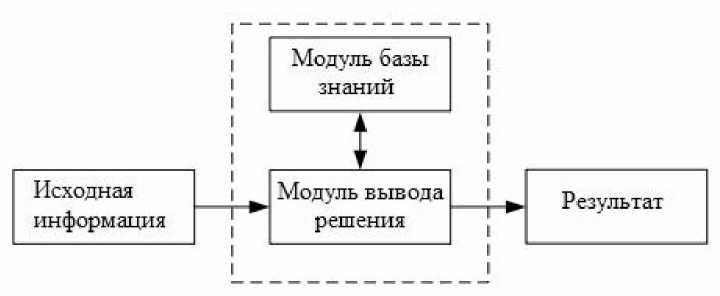
Рис. 1. Структура системы

Модуль базы знаний хранит введенную информацию о понятиях предметной области в символьном виде, практически так же, как в базах данных. Отличие заключается лишь в структуре базы. В терминах языка Lisp база знаний представляется в виде глобальной переменной — динамического списка (многомерного массива), состоящего из подсписков, содержащих в себе элементы (символьные переменные), обозначающие понятия из выбранной предметной области. Количество подсписков и содержащихся в них элементов вместе с их названиями определяется в соответствии с правилами вывода, заданными некоторой неполной контекстносвободной функциональной (формальной) грамматикой.

Модуль вывода решения состоит из множества функций, выполняющих обработку информации, хранящейся в базе знаний. Для запуска механизма вывода решения определенной задачи необходимо выполнить функцию с именем «Решение», которая имеет вид:

(Решение '() Механика)

Функция состоит из двух аргументов. Первый аргумент представляет собой список из символов (переменных параметров), а второй задает название базы знаний, в рамках которой необходимо произвести поиск решения. При этом важно, чтобы в списке символов в качестве первого элемента был указан начальный нетерминальный символ, обозначающий то, что нужно найти, а последующие за ним терминальные символы должны обозначать то, что дано.

Ключевым алгоритмом всей системы как раз и является поиск правильной цепочки — суперпозиции функций из множества заданных правил вывода . При этом в правилах вывода совершенно не используются такие логические операции, как and, or, not и другие. Метод поиска решения основан на обходе дерева и многократной замене одних элементов из подсписков другими.

Вначале механизм вывода строит дерево перебора на основе базы знаний. А далее, начиная с заданного начального нетерминального символа (узла), в процессе обхода всего дерева происходит формирование итоговой суперпозиции функций, представляющей собой символьный результат решения задачи:

(f12 (f17 (f18 ) ) )

Если вместо исходных аргументов , , , подставить численные значения задачи, то за счет выполнения функций f18, f17, f12, описанных в базе знаний, будет получено общее решение. В системе для этого необходимо выполнить функцию с именем «Решение1»:

(Решение1 '( ( 0.3) ( 20) ( 4) ( 0.05)) Механика)

Таким образом, результатом работы механизма вывода автоматизированной системы логико-математического моделирования является суперпозиция функций, которая представляет универсальный результат, т.к. вместо ее формальных параметров будут поданы фактические параметры и получен конкретный численный результат решения задачи моделирования.

Работоспособность рассмотренных выше оригинальных алгоритмов была продемонстрирована при решении задач на примере баз знаний из областей механики и радиотехники. Выполнение алгоритмов производилось в интерпретаторе HomeLisp [4]. Однако данный интерпретатор не обладает высокой производительностью и предлагается к использованию только для целей обучения. Кроме того, при реализации интерпретатора HomeLisp его автор счел целесообразным не использовать отдельные библиотеки, а включать все функциональные возможности прямо в ядро по мере развития проекта. Это накладывает большие ограничения в плане анализа эффективности алгоритмов. Из-за недостатка встроенных функций анализа времени выполнения алгоритмов было решено использовать более производительный интерпретатор CLISP [5]. Так как авторы CLISP следуют стандарту диалекта Common Lisp [6], а интерпретатор HomeLisp является собственной реализаций, то часть алгоритмов и функций пришлось переписать из-за имеющихся синтаксических различий в коде, приводящих к ошибкам выполнения.

Для исследования анализа эффективности оригинального алгоритма был предложен собственный модифицированный метод поиска суперпозиции функций, а также его реализация на языке программирования Python. Формально описание данного метода можно представить следующим образом.

Пусть имеется база знаний, описанная следующей грамматикой: G = (Vt, Vn, P, S), где множество правил вывода Р =

{ Spd2 → Spd 1,	Accl ,	Time ;	Spd2	→ Accl ,	Dist ,	Spd 1;
Spd2 → KinEn 2, Mass		;	Spd1	→ Spd 2,	Accl ,	Time ;
Spd1 → Dist 1,	Time ,	Accl ;	Spd1	→ Spd 2,	Accl ,	Dist ;
Spd1 → KinEn 1	, Mass	;	Dist	→ Spd 1,	Time ,	Accl , Time
Dist → Spd 2,	Spd 1,	Accl ;	Dist → OpPull ,		FrPull ;
Dist → OpFric ,	FrFric	;	Time → Spd 2,		Spd 1,	Accl ;
Time → Spd 1,	Accl ,	Dist ;	Accl	→ Spd 2,	Spd 1,	Time ;
Accl → Dist ,	Spd 1, Time ;		Accl	→ Spd 2,	Spd 1,	Dist ;

Accl → FrPull ,	rFric , Mass ;	Mass → FrPull ,	FrFric ,	Accl ;
Mass → FrFric ,	CfFric , Accl ;	Mass → KinEn 2,	Spd 2;
Mass → KinEn 1,	Spd 1;	FrPull → FrFric ,	Mass ,	Accl ;
FrPull → OpPill ,	Dist ;	FrFric → FrPull	, Mass ,	Accl
FrFric → Cfg , CfFric , Mass ;		FrFric → OpFric	, Dist ;
CfFric → FrFric ,	Mass , Cfg ;	KinEn2 → Mass ,	Spd 2;
KinEn2 → OpPull ,	OpFric , KinEn 1;	KinEn1 → Mass ,	Spd 1;
KinEn1 → KinEn 2,	OpPull , OpFric ;	OpPull → FrPull ,	Dist ;
OpPull → KinEn 2,	KinEn 1 OpFric ;	OpFric → FrFric ,	Dist ;

OpFric → OpPull , KinEn 2, KinEn 1;}

Vt — множество терминальных символов, обозначающих изначально известные величины, используемые в процессе поиска решения какой-либо задачи. Vn — множество нетерминальных символов, обозначающих неизвестные величины в решаемой задаче. S — нетерминальный символ из множества Vn, означающий то, что нужно найти в процессе решения. Множество правил вывода Р фактически включает в себя полный алфавит всех используемых символов. Определения символов представлены в работе [2, c. 45].

Так как правила грамматики имеют строго заданную (направленную) последовательность вывода, то множество Р можно преобразовать в направленный (ориентированный) мультиграф, представив его в виде списка смежности. В таком случае, например, правило «Spd2 → Spd1, Accl, Time;» будет означать то, что с вершиной Spd2 связаны (из нее выходят) вершины Spd1, Accl и Time. Используя данный принцип, после преобразования всех правил получим мультиграф G = (V, E), который имеет следующий вид:

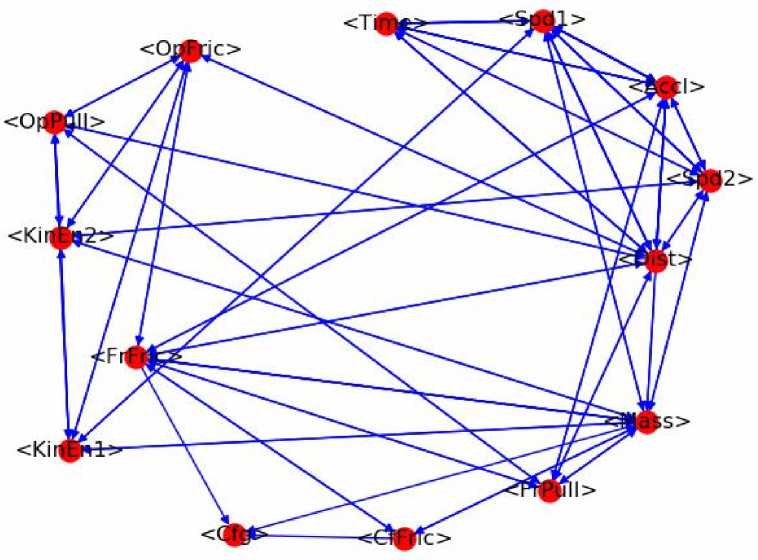
Рис. 2. Ориентированный циклический мультиграф

В получившимся мультигафе, описывающем понятия какой-либо предметной области, можно будет выполнять поиск решения задач. Формально решение задачи будет представлять собой поиск в мультиграфе G = (V, E) остовного дерева (ациклического связного подграфа), включающего в себя указанное подмножество известных (терминальных) вершин, а также некоторых неизвестных (нетерминальных) вершин, соединяющих между собой известные. Если такой подграф будет найден, то это будет означать, что задача имеет решение. В противном случае задача будет считаться как не имеющая решения. Таким образом, найденное правильное решение какой-либо задачи будет представлять собой строго последовательную цепочку, состоящую из объединенных между собой нетерминальных вершин, которая обязательно должна начинаться с вершины, обозначенной в задаче как то, что требуется найти. Более подробное описание и реализация алгоритма предложенного метода будут приведены в отдельных публикациях.

Практическая часть

Анализ эффективности алгоритмов системы проводится с применением собственной методики, использующей в основе метод имитационного моделирования. В качестве показателей эффективности выбираются два наиболее важных параметра: общее время выполнения алгоритма и общее количество используемой алгоритмом памяти. В процессе моделирования многократно воспроизводятся функции работы системы и измеряются общие показатели эффективности. На основе результатов может проводиться дальнейшая оптимизация (модификация) структуры системы. Затем имитация повторятся заново. В итоге та реализация алгоритма, показатели которой принимают наименьшие значения, признается более эффективной.

Для анализа производительности алгоритмов в интерпретаторе CLISP имеется встроенная функция time. Данная функция может принимать в качестве аргумента другую функцию или фрагмент кода, а по окончании его выполнения отображать информацию о затраченном времени и количестве используемой памяти.

На рисунке 3 показаны результаты работы функции time, отображающие информацию о работе алгоритма поиска и вывода суперпозиции функций с количеством повторений 1300 раз.

(F12 (F17 (F18 ) ) ) Real time: 1.249933 sec.

Run time: 1.241812 sec.

Space: 16027792 Bytes

GC: 19, GC time: 0.044993 sec.

Рис. 3. Результаты анализа производительности алгоритма в интерпретаторе CLISP

Из рисунка видно, что время работы оригинального алгоритма составило 1,249 с. А количество используемой памяти равно 16027792 байтам. Имея результаты эффективности работы оригинального алгоритма, реализованного на языке Lisp, можно перейти к анализу собственной модифицированной реализации на языке императивного программирования Python [7].

В модифицированной реализации метода на языке Python база знаний выстраивается с использованием структуры данных — упорядоченного словаря. За счет этого достигается экономия времени доступа к данным. Сам алгоритм поиска и вывода суперпозиций построен на основе трех небольших функций, которые осуществляют ввод исходных данных, поиск и построение суперпозиции, подстановку численных значений и вычисление результата. Кроме того, алгоритм не строит дополнительного дерева перебора на основе базы знаний, что позволяет значительно сэкономить количество используемой памяти и избежать комбинаторного взрыва. Для запуска и проверки работы алгоритма используется стандартный интерпретатор языка — CPython. Он также содержит встроенные модули и функции для анализа производительности алгоритмов. Для измерения затраченного времени и памяти были использованы функции из модулей timeit и tracemalloc.

На рисунке 4 показаны результаты анализа производительности алгоритма поиска и вывода суперпозиции функций на языке Python с количеством повторений 1300 раз.

fl2(fl7(fl8(,),,),)

Время выполнения:: 0.3246627059997991 сек.

Памяти использовано:: Текут. - 240076 байт, Макс. - 284236 байт

Рис. 4. Результаты анализа производительности алгоритма в интерпретаторе CPython

Результаты показывают, что общее время выполнения алгоритма составило 0,324 с. А максимальное количество используемой памяти равно 284236 байтов.

Результаты исследования

По итогам проведенного исследования были получены следующие результаты:

• •    Выполнен анализ структуры, параметров и основных методов обработки информации в автоматизированной системе логикоматематического моделирования;

• •    Рассмотрена оригинальная реализация метода в виде алгоритма на языке функционального программирования Lisp;

• •    Разработана модифицированная реализация метода в виде алгоритма на языке императивного программирования Python;

• •    Проведен сравнительный анализ эффективности реализаций метода между языками программирования Lisp и Python. В таблице 1 приведены основные результаты сравнения;

Таблица 1

Результаты сравнительного анализа эффективности реализаций метода между языками программирования Lisp и Python

ЯП/ Интерпретатор	Время выполнения алгоритма / с	Количество занятой памяти / байт
Lisp / CLISP 2.49	1,249	16027792
Python / CPython 3.5	0,324	284236

Важно понимать, что результаты анализа времени выполнения могут иметь погрешности и значительно отличаться, так как зависят не только от используемых интерпретаторов и их настроек, но и от архитектурной и операционной платформы. Представленные результаты были получены при использовании интернет-ресурса: rextester.com. Данный ресурс представляет собой онлайн-сервис по запуску и выполнению алгоритмов, написанных на различных языках программирования. При этом вычисления осуществляются на едином сервере с одинаковыми настройками интерпретаторов и единой архитектурной и операционной платформой. На сер- вере установлены процессор Intel Xeon E5-2640v3 (2.60GHz) и операционная система Linux (версия ядра 4.4.0 64bit SMP). Для проверки и сравнения результатов рекомендуется использовать ресурс1, 2. Также отметим, что все исходные коды алгоритмов доступны в публичном репозитории на сайте github [8].

Заключение

Из результатов проведенного исследования следует, что оригинальный метод, лежащий в основе анализируемой системы логикоматематического моделирования, является универсальным и воспроизводимым, как на языках функционального программирования, так и на императивных языках. В результате исследования модифицированная реализация метода на языке императивного программирования Python оказалась более эффективной. В связи с высокой популярностью языка Python разработка и оптимизация указанной реализации наиболее целесообразна.

Перспективы модификации рассматриваемой системы и ее алгоритмов заключаются в том, что на их основе в будущем можно будет построить вопросно-ответные, экспертные, рекомендательные системы поддержки принятия решений, замещающие собой зарубежные аналоги.

В качестве рекомендаций по методике дальнейшего анализа и оптимизации алгоритмов системы на основе полученных результатов, можно предложить следующее:

• •    провести асимптотический анализ алгоритмов системы;

• •    осуществить сравнительный анализ производительности алгоритмов с использованием большего количества интерпретаторов;

• •    провести оптимизацию алгоритмов на языке Python, используя методы структурного синтеза, модификацию кода и инструментальные средства PyPy, Numba и LLVM.