Анализ эффективности метода нелокального улучшения в задачах оптимального управления

Теория оптимального управления развивалась во многих научных школах, включая отечественные, которые внесли значительный вклад в ее становление. Было разработано множество численных и приближенных методов решения задач оптимального управления, которые продолжают развиваться по разным направлениям (A.B. Аргучинцев, A.C. Булдаев, В.И. Гурман, В.А. Дыхта, В.И. Зубов, В.Б. Колмановский, В.Ф. Кротов, В.А. Срочко, А.И. Тятюшкин, Р.П. Федоренко, Ф.Л. Черноусько и другие).

В. Ф. Кротов в своей работе [10], описал общий метод глобального улучшения управлений на основе достаточных условий. Близкими к глобальному методу являются так называемые нелокальные методы улучшения в дифференциальных системах, разрабатываемые в работах В.А. Срочко и А.С. Булдаева.

Методы нелокального улучшения в отличие от локальных методов (например, метода условного градиента) не используют операцию слабого или игольчатого варьирования управления на каждой итерации с параметрическим поиском улучшающего управления (который является довольно трудоемким) в достаточно малой окрестности улучшаемого управления.

Нелокальное улучшение в различных классах задач оптимального управления опирается на точные формулы приращения целевых функционалов, т.е. на формулы без остаточных членов разложения. В результате получается улучшающая последовательность, которая может быть минимизирующий, на основе которой можно построить приближенное решение задачи.

А.С. Булдаев и В.А. Срочко в [3, 4, 5, 8] получили результаты для нелинейных, линейных, линейно-квадратичных и полиномиальных по состоянию задач оптимального управления, обладающие свойством нелокального улучшения управлений с использованием специальных сопряженных систем и краевых задач. Эти подходы дают возможность улучшать неоптимальные управления, удовлетворяющие принципу максимума, включая особые управления. А.В. Аргучинцев в работе [1] точные формулы приращения использовал для поиска решения задач оптимального управления гиперболическими системами.

В работе проводится численный анализ сравнительной эффективности новых модификаций нелокальных методов улучшения с использованием точных формул приращения для общих нелинейных задач [4].

• 1.    Постановка задачи

Будем рассматривать задачу оптимального управления со свободным правым концом:

x (t ) = f (x (t), u (t), t), x (10 ) = x 0, u (t)g U, t g T = [t0,t1 ], t1

Ф(u) = ^(x(t1)) +JF (x(t),u (t), t) dt ^ inf, t0

где x ( t ) g R" - вектор состояния, u ( t ) g R^r - вектор управления. В качестве допустимых управлений рассматривается множество V кусочно-непрерывных на [ t 0 , t₁ ] функций со значениями в выпуклом компактном множестве U с R^r . Промежуток управления [ t 0 , t₁ ] и начальное состояние x 0 заданы.

Аналогично [3] предполагаются выполненными следующие условия:

• 1)    функция ф ( x ) непрерывно-дифференцируема на R ” , вектор-функции F ( x , u , t ) , f ( x , u , t ) и их производные F_x ( x , u , t ) , F_u ( x , u , t ) , f_x ( x , u , t ) , f_u ( x , u , t ) непрерывны по совокупности аргументов ( x , u , t ) на множестве R ” x U x T ;

• 2)    функция f ( x , u , t ) удовлетворяет условию Липшица по x в R ” x U x T с константой L >  0 || f ( x , u , t )^{- f} ( y , u , t )||< Lx ^- y ||.

Эти условия гарантируют существование и единственность решения x ( t , v ) , t g [ 1 0 , t₁ ] системы (1) - (2) для любого допустимого управления v ( t ) , t g [ 1 0 , t 1 ] .

Решать поставленную задачу (1) – (3) будем при помощи модифицированного проекционного метода нелокального улучшения управлений с дифференциально-алгебраической сопряженной системой [3, 4, 5]. Этот метод не содержит операцию выпуклого или игольчатого варьирования управления на каждой итерации улучшения.

Введем функцию Понтрягина

H (p, x, u, t ) = ( p, f (x, u, t)}- F (x, u, t), где p (t, u, v) - сопряженная переменная.

Для допустимого управления u g V и фиксированного параметра а > 0 рассматривается проекционное отображение ua (p,x,t) = Pu (u(t) + aH (p,x,u,t)), t g[10,t1 ], где PU – оператор проектирования на множество U в евклидовой норме.

Дифференциальный принцип максимума (ДПМ) в задаче (1) - (3) для управления u g V с помощью отображения uα представляется в виде u (t ) = ua (p (t, u, v), x (t, u), t), t g[ 10, t1 ], а > 0.(4)

Для выполнения ДПМ достаточно проверить условие (4) хотя бы для одного а >  0 .

Далее рассмотрим дифференциально-алгебраическую сопряженную систему [4, 5]:

p(t) = -Hx (p(t),x(t),w(t),t)-r(t), p (t1 ) = -^x (x (t1))-q,

H ( p ( t ) , y ( t ) , w ( t ) , t ) ^- H ( p ( t ) , ^x ( t ) , w ( t ) , t ) =

(Hx ( p ( t ) , x ( t ) , w ( t ) , t ) + r ( t ) , У ( t )- x ( t )) ,

ф( y (t1))- ф( x (t1 )) = (^x (x (t1))+q, y (t1)-x (t1)).

Величины r (t) и q всегда можно выразить из соответствующих алгебраических уравнений (7) и (8) (возможно и не единственным образом) [4, 5]. Такая модификация сопряженной системы позволя- ет получить [5] формулу приращения целевой функции в задаче (1) – (3) , которая не содержит остаточных членов разложений.

Если в задаче (1) - (3) f ( x , u , t ) , F ( x , u , t ) линейны по x , то из [4, 5] следует, что r ( t ) = 0 , а если ф ( x ) линейна, то q = 0 .

Пусть дифференциально-алгебраическая сопряженная система допускает решение p ( t , u , v ) , t g [ t 0 , t 1 ] для допустимых управлений u , v при w ( t ) = u ( t ) , x ( t ) = x ( t , u ) , y ( t ) = x ( t , v ) . Таким образом, решив систему (5) - (8) можно однозначно определить отображение P ( u , v ) = p ( t , u , v ) , t g [ 1 0 , t 1 ] на множестве V x V (возможно, не единственным образом).

Применим метод проекционных возмущений [4], где в качестве параметра возмущения рассматривается параметр проектирования а >  0 .

v(t) = Pu (u(t) + а(Hu (p(t,u,v),x(t,v),u(t),t) + 5(t))), t g T.(9)

• 5 ( t ) находится из алгебраического уравнения

H ( p ( t , u , v ) , x ( t , v ) , v ( t ) , t ) - H ( p ( t , u , v ) , x ( t , v ) , u ( t ) , t ) =

( Hu (p (t, u, v), x (t, v) , u (t) , t) + 5 (t), v (t)- u (t )} .(10)

Невозмущенное условие получается из возмущенного (9) - (10), при а = 0 , которое имеет тривиальное решение v ( t ) = u ( t ) , t g [ 1 ₀, t 1 ] .

Итерационный процесс решения задачи (9) – (10) имеет вид vk+1 (t) = Pu (u0 (t) + a(Hu (p (t, u0, vk), x (t, vk), u0 (t), t) + 5 (t))),(11)

H ( p ( t , u ⁰, v k ) , x ( t , v k ) , v k ( t ) , t ) - H ( p ( t , u ⁰, v k ) , x ( t , v k ) , u ⁰ ( t ) , t ) =

HHu (p(t,u0,vk),x(t,vk),u0 (t),t) + 5(t),vk (t)-u0 (t^, t G T,(12)

где u ⁰ g V - начальное приближение. 5 ( t ) выражается из (12), причем, при вычислении 5 ( t ) надо учесть некоторые условия:

• 1.    Если все компоненты v k ( t ) = u ⁰ ( t ) , то алгебраическое уравнение (12) выполняется тождественно. В этом случае компоненты 5 ( t ) могут принимать произвольные значения, тогда полагаем значения всех компонент 5 ( t ) = 0 ;

• 2.    Если, хотя бы одна компонента вектора v k ( t ) ^ u ⁰ ( t ) , то полагаем значения всех остальных компонент 5 i ( t ) = 0 . Тогда для этой компоненты однозначно определяется соответствующая компонента 5 ( t ) из формулы (12).

В случае линейной по управлению задачи (1) - (3) полагаем 5 ( t ) = 0 , t g T . [4, 5].

Итерационный процесс для расчета дифференциально-алгебраической сопряженной системы (5) – (8) представляется в форме:

pk+1 (t) = — Hx (p+1 (t),x0 (t),u0 (t),t)-r(t),(13)

pk+1 (t1 ) = -Фх (x 0 (t1))- q,

H ( p k ( t ) , x^k ( t ) , u ⁰ ( t ) , t ) - H ( p k ( t ) , x ⁰ ( t ) , u ⁰ ( t ) , t ) =

HHx (pk (t), x0 (t), u0 (t), t) + r (t), xk (t)- x0 (t )^ ,(15)

p( xk (ti))- Ц x0 (ti)) = ^Px (x0 (ti))+q, xk (ti)- x0 (ti)).           (i6)

где p k ( t ) = p ( t , u °, v k ) , x k ( t ) = x ( t , v k ) .

Вычисляя r ( t ) и q из уравнений (i5) - (i6) также необходимо учитывать некоторые условия:

• i.    Если все компоненты x k ( t ) = x ⁰ ( t ) , то алгебраическое уравнение (15) выполняется тождественно. В этом случае компоненты r ( t ) могут принимать произвольное значение, тогда выбираем значения всех компонент r ( t ) = 0 . Также, если в конечный момент выполняется x k ( t_i ) = x ⁰ ( t _i ) , уравнение (16) обращается в тождество, поэтому задаем q = 0 для всех компонент;

• 2.    Если, хотя бы одна компонента вектора x k ( t ) ^ x ⁰ ( t ) , соответствующая компонента r ( t ) однозначно определяется для этой компоненты из формулы (15) при условии равенства нулю остальных компонент. Если при этом t = t _i , то соответствующая компонента для q определяется из уравнения (16) при условии равенства нулю остальных компонент.

• 2.    Вычислительный эксперимент

В случае линейной по управлению задачи (i) - (3) полагаем r ( t ) = 0 , t е T , q = 0 . [4, 5].

Вычислительный эксперимент проводится на известных задачах в плане их численного решения тем или иным методом.

В примерах вычисленные значения управляемых, фазовых и сопряженных переменных запоминались в узлах равномерной сетки с шагом дискретизации At = i0-3 на отрезке [10, ti ]. В промежутках между соседними узлами сетки значение управления принималось постоянным и равным значению управления в левом узле. Численный расчет задачи проводился до первого улучшения. Далее строи- лась новая задача, и итерационный алгоритм повторялся. В качестве критерия остановки выбиралось условие |ф( uk+i ) — Ф( uk )|-|ф( uk )|'£, где £ > 0 — заданная точность (в примерах £ = Ю-4). Эф- фективность методов также зависит и от алгоритмов, используемых для решения вспомогательных задач, например, интегрирование дифференциальных систем. Численное решение фазовых и сопряженных задач Коши осуществлялось методом Рунге-Кутта-Вернера пятого или шестого порядка точности с помощью библиотеки IMSL языка Fortran PowerStation 4.0 [2]. За единицу трудоемкости, аналогично [3, 7], взято решение задачи Коши отдельно для фазовой и сопряженной системы. Сравнительный анализ методов решения проводится по суммарному количеству задач Коши.

Пример 1. Рассмотривается задача, связанная с оптимизацией некоторого химического аппарата [9] (стр. 255 – 263). Данная задача также рассматривалась в работе [7].

x ( t ) = —( ki ( u ) + k2 ( u ) + k3 ( u )) xi, xi ( 0 )= i,

< x2 (t) = ki (u)xi -k4 (u)x2,            x2 (0) = 0, x3 (t) = k4 (u)x2 -k5 (u)x3,             x3 (0) = 0.

u ( t ) е [ 0,823 ] , t G [ 0,i ] . Ф ( u ) = - x ₃ ( i ) ^ min.

Система дифференциальных уравнений описывает реакции, протекающие в смеси трех веществ, где x; (t), г = i, 2,3 - их концентрация. Первым веществом является сырье, второе - промежуточный продукт, а третье - окончательный результат. Управление u (t) является температурой, от которой зависят интенсивности реакции.

Функции kt (u), из системы дифференциальных уравнений, имеют вид k (u) = Ci exp

E_ ( J1 )

R I 658 u ^J

i = 1, ^ 5 ,

Данный вид характерен для химической кинетики.

Значения постоянных (аналогично [7, 9]) равны

C 1 = 1.02 , C 2 = 0.93 , C ₃ = 0.386 , C 4 = 3.28 , C ₅ = 0.084 , R = 1.9865 , E 1 = 16000 , E 2 = 14000 ,

E ₃ = 15000 , E ₄ = 10000 , E ₅ = 15000 .

В [9] данная задача решалась при помощи метода проекции градиента (МПГ), в [7] – методом условного градиента (МУГ) и методом условного квазиградиента 1-го порядка (МУК – 1), т.е. методами градиентного типа. В данной работе проводится расчет при помощи нелокального метода улучшения.

Для решения задачи введем необходимые конструкции.

Функция Понтрягина для заданной задачи записывается следующим образом:

H (p, x, u, t) = - p1 [ k1 (u) + k2 (u) + k3 (u )] x1 +

+ P 2 [ k ( u ) x — k ₄ ( u ) x ₂ ] + P 3 [ k ₄ ( u ) x ₂ - k ₅ ( u ) x 3 ] .

Градиенты:

^Hx , = — P 1 [ ^k 1 ^{+ k} 2 ^{+ k} 3 ] ⁺ P 2 ^k 1 , ^Hx 2 = — P 2 ^k 4 ⁺ P 3 ^k 4 , ^Hx 3 = — P 3 ^k 5 •

^Hu = ^- P 1 x 1

Z d.( u )

i = 1

+ p ₂ x 1 d 1 ( u ) - p ₂ x ₂ d ₄ ( u ) +

+ p ₃ x ₂ d ₄ ( u ) - p ₃ x ₃ d 5 ( u ) ,

, / x ^dki ( ^u ) E _{z x} , где d ( u ) =---- =-^L = —i^k ,. ( u ) , г = 1, ^ ,5 .

ⁱ du Ru ^{2 i}

Так как в данной задаче f ( x , u , t ) , F ( x , u , t ) и ф ( x ) линейны по x , значит дифференциальноалгебраическая сопряженная система сведется к стандартной

P1 (t) = P1 [ k (u) + k2 (u) + k3 (u)] - p 2 k1 (u), P1 (1) = 0, p 2 ( t ) = P 2 k4 ( u )- P 3 k4 ( u ) , P 2 (1) = 0,

^P 3 ( t ) = P 3 ^k 5 ( u ) , P 3 ( 1 ) = ^{1 .}

Итерационный процесс (11) – (12) для рассматриваемой задачи выглядит следующим образом: u^{k + 1} ( t ) = ^Pu ( u ⁰ ( t ) ⁺ « ( ^Hu ( P^k ( t ) , x k ( t ) , u ⁰ ( t ) , t ) ⁺ ^ ( t ) ) ) ,

^{5 (} t )

H ( p^k ( t ) , x^k ( t ) , u^k ( t ) , t ) - H ( p^k ( t ) , x^k ( t ) , u ° ( t ) , t u^k ( t ) - u ⁰ ( t )

• -Hu ( Pk ( t) , xk ( t ) , u 0 ( t ) , t ) .

k = 0,1,2, _ .

Здесь x^k ( t ) и p^k ( t ) - решение фазовой и сопряженной системы, соответственно, на k -ой итерации метода. 5 ( t ) вычисляется, соблюдая условия описанные выше.

В качестве начального приближения выбиралось управление u ⁰ ( t ) = 600 . В таблице 1 приводятся результаты, полученные рассматриваемым методом (ПМНУ), при различных значениях параметра а , и методами из [7, 9] (МУГ, МУК - 1, МПГ) ( Ф * обозначает наилучшее значение функционала). Для МПГ не указано число задач Коши, в связи с тем, что Р. П. Федоренко в [9] не вводил критерий трудоемкости.

Сравнительный анализ эффективности

	ф	Число задач Коши
МУГ	-0.43620	876
МУК – 1	-0.43682	215
МПГ	-0.435	---
ПМНУ ( а = 10 4 )	-0.43735	47
ПМНУ ( а = 10 3 )	-0.43558	155
ПМНУ ( а = 10 5 )	не сходится	---

Таблица 1

При дальнейшем уменьшении параметра возмущения возрастает количество решенных задач Коши и падает точность значения функционала. При увеличении параметра возмущения до а = 10 5 (и выше) ПМНУ не сходится.

На рисунках 1 и 2 показаны итоговое значение управления (рисунок 1) и фазовые траектории (рисунок 2) решения задачи, рассчитанные модифицированным проекционным методом нелокального улучшения.

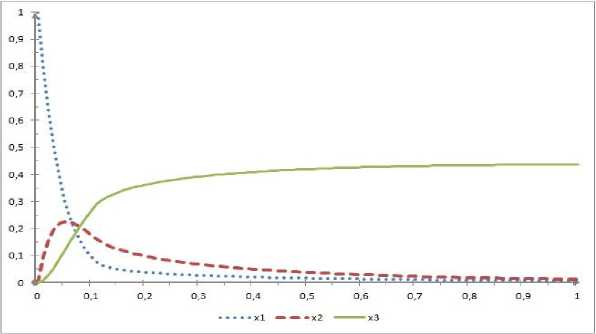
Рис. 2. Фазовые траектории

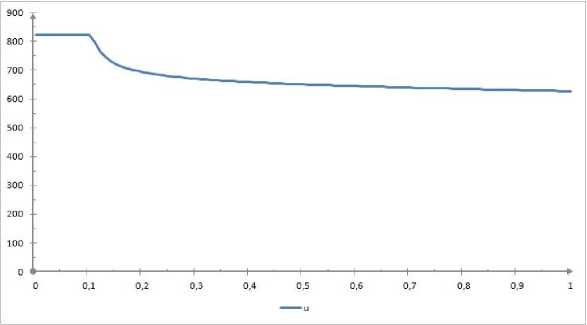
Рис. 1. Управление

Пример 2. Рассмотривается задача оптимального управления шаговым электродвигателем [3,7]. x ( t ) = x 2 ,

< x ₂ ( t ) = - ax ₂ — b

•       \         (. 2n i ■ У 2n u1 sin (2x1) + u2 sin I 2x1 + — I + u3 sin I 2x1 - — x3 (t) = x2 + k1 u1 + k2u2 + k3u3.

x 1 ( 0 ) = ^П , x ₂ ( 0 ) = 0, x 3 ( t ) = 0

u i ( t ) e [ 0,16 ] , i = 1,2,3, t e [ 0,0.05 ] .

ф ( u ) = x ₃ ( 0.05 ) ^ min.

Здесь x 1 ( t ) - положение вала двигателя, x ₂ ( t ) - его скорость, x ₃ ( t ) - требование стабилизации электродвигателя. Управления u 1 ( t ) , u ₂ ( t ) , u ₃ ( t ) соответствуют квадратам токов в обмотках. Требуется минимизировать функционал, т.е. привести положение вала к нулю при минимальных затратах.

Значения параметров (аналогично [3, 7]) равны k.= 0.001, i = 1,2,3; a = 50, b = 1000.

В [7] данная задача решалась с помощью метода условного градиента (МУГ) и методами условного квазиградиента 1-го и 2-го порядка (МУК – 1, МУК – 2), в [3] с помощью метода проекционных возмущений условия оптимальности (МПВУО). В данной работе сравниваются результаты, полученные этими методами, с результатами модифицированного проекционного метода нелокального улучшения.

Аналогично примеру 1 введем необходимые конструкции.

Функция Понтрягина:

H ( p , x , u , t ) = p 1 x ₂

—

г       I                  I p2 ax2 + b I u 1 sin (2x1) + u2 sin I 2x1 +I +

V        V                      V

. । _    2 n IY

+ p ₃ ( x 1 ² + k 1 u 1 + k ₂ u ₂ + k ₃ u ₃ ) .

+ u 3 sⁱⁿ I 2 x ^— — I I

V 3 222

Градиенты:

H x 1

-

2                   2        2        2

I           2 n 1 I

■ 2 bp ₂ u 1 cos ( 2 x 1 ) + u ₂ cos I 2 x 1 +--I + u ₃ cos I 2 x 1

V                   V ^{3 2}         2

-

2 π

^{+ 2} P 3 x 1 ^Hx ₂

= p 1 ^{— a} p 2 ,

H = 0,.

x ₃

Г     2n 1

H„ = — bPi sin (2x,) + k, Px, H„ = — bp3 sin 2x + — + Lp,, H„ = — bp. sin2

u1            2             1        1 3 u2            2             1      3          2 3      u3            21

2n ] ,

^— "3 l ^{+ k} 3 ^p 3 .

Составим дифференциально-алгебраическую сопряженную систему ( q = 0 , так как ф ( x ) линейна по x ):

j I                  \              I . 2n i             I 2n p1 = 2bp21 u1 cos (2x1) + u2 cos I 2x1 + — I + u3 cos I 2x1 ——

^{— 2} p 3 ^x 1 ^— r 1 ( t )

p 2 = ap 2 — p1 — r2 (t) , p 3 = — r3 (t) , p1 (0.05) = 0, p2 (0.05) = 0, p3 (0.05) = —1,

—

где r ( t ) определяется из уравнения (15):

r ⁽ ‘ )

H(p (t),xk (t),и° (t),t)-H(pk (t),x° (t),и° (t),t xk (t)- x0 (t)

)

• - H^(p^k ( t ) , x ⁰ ( t ) , и ⁰ ( t ) , t ) , г = 1,2,3 .

При его вычислении необходимо учитывать условия, описанные выше. x^k ( t ) и p^k ( t ) - решение фазовой и сопряженной системы, соответственно, на k -ой итерации метода Применим итерационный процессе (11) - (12), где 5 ( t ) = 0 , так как задача линейна по управлению. В качестве начального приближения возьмем управление u ⁰ ( t ) = 0 , i = 1,2,3 .

В таблице 2 приведены результаты, полученные для различных параметров α в методах МПВУО [3] и ПМНУ, и результаты, полученные методами из [7] (МУГ, МУК - 1, МУК) ( Ф обозначает наилучшее значение функционала).

Таблица 2

Сравнительный анализ эффективности

	Ф	Число задач Коши
МУГ	0.00817	617
МУК – 1	0.00988	410
МУК – 2	0.00792	287
пмну ( а = 10 2 )	0.00779	309
мпвуо ( а = 10 2 )	0.00779	309
пмну ( а = 150 )	0.00778	229
мпвуо ( а = 50 )	0.00783	593
пмну ( а = 50 )	0.00784	477

Уменьшая параметр возмущения до а = 10 в методе ПМНУ получаем значение функционала Ф = 0.00794 при трудоемкости 243 задачи Коши (при дальнейшем уменьшении возрастает количество решенных задач Коши и падает точность значения функционала). При увеличении параметра возмущения до а = 200 (и выше) ПМНУ не сходится.

Полученные значения управления и фазовых траекторий изображены на рисунках 3, 4 и 5. Итоговое управление и ₂ = 0 и на рисунках не представляется.

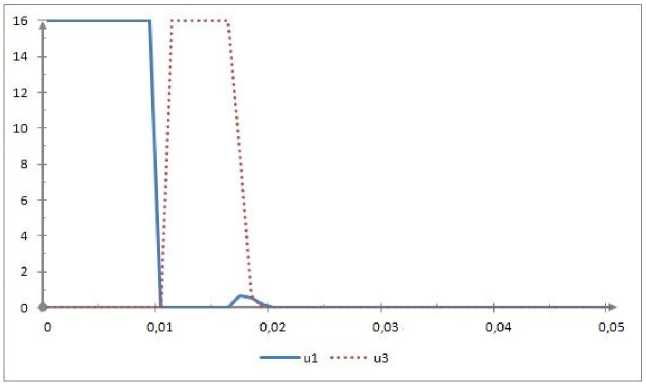
Рис. 3. Управления

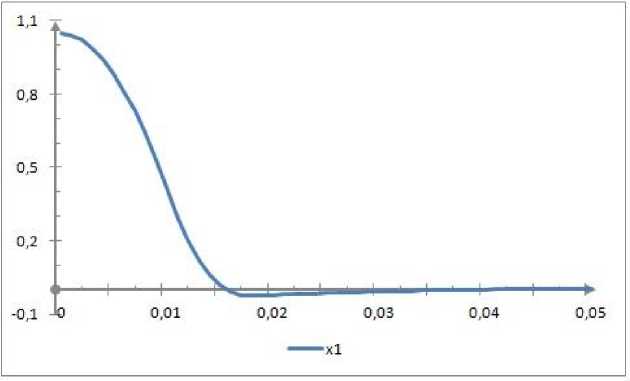
Рис. 4. Фазовая траектория X 1 ( t )

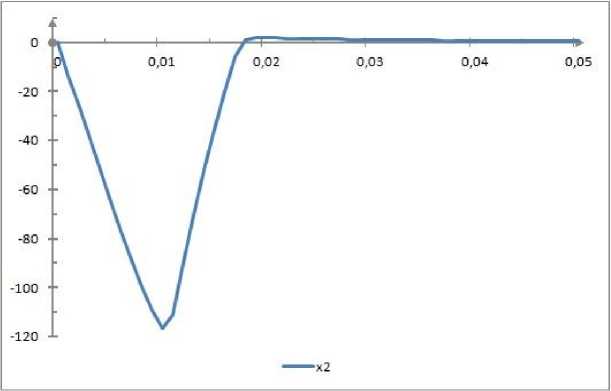
Рис. 5. Фазовая траектория X 2 ( t )

По таблице 2 видно, что для параметра а = 150 (экспериментально подобранного) ПМНУ оказывается более эффективным, так как он дает лучшее значении функционала, затрачивая при этом меньшее число задач Коши. При сравнение ПМНУ с МУГ, МУК -1, МУК – 2 видно, что значение функционала, полученное ПМНУ меньше значения функционала для других методов. Таким образом, сравнительный анализ показывает, что рассматриваемый метод является эффективным и по трудоемкости, и по значению целевого функционала.

Заключение

Традиционно для решения задач оптимизации применяются градиентные процедуры [6, 9], в которых в общем случае релаксация по функционалу обеспечивается лишь локально. Методы возмущений не гарантируют релаксацию функционала на каждой итерации, но компенсируют это отсутствием операции параметрического поиска. Нелокальность улучшения обеспечивается фиксированностью параметра возмущения. Данное свойство (нелокальность улучшения) при поиске решения является существенным фактом повышения эффективности. Проведенные численные расчеты продемонстрировали в рамках рассматриваемых задач повышенную эффективность нелокальных методов по сравнению с градиентными процедурами.

О.Р. Козлова. Применение метода вектор-функций Ляпунова к задаче нормирования воздействий