Анализ эффективности распараллеливания популяционных методов оптимизации с помощью прокси-приложений

Актуальным подходом к решению многомерных задач непрерывной оптимизации является применение популяционных методов оптимизации [1], к которым относятся эволюционные алгоритмы – генетические, метод дифференциальной эволюции, и роевые – метод роя частиц, алгоритм бактериального поиска и т.д. Практически все алгоритмы данного класса устроены по одной общей схеме: имеется популяция фиксированного размера отдельных особей, представляющих возможные решения оптимизационной задачи, которые выполняют коллективный поиск искомого глобального экстремума. Ключевым моментом такого поиска оказывается взаимодействие особей популяции, при этом разные алгоритмы реализуют разные схемы взаимодействия, эмулируя тот или иной аспект коллективного поведения соответствующего биологического или физического прототипа. Несмотря на существующее разнообразие алгоритмов указанного класса, при организации взаимодействия

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №3, 2018 год внутри популяции все они оперируют достаточно ограниченным числом паттернов взаимодействий, комбинируя их тем или иным способом.

Отличительной особенностью популяционных алгоритмов является их высокая вычислительная сложность, которая во многих важных приложениях еще усугубляется сложностью вычисления целевой функции, подлежащей оптимизации [2]. С другой стороны, все эти алгоритмы в силу своей природы обладают высокой степенью встроенного параллелизма, т.к. большая часть операций в них выполняется параллельно или над отдельными особями (оператор мутации в генетических алгоритмах), или над парами особей (оператор скрещивания). Перечисленные факты делают популяционные методы оптимизации практически идеальным объектом для реализации на параллельных вычислительных системах [3]. Ограниченный список паттернов взаимодействия делает возможным выполнение автоматического распараллеливания заданного популяционного алгоритма под заданную модель параллельного выполнения. Такая задача и является конечной целью настоящего исследования. Целями же данной работы являются:

• -    выделение, классификация и формализация паттернов взаимодействия между особями популяции;

• -    разработка средств высокоуровневого описания популяционных алгоритмов для решения задач непрерывной оптимизации;

• -    программная реализация разработанного подхода, позволяющая полностью автоматически генерировать для заданного алгоритма оптимизации программу на языке C++ с учетом указанной пользователем модели выполнения;

• -    разработка прокси-приложений, эмулирующих работу популяционных алгоритмов оптимизации, и исследование с помощью их эффективности распараллеливания данных алгоритмов.

• 2.    Модель популяционных алгоритмов оптимизации

Исследование структуры популяционных методов непрерывной оптимизации проводилось на следующем наборе алгоритмов: генетические алгоритмы, метод роя частиц, метод CSO , муравьиные алгоритмы, алгоритм бактериального поиска, алгоритм пчелиного поиска, гравитационный алгоритм. Предполагается, что данные, с которыми работает популяционный алгоритм, распределены между особями популяции и представлены атрибутами особей, скалярными или векторными, например, положение и скорость частицы в методе PSO . Общие для всех особей данные представлены атрибутами среды. В результате проведенного анализа были выделены следующие паттерны взаимодействия между особями популяции:

• -    FOREACH f – применение оператора f ко всем особям популяции. Примеры: оператор мутации в генетическом алгоритме, обновление состояния (положения и скорости) в методе роя частиц.

• -    PAIRWISE f – случайное разбиение популяции на пары и применение оператора f к каждой составленной паре. Примеры: операторы отбора и скрещивания в генетическом алгоритме, турнирный оператор в методе CSO.

• -    REDUCE key global – семейство паттернов, выполняющих редукцию (минимум, максимум, сложение и т.п.) атрибута особей key в глобальное значение (атрибут среды) global . Примеры: определение лучшего решения в популяции в методе PSO, поиск центроида популяции в алгоритме CSO.

• -    ROULETTE key – реализация отбора по атрибуту key с помощью метода рулетки. Примеры: отбор (в том числе ранговым методом) в генетических алгоритмах и алгоритме бактериального поиска.

• -    DISTANCE pos f key – вычисление для каждой особи популяции суммы значений функции f , примененной к расстояниям до всех других особей. Положение особи задается атрибутом pos , вычисленная сумма сохраняется в атрибуте key . Примеры: процедура роения в бактериальном поиске, вычисление сил в алгоритме гравитационного поиска.

Также в число паттернов были включены дополнительные паттерны взаимодействия со средой с учетом возможной параллельной реализации такого рода алгоритмов, например:

• -    LOAD global - ввод данных (атрибутов среды).

• -    SAVE global - вывод данных.

• -    COPY id key global - копирование атрибута key особи с идентификатором id в атрибут global среды.

• 3.    Программная реализация

Помимо перечисленных выше паттернов в модель были добавлены вспомогательные команды, задающие списки атрибутов особей ( LOCALS ) и среды ( GLOBALS ), и управляющие команды ( BEGIN , END , BEGINLOOP , ENDLOOP ). Примеры описания генетического алгоритма и метода CSO в рамках предложенной модели приведены на рис. 1 (модификатор * перед именем атрибута означает, что данный атрибут является векторной величиной).

GLOBALS f_min LOCALS *х, f BEGIN FOREACH init BEGINLOOP FOREACH eval PAIRWISE select PAIRWISE cross FOREACH mutate ENDLOOP MIN f, f_min save f_min END

GLOBALS *g, f_min LOCALS *x, *v, f BEGIN FOREACH init BEGINLOOP FOREACH eval MEAN X, g PAIRWISE compete FOREACH update ENDLOOP MIN f, f_min save fmin END

Рис. 1. Описание генетического алгоритма (слева) и алгоритма CSO (справа)

На основе предложенной модели была разработана программная система для автоматической генерации кода определенного пользователем популяционного алгоритма для заданной им модели параллельного выполнения. На вход системе поступает описание алгоритма, состоящее из двух частей. В первой части описывается структура алгоритма в терминах перечисленных выше паттернов (как это показано на рис. 1). Во второй части пользователь определяет (на языке C ++) содержание используемых им операторов, например, для генетического алгоритма - это операторы init , eval , select , cross и mutate . Такое высокоуровневое описание алгоритма преобразуется в готовую к компиляции программу на языке C ++. Для организации такого преобразования возможны два принципиальных подхода. При первом подходе оно реализуется средствами целевого языка ( C ++) с использованием специальных библиотек шаблонных функций. При втором подходе такое преобразование выполняется отдельной программой (препроцессором), которая использует описание пользователя как шаблон для генерации целевой программы. В настоящей работе был реализован второй вариант в силу его большей гибкости, кроме того, такой подход позволяет строить более компактный и более оптимальный код, что должно положительно сказываться на его эффективности.

Программа-препроцессор была написана на языке Python. При ее вызове пользователь, помимо кода своего алгоритма, указывает и целевую модель выполнения. В настоящее время система поддерживает три модели выполнения (рис. 2):

• -    SEQ - генерируется последовательная программа;

• -    ISL - генерируется параллельная программа с использованием технологии MPI на основе островной модели популяционных алгоритмов;

• -    SUB - субпопуляционная модель, в которой популяция разбивается на отдельные субпопуляции одинакового размера, каждая из которых обрабатывается одним процессорным узлом, также с использованием MPI.

• 4.    Разработка прокси-приложений

Рис. 2. Модели параллельного выполнения (слева направо): островная, субпопуляционная, master-slave и клеточная

В дальнейшем планируется расширить список моделей выполнения клеточной моделью ( CEL ) и моделью Master-Slave ( MAS ). Кроме того, предполагается предоставить пользователю дополнительную возможность использования технологии OpenMP .

Описанная модель и ее программная реализация были протестированы на трех популяционных алгоритмах: генетическом алгоритме, методе роя частиц и методе CSO . Система выдает корректный (готовый к компиляции и выполнению) код на языке C ++ в трех моделях выполнения (последовательная, островная и субпопуляционная) по одному и тому же описанию алгоритма. Важным свойством предложенного подхода является компактность описания алгоритмов оптимизации, которое оказывается в 3-4 раза короче окончательного кода этого же алгоритма на C ++ (см. табл. 1).

Таблица 1. Сравнение размера (в строках) исходного и сгенерированного кода для трех алгоритмов и трех моделей выполнения

	Source	SEQ	ISL	SUB
Генетический алгоритм	61	175	204	244
Метод роя частиц	60	183	212	270
Метод CSO	65	188	217	257

Описанную выше модель популяционных алгоритмов оптимизации можно модифицировать для генерации прокси-приложений, эмулирующих работу соответствующего метода оптимизации. Выполнение такого прокси-приложения будет зависеть от ряда параметров, включая стандартные (размерность задачи, размер популяции и т.п.) и дополнительные, которые будут определять время выполнения каждого оператора данного алгоритма. Отметим, что в рассматриваемом подходе к распараллеливанию каждый оператор (например, eval ) представляет собой, по сути, атомарную операцию, ее наиболее важным количественным свойством оказывается как раз время ее выполнения. Такая параметризация прокси-приложения позволит относительно легко производить исследования по эффективности распараллеливания того или иного алгоритма, а также выполнять настройку аппаратных свойств целевой параллельной вычислительной системы для наиболее оптимального выполнения этого алгоритма.

В качестве примера такого исследования был выполнен анализ эффективности параллельной реализации субпопуляционной модели распараллеливания в зависимости от числа операций (вычислительной сложности) в операторе eval – вычисление целевой функции, подлежащей оптимизации. Заметим, что большинство алгоритмов рассматриваемого класса использует в своей работе разного рода глобальные операции, которые снижают эффективность их параллельной реализации. Примером такой глобальной операции является паттерн PAIRWISE, работа которого подразумевает полное перемешивание популяции. Если вычислительная составляющая алгоритма невелика (например, в случае простой целевой функции низкой размерности), то существенная часть времени при параллельном выполнении алгоритма (например, генетического) будет расходоваться именно на организацию перемешивания, которая в текущей реализации сводится к сортировке популяции по случайному ключу. Однако в ряде приложений [2] вычисление целевой функции может оказаться настолько сложным, что временем выполнения всех остальных операторов и паттернов можно будет пренебречь. В последнем случае эффективность распараллеливания должна приближаться к единице.

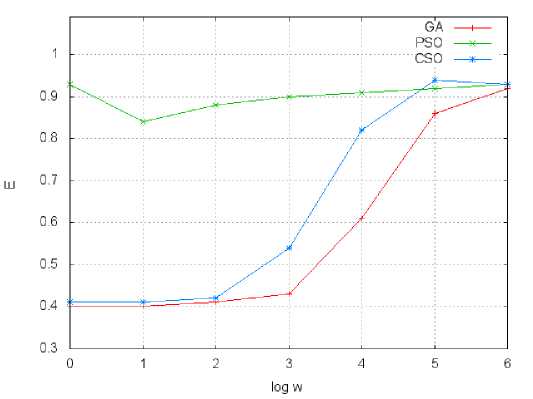
Рис. 3. Зависимость эффективности распараллеливания E от вычислительной сложности w оператора eval

Для проверки этой гипотезы был проведен численный эксперимент, в котором варьировалось только время вычисления целевой функции в операторе eval . Результаты этого исследования приведены на рисунке 3. По горизонтальной оси графика отложен десятичный логарифм числа операций умножения в целевой функции (на одну размерность задачи). По вертикальной оси – эффективность (ускорение, деленное на число процессорных элементов). В данном случае использовались 4 процессора. Хорошо видно, что генетический алгоритм и алгоритм CSO , в которых применяется перемешивание популяции, демонстрируют предсказанное поведение. В то же время алгоритм PSO , в котором из глобальных операций используется только редукция, показывает слабую зависимость эффективности параллельной реализации от вычислительной сложности оператора eval .

Заключение

В результате выполненной работы получены следующие результаты:

• -    выполнена классификация и формализация паттернов взаимодействия особей популяции на основе анализа наиболее популярных популяционных алгоритмов оптимизации;

• -    предложена модель организации популяционных алгоритмов оптимизации, на основе которой разработан метод высокоуровневого описания таких алгоритмов для решения задач непрерывной оптимизации;

• -    выполнена программная реализация предложенной модели, позволяющая пользователю по его исходному коду алгоритма полностью автоматически генерировать код параллельной программы с учетом выбранной им модели параллельного выполнения;

• -    разработан метод построения параметризованных прокси-приложений, эмулирующих параллельное поведение рассматриваемых популяционных алгоритмов;

• -    проведено численное исследование эффективности параллельной реализации трех алгоритмов в зависимости от вычислительной сложности оператора, реализующего вычисление целевой функции.