Анализ контактного динамического взаимодействия клубня картофеля с поверхностью

Цель работы: проанализировать напряженное состояние, возникающее в мякоти клубня при ударных нагрузках и на основании этого определить предельные высоты падения и скорости соударений клубня, не вызывающие разрушения клеток мякоти и, следовательно, ее потемнения.

Выбор представительного объема. Для определения напряжений, возникающих в мякоти клубня при ударе, воспользуемся представлениями классической механики твердого деформируемого тела, в которой предполагается, что деформируемые тела, испытывающие действие внешних сил, являются сплошными, однородными и изотропными и что самый малый элементарный объем, выделенный из этого тела, обладает теми же физикомеханическими свойствами, что и все тело. Для клубня элементарный объем может быть представлен в виде совокупности клеток. Объем этой совокупности клеток должен быть в тысячи раз меньше объема клубня и его физико-механические свойства должны представлять собой осредненные значения свойств основной ткани клубня. Объем одного клубня имеет порядок 10² см³. Выберем величину представительного объема 1 мм³, что в среднем в 10⁵ раз меньше объема клубня. Данный представительный объем будет состоять из 10⁴ клеток и может достаточно адекватно отражать свойства мякоти. Выбор такого элементарного представительного объема позволит считать материал клубня сплошным, однородным и изотропным и оправдывает применение для решения данной динамической контактной задачи математической модели механики сплошной среды.

Рис. 1. Разрыв тонопласта и потемнение мякоти:

1 - клеточная оболочка, 2 - вакуоль, 3 - цитоплазма, 4 - ядро

Теория упругого удара Герца [2]. Введем следующие допущения: 1) клубни имеют сферическую форму; 2) характерные размеры области контакта малы по сравнению с размерами каждого из контактирующих тел и с радиусами кривизны их поверхностей; 3) поверхности контактирующих тел предполагаются гладкими; 4) трение отсутствует; 5) клубни абсолютно упруги. Данные допущения позволяют применить для анализа напряженного состояния теорию упругого контакта Герца. Эта теория является квазистатической в том смысле, что деформации считаются сосредоточенными в окрестности области контакта и определяются статической теорией: волновым движением в телах пренебрегается и предполагается, что каждое тело движется в любой момент времени со скоростью его центра масс.

Пусть два упругих шара с массами m 1 и rr m2 движутся со скоростями Vz и V2z вдоль линии, соединяющей их центры, и сталкиваются в точке O. Во время удара из-за упругих деформаций центры шаров приближаются друг к другу на расстояние 5z. Согласно теории Герца, соотношение между силой взаимодействия шаров P и 5z берется таким, как при статическом контакте

— —-- 1--

R R R ₂

E * - приведенный модуль упругости:

1 1 - V2 1 - V2 — —--L +--- e * e    e2

В формулах (3) и (4) соответственно: R 1 , R 2 -радиусы шаров, E 1 , E ₂ и v 1 , v ₂ - модули упругости и коэффициенты Пуассона тел. Максимальное сближение шаров 5 _z, соответствующее максимальной их деформации, то есть когда d5_z / dt=0

f —

z

I 4 K J

где V , - скорость сближения тел в момент удара, m - приведенная масса, определяемая выражением

— — — + —

P — KS3,2

z

В выражении (1) K - коэффициент, зависящий от упругих свойств тел, а также их размеров:

Выражение (1), а следовательно и (5) справедливы для случаев, когда область контакта имеет форму круга, то есть в случае контакта двух тел сферической формы и при контакте сферы с плоскостью. Радиус круговой площадки контакта:

K — ⁴ R ^т E *

a —

,

n p 0 R 2 E *

где R - приведенный радиус, определяется выражением

где p ₀ - максимальное давление (в центре площадки контакта). Максимальное давление p 0 определяется по формуле

= f 6P ^ 3 2na2 l n3R2 J

m

R ³

mm l m + m 2 J

f RR 2

⁴ ^ R³ P i ' ^{R 3 P} )

3 l R 3 p + R 2 P 2 J

f R i R ₂

В связи с тем, что при ударных взаимодействиях сжимающая нагрузка P зависит от скорости, на практике удобнее пользоваться формулой, которая получается при подстановке в (8) выражений (1), (2), (5) и определяет величину максимального контактного давления в момент максимального сжатия в зависимости от скорости удара V 0 :

l R i + R 2 J

l R i + R 2 J

( 2)

p0

1

n

30 m3 V02E*4 R

J

где R , ρ , R 2 , ρ 2 соответственно радиусы и плотности первого и второго тела (клубня). Так как в случае уборки или сортирования картофеля взаимодействовать друг с другом будут в основном клубни одного сорта, а следовательно, одинаковой плотности, положим ρ = ρ 2 = ρ . Тогда выражение ( 2) примет вид

Используем формулу (9) для определения максимального контактного давления при следующих случаях удара.

1. Удар клубня о плоскость. Для этого необходимо в выражениях (3) и (6) положить для плоскости R 2 =∞ и m 2 =∞. Тогда в формуле (9) R и m это будут соответственно радиус и масса клубня (шара), а V 0 – скорость центра масс клубня в момент удара. В этом случае удара m и R не являются приведенными величинами, поэтому массу клубня можно выразить через его плотность ρ :

4 np(Rx + R2 )3 m3          2

R ³ =     R^R 2     ""

Функция f ( R ) принимает максимальное значение при R = R 2 = R . В этом случае

f ( R ) =

m

R ³

16 n

= T ^p

.

( 4)

m = pnR3

3      .            (10)

То есть выражение (9), определяющее максимальное контактное давление будет принимать наибольшее значение, когда радиусы контактирующих тел будут равны. Следовательно из всех возможных комбинаций наиболее опасным будет случай соударения двух клубней одинакового радиуса. Подставив ( 4) в (9) получим выражение для максимального контактного давления в данном случае:

Тогда формула (9) приобретет вид

p

40 p V² l

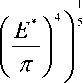
p 0²⁾ =

160 pvО l

f E *

ln J J

,

( 5)

Как следует из формулы (11) при ударе тела сферической формы о плоскую поверхность максимальное контактное давление определяется скоростью удара, упругими характеристиками обоих тел и плотностью шара (клубня) и не зависит от его размеров и массы.

2. Соударение двух свободных клубней. Такая ситуация может возникать, когда клубни сталкиваются друг с другом в воздухе в момент пересыпания или при свободном перекатывании по рабочим поверхностям. В этом случае величины m и R являются приведенными и определяются выражениями (3) и (6). Поэтому в формуле (9) отношение m / R ³ может быть представлено в виде

где ρ – плотность соударяющихся клубней одинакового радиуса.

3. Удар клубня о поверхность из плотно лежащих клубней. Будем считать, что клубень массой m и радиусом R ударяется о клубень (поверхность) конечного радиуса R 2 и бесконечной массы m 2 =∞ (рис. 2). В этом случае согласно формуле (6) m = m , а R будет приведенной величиной и определится выражением (3). Поэтому для данного случая в формуле (9) отношение m / R ³ может быть представлено в виде

m

R ³

m f Ri R2

- nR, p f Ri R 2 '

l R i + R 2 J

l R i + R 2 J

( 6)

В результате преобразований получим m 4пр | R1

R³ "  3 ( R 2

A ³

+ ¹ 7

= f ( R )

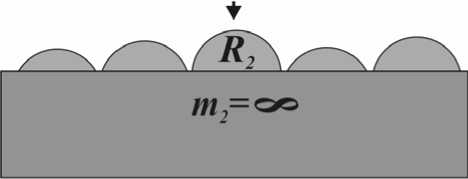
Рис. 2. Падение клубня на несвободный клубень

Величина функции f ( R ) в данном случае будет зависеть от соотношения радиусов k = R 1 / R 2 .Чем больше будет значение k , то есть чем больше радиус падающего клубня по сравнению с радиусом поверхности в точке контакта, тем больше будет функция f ( R ), а следовательно, тем будет больше контактное давление. Формула (9) для контактного давления для этого случая примет вид

p

40 ( k + 1 ) 3 p V ²

V

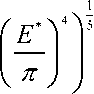
где ρ – плотность падающего клубня.

Напряжения в окрестности площадки контакта. Согласно теории Герца максимальные касательные напряжения возникают в точке, лежащей на оси контакта, на глубине равной почти половине 0,48 a радиуса a площадки контакта. Для рассмотренных выше случаев соударения эта точка находится на глубине 3-5 мм от поверхности клубня. На рис. 3 показано распределение эквивалентных напряжений в окрестности круговой площадки контакта радиуса a , вычисленных по теории Треска-Сен-Венана. Скорее всего, именно напряжения σ экв =0,62 p 0 над площадкой контакта вызывают разрушения клеток и, как следствие, потемнение мякоти внутри клубней при ударах.

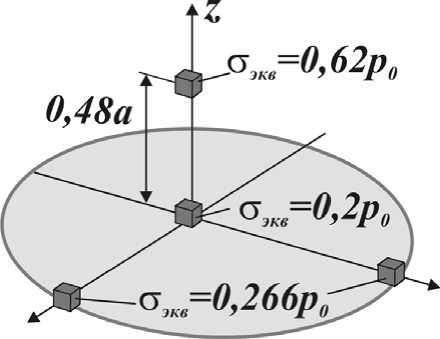
Рис. 3. Эквивалентные напряжения в окрестности площадки контакта

Результаты экспериментального определения характеристик жесткости и прочности мякоти клубня при сжатии. Для определения эквивалентных напряжений, возникающих в окрестности площадки контакта, а также для оценки прочностных свойств мякоти клубня необходимо знать упругие и прочностные характеристики мякоти. Программа экспериментальных исследований включала в себя определение модуля упругости и предела прочности мякоти клубня при сжатии [3]. Сжатие образцов мякоти производилось на устройстве, созданном на базе прибора для измерения твердости металлов и сплавов по методу Роквелла (ТК-14-250). Схема устройства представлена на рис. 4. На стол 1 прибора ТК-14-250 был установлен динамометр 2 с пределом измеряемых усилий от 2 до 200 Н. Два индикатора часового типа А с ценой деления 0,01 мм, прикрепленные к динамометру, отградуированы для измерения усилий. Наличие двух индикаторов необходимо, чтобы контролировать отсутствие перекоса упругого элемента при сжатии образца. На площадку динамометра устанавливается образец 3 . Винт 4 служит для подвода образца к наконечнику 5 и для последующего сжатия образца. Наконечник соединен с пружиной 6 , величина сжатия которой измеряется индикатором В с ценой деления 0,002 мм. Величину перемещения рабочего стола измеряет индикатор С , цена деления которого 0,01 мм. Сжатие образца осуществляется за счет перемещения вверх рабочего стола. Величина сжимающего усилия определяется по показаниям индикаторов динамометра.

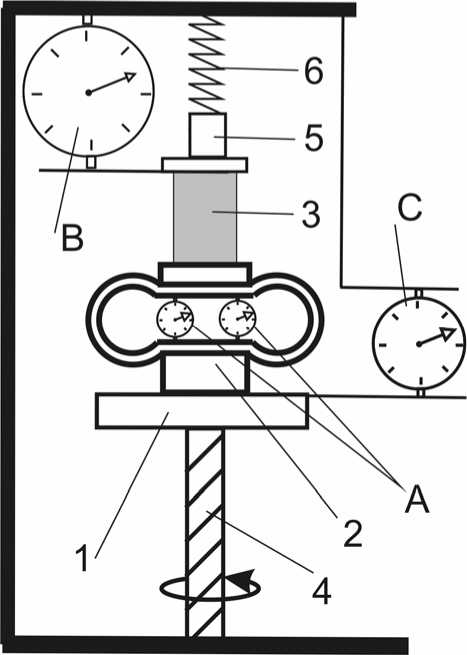
Рис.4. Схема устройства

Испытания проводились на образцах, вырезанных из мякоти клубней сорта Невский. Из мякоти клубней вырезались образцы цилиндрической формы при помощи специальных приспособлений-шаблонов диаметрами 8,6 мм, 12 мм, 14,8 мм, высотой 10-16мм. Образцы вырезались в различных направлениях в основном из области коры и внешней сердцевины. Скорость деформирования поддерживалась в пределах 0,3-0,5 мм/мин с помощью секундомера. По показаниям индикатора А с помощью градуированной таблицы определялась на каждом шаге величина нагрузки Р (кг), по показаниям индикаторов А , В , С определялась величина абсолютной деформации образца Δ l (мм). В дальнейшем на каждом шаге вычислялись величина напряжения σ и относительной деформации ε . Относительные погрешности определения σ и ε в среднем составили около 1%. По построенной диаграмме деформирования σ - ε определялся модуль упругости и предел прочности образца.

На рис. 5 представлена диаграмма деформирования образца, вырезанного из клубня в области коры и начала внешней сердцевины. Как видно из графика, диаграмма деформирования до предела прочности практически линейная. Здесь же показана ее линейная аппроксимация методом наименьших квадратов, дано уравнение аппроксимирующей прямой и величина достоверности аппроксимации R2. Величина модуля упругости tgα для данного образца, как следует из уравнения прямой E=2,7 МПа, а предел прочности – σв=0,83 МПа.

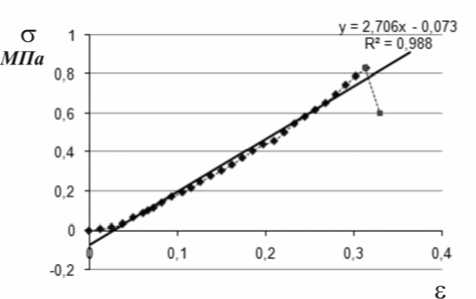
Рис. 5. Диаграмма деформирования образца

На рис. 6 представлены диаграммы деформирования нескольких образцов вырезанных из области коры и внешней сердцевины по различным направлениям. Как видно из представленных графиков, диаграммы деформирования образцов различаются незначительно. Пределы изменения модуля упругости Е=2,2-3,08 МПа, предела прочности σ в =0,7-0,96 МПа. Представленная на графике прямая является линейной аппроксимацией одной из диаграмм деформирования.

В ходе проведения эксперимента определялась плотность мякоти. Пределы изменения плотности получились ρ =1119-1163 кг/м³, что соответствует справочным данным. В результате проведенных испытаний для дальнейших расчетов можно принять в среднем для мякоти клубней картофеля сорта Невский: модуль упругости – Е =2,6 МПа, предел прочности – σ в =0,83 МПа, плотность – ρ =1140 кг/м³.

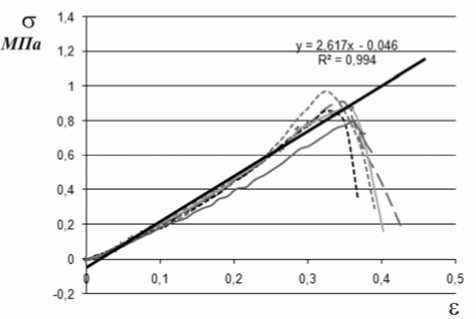
Рис. 6. Диаграммы деформирования нескольких образцов

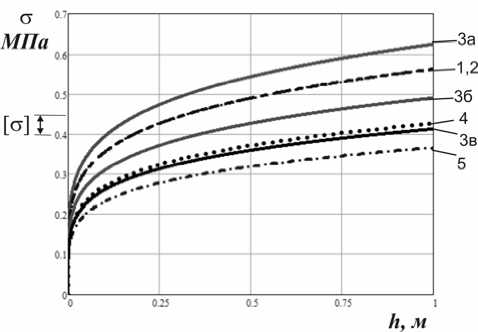
Рис. 7. Зависимость эквивалентных напряжений от высоты падения клубня на различные поверхности: 1 – сталь, 2 – дерево, 3 (а, б, в) – несвободный клубень, 4 – свободный клубень, 5 – резина.

Таблица 1. Допускаемые высоты падения и скорости удара клубня

Поверхности	Высота падения, м	Скорость удара, м/с
сталь, дерево	0,18-0,33	1,9-2,5
несвободный клубень:
k = 2	0,1-0,2	2,7-3,6
k = 1	0,37-0,66	2,7-3,6
k = 0,5	0,87-1,6	4,1-5,2
резина	1,6-2,8	5,6-7,5
свободный клубень	-	3,8-5

Результаты расчета допускаемых высот падения клубней. Зависимость эквивалентных напряжений в опасной точке внутри клубня от высоты падения на различные поверхности показана на рис. 7. Напряжения при падении на стальную и деревянную поверхности отличаются незначительно (графики 1 и 2). При падении клубня на несвободный клубень напряжения зависят от отношения радиусов клубней k = R 1 / R 2 . График 3а соответствует k =2, график 3б построен для k =1, график 3в – для k =0,5. При соударении двух свободных клубней (график 4) рассмотрена ситуация, когда радиусы соударяющихся клубней одинаковы. График 5 соответствует падению на поверхность, покрытую резиной. При расчете предельных высот падения допускаемые напряжения были взяты в пределах |σ|=0,4-0,5 МПа. Результаты расчета приведены в таблице 1.

Вывод: полученные результаты можно использовать для совершенствования технологии уборки и сортирования картофеля.