Анализ контактного взаимодействия искусственного видеотактильного механорецептора с мягкими биологическими тканями

В настоящее время методы компьютеризированной тактильной диагностики, основанные на применении тактильных сенсоров, начинают использоваться при проведении медико-биологических исследований и в лечебной практике [4, 5]. В основе экспериментальных методик диагностики и мониторинга различных заболеваний, использующих тактильные сенсоры, лежит определение в реальном времени физико-механических характеристик патологических тканей, которые отличаются от тканей здоровых. Актуальность проблемы создания искусственных тактильных механорецепторов – систем искусственного осязания, близких по своим функциям к осязательным функциям человека, связана с необходимостью использования в современной медицинской практике неинвазивных методов диагностики различных заболеваний. Принципиальным преимуществом здесь обладает пальпация, не связанная с воздействиями на биологическую ткань проникающих излучений или ультразвука. Искусственный тактильный механорецептор может оказаться достаточно эффективным средством неинвазивной экспресс-диагностики состояния мягких биологических тканей вне специализированных клиник. Кроме того, механорецептор позволяет проводить наблюдение за ходом различных медицинских лечебных процедур в реальном времени.

Принцип работы искусственных механорецепторов основан на анализе процесса контактного взаимодействия [1, 3], который позволяет оценить различия отклика на механическое воздействие здоровой и больной тканей и идеологически близок методу индентирования, широко используемому в механике деформируемого твердого тела.

В литературе известны несколько конструктивно различающихся схем, реализующих работу искусственных механорецепторов [4]. Основное отличие известных и разрабатываемых искусственных тактильных датчиков заключается в устройстве чувствительного элемента, а также специфике методов получения и обработки информации. Так, например, в работе [6] описан метод определения механических характеристик мягких тканей, основанный на применении жестких инденторов различной формы. Изменение формы поверхности исследуемого образца фиксировалось с помощью трехмерных оптических систем, а усилия измерялись силовыми датчиками. Исследуемая ткань моделировалась гиперупругой или линейной вязкоупругой средой. При этом задачи идентификации моделей ткани решались путем минимизации различия результатов компьютерного моделирования и экспериментальных данных, измеряемых в процессе индентирования.

Сравнение жесткостей больной и здоровой печени человека, проведенное методом индентирования в условиях живого организма ( in vivo ) [7], показало, что больной орган может существенно отличаться по жесткости от здорового. Так, например, модуль Юнга больной печени оценивается величиной порядка 740 кПа, а здоровой – 270 кПа [7].

Кроме индентирования используются и другие виды нагрузок, прикладываемых на поверхности мягких тканей, такие как вакуумная аспирация, сдвиговые деформации, двусторонняя сжимающая нагрузка. В работах [11, 12] описан портативный прибор для аспирации ткани, при этом деформации поверхности регистрируются с помощью системы зеркал, установленных внутри вакуумной трубки. С помощью данного прибора проведена оценка деформации тканей, а обратная задача определения механических характеристик ткани решается с помощью конечно-элементного моделирования. Для измерения сдвиговых деформаций биологических тканей разработано торсионное резонирующее устройство ( TRD ) [16], с помощью которого был определен модуль сдвига свиной печени, равный 39,1 кПа. Механизированный эндоскопический захват ( MEG ), описанный в работе [14], позволяет изучить механическое поведение тканей в зависимости от сжимающей нагрузки.

В статье [15] предложен лапароскопический захват, представляющий собой устройство, способное обеспечить искусственную тактильную обратную связь путем измерения распределения давления на одной из опорных поверхностей захвата, содержащей массив тактильных датчиков. Данные с этих датчиков представляются в графическом виде на экране компьютера.

Известно, что тактильные сенсоры различных конструкций используются также в робототехнике в качестве чувствительных элементов манипуляторов, имитирующих процессы осязания или захвата и удержания предметов. Например, в [10] описана работа устройства, в котором в качестве чувствительного элемента применяется деформируемая мембрана с маркерами, нанесенными на её поверхность. В манипуляторе, разработанном в Университете Нагойя, сила захвата предметов контролируется видеотактильным сенсором [13, 17].

В данной работе приводятся результаты исследований, выполненные в рамках совместного российско-тайваньского проекта «Разработка методов диагностики патологии мягких биологических тканей при помощи искусственного тактильного механорецептора и алгоритмов обработки тактильной информации» и Программы фундаментальных исследований президиума РАН, связанные с проектированием чувствительного элемента оптического тактильного датчика [2, 8, 9].

Отечественный и зарубежный опыт показывает (см., например, [13]), что перспективным направлением является использование оптических тактильных датчиков, чувствительным элементом которых является прозрачный упругий слой с набором цветных меток или полос. При контакте упругого чувствительного элемента датчика с исследуемой тканью в процессе деформирования меняются взаимное расположение контрольных меток, а также размеры пятна контакта. Эти изменения фиксируются видеокамерой. Обработка информации о перемещениях контрольных меток и усилиях, возникающих при контактном взаимодействии чувствительного элемента сенсора и биологической ткани, позволяет оценить параметры напряженно-деформированного состояния ткани, включая механические свойства исследуемого образца.

Описание конструкции датчика

Принципиальная схема видеотактильного датчика приведена, например, в [13] и показана на рис. 1.

Видеокамера

Источник света

Акриловая пластина

Чувствительный элемент

Исследуемый объект

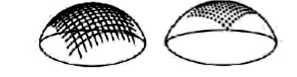
Рис. 1. Основные элементы видеотактильного датчика

ISSN 1812-5123. Российский журнал биомеханики. 2013. Т. 17, № 1 (59): 8–21

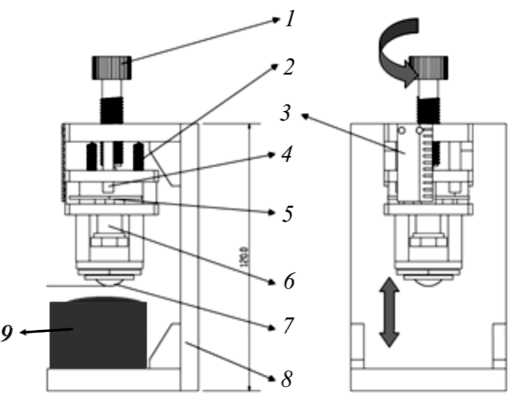
Рис. 2. Установка для испытаний видеотактильного датчика: 1 – ручка настройки;

2 – пружина; 3 – измерительная линейка; 4 – направляющие; 5 – видеокамера;

6 – линзы; 7 – чувствительный элемент; 8 – штатив; 9 – исследуемый объект

В процессе контакта исследуемой ткани с чувствительным элементом сенсора происходит его деформирование и образование зоны контакта, что фиксируется видеокамерой. Чувствительный элемент видеотактильного сенсора изготавливается из оптически прозрачного материала, например, силикона. Конструктивная схема установки, на которой проводились испытания датчика [8, 9], представлена на рис. 2.

Для выбора источника света и его положения было проведено специальное исследование [9]. Форма, размеры и механические характеристики индентора должны подбираться так, чтобы параметры его деформированного состояния можно было бы измерить, а усилия, вызывающие деформацию головки сенсора, не являлись травматическими. Поэтому необходимо провести исследования, направленные на определение оптимальных параметров чувствительного элемента датчика (индентора). Данная проблема может быть изучена методами механики контактных взаимодействий твердых деформируемых тел (см., например, [1, 3]).

Постановка контактной задачи

В процессе разработки датчика рассматривалось два варианта конструкции индентора – головки датчика: в виде сплошного шарового сегмента ( solid type ) и толстой полусферической оболочки ( hollow type ), изготовленных из прозрачного силикона ( PDMS – полидиметилсилоксан). Геометрические размеры двух типов инденторов приведены на рис. 3. Радиусы кривизн внешней поверхности двух типов головки датчика совпадают.

В зависимости от концентрации отвердителя модуль упругости используемого материала PDMS меняется в диапазоне E 1 = 300-2100 кПа (здесь и в дальнейшем индексом 1 будем отмечать характеристики индентора, а индексом 2 – характеристики материала, контактирующего с ним). В расчетах материал индентора и материал, имитирующий мягкую биологическую ткань, предполагались упругими и несжимаемыми; коэффициент Пуассона принимался v i = v 2 = 0,5 (0,49999 - при численных расчетах).

Как указывается в [5], для определенного класса задач допускается моделирование мягких биологических тканей линейно-упругим несжимаемым материалом. Наличие патологических изменений биологических тканей связано с появлением уплотнений,

Чувствительный элемент

===F^ Материал: PDMS

Модуль Юнга: £" = 200-2100 кПа

Полый индентор Сплошной индентор

Единица измерения: мм

Рис. 3. Варианты конструкции индентора (головки сенсора) и используемые материалы т.е. областей, имеющих более высокий модуль Юнга, чем здоровая биологическая ткань. В расчетах принимались следующие значения модуля Юнга для моделирования мягких биологических тканей: E2 = 20 кПа, E2 = 60 кПа и E2 = 100 кПа.

Оценить возможность применения двух вариантов индентора заданной геометрии для целей диагностики патологий мягких тканей можно на основе анализа решения соответствующих контактных задач. Задачи решались численно (в программном коде ANSYS ) в осесимметричной постановке. Геометрически биологическая ткань моделируется цилиндром, радиус и высота которого существенно превышают радиус индентора. Нижнее основание цилиндра закреплено. Индентор и упругое основание расположены соосно. Требуется оценить величину радиальной (горизонтальной) проекции вектора перемещений внешней поверхности индентора в процессе деформирования под действием распределенной направленной по нормали нагрузки, приложенной к его верхней части. Данная компонента вектора перемещений является определяющей при фиксации изменений взаимного расположения меток, нанесённых на внешнюю поверхность индентора.

Задача о контакте сплошного упругого сегмента с упругим ПОЛУПРОСТРАНСТВОМ

Для отработки вычислительной схемы метода конечных элементов численно решена модельная задача о внедрении упругого несжимаемого полушара в упругое полупространство. Конечно-элементная дискретизация расчетной области представляет собой регулярную сетку конечных элементов со сгущением в зоне контакта и приведена на рис. 4.

Под действием сжимающей нагрузки формируется пятно контакта, на поверхности которого и в областях, прилегающих к нему, возникает зона повышенных напряжений.

С целью проверки численного алгоритма проведено сравнение численных результатов, полученных при малых внедрениях, с аналитическим решением задачи Герца о контакте двух упругих тел. Согласно этому решению зависимости радиуса пятна контакта a и величины внедрения δ сферического индентора радиуса R от приложенной нагрузки F имеют вид

Таблица 1

Сравнение численных результатов, полученных при внедрениях, с решением задачи Герца

Параметр	Метод решения
	ANSYS	Решение Герца
Радиус пятна контакта a , мм	1,380	1,360
Величина внедрения δ, мм	0,201	0,231
Коэффициент Пуассона	ν 1 = ν 2 = 4,9999
Модуль Юнга, кПа	E 1 = 500, E 2 = 60
Нагрузка F , Н	0,03 Н

Сравнение результатов решения приведено в табл. 1, из которого следует, что численные расчеты, выполненные методом конечных элементов, хорошо согласуются с аналитическими.

Расчеты выполнялись при значении давления на верхнюю границу индентора P = 150 Па, что соответствует нормальной силе F = 0,03 Н. Выбор столь малого значения нагрузки связан с необходимостью удовлетворения предположениям Герца о малости деформаций, а также с тем, что при пальпации внутренних органов врачу приходится быть особенно осторожным, чтобы, например, не нарушить целостность возможных включений. Заметим, что эффективность подобного подхода для малых сил обеспечивает его применимость и для гораздо более широкого диапазона нагрузок.

На рис. 5 представлено распределение нормальных к плоскостям, параллельным недеформированной поверхности основания, главных (сжимающих) напряжений в инденторе и основании при суммарной нагрузке F = 0,03 Н (максимальные контактные напряжения согласно решению Герца p0 =

3 F

2п a2

= 7800 Па , что согласуется

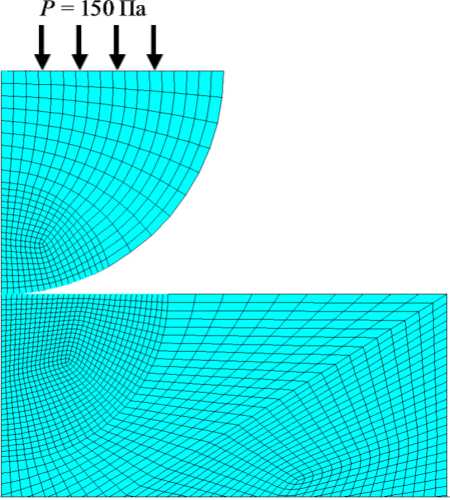
Рис. 4. Конечно-элементная схема, используемая при расчете взаимодействия упругого несжимаемого полушара с упругим полупространством (областью)

5 =

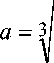
3 FR

4 E ^*

a =э! f ³ f V

R RH 1 4 E

* ^,

где E * - приведенный модуль упругости, E * =

1 -v 2 1 -v 2

\-1

E 1 E 2

.

с результатами расчета).

По результатам счета построены эпюра распределения радиальной компоненты вектора перемещений Ux кругового контура индентора (рис. 6) и график зависимости этой компоненты от длины дуги контура (рис. 7): Ux = Ux (S), где Ux - проекция вектора перемещений на горизонтальную ось (x = r); S - длина дуги окружности профиля индентора.

Расчеты показали, что функция перемещений U x = U x ( S ) является монотонно возрастающей как в пределах пятна контакта, так и вне его. Результаты расчетов показывают, что величина максимальных смещений внутри области контакта не превышает 1 мкм .

Задача о контакте полого сферического индентора с упругим основанием

Для анализа поведения датчика с полой головкой требуется решить задачу взаимодействия сферической оболочки (см. рис. 3) с упругим основанием под действием равномерно распределённой сжимающей нагрузки. В этом случае была использована расчётная схема, приведенная на рис. 8 и представляющая собой регулярную сетку конечных элементов. Размер элементов в зоне контакта подбирался таким образом, чтобы точность определения радиуса пятна контакта составляла более 90% (в данном случае радиус пятна контакта определяется с точностью до четверти длины контактного элемента). Использовались осесимметричные восьмиузловые плоские конечные элементы.

Рис. 5. Распределение нормальных сжимающих напряжений в инденторе и основании при внешнем давлении P = 150 Па ( F = 0,03 Н)

0,0 0,245∙10–6 0,491∙10–6 0,736∙10–6 0,982∙10–6 0,123∙10–5 0,147∙10–5 0,172∙10–5 0,196∙10–5 0,221∙10–5

м

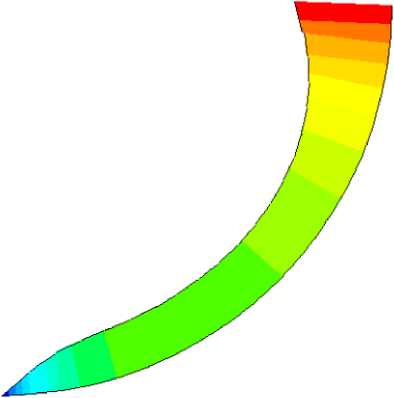
Рис. 6. Эпюра распределений радиальных перемещений по внешнему

контуру индентора

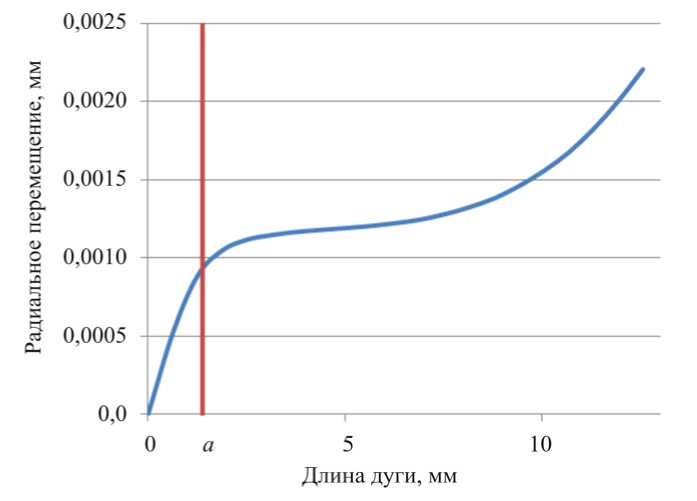
Рис. 7. Распределение компоненты вектора перемещений U x по внешнему контуру индентора ( a – радиус пятна контакта)

На рис. 9 построена картина распределения радиальных напряжений (компоненты тензора напряжений ст xx = ст rr ) в контактирующих телах (в зоне контакта и вне ее): E 1 = 500 кПа для индентора и E 2 = 60 кПа для основания.

Распределения радиальной компоненты вектора перемещений U r ≡ U x по круговому контуру индентора представлены на эпюре (рис. 10, E 1 = 400 кПа) и графике (рис. 11, E 1 = 200 кПа) соответственно.

R in

P = 150 Па

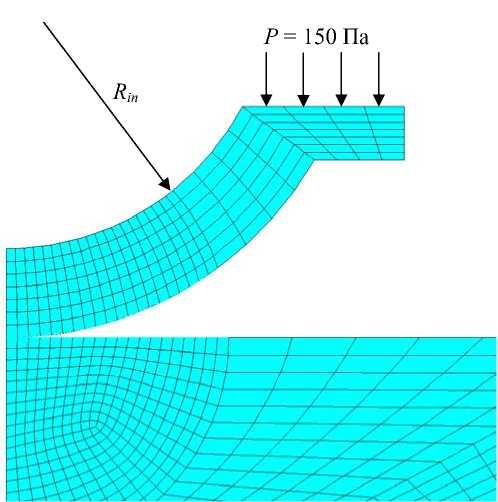
Рис. 8. Схема контактного взаимодействия и конечно-элементная схема

Па

–11522

–9629

–7737

–5844

–3952 –2059 –166 1726 3619

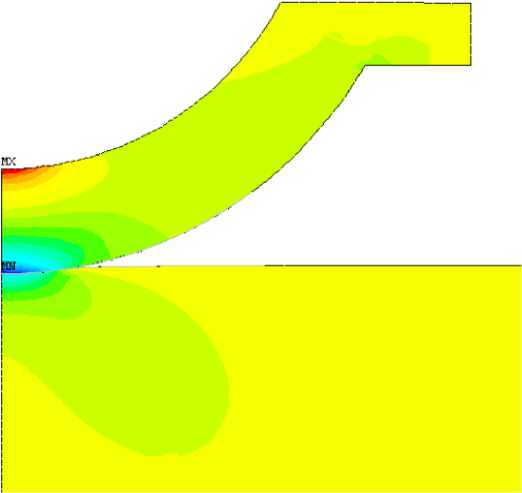
Рис. 9. Распределение радиальных напряжений (компоненты тензора напряжений ст xx = ст rr ) в контактирующих телах

Как следует из результатов, представленных на рис. 10 и 11, под действием приложенной нагрузки происходит деформация индентора таким образом, что на его внешнем контуре в радиальном направлении возникает область сжатия как в пределах пятна контакта (точка a на рис. 11), так и вне его (до точки b на рис. 11). Сжатие кругового контура не является монотонным: в пределах области сжатия радиальные перемещения возрастают от нуля до максимального значения, затем уменьшаются до нуля. Таким образом, на внешней поверхности индентора существует круговой контур, длина которого в процессе деформирования не меняется. Область, лежащая выше этой линии, является зоной монотонного растяжения.

^м    –0,923∙10^–6

1 –0,591∙10–6

–0,260∙10–6

0,714∙10–7

0,403∙10–6

0,734∙10–6

0,107∙10–5

0,140∙10–5

0,173∙10–5

0,206∙10–5

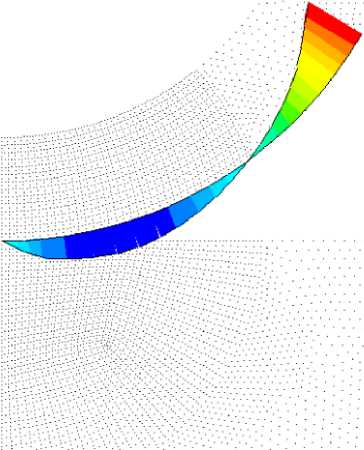
Рис. 10. Эпюра распределения радиальной компоненты перемещений по внешнему контуру индентора

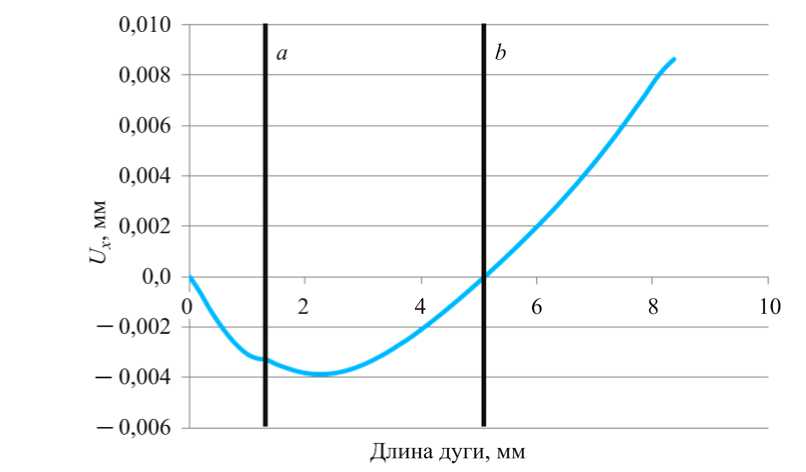
Рис. 11. График распределения радиальной компоненты перемещений по внешнему контуру индентора: a – граница области пятна контакта, b – граница областей сжатия и растяжения

При фиксированных геометрических параметрах индентора выполнены расчеты сформулированной выше контактной задачи для различных марок материала PDMS , из которого изготовлен индентор; модуль упругости рассматриваемых материалов изменялся в диапазоне E ₁ = 200–2100 кПа. На рис. 12 приведены распределения радиальной компоненты вектора перемещений по поверхности полого индентора при разных значениях модуля упругости материала индентора и фиксированном значении модуля упругости основания ( E 2 = 60 кПа). Анализ результатов расчета показывает,

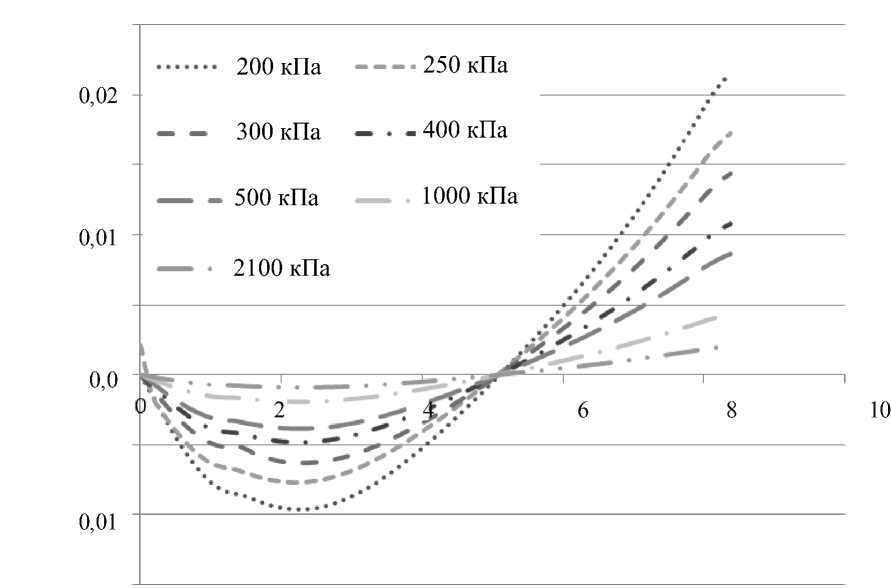
Длина дуги, мм

Рис. 12. Графики распределения радиальной компоненты перемещений по контуру индентора заданной геометрии, но изготовленного из материалов различной жесткости что при уменьшении модуля упругости индентора абсолютные значения радиальных перемещений внутри области контакта возрастают. При выбранном значении внешней нагрузки максимальная величина радиальных перемещений внутри области контакта варьируется в пределах от 1 до 10 мкм в зависимости от модуля упругости индентора (см. рис. 12).

Кроме того, из графиков, построенных на рис. 12, следует, что положение недеформируемого контура на внешней поверхности индентора не зависит от его механических свойств.

На основании выполненных вычислений можно сделать вывод о том, что «чувствительность» метода определения механических характеристик биологических тканей путем нанесения на поверхность индентора рисок, которые смещаются при деформировании ткани в радиальном направлении [13], выше у полого индентора, чем у сплошного, представляющего собой шаровой сегмент (см. рис. 7).

По результатам расчёта задачи о внедрении полого сферического индентора в упругое основание, моделирующее исследуемую ткань, построена зависимость радиуса пятна контакта от модуля упругости материала основания (рис. 13). Расчеты проведены для инденторов, выполненных из силикона с модулями упругости E 1 = 500 кПа и E 1 = 2100 кПа.

Значения радиуса пятна контакта для различных значений модуля Юнга основания и индентора приведены также в табл. 2.

На основании результатов расчетов можно заключить, что радиус пятна контакта возрастает с уменьшением модуля упругости биологической ткани. При этом для биологических тканей с модулем упругости более 50 кПа при внедрении в них полого индентора с модулем упругости 500 кПа площадка контакта больше, чем при внедрении более жесткого индентора (E1 = 2100 кПа), что делает более мягкий индентор предпочтительней при использовании в целях идентификации свойств таких тканей.

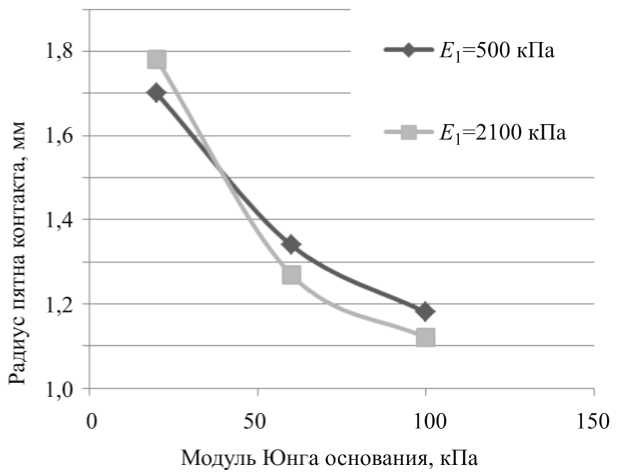
Рис. 13. Зависимость радиуса пятна контакта от модуля упругости материала основания при фиксированном модуле упругости материала индентора

E 1 = 500 кПа и E 1 = 2100 кПа

Таблица 2

Значения радиуса пятна контакта, мм, для различных значений модуля Юнга

Модуль Юнга E 2 , кПа	E 1 = 500 кПа	E 1 = 2100 кПа
20	1,70	1,78
60	1,34	1,27
100	1,18	1,12

Для более мягких биологических тканей (с модулем упругости менее 45 кПа) предпочтительней индентор с модулем упругости E 1 = 2100 кПа. Следует отметить, что материал PDMS , имеющий модуль упругости E 1 = 2100 кПа, отвечает кроме того и требованию максимальной прозрачности, которое необходимо учитывать при изготовлении чувствительного элемента видеотактильного датчика.

Выводы

• 1.    Разработана математическая модель контактного взаимодействия головки сенсора (сплошной и полой) с мягкой биологической тканью, позволяющая оценить характеристики напряженно-деформированного состояния, включая контактные характеристики (радиальные перемещения точек поверхности головки сенсора, размер области контакта, распределение контактных напряжений), которые доступны измерению при индентировании.

• 2.    Проведен анализ распределения перемещений по внешнему контуру головки сенсора (сплошной и полой) и дана оценка величины горизонтальной составляющей вектора перемещений на внешнем контуре и радиуса пятна контакта при различных соотношениях модулей упругости индентора и мягкой биологической ткани.

• 3.    Показано, что наиболее чувствительным к величине перемещений рисок, нанесенных на внешней поверхности головки, является индентор в форме оболочки (тип hollow ).

Полученные результаты могут быть использованы при выборе формы и размера чувствительного элемента видеотактильного датчика, а также при подборе материала для его изготовления.

Благодарности

Работа выполнена при поддержке грантов РФФИ: № 09–08–92003, № 12–01–00800, № 12–08–92005, а также Программы № 25 фундаментальных исследований президиума РАН.