Анализ критического состояния дискретно- неоднородной полосы с наклонной контактной границей и наружным макродефектом в более прочной части

В работе рассматривается НС неоднородной полосы с поверхностным макродефектом в форме наружного разреза или углубления, в более прочной части или на контактной границе, под растягивающей нагрузкой (рис. 1, а ). Граница между более прочной (БП) и менее прочной (МП) частью (контактная граница) прямолинейна, но, как нередко бывает в реальных сварных соединениях, не предполагается ортогональной направлению нагрузки, т. к. существуют различные разделки кромок свариваемых частей с наклонными контактными границами [3, 4] (см. рис. 1, а ). БП часть соединения может испытывать в процессе пластического деформирования ослабляющее влияние МП части. Изучение НС таких неоднородных соединений необходимо для определения прочностных свойств реальных соединений, содержащих наклонные контактные границы и дефекты, поверхностные и внутренние, различной формы и расположения, в сварных конструкциях, в том числе трубах большого диаметра, сосудах давления, соединительных деталях и др. [4-14].

а) б)

Рис. 1: а) варианты расположения дефектов; б) критерий вовлечения БП части соединения в пластическое деформирование в зависимости от угла α и коэффициента K

Математической моделью НС рассматриваемой полосы является граничная задача для системы уравнений пластического равновесия гиперболического типа (при плоской деформации) относительно компонент тензора напряжений. Она, в частности, содержит внутреннее граничное условие на контактной границе и, в общем случае, оказывается переопределенной [1, 15-17]: участки, которые однозначно определяют решения в окрестностях свободной и контактной поверхности, могут накладываться друг на друга. Следствием этого является разрывность решения задачи и негладкость характеристик. Вид и расположение линий разрыва напряжений определяются формой границы и внутренними граничными условиями [1, 15-18].

В работе исследуется критический момент нагружения. Для неоднородных соединений с поперечной менее прочной прослойкой и не очень большой механической неоднородностью он характеризуется началом течения основного металла в приконтактных зонах [4, 17]. Это явление положено в основу создания вычислительной схемы нахождения критической нагрузки в листовых и стержневых образцах и тонкостенных цилиндрических оболочках, содержащих менее или более прочные поперечные прослойки, в том числе с дефектами.

Исследование критических состояний неоднородных соединений в виде полосы с наклонной контактной границей рассматривалось в работах [19-24]. Заметим, что решение задачи сопряжения для напряжений на наклонной контактной границе позволило установить [20, 21, 23] критерий вовлечения БП части соединения в пластическое деформирование в зависимости от угла наклона а и коэффициента механической неоднородности соединения K (рис. 1, б). В работе [25] изучался случай, когда дефект находился в МП части соединения при а = 0.

Цель работы - на основе полного описания полей характеристик, характеризующих критические состояния растягиваемой неоднородной полосы с наружным макродефектом в более прочной части или на контактной границе, при использовании численного решения [21, 23] задачи сопряжения для напряжений на наклонной контактной границе получить алгоритмы для нахождения критической нагрузки, необходимой для разрушения неоднородного соединения в виде полосы в зависимости от его параметров: размеров и расположения дефекта, угла наклона контактной границы а и коэффициента механической неоднородности K .

Всюду в работе верхний индекс «+» указывает на отношение данной величины к БП участку соединения, верхний индекс «-» - к МП участку.

Задача сопряжения для напряжений на контактной границе. Метод нахождения напряженного состояния в различных точках полосы основан на использовании полей характеристик (линий скольжения) участков, находящихся в зоне пластического деформирования. Он в равной мере эффективен для задач растяжения и сжатия [26, 27].

Уравнения равновесия для напряжений на контактной поверхности в безразмерных координатах имеют вид [15-17]:

^ -‘ = K ^ y ; T -y■ = ^КтУ_у - , K = k ⁺/ k" , ⁽¹⁾

где к ⁺ и к ^- - параметры пластичности БП и МП участков соответственно. Здесь ( x '; у ') - декартовы координаты с осью Ox ' , направленной вдоль контактной границы. Безразмерные напряжения получены делением размерных напряжений в БП части на к ⁺ , а в МП части - на к - . Благодаря такой искусственной нормировке различными величинами условие пластичности и, как следствие, система уравнений равновесия с условием пластичности в целом всюду имеет одинаковый вид. Будем называть уравнения (1) условиями сопряжения. После нахождения условных напряжений для вычисления критических нагрузок, определяемых в БП и МП частях полосы, и построения соответствующих эпюр следует вернуться к естественной нормировке, например, делением размерных напряжений на к - всюду в соединении, что равносильно умножению на K напряжений с + и т +у .

Задача сопряжения для напряжений на контактной границе, впервые рассмотренная одним из авторов для плоской контактной поверхности, ортогональной направлению внешней нагрузки, формулируется так: на основе граничных условий и заданных на контактной поверхности условий сопряжения (1) для напряжений найти напряжения с ± и т ±_у на контактной поверхности .

В работах [15-17] показано, что если угол а наклона контактной поверхности к направлению, ортогональному направлению нагрузки, равен нулю, то БП материал начинает течь в критическом состоянии тогда, когда K <  2. В работах [20, 21 ] установлено, что при а Ф 0 начало течения БП материала зависит не только от коэффициента механической неоднородности K , но и от угла а , и найден количественный критерий вовлечения материала БП участка в процесс пластического деформирования. Эта зависимость связана с ограниченностью угла ю ^- поворота характеристик в МП части величиной П 4 — а . С увеличением внешней нагрузки угол ю~ возрастает от нуля до тех пор, пока либо выполняется неравенство

ю" < П 4 — а, либо в какой-то момент БП материал перейдет в пластическое состояние и рост угла ю- прекратится.

Известно [25], что углы поворота характеристик ю - и ю ⁺ связаны с напряжениями на наклонной контактной поверхности уравнениями

с+ = 1 - 2ю+ + cos (2ю+ + 2а), с- = 1 + 2ю + cos (2ю + 2а).

Эти уравнения и условия сопряжения (1) приводят к системе трансцендентных уравнений для нахождения неизвестных ю ^- и ю ⁺ . Представляя неизвестные функции ю ^- и ю ⁺ в виде степенных рядов по параметру 2 = K - 1:

Ш=^ю-^, ю=^ю+2

в уравнения этой системы, можно последовательно находить коэффициенты ю , к = 1,2,3,... Таким образом получены приближенные аналитические выражения для вычисления углов ю ^- и ю ⁺ . Эти выражения, приведенные в [20, 21], имеют в общем случае (когда а Ф 0) громоздкий вид и неудобны для использования. Кроме того, ничего неизвестно о сходимости получающихся рядов. В работах [21, 23] разработан алгоритм численного решения упомянутой системы методом итераций. Написанная на его основе в среде MATLAB программа позволяет вычислять значения углов ю и ю ⁺ на каждом участке контактной границы в зависимости от вида поля характеристик на этом участке.

Напряженное состояние по нетто-сечению в полосе, содержащей в более прочной части поверхностный макродефект. Критическую растягивающую нагрузку можно определять через среднее предельное напряжение c yav по самому слабому сечению. Это сечение - либо нетто-сечение, определяемое положением дефекта в БП части соединения, либо любое сечение в МП части. Обозначим через с у_av - среднее предельное напряжение по нетто-сечению в БП части, проходящее через дно дефекта ортогонально боковой (свободной) поверхности полосы, а через с у_av среднее предельное напряжение в МП части. Здесь

N cr = min ( N cr , N r ) , N r = mK ^ yav , N - = t O - „v .                 (2)

Здесь t - ширина полосы, m - ширина полосы в области дефекта (нетто-сечение), N - - предельное растягивающее усилие для МП части, N_c у - предельное растягивающее усилие для БП части, то есть по нетто-сечению. Критические значения нормальных напряжений о ± вычисляются по формулам [17, 28]:

О = 1 - 2 ю + cos ( 2 ю ) , (3) где в простых однородных полях либо ю = 0, когда характеристики одного из семейств образуют угол П 4 с нетто-сечением, либо ю = Ю , ю = 0, когда характеристики одного из семейств образуют угол П 4 - ю⁺ с нетто-сечением. В веерно-центрированных полях угол ю изменяется от П 4 - ю ⁺ до П 4.

Произвольность угла наклона контактной поверхности и расположения относительно этой поверхности дефекта приводят к большому разнообразию распределений напряжений по нетто-сечению. Существенна не форма дефекта, а положение точки, расположенной на дне дефекта, относительно свободной и контактной поверхности, которое определяется параметрами g и m (рис. 2, 3), а точнее, отношениями gt и mt . На рис. 2 и 3 показаны всевозможные варианты полей характеристик при наличии дефекта с дном в БП части или на контактной поверхности (показаны основные характеристики, определяющие всю картину характеристик).

Случаи, когда a <  0, показаны на рис. 2.

Случай а) – дно дефекта расположено на контактной поверхности. Тогда, в соответствии с (2) и (3),

Ncr = K[(1 -2ю++ cos(2ю+))(m -g) + 2gJ , (4)

N - = 2 1 .

Известно [21], что угол ю ⁺ , как правило, не превышает 0,2 (при | а | - 20 ° ю ⁺<  0,1). Поэтому формулу (4) можно упростить с небольшой ошибкой:

N+ » K [(

2 - 2ю+ - 0,5 (ю+ )2) m + (2ю+ + 0,5 (ю+ )2) g

K [(2 - 2ю+) m + 2ю+ gJ.

Для того чтобы разрушение произошло по нетто-сечению, нужно, чтобы N+r < N„г, то есть чтобы m - — < ю+( m - g).

K

Это имеет место, в частности, если K <  t/m .

Чтобы рассмотреть другие случаи, введем систему координат, приняв за начало координат точку O на дне дефекта, направив ось Оx по нетто-сечению, ось Oy – в направлении БП части.

Для получения приведенных ниже соотношений использовались элементарные соображения из аналитической геометрии.

Случай б) (см. рис. 2). Если дно дефекта расположено достаточно далеко от контактной границы, МП часть не оказывает ослабляющее влияние на БП участок и эпюра напряжений try по- стоянна вдоль контактной линии. Ограничением на этот случай является условие:

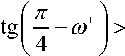
g m - 2 r

где g - mtg lai r =------

i - tg a i

– абсцисса точки пересечения характеристики, проходящей через точку O и линии контакта.

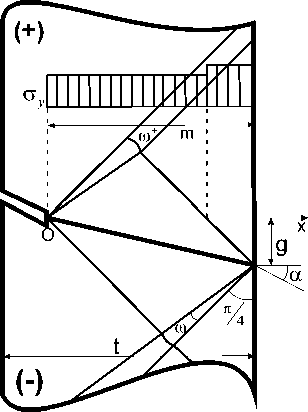
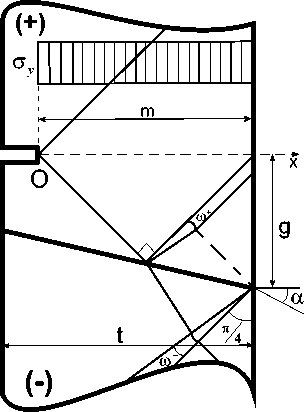
б)

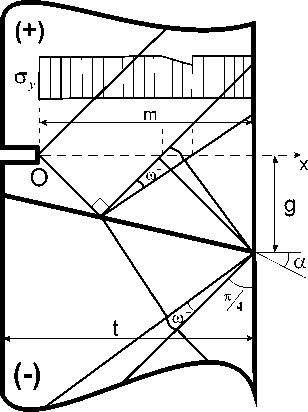
в)

г)

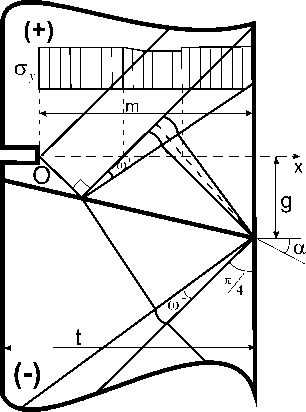
Рис. 2. Схемы полей характеристик и эпюры критических напряжений при отрицательном угле а наклона контактной поверхности: а ) дно дефекта на контактной поверхности; б ) – г ) дно дефекта в БП части соединения: б ) линия разрыва напряжений не пересекает нетто-сечение. Нетто-сечение целиком расположено в простом однородном поле характеристик; в ) линия разрыва напряжений пересекает нетто-сечение внутри угла го ⁺ ;

г ) линия разрыва напряжений пересекает нетто-сечение до пересечения угла го ⁺

В этом случае по нетто-сечению с т = 2 K , поэтому N_c^c_r = 2 Km .Чтобы разрушение произошло по нетто-сечению, требуется, в соответствии с (2), выполнение условия K <  t/m .

Случай в) (см. рис. 2). Ограничением на этот случай является условие:

m - 2 r    п       m - g - r

-------< tgl   c ro+ |<----s----                                      (7)

g      V 4     )      r или, что то же самое,

< tg f п - ro+|<-Л-m - g - r    V 4    )  m - 2 r

а)

О*

x

в)

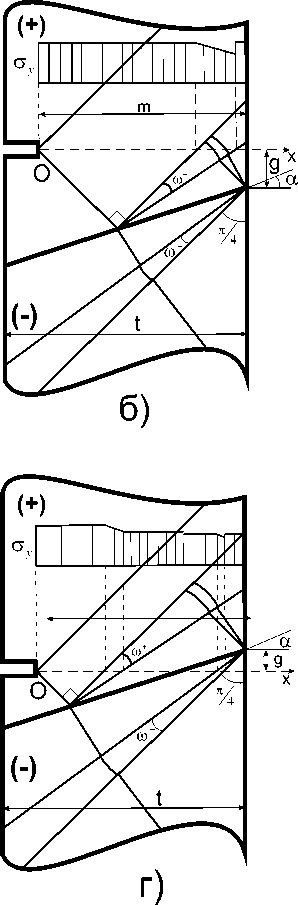
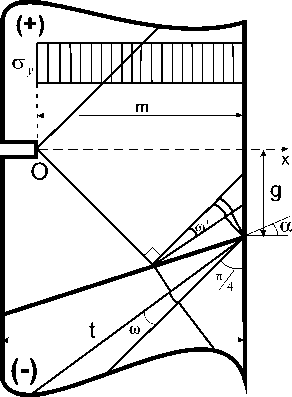
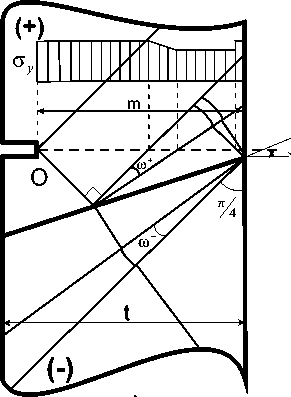
Рис. 3. Схемы полей характеристик и эпюры критических напряжений при положительном угле а наклона контактной поверхности. а ) - в ) нетто-сечение расположено целиком внутри БП части соединения; а ) линия разрыва напряжений не пересекает нетто сечение. Нетто-сечение целиком расположено в простом однородном

поле характеристик; б) Линия разрыва напряжений пересекает нетто-сечение внутри угла ю ⁺ ; в ) Линия разрыва

напряжений пересекает нетто-сечение до пересечения угла ю ⁺ ; г ) нетто-сечение пересекает контактную границу

Здесь, за исключением небольшого промежутка в средней части, длина которого равна ю ⁺ g , по нетто-сечению a = 2 K , а на этом промежутке среднее значение ст, мало отличается от 2 K и вычисляется по формуле

^, = K ( 1 - ю ⁺ + cos ( 2 ю J) .

Поэтому N + ~ 2 Km .

Случай г) (см. рис. 2). Ограничением на этот случай является условие:

I п + 1        r tg I - ю I >----------

V 4     J m - g - r

.

Или, что то же самое,

I n , i m - g - r tg + ю <-------

1 4       J        r

Напряжения о^ по нетто-сечению распределены следующим образом. На правом краю на отрезке длиной g - < у ⁺, до наклонной пунктирной линии на рис. 2, г ), являющейся линией разрыва напряжений [1], о = 2 K . Левее, после разрыва, напряжения снова постоянны: О = K ( 1 — 2 й ⁺ + cos ( 2 ^ + ) ) , на отрезке _2 r + 2 ^ ⁺; m - g - ^ /^. Затем, на отрезке _2 r ;2 r + 2 ^ + ^ они возрастают до о = 2 K и, наконец, в окрестности дна дефекта напряжения снова постоянны: О = 2 K . Поэтому среднее критическое напряжение по нетто-сечению можно представить в виде:

N+г = 2K(2r + й/ )+K(1- 2^+ + cos (2й+))(m - g - 2r) + 2K(g - ®+).

Рассмотрим случаи взаимного расположения нетто-сечения и контактной границы, когда a >  0 (см. рис. 3). Если дно дефекта расположено достаточно далеко от контактной границы, МП часть не оказывает ослабляющее влияние на БП участок, и эпюра напряжений try постоянна вдоль контактной линии. Ограничением на этот случай (см. рис. 3, а ) является условие:

то есть такое же, как в случае рис. 2, б ), где на этот раз абсцисса точки пересечения характеристики, проходящей через точку O , и линии контакта имеет вид:

g + m tg a

1 + tg a

Аналогично, условия реализации случаев рис. 3, б ) и в ) такие же, как в случаях на рис. 2, в ) и г ), то есть определяются формулами (7) и (8) соответственно. По тем же формулам вычисляются критические напряжения на нетто-сечении. Случай рис. 3, г ) исследован в работе [23].

Заключение. В работе дано полное описание случаев взаимного расположения нетто-сечения и контактной границы, приводящих к существенно различным картинам полей характеристик, то есть описаны все случаи, требующие различных вычислительных схем для нахождения критической нагрузки (в работе рассмотрено наиболее важное с точки зрения приложений условие | a | <  П 4). Приведенные аналитические выражения вместе с условиями их реализации, данными также в аналитической форме, позволяют создать несложный алгоритм нахождения критического растягивающего усилия в общем случае расположения дефекта в БП части полосы или на контактной границе, в зависимости от ширины полосы, глубины дефекта, угла наклона и удаленности от дефекта контактной границы и коэффициента механической неоднородности соединения.