Анализ математических моделей низкотемпературного газогенератора с твердым охладителем

Низкотемпературный газогенератор (НТГГ с камерой охлаждения) состоит из камеры сгорания с зарядом твёрдого топлива и камеры охлаждения с гранулами охладителя. При контакте горячих продуктов сгорания топлива с охладителем последний разлагается с поглощением тепла. Температура газа на выходе из НТГГ составляет обычно 370-450 К. Принципиальная схема НТГГ с камерой охлаждения изображена на рис. 1.

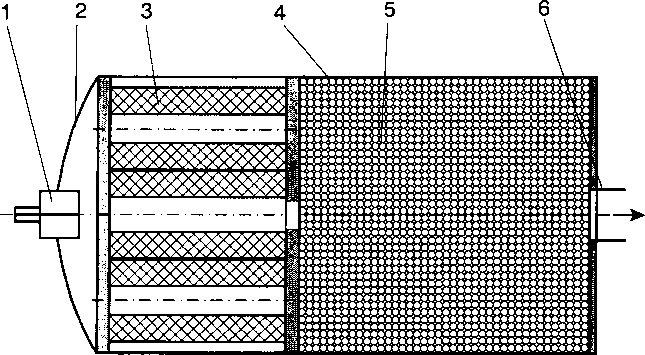
Рис. 1. Принципиальная схема НТГГ: 1 - воспламенительное устройство; 2 - камера сгорания; 3 - заряд твёрдого топлива; 4 - камера охлаждения; 5 - охладитель; 6 - патрубок

Количество топлива и охладителя определяется требованиями потребителя - величиной заполняемого объёма, температурой и давлением газа.

В первом приближении можно считать газовую смесь идеальным газом, подчиняющимся уравнению состояния в виде pV = mRT,                                                                (1)

где т - масса газа в объёме V; р - давление; R - газовая постоянная; Т - температура. В общем случае т = тТ + тх + тв + та.                                                            (2)

Масса воспламенителя тв и масса воздуха та значительно меньше массы топлива тТ и охладителя тх, поэтому в первом приближении можно считать, что т = тТ + тх .                                                                        (3)

Газовая постоянная смеси есть

R = —T-R *^R,.

т

т

Массу охладителя можно найти из уравнения баланса тепла ттбт = шхс„х(7;-Г), где QT - теплотворная способность топлива, ТТ - температура горения топлива. Решая совместно уравнения (1), (5) с учётом (4), найдём массы топлива и охладителя

Шх

Т

R.

рУ

^(jT-T^+R„

т.

Математические модели НТГГ включают в себя математические модели камеры сгорания (КС) и камеры охлаждения (КО). Для описания рабочих процессов в КС применяются термодинамические (нульмерные) и одномерные модели [1]. В КС, применяемых в составе НТГГ, давление по длине меняется незначительно, вследствие чего скорость горения топлива и температура практически не меняются. Поэтому применение нульмерных моделей обеспечивает достаточно высокую точность. .

Первыми математическими моделями КО были нульмерные модели [2]. Такие модели позволяют определить средние в пределах КО значения параметров, но не позволяют учесть особенности процессов тепло- и массообмена. В КО температура по длине меняется от 1600...2000 К до 370.. .450 К. Давление и плотность газа также изменяются в широких пределах. Как показывают экспериментальные данные [3], скорость разложения охладителей существенно зависит от температуры, что оказывает большое влияние на характер протекания процессов в КО.

Нульмерные модели КС и КО включают в себя уравнения баланса массы и энергии смеси газов, уравнение баланса тепла стенок, а также уравнения баланса массы компонентов газовой смеси. В состав газовой смеси в КС входят воздух, водяной пар и неконденсирующиеся продукты сгорания воспламенителя и топлива, такие, например, как углекислый газ, окись углерода и т. п. В состав газовой смеси в КО входят, кроме перечисленных, неконденсирующиеся продукты разложения охладителей. Состояние неконденсирующихся газов в КС и КО с достаточно высокой точностью можно определить по уравнению состояния идеального газа. Для определения состояния водяного пара в КО могут потребоваться уравнения реального газа [4].

Термодинамические модели КС и КО можно записать в общем виде.

dpV               .

7 ^VBX ' ^J m °вых ’ dr

= G_BXh_BX +Q_m- G_BbIxh - Q_n0T;

dx

C_wP_w^Vw ^ ⁼     ” ^Tw ) ^Fw " “„aP ^^W ~ ^Гнар ) ^’HaP ^;

p = pRT.

(Ю)

(П)

В (8)—(12) приняты следующие обозначения: р - плотность; G - расход; h - энтальпия; F - площадь поверхности; Q - тепловой поток; Q_m - источник тепла в КС или сток тепла в КО; а - коэффициент теплоотдачи; c_v - удельная теплоёмкость при постоянном объёме; gj - мас-

Расчет и конструирование

совая доля z-ro компонента газовой смеси; Т - время; J_т - поток массы от сгорания топлива в КС или от разложения охладителя в КО; J_т, - поток массы г-го компонента; индексы: вх - вход; вых - выход; нар - наружный; пот - потери; w - стенка.

Одномерные математические модели КС и КО можно записать в следующем виде.

ЭФ ЭТ

---+---= F , Эт Эх

где

w e = cvT + —.

-nwqw+nQm

Уравнения баланса массы компонентов газовой смеси можно представить в общей форме

dpSgj dGgj

Эт дх ^т’‘ ‘

Уравнение теплопроводности стенки дк = а» д Г ЭТ^ Эт г дЛ dr J

В (13)—(16) w - скорость; ^ - коэффициент гидравлического сопротивления; х - продольная координата; г - радиальная координата; П - эквивалентный периметр; а - коэффициент температуропроводности; S -площадь свободного сечения.

Начальные условия системы уравнений (8) - (11) записываются в виде

p(0)=P₀; T^ = T_ti; T_w(o) = T_o; g,(o) = O.

Начальные и граничные условия для систем уравнений (13) - (16) записываются следующим

^Р р(М=Р₀; Т(О,х) = Т_о; G(0,x) = 0; ^(О,г) = Т_о; g,(0,x) = 0.

На входе в КС

Р^ = Рв (^т) + р(^т)^² (^т’°)

[л-1 ^{в вХ} ’ к-1 р(т) 2 5пИ = 0;

На границе КС и КО задаются условия перехода в виде

Gkc(t,Lkc) = Gko(t,0);

^Акс (^т- ^LKC) = ко (^Т’О);   / [G, р_кс (т, L_KC ), р_к0 (т,0)] =0;

Кп^к,^ 8п,ко№» gA^^^g^M', 8x^ = 0

На выходе из КО граничное условие задаётся в виде

G(t,LK0) = -

Ц50. ——РкоРко

V к -1

Рн

V Рко у

vi/k , х^к"

Рн

<РкО у

p.S0

2 Г2к

к +1

7 , . Рко Рко ¹ к + 1

Рн

Рко

хк/(кЧ)

Рн J ²

’ Рко U + 1J

2 V/Ы)

k +1J

Обыкновенные дифференциальные уравнения решаются методом Рунге-Кутта 4-го порядка. Уравнения (13) аппроксимируются неявной разностной схемой и приводятся к двухточечному разностному уравнению [5]

AnYn-Bn4Yn

где А,В- матрицы 3x3 , С - вектор размерности 3; У' = |G,7\p|; п - номер узла сетки по х.

Граничные условия (19) преобразуются к виду [5]

А^"^^(25)

где Aj - матрица 2x3, C_s - вектор размерности 2.

Первые три условия перехода (22) приводятся к виду [5]

Сс=«С+Х*’(26)

где а* - матрица размерности 3x3, %* - вектор размерности 3.

Граничное условие (23) записывается в виде [5]

BnYTX=Cn,(27)

где B_N -матрица 1x3, C_N - скаляр.

Краевая задача (24) - (27) решается методом ортогональной прогонки [5].

По рассмотренным математическим моделям были выполнены расчёты модельного НТГГ с карбонатом аммония в качестве охладителя. Охладитель применялся в виде гранул с гладкой поверхностью типа Ш (шар), СЦ (сплошной цилиндр, диаметр равен длине), ПЦ (полый цилиндр) и в виде сплошного цилиндра, прессованного из порошка (ПСЦ) [6]. Количество охладителя рассчитано из условия охлаждения продуктов сгорания топлива до 400 К. Размеры гранул всех типов одинаковы и равны 6 мм.

Рис. 2. Изменение температуры в КО с гранулами разного типа

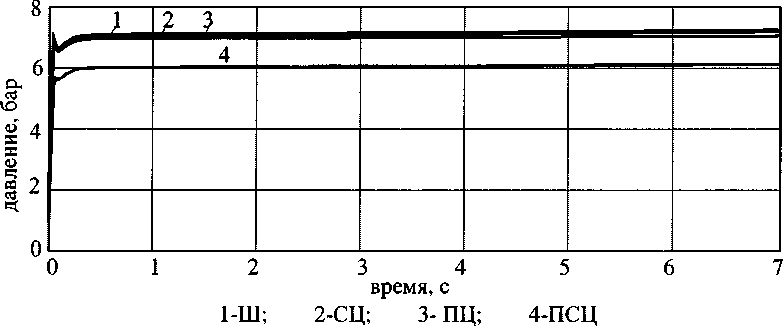
Рис. 3. Изменение давления в КО с гранулами разного типа

На рис. 2, 3 представлены результаты расчёта модельного НТГГ по термодинамической модели. Как следует из рис. 2, наилучшие результаты получены для гранулы типа ПСЦ, однако и в этом случае не удалось получить заданную температуру. Время работы НТГГ определяется временем горения заряда топлива.

На рис. 3 показано изменение давления в КО. Уровень температуры в КО связан с площадью поверхности разложения, и чем больше поверхность, тем ниже уровень температуры вследствие увеличения массы разложившегося охладителя.

Расчет и конструирование

Наиболее простой из одномерных моделей является модель с неподвижными гранулами. Предполагается, что в процессе работы НТГГ гранулы охладителя неподвижны. В результате разложения меняется пористость слоя охладителя.

На рис. 4, 5 показано изменение температуры и давления на выходе из КО с гранулами различного типа. Как следует из расчётов, тип гранулы оказывает существенное влияние на изменение температуры на выходе из КО и почти не влияет на характер изменения давления. Уровень температуры на выходе из КО намного меньше, чем в термодинамической модели. Уровень давления намного выше, чем в случае термодинамической модели. В термодинамической модели не учитывается гидравлическое сопротивление слоя гранул, поэтому уровень давления как в КО, так и в КС заметно ниже, чем в одномерной модели. В результате время горения топлива по термодинамической модели на 40 % больше. Уровень температур на выходе из КО заметно ниже, чем в термодинамической модели.

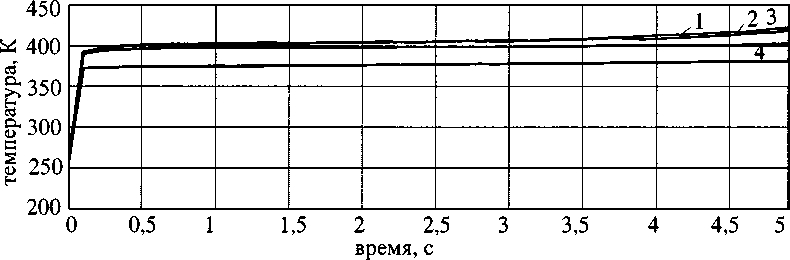
1-Ш; 2-СЦ; 3-ПЦ; 4-ПСЦ

Рис. 4. Изменение температуры на выходе из КО с гранулами разного типа

		1 2	3 4

0	0,5	1	1,5	2      2,5	3     3,5	4	4,5	5
				время, с
			1-Ш;	2-СЦ; 3-ПЦ;	4-ПСЦ

Рис. 5. Изменение давления на выходе из КО с гранулами разного типа

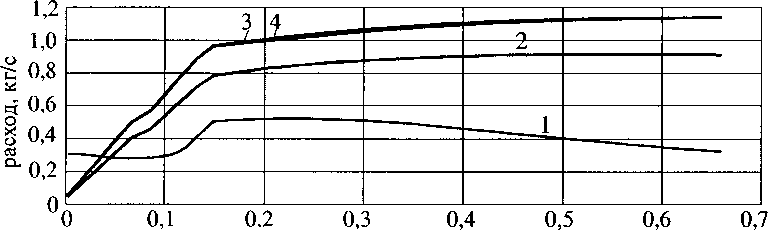
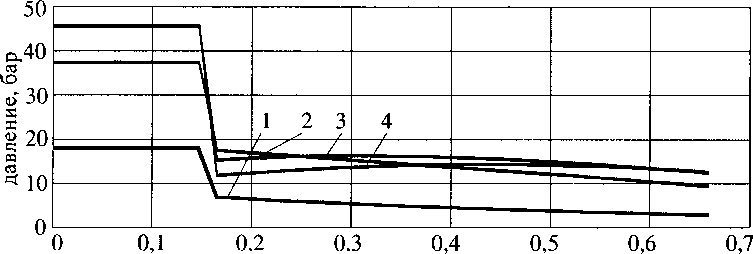
На рис. 6-8 показано изменение температуры, расхода и давления по длине НТГГ в различные моменты времени. Момент времени 0,02 с соответствует периоду горения воспламенителя. В процессе разложения гранул в рамках принятой модели их размеры уменьшаются, что приводит к увеличению пористости и уменьшению гидравлического сопротивления. Кроме того, при разложении гранул в поток поступает масса газа. Всё вместе взятое приводит к увеличению давления в первой половине длины КО.

В процессе работы гранулы под действием потока газа смещаются в направлении течения. Данное обстоятельство было учтено в одномерной модели. Принято, что при разложении гранул они перемещаются в направлении течения таким образом, что пористость слоя остаётся постоянной. Таким образом, в КО появляются область, свободная от гранул и область, занятая гранулами. Результаты расчёта по данной модели представлены на рис. 9-13.

На рис. 9-11 представлено изменение температуры, расхода и давления по длине КО с гранулами типа ПСЦ в различные моменты времени.

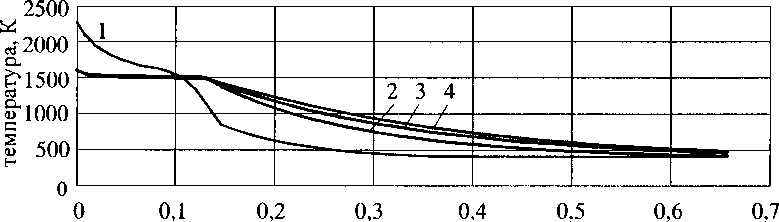
длина, м

1-т=0,02с;   2-т=0,2с;   3-т=2,0с;   4-т=4,0с

Рис. 6. Изменение температуры по длине НТГГ

длина, м

1-т=0,02с;   2-т=0,2с;   3-т=2,0с;   4-т=4,0с

Рис. 7. Изменение расхода по длине НТГГ

длина, м

1-т=0,02с;   2-т=0,2с;   3-т=2,0с;   4-т=4,0с

Рис. 8. Изменение давления по длине НТГГ

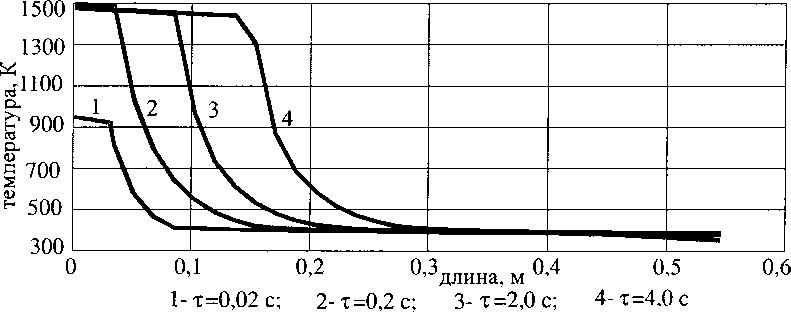
Рис. 9. Изменение температуры по длине КО

Расчет и конструирование

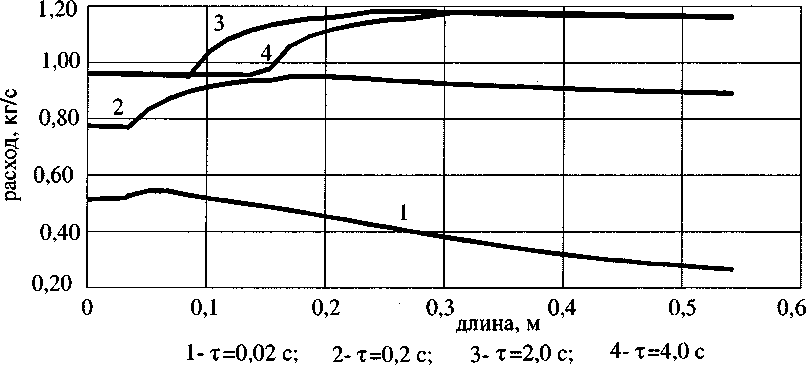
Рис. 10. Изменение расхода по длине КО

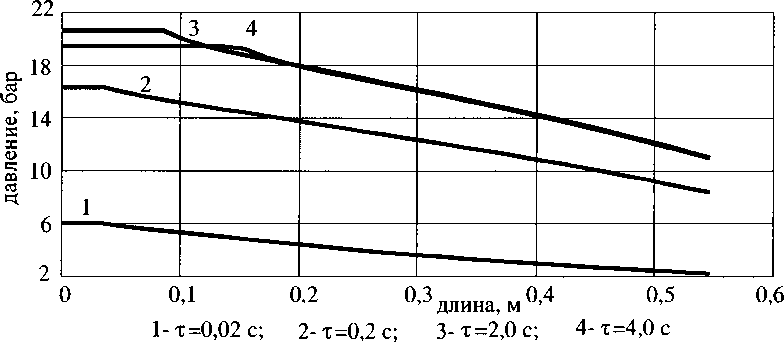
Рис. 11. Изменение давления по длине КО

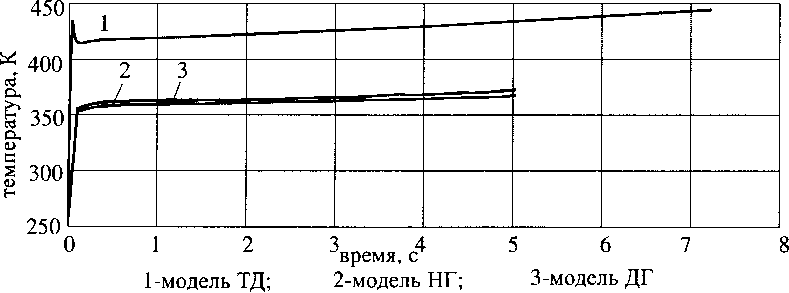
Рис. 12. Температура на выходе из КО

На рис. 12, 13 представлены изменение температуры и давления в КО с гранулами типа ПСЦ, полученных по термодинамической модели (модель ТД), одномерной модели с неподвижными гранулами (модель НГ) и одномерной модели с движущимися гранулами (модель ДГ).

Как следует из рис. 12, 13, значения температуры и давления на выходе из КО и характер их изменения во времени, полученных по одномерным моделям, мало отличаются друг от друга, хотя характер изменения параметров КО по длине в моделях НГ и ДГ различаются заметно.

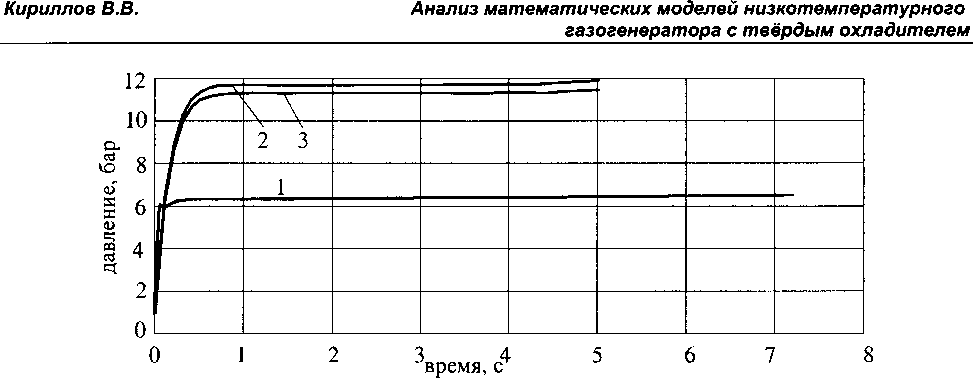
1-модель ТД; 2-модель НГ; 3-модель ДГ

Рис. 13. Давление на выходе из КО

Заключение. Термодинамическая математическая модель не позволяет получить требуемый уровень температуры в КО НТГГ и не учитывает гидравлическое сопротивление слоя гранул. Это приводит к занижению давления в КС и завышению времени горения топлива. Одномерные математические модели КО позволяют учесть особенности протекания процессов гидродинамики и тепломассообмена.