Анализ математической модели кольцевой роторной печи
Автор: Минкина Татьяна Владимировна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 1 (44) т.10, 2010 года.
Бесплатный доступ
Описана дискретная модель температурных полей кольцевой роторной печи. Составлена компьютерная программа для расчёта тепловых процессов и построена передаточная матрица рассматриваемого объекта. С помощью спектров Гершгорина исследованы характеристики передаточной матрицы тепловых полей рассматриваемой печи как объекта управления.
Дискретная модель, передаточная матрица, диагональная доминантность
Короткий адрес: https://sciup.org/14249325
IDR: 14249325 | УДК: 681.536
Текст научной статьи Анализ математической модели кольцевой роторной печи
Кольцевая роторная печь (рис.1), как показывают расчёты, является более энергосберегающей по сравнению с традиционными печами, применяемыми для производства 1 т извести. Основная задача технологического процесса заключается в термической обработке исходного материала (щебня), перемещаемого вдоль печи специальным устройством.
Рис.1. Схема объекта управления: 1 – вход и выход камеры; 2 – форсунки; 3 – датчики, измеряющие температуру в камере; 4 – кирпичная кладка; 5 – теплоизоляционная обмазка; D – диаметр наружной стенки кирпичной кладки; Θ 1 , X 1 , X 2 , X 3 , Y 1 , Y 2 , Y 3 – геометрические размеры печи
Температурное поле в печи должно соответствовать технологическим условиям обработки щебня. В связи с этим задача проектирования системы управления температурным полем печи приобретает особую важность.
Постановка задачи . Для проектирования системы управления температурным полем кольцевой роторной печи необходимо решить следующие задачи:
-
- описать математическую модель температурных полей кольцевой роторной печи;
-
- построить передаточную матрицу объекта управления, связывающую вектор входных воздействий (тепловые потоки форсунок) и вектор функций выхода (температуру в точках установки датчиков);
-
- рассмотреть возможные методы синтеза системы управления температурным полем рассматриваемого объекта;
-
- синтезировать систему управления.
Рассмотрим решение первых трех задач.
При разработке дискретной модели температурных полей кольцевой роторной печи сделаем следующие допущения:
-
- будем полагать, что температура на входе и выходе камеры 1 поддерживается постоянной; датчики измерения температуры 3 расположены внутри печи в точках X 1 -X 3 , Y=Y 2 , Θ дi ( i= 1,…, 5);
-
- нижняя часть нагревательной камеры и боковые поверхности теплоизолированы; щебень рассыпан равномерно по дну печи;
-
- скорость движения щебня в нагревательной камере 0,0222 м/мин;
-
- управляющим (входным) воздействием служит тепловой поток, вырабатываемый путём сжигания природного газа в форсунках 2, а его плотность вычисляется по формуле Q i =P i /X 3 Y 4 , P i – мощность, выделяемая i- й форсункой.
Геометрические параметры рассматриваемой печи: D= 9,88 м; X 1 = 1,40 м ; X 2 = 0,20 м; X 3 = 0,20 м; X 4 = 0,30 м; Y 2 = 0,4 м; Y 3 = 0,15 м; Y 4 = 0,8 м; Θ 1 =300 .
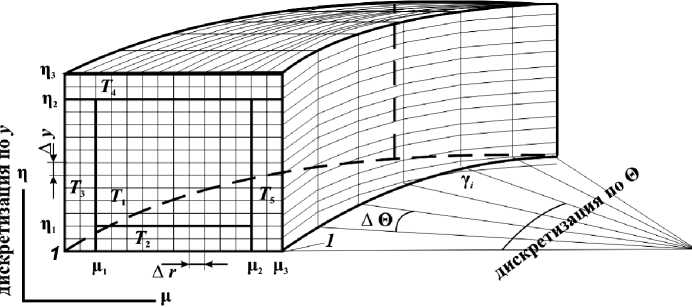
Дискретная модель. Схема дискретизации математической модели [1] рассматриваемого объекта управления приведена на рис. 2. В рассматриваемой задаче будем полагать, что по выбранной координате шаг дискретизации остается постоянным.
дискретизация по г
Рис. 2. Схема дискретизации математической модели объекта управления:
T 1 –T 5 – температурные поля различных сред; μ – точки дискретизации по радиусу ( D/ 2) (μ=1,…, μ 3 );
∆r – шаг дискретизации по радиусу r ; η – точки дискретизации по координате y (η=1,…, η 3 );
∆y – шаг дискретизации по y ; γ – точки дискретизации по Θ (γ=1,…, γ k ); ∆Θ – шаг дискретизации по Θ
Согласно приведённой схеме дискретизации, математическая модель объекта управления в дискретном виде записывается следующим соотношением [1]:
Дт а ( i *- 1, n,Y i ,™ + 1^ +1 .n.Y
Л Ar2
1 Т . -Т
AT i MY
+ i ^Чпу i .wi.y +
D/2-Лтц ArТ , -ТГ +7: , 1 Г ,-2Т +г
i ,№1,Y i ,№Y i ,W1,Y + i ,№Y - 1 i ,№Y i ,ЦЛ,У + 1 -
Ay2 D/2-Ari A02
где At - шаг дискретизации по времени; a i - коэффициент температуропроводности i-й среды,
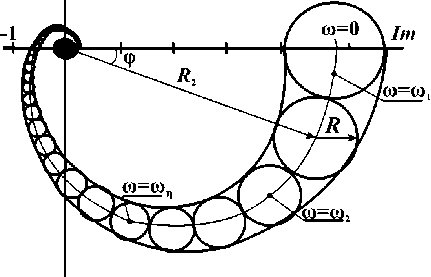
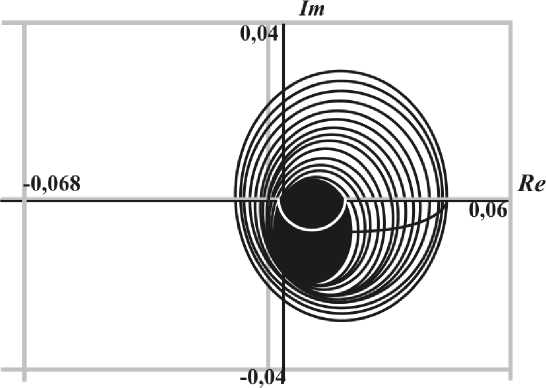
X ai = —; с - теплоемкость; X i - коэффициент теплопроводности; y — плотность, 1 Рис. 3. Схема дискретизации функций выхода Дискретные аналоги граничных условий [2] отражают неразрывность температур и температурных полей на границах раздела сред. Для фазовой переменной Т1 они могут быть записаны в виде следующих соотношений X1 г -т . 1,^1,1,Y 1,^1+1,1,Y Δr — X3 3,Ц1-l,n,Y l,^i,1,Y . ; η1<η<η2, 1<γ<γk; X1 1,^2,1,Y ^“ Г . 1,Ц2 +1,1,Y Δr — Х5 1,^2,n,Y 52Ц2+1>1^. ; η1<η<η2, 1<γ<γk; Г -Т ., -Т ^ntT 1,M2-1,Y _ л 4,Ц,П2+1,Y ' 1 л = Х4л Δy Δy μ1<μ<μ2, 1<γ<γk; 1,Ц,П1 +1,Y 1,кП1,У _; 1,Н,П1,Г 2,Ц,П1 -1,Y . '1 — ^9 ; Δy Δy μ1<μ<μ2, 1<γ<γk, где λ1– коэффициент теплопроводности первой среды. Аналогичными соотношениями записываются граничные условия и для других фазовых переменных: T^i— 0; T^п — о; м=1мз,n=iпз. ,μ,η, ,μ,η,γk Дискретный аналог входного воздействия Qi, (i=1,…, 5) на объект управления (см.рис.3) записывается в виде следующих соотношений: - Т λ 1,μ1,η, γ - 1,Ц1 + 1,ПЛ A r — Qj, η1<η<η2, γj<γ<γj+1; j=1,…, 5, где Qj – тепловой поток, выделяемый j-й форсункой (j=1,…, 5). Функцией выхода служат значения температурного поля в точках установки датчиков Тi,μdi, ηdi, γdi (μdi,ηdi,γdi (i=1,…, 5) – координаты точек установки датчиков) (рис.3), Qj – количество теплоты, выделяемое j-й форсункой (j=1,…, 5). При моделировании объекта были использованы следующие значения геометрических и физических параметров: D=9,7; X1=1,42; X2=0,22; X3=0,4; Y1=0,8; Y2=0,4; Y3=0,12; Y4=0,8; μ1=3; μ2=15; μ3=17; η1=3; η2=14; η3=18; ∆r=0,1; ∆y=0,06; Θ=2,50;γk=120; γ1=23, γ2=25, γ3=41, γ 4=43, γ5=59, γ6=61, γ7=77, γ 8=79, γ9=95, γ10=97; di=14, ηdi=8, (i=1,…,5); γd1=8, γd2=26, γd3=44, γd4=62, γd5=90. Q=1000W a1=0,014 – воздух; a2=0,016 – кирпич; a3=0,008 – щебень; ld1=18 – воздух; ld2=23 – кирпич; ld3=20 – щебень; V=0,00037 – м/с. По результатам расчетов получена передаточная матрица W рассматриваемого объекта, связывающая вектор входных воздействий (тепловые потоки форсунок) и вектор функций выхода (температуру в точках установки датчиков): 0,015e-70S 2060S+1 0,051e-ios 2380S+1 0,042e-bos 5140S+1 0,0315 -380S e 7440S+1 0,016 -1100S e .8600S+1 0,0125 0,0095 0,0065 0,004 -1700S e 90S e 550S e 000S e 700S 5020S+1 6900S+1 840OS+1 860OS+1 0,050 0,0385 0,0265 0,0155 -Ю305 e 70S e 0S e 5 0S --------e 4460S+1 6920S+1 8520S+1 8940S+1 0,0765 -12s 0,068 s 0,0465 -250S 0,027 6. 4276S+1 5880S+1 770OS+1 820OS+1 0,059 e-13os 0,083 e-8s 0,067 e-50S 0,039 e-250S 6740S+1 4984S+1 570OS+1 680OS+1 0,030 e-560S 0,042 e-240S 0,0555 e_50s 0,056 e-7s 8480S+1 6920S+1 470OS+1 e 2486S+1 Выделим два сложившихся в настоящее время подхода для построения замкнутых систем управления рассматриваемым объектом, передаточная матрица которого приведена выше: решение методами сосредоточенных систем и решение методами систем с распределёнными парамет- рами. Решение методами сосредоточенных систем основывается на свойстве диагональной до- минантности передаточных матриц объекта управления [2,3]. Положим, что в результате экспе- Re Рис.4. Построение спектра Гершгорина: ωη – заданные значения круговой частоты ω; φ=arctg(Im(Wi,i(jω)/Re(Wi,i(jω)), R2=[(Im(Wi,i(jω))2+Re(Wi,i(jω))2]1/2; m R= £ [(Im(W,j))2 +RW)№ j=1, j * i i, j=1, 2,..., m, mx m - размерность матрицы W риментальных исследований получена передаточная матрица, связывающая j-й вход с i-м выходом: W(5) = ^,7- (^)]. Исследуем полученную передаточную матрицу. Полагая s=jω, где ω – круговая частота, определим модули и фазы элементов матрицы W. Если модули диагональных элементов матрицы W намного больше суммы модулей остальных элементов соответствующей строки, то матрица W обладает свойством диагональной доминантности [3]. Исследование диагональной доминантности может быть осуществлено с помощью спектров Гершго-рина для заданной передаточной матрицы. При этом для каждого значения ω= ωη могут быть построены круги Гершгорина, объединяя которые, получим спектр Гершгорина (спектр Гершгорина, построенный для i-й строки диагонально-доминантной матрицы, приведен на рис. 4). Для диагонально-доминантных матриц разработана частотная методика синтеза многомерных систем управления [3]. В рассматриваемой задаче диагональная доминантность отражает взаимовлияние j-го входного воздействия на i-й выход. На рис.5 показан спектр Гершгорина для первой строки передаточной матрицы рассматриваемого объекта (W). Аналогично могут быть построены спектры Гершгорина и для остальных строк матрицы. Рис. 5. Спектр Гершгорина для первой строки матрицы W Выводы. В рассматриваемой статье описана дискретная модель температурных полей кольцевой роторной печи и построена передаточная матрица рассматриваемого объекта. С помощью спектров Гершгорина исследованы характеристики передаточной матрицы. Результаты расчётов показали, что передаточная матрица рассматриваемого объекта не обладает свойством диагональной доминантности, т.е. взаимосвязи между j-м входным воздействием и i-й функцией выхода достаточно существенны, и их нельзя не учитывать. Следовательно, методика синтеза регуляторов многомерных систем управления, опирающаяся на диагональную доминантность передаточной матрицы объекта управления, не может быть использована. В рассматриваемом случае может быть использована методика синтеза систем с распределёнными параметрами, описанная в [4].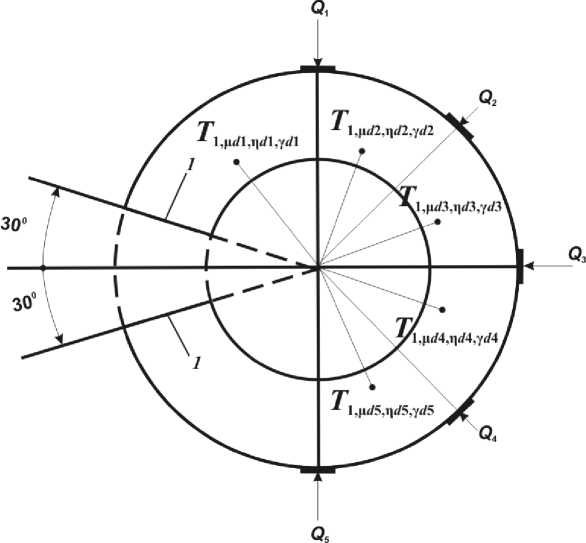
Список литературы Анализ математической модели кольцевой роторной печи
- Минкина Т.В. Математическая модель кольцевой роторной печи/Т.В. Минкина//Управление и информационные технологии: межвуз. науч. сб. -Пятигорск, 2008. -С.121-128.
- Воронов А.А. Основы теории автоматического управления/А.А. Воронов//Автоматическое регулирование непрерывных линейных систем. -М.: Энергия, 1980. -309 с.
- Солодовников В.В. Частотный метод анализа и синтеза многомерных систем автоматического управления: учеб. пособие/В.В. Солодовников, Н.А. Чулин. -М.: Высшая школа, 1981. -46 с.
- Малков А.В. Синтез распределенных регуляторов для систем управления гидролитосферными процессами/А.В. Малков, И.М. Першин.-М.: Научный мир, 2007. -252 с.


