Анализ математической модели теплосъема с плоской поверхности ламинарно движущимся хладагентом через сопряженную пористую среду

Появление компактных энергонапряженных элементов систем различного предметного назначения вызвало необходимость их эффективного охлаждения с целью стабилизации температурного режима, обеспечивающего заданные эксплуатационные характеристики [1]. Решение этой проблемы базируется на использовании различных методов интенсификации теплообмена. [2], но наибольшее применение нашли пористые среды [3] в силу высоких значений коэффициента теплопередачи.

Физическая модель пористых сред, как правило, представляется в виде плотной упаковки сфер [4], пустоты которой соединены между собой и заполнены жидкостью, причем присутствуют только две фазы - жидкость и пористый недеформируемый скелет.

Гидродинамика, пористого слоя описывается обобщенной феноменологической моделью Дарси - Бринкмана - Форчхеймера в форме Key - Ченга [5]:

• V- V = 0;                                (1)

Pf dv   ( V •v ) V]     _                  Г V     bV I V I

• -    ⁺     = Plg^{-Vp + p}f^{VV -} ^ K + p , -^ ;      (2)

где t - время: p,. p, - плотность ii дниамичесжая вязкость жидкости: е - доля свободного объема (пористость); V - вектор скорости жидкости; g - вектор ускорения свободного падения; p - давление. Проницаемость пористой среды определяется из модифицированного соотношения Козени - Кармана [6].

K = е ² dp/ [150(1 - е )] ,                                (3)

фактор трения Форчхеймера равен b ^ 0,0117dp/ (1 - е),

где dp - среднечисленный диаметр сферических частиц в пористом слое.

Уравнение энергии обычно записывается для каждой фазы (двухтемпературная модель) в форме Шуманна [7]:

для жидкости е (Pcp)f ^ + е (Pcp)f V •Vtf = V • (Af • Vtf) ± asf asf (ts - tf);          (5)

для скелета

∂t

^{(1 - E} ) ^{( p}cP ) s дТ = ^V • ⁽ ^e • ^Vts ) У ^asf asf ⁽ ts ^- tf ) ,                  (6)

где Af, Ae - тензоры эффективных коэффициентов теплопроводности жидкости и скелета; tf, t_s- температуры жидкости и скелета; asf - коэффициент теплоотдачи между жидкой фазой и матрицей пористого скелета; asf - удельная площадь смоченной поверхности в пористом теле; p_s, c_ps - плотность и удельная массовая теплоемкость скелета пористого тела; cpf - удельная массовая теплоемкость жидкости.

Уравнения (1), (2), (5) и (6) получены методом объемного осреднения [4].

Если теплофизические параметры в (5) и (6) однородны по пространственным координатам и не зависят от температуры, то их, как показано в [8], можно вычислить из соотношений:

asf = b ^{(1 — е} ) ^/dp ;                                    (~)

asf = Af [2 + 1 , 1Pr * ¹ / ³ ( pf I V I dp/^f )⁰ ’ 6] /dp,                      (8)

где Pr * = ^fcpf/Af; Af - теплопроводность жидкости;

Af = [ е + (0 , 1 : 0 , 5) Pr ( ffp] ^ Af ;

As = (1 - е ) As, (10) где As - теплопроводность скелета пористого тела.

Учитывая феноменологический характер модели в пористом слое постановка граничных условий осуществляется в рамках классического анализа задач теплопереноса для гомогенных сред [9].

Плоская геометрия охлаждаемых тепловыделяющих элементов конструктивно обуславливает такую же геометрию пористых теплообменников, поэтому большинство исследований сосредоточилось на анализе плоских теплообменников с тепловыми граничными условиями первого и второго рода со стороны охлаждаемой поверхности [10]. Даже в такой простой геометрической постановке интегрирование системы (1), (2) и (5), (6) вызывает такие же затруднения, как и при совместном интегрировании уравнений Навье - Стокса и теплопереноса [11]. Подробный обзор численных и приближенных аналитических способов решения системы (1), (2) и (5), (6) при различных граничных условиях для плоской геометрии приведен в [12], где анализируется эффективность спектра конечно-разностных и конечно-элементных методов, а также новая технология получения приближенных решений в аналитическом виде - гомотопно-пертурбационный метод.

Однако во всех конкретных формулировках объявленной задачи гидродинамическим начальным участком пренебрегают на основании метода анализа размерностей без указания конкретных зависимостей, связывающих геометрические, гидродинамические и теплофизические характеристики пористой среды [13]. Отсутствие таких данных приводит к выбору заведомо завышенных значений длины начального гидродинамического участка, например в [14]. Поэтому в данной работе такая зависимость идентифицируется в широком диапазоне основных параметров при ламинарном течении теплоносителя в рамках Бринкмановского приближения модели Дарси - Бринкмана - Форчхеймера и находятся условия, при которых влиянием длины гидродинамического начального участка на теплопередачу можно пренебречь.

1.    Математическая модель

Характерной особенностью при оформлении конструкции плоского пористого теплообменника является существенное превышение ширины над высотой его поперечного сечения, что позволяет рассматривать проточную область как плоский канал в 2D декартовой системе координат (рис. 1).

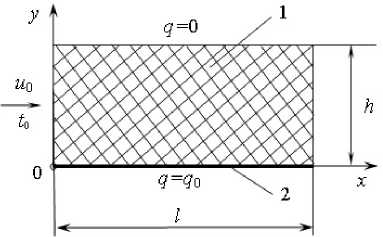
Рис. 1. Расчетная схема: 1 - пористое тело; 2 - тепловыделяющий элемент

Пусть однородный по сечению поток теплоносителя с температурой t 0 и со скоростью и 0 подается на вход теплообменника высотой h и длиной 1. Полагаем стенки теплообменника непроницаемыми для теплоносителя, причем верхняя - теплоизолирована, а на нижней задан тепловой поток q0. Согласно принятой расчетной схеме уравнения (1), (2) и (5), (6) в безразмерной форме записи имеют вид:

	∂U ∂V dX + dY = ’	(и)
dp , i ( d 2 u ' dX + Re dX 2	∂U     ∂U     ∂U d6 + ф dX + V dY = + dY^  (Re)Da U + JD, U VU 2 + V 2) ;	(12)
dP I i ( d 2 v dY + Re dX 2	∂V     ∂V     ∂V 86 + U dX, + V dY = + dVY)        V + J D-a V VU 2 + V 2) ;	(13)

1 dTf + UdTf + VdTf _  1   / е d6 dX dY Рг • Re

∂ ² Tf ∂X ²

∂ ² Tf

⁺ dY ^{2 +}

∂Ts   ∂ ² Ts ∂ ² Ts

⁽¹ — ^e ) Asf ■ ^Рг • Re -— ^_ „ ₂ + „ ₂

∂θ   ∂X ²    ∂Y ²

-

Nu p •

<^Л Ts—Tf ); (Re p У^(л Ts^—Tf ) ,

где 6 _ u 0 т/ ( eh ): X _ x/h Y _ y/h U _ u/u 0: V _ v/u 0: u. v - компоненты вектора скорости жидкости V; P _ е ² p/ ( pfu 0); B _ e ² b Tf _ A^f ( tf — 1 0) / ( q 0 h ); Ts _ A; ( ts — 1 0) / ( q 0 h ); Л _ A^f/X^ Re _ pfu 0 h/ ( pfe ²) - число Рейнольдса; Re _p _ Pf u 0 dp/ [6 (1 — e ) pf ] - локальное число Рейнольдса: Da _ K/h ² - число Дарси: Рг _ е ( pcp ) f pf / XfPPf) ^ число Прандтля; Nu _p _ asf dp/Ae - локальное число Нуссельта;

Asf ^_

A^f ! ( pcp ) f ! [ A^f / ( pcp ) s ] - критерий, характеризующий диффузию теплоты

в жидкости относительно диффузии теплоты в скелете пористой среды.

Ламинарное течение теплоносителя позволяет принять гипотезу однонаправленности ( V = 0 , dP / dY _ const), а также пренебречь инерционными эффектами при

падении давления в пористом слое, что экспериментально подтверждено в [15]. При менение погранслойной линеаризации [16] с учетом связи 6 _ X / е сводит гидроди-

-

-

намическую подзадачу (11) - (13) к начально-краевой задаче для параболического уравнения

∂U ∂X с граничными условиями

-

1 dP 1 d ² U edX ⁺ e Re dY 2

-

U еRe • Da

U (0 , Y' ) = 1; U ( X, 0) = U ( X, 1) = 0 ,

где dP / dX определяется из сохранения расхода жидкости через поперечное сечение пористого канала

I U ( X,Y ) dY _ 1 .

Из (16) - (18) следует упрощение теплообменной подзадачи (14), (15) с учетом того, что диффузия теплоты в поперечном направлении пористого слоя существенно больше, чем в продольном ( d ² Tfs / dY ² ^ d ² Tf s / dX ²) [17]:

∂Tf

U ∂X

1    d ² T_f

Рг • Re dY ²

Nu_B • Re _z

+ ргй< (л Ts—Tf);

∂ ² Tf ∂Y ²

^_Nu -• (RI)² • ^(л Ts^- Tf ) ,

с тепловыми граничными условиями, отвечающими постановке задачи

Tf (0 ,Y ) _ 0;

dTf ( X, 0) _ dTs ( X, 0)

∂Y

∂Y

— 1;

dTf ( X, 1) _ dTs ( X, 1)

∂Y

∂Y

_ 0 .

Заметим, что полученная модель (16) - (23) может быть проанализирована последовательно, т.е. сначала гидродинамическая подзадача, а затем тепловая.

2.    Гидродинамическая подзадача

Линейность системы (16), (17) позволяет использовать одностороннее преобразование Лапласа [18] по переменной X и получить аналитическое выражение для безразмерной скорости

U ( X,Y ) = Ce Re • Da^1 - {sh ( y Da ^{- 1} / 2) + sh [(1 - Y ) Da ^{- 1} / 2] } / shDa ^{- 1} / 2^ +

+2

∞

Y n =1

Cε Re

Da + µ ² _n

-

1) ^{

sin ( MnY ) + sin [ Mn (1 - Y )] } x

x exp

(

Da + µ ² _n — ε Re

X    ( µn

cos µ_n

- sin Mn ) ,

где C = найдем

—e ¹ dP / dX, Mn = nn. Из (18) при X > x (полностью развитое течение)

C = e Re • Da

2 (chDa - ^1/2 - 1)

_Da - 1/2_shDa - 1/2

- 1

откуда коэффициент гидравлического сопротивления по Фаннингу [19] есть

£ = 4 e 2Re • Da

2 (chDa ^{- 1/2} - 1)

_Da - 1/2_shDa - 1/2

- 1

Отметим, что при отсутствии пористого скелета ( e ^ 1 , Da ^ х ) коэффициент сопротивления совпадает со значением при ламинарном течении ньютоновской жидкости в плоском канале [20].

Длина начального гидродинамического участка определена из условия

U ( х, 1/2) - U ( X, 1/2)

= 0 , 03 ,

U ( х, 1/2)

ограничиваясь первым членом ряда в (24)

X =

ε Re

Da ^{- 1} + π ²

ln

2sh(Da ^{- 1/2}/2)

5 • 10 3 CeRe • Da 1 - shDa-1/2

Cε Re

Da ^{- 1}+ π ^{2    1}

откуда, с учетом (25) следует, что длина начального участка при течении в пористой среде пропорциональна числу Рейнольдса и ширине плоского канала, а в пределе, когда, e ^ 1 , Da ^ х . получается класспческий результат X = 0 , 18Re [21].

Как и следовало ожидать, снижение числа Re при Da = const и e = const нивелирует влияние условий входа, на поле скоростей (рис. 2), также как и уменьшение числа, Da при Re = const ii e = const (pnc. 3).

В практически важном диапазоне пористости e = 0 , 1 ^ 0 , 5 заметного изменения структуры поля скорости при различных Re и Da не наблюдается. Однако влияние

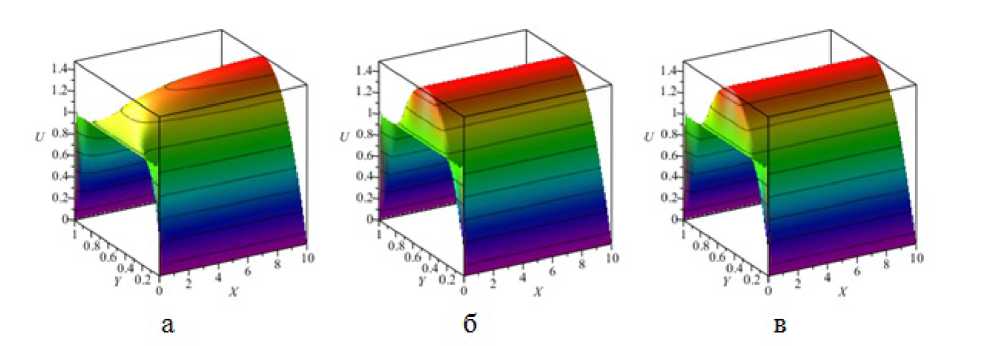
Рис. 2. Поле скоростей в плоском пористом канале при е =0 ,4; Da=l и различных числах Re: а, - 100: б - 1: в - 0.01

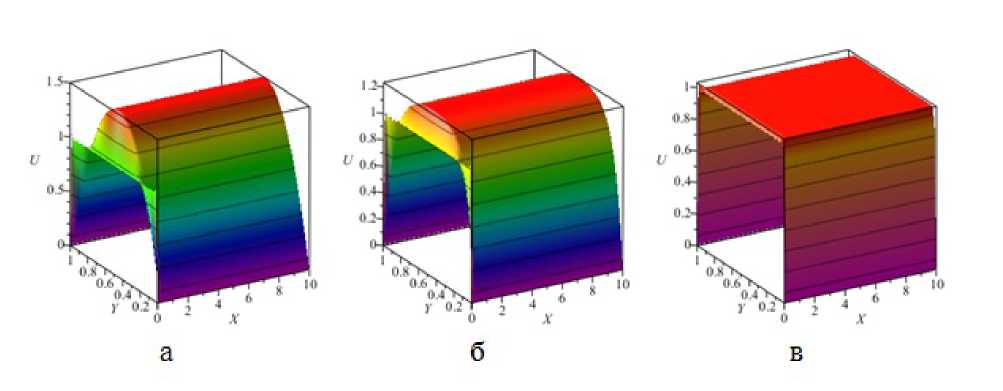
Рис. 3. Поле скоростей в плоском пористом канале числах Da: а, - 100: б - 0.01: в - 1 • 10 ~ ⁴

при Е = 0,4; Re = 1 и различных уменьшения пористости становится существенным на коэффициент гидравлического сопротивления, увеличивая его значение более чем на порядок (рис. 4) и уменьшая длину начального гидродинамического участка до характерного размера пор dp (рис. 5). На рис. 6 проиллюстрировано подтверждение количественной адекватности принятых допущений при синтезе математической модели гидродинамической подзадачи. Эффективность пористых теплообменников проявляется при разумном уменьшении величины проницаемости (Da ^ 0) в контексте потерь напора на преодоление сил гидродинамического сопротивления и увеличении площади поверхности теплопередачи между фазами. Но в этом случае профиль скорости течения жидкости в плоском слое по структуре соответствует режиму идеального вытеснения (рис. 3 в), что дает основание упросить тепловую подзадачу, считая в конвективном слагаемом уравнения (19) U ~ 1.

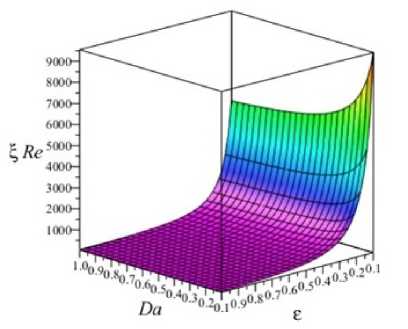
Рис. 4. Коэффициент гидравлического сопротивления, рассчитанный по формуле (26)

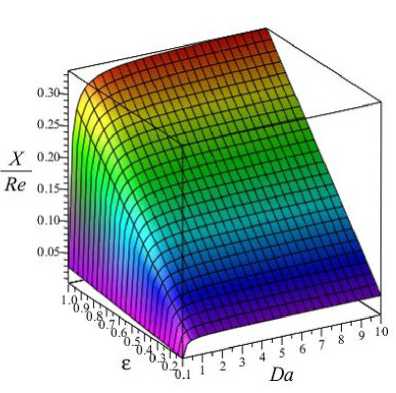
Рис. 5. Длина гидродинамического начального участка, рассчитанная по формуле (27)

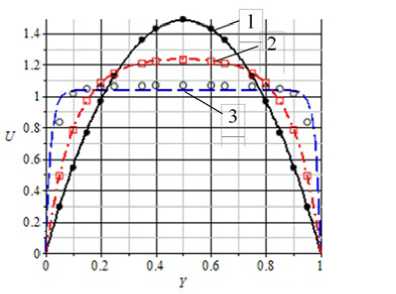
Рис. 6. Профили скоростей в плоском пористом слое при X = 20 и Re = 1 и различных Da: 1 - 0.3: 2 - 0.01: 3 - 0.00033 (- расчет: о данные из [17])

3.    Тепловая подзадача

Анализ гидродинамической подзадачи позволил получить аналитические выражения для Tf и Ts путем последовательного применения одностороннего преобразования Лапласа по переменной X и конечного косинус-преобразования Фурье по переменной ¥ [22]:

f ( , ) = Pr • Re Of

∞

f

[1 — exp ( -aX )] + 2 ^^ "k cos ( nkY ) [1

к =1

^— exp ( ^—bfX ) ]; (28)

Ts ( X,Y) = W~ • (1Г ) ²

N up   Re

1     2 X

Л + Pr • Re • Л ⁺

где

∞        cs

+2     dsk + b [1 - exp k=1          k

( -b^s_kX )] cos ( πkY ) ;

_f    N up · Re 1

Pr · Re p   Re p

-

1;

f ck =

2Nu p· Re        π 2 k 2

Pr · Re² p ^{Λ +} Pr · Re

2;

π ² k ² +N up · _R ^R _e ^e _p  Λ

b     π2k2 Nup · Re bk = Pr · Re + Pr ·Re2p

-

Nu² p Re³ Pr Re⁴ _p

^л Р² к ² + Nu p • (RR p ) л] ;

Re ² 2Nu · Re      π ² k ²                        Re ^{2 2}

c^sk =Nu p· _{Re p     Pr ·} ^p _Re2 _p Λ+_{Pr · Re}       π ² k ² + Nu p · _{Re p} Λ ;

d^s_k =                         ₂ .

π ² k ² +Nu p · R^Re^e _p Λ

Расчетный анализ тепловой подзадачи выполнен для теплоносителя с теплофизическими свойствами, близкими к воде: pf = 0 , 5 • 10 ~ ³ Пас; pf = 1000 кг/м³; Xf = 0 , 68 Вт/(м • К); cpf = 4190 Дж/(кыК). Пористый скелет - алюминий с теплопроводностью X_s = 211 Вт (м - К). Геометрические парад гетры таковы: /z=0.01 м: dp = 0 , 5 • 10 ~ ³ м. Скорость теплоносителя выбрана равной и 0 = 0 , 2 м/с. При таких исходных данных получены следующие результаты.

Уменьшение пористости приводит к более интенсивному охлаждению скелета (рис. 7), причем поле температур существенно неоднородно, т.е. вблизи « горячей » поверхности температура значительно выше температуры около теплоизолированной поверхности. Это объясняется тем, что скорость теплоносителя при меньшей пористости увеличивается в поровом пространстве и, следовательно, его температура уменьшается (рис. 8). Кроме того, наблюдается относительный локальный перегрев теплоносителя в пограничном слое на « горячей » стенке, что может вызвать при определенных условиях фазовый переход в теплоносителе. При значительной длине теплообменника этот перегрев принимает постоянную величину (рис. 9), что свидетельствует о наступлении теплового равновесия между теплоносителем и пористым скелетом.

Вычисленное локальное число Нуссельта (рис. 10)

Nu(X)= [Tf (X, 0) - Tf (X)]" 1, где

Tf ( X ) =   ¹

Tf ( X,Y ) dY,

показывает, что наиболее эффективно пористый теплообменник функционирует при относительной его длине <  100, т.е. на начальном тепловом участке, где значения безразмерного коэффициента теплоотдачи более чем на порядок выше по сравнению с аналогичным теплообменником без пористого скелета [23].

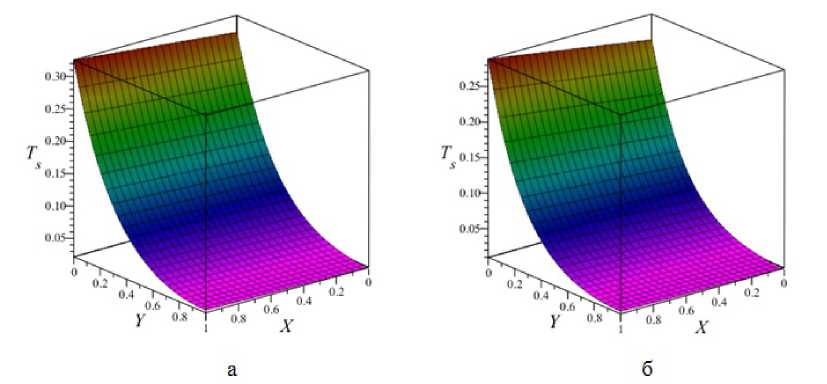
Рис. 7. Поле скоростей в плоском пористом канале при в=0,4; Da=l и различных числах Re: а, - 100: б - 1

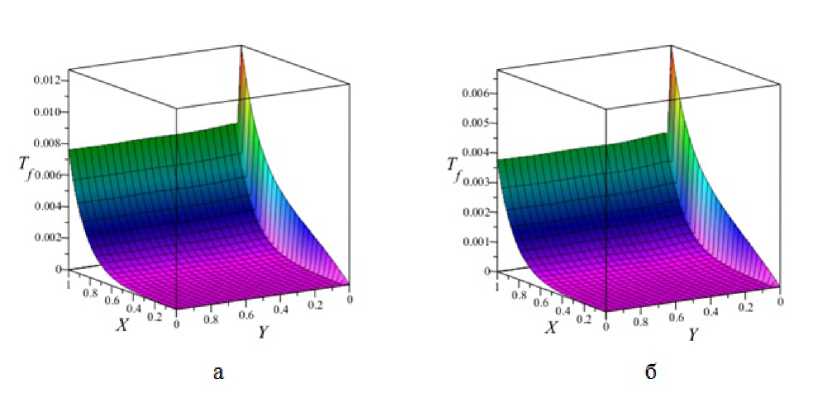
Рис. 8. Поле температур теплоносителя в пористом плоском теплообменнике: а - 6 = 0 , 7-.б - = = 0 , 5

Заключение

Предложенная математическая модель, отвечающая условиям адекватности и корректности, позволяет рассматривать ее как инструментарий при выборе рациональных параметров плоского пористого теплообменника с требуемыми теплофизическими характеристиками.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках Федеральной целевой программы (Соглашение № 14.577.21.0202, уникальный идентификатор RFMEFI57715X0202).

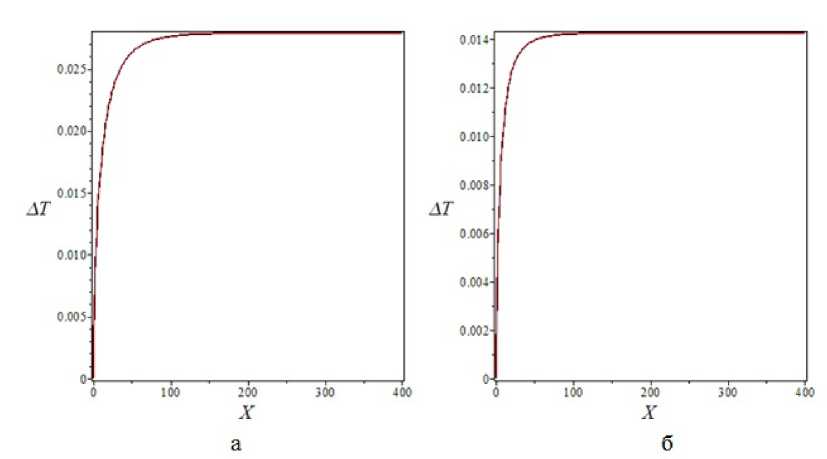
Рис. 9. Температура перегрева теплоносителя у « горячей » стенки относительно средней температуры по сечению теплообменника: а - е = 0 , 7; б - = = 0 , 5

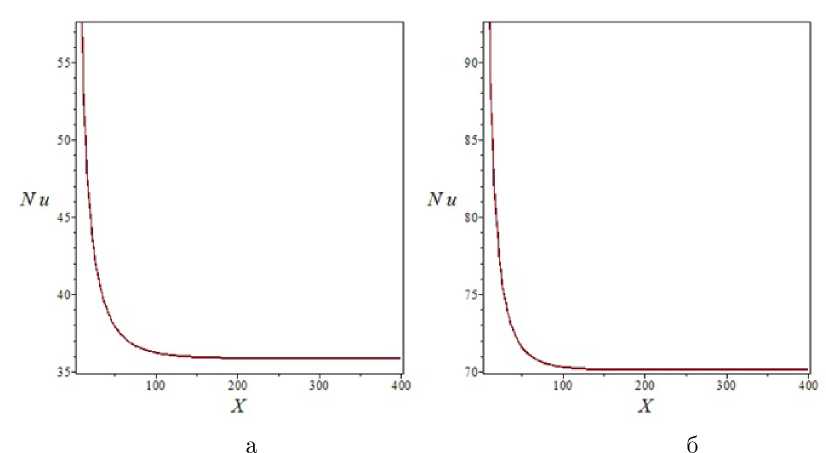
Рис. 10. Локальное число Нуссельта: а - е = 0 , 7; б - е = 0 , 5