Анализ методов эффективного выбора инвестиционных проектов для металлургического предприятия

DOI:

Цитирование. Подгорная Н. А., Мотченко Л. А., Чумаченко В. Н. Анализ методов эффективного выбора инвестиционных проектов для металлургического предприятия // Вестник Волгоградского государственного университета. Серия 3, Экономика. Экология. – 2018. – Т. 20, № 3. – С. 61–71. – DOI: 10.15688/jvolsu3.2018.3.7

Проблема и ее связь с научными и практическими задачами

Металлургическая промышленность играет существенную роль в мировой экономике, являясь основой строительной отрасли, а также оборонно-промышленного (ОПК) и топливно-энергетического комплексов (ТЭК). Доля металлургии в общем объеме промышленности России близка к 10 %, а износ основных фондов стремится к 50 % [12].

На конкурентоспособность предприятий данной отрасли влияет технический уровень основных фондов, что ставит перед металлургической промышленностью задачу модернизации, технического перевооружения и существенного инвестирования в производство.

Анализ сущности и задачи управления инвестициями предприятия отражены в трудах отечественных ученых: В.В. Андреева, В.В. Бочанова, Н.В. Игошина, А.В. Идрисова, Т.Г. Касьяненко, В.П. Красовского, В.М. Лебедева, В.Н. Лившица, B.Д. Миловидова, Н.Л. Ма-ренкова, С.А. Смоляка, М.А. Субботина и др., а также зарубежных ученых: И. Ансоффа, Г. Бирмана, Ю. Бригхэма, Дж. Кейнса, Р. Оуэна, Б. Санто, Б. Твисса, С. Шмидта и др. Инвестиционным процессам в металлургии посвящены работы В.В. Андреева, Л.В. Дорохова, В.Б. Прутковского, В.М. Сафонова, А.Б. Серплина, А.Н. Смирнова, А.Ю. Цупрун.

Экономико-математические модели оптимального выбора рассмотрены в работах И.А. Бланка, В.А. Вербы, П.Л. Виленского,

В.А. Диленко, В.В. Ковалева, Н.Н. Лепа, Н.Л. Маренкова, В.В. Мыльника.

Несмотря на наличие большого ряда исследований по рассматриваемой теме, не исключается необходимость дальнейшего развития теоретических и методических положений, а также обобщения практического опыта, имеющегося в данной области. Однако анализ работ, опубликованных по теме исследования, свидетельствует, что остаются недостаточно освещенными отдельные аспекты задачи эффективного выбора инвестиционных проектов.

Изложение материала и его результаты

В мировой практике выделяют формы инвестиций в воспроизводство, такие как: новое строительство, расширение и реконструкция действующего предприятия, техническое перевооружение [6, c. 11].

Рассмотрим проблемы инвестирования в новое строительство и расширение производства. В 2017 г. благодаря росту мирового спроса и снижению китайского экспорта, а также за счет увеличения более чем на 8 % потребления стальной продукции внутри страны, черная металлургия пережила настоящее возрождение. Несмотря на это, по данным сайта Metaltorg.ru мировая загрузка металлургических мощностей к концу 2017 г. составила менее 70 %.

При такой загрузке производственных мощностей инвестирование в расширение производства является экономически необоснованным. По мнению финансового директора компании «Северсталь» А. Куличенко, нет смысла инвестировать в производственные мощности из-за чрезмерного производства стали в течение последующих нескольких лет как в глобальном масштабе, так и в России.

Однако данное утверждение не касается производств с высокой добавочной стоимостью. Магнитогорский металлургический комбинат инвестирует в Лысьвенский металлургический завод и планирует нарастить на нем в 2018 г. производство оцинкованной стали с полимерным покрытием в 2 раза. Из этого следует, что инвестирование в высокотехнологичное производство с высокой добавленной стоимостью оправдано.

Рассмотрим проблемы реконструкции и технического перевооружения предприятий. Отрасль металлургии требовала модернизации еще в 90-е годы. Но она не была проведена в связи с распадом Советского Союза и тяжелым этапом становления молодых государств. В настоящее время текущая модернизация предприятий происходит, потому что это неизбежный процесс, ведущий к сокращению производственных затрат, ослаблению нагрузки на окружающую среду, улучшению качества и освоению новых видов продукции.

Целая эпоха в металлургии закончилась с выводом из производства в марте 2018 г. последней, крупнейшей в России мартеновской печи на Выксунском металлургическом заводе. На данном этапе предприятие находится в процессе реконструкции: идет освоение центра финишной обработки труб, в конце года запускается цех по производству насосно-компрессорных труб, в планах – строительство производства бесшовных труб. Инвестиции в производство должны превысить 1 млрд долл.

В процессе модернизации Западно-Сибирского металлургического комбината (ЗСМК) предполагается осуществить перевооружение слябовой машины непрерывного литья заготовок, оптимизировать работу электросталеплавильного цеха, провести реконструкцию углеподготовительного цеха коксохимического производства и реконструировать разливочные мощности в доменном цехе. На осуществление задуманного в 2017– 2018 гг. ЗСМК инвестирует в предприятие 5 млрд рублей.

Новолипецкий металлургический комбинат в 2017 г. инвестировал в модернизацию производства 559 млн долл.

Обращают на себя внимание большие объемы финансирования инвестиционных проектов металлургических предприятий, влекущие за собой сложность в реализации. В связи с тем, что собственных средств, полученных за счет прибыли, и амортизационных отчислений для таких крупных проектов не достаточно, возникает необходимость в привлечении нескольких источников инвестиционных ресурсов для реализации одного инвестиционного проекта. В качестве источников могут выступать: заемное инвестирование (займы, поступающие от отечественных, иностранных, международных банков и других организаций, а также выпуск долговых ценных бумаг); акционерное инвестирование (вклады учредителей и стратегических инвесторов); централизованное инвестирование (средства государственного бюджета) и лизинг (вклад лизингодателей) [1, c. 230; 4].

Металлургия относится к числу зрелых отраслей, имеющих низкий уровень инвестиционной привлекательности, характеризуется большой инертностью (цикл «строительство – производство» зачастую превышает 10 лет), поэтому и не является приоритетным объектом вложения финансовых ресурсов для частных инвесторов [9, c. 65; 13, c. 7]. В связи с этим государство должно брать на себя решение задач, которые бизнес решить самостоятельно не может, содействовать инвестиционным процессам, происходящим в металлургической отрасли, и создавать дополнительные возможности для ее участников. Следует отметить огромную социальную значимость инвестирования в металлургические предприятия, так как в большинстве случаев они являются градообразующими, а также зависимость стратегических отраслей промышленности (ТЭК, ОПК, строительство и т. д.) от металлургии, что влечет заинтересованность государства в модернизации производства на собственной территории.

В процессе реконструкции металлургического предприятия обычно реализуется не один, а некая совокупность инвестиционных проектов. Поэтому перед руководством предприятия стоит задача выбора тех проектов (обычно в условиях дефицита инвестиционных ресурсов), которые позволяют получить максимальный экономический эффект и решить производственные, научнотехнические и экологические задачи [8, с. 278–279; 11, с. 224].

Предприятие должно провести оценку экономической целесообразности включения инвестиционного проекта в проектный портфель. Существует ряд методов, позволяющих рассчитать максимально допустимый объем инвестиционных ресурсов и сопоставить выгоду от реализации инвестиционных проектов с затратами, необходимыми для их реализации.

Для получения однозначных результатов сравнения проектов при их анализе рекомендуется в качестве главного критерия отбора использовать один из показателей экономической эффективности [2; 7; 10; 14], а именно – показатель чистой приведенной стоимости ( NPV ) [3, c. 262].

Из всего множества проектов Q выбираются те, при которых суммарный показатель NPV стремится к максимуму, а общие затраты не превышают выделенных финансовых ресурсов, то есть удовлетворяют условиям [5, с. 138]:

NPV^ = ^NVPj5j ^ max,(1)

j = 1

m

£ jj <Ф,(2)

j = 1

5 j = {0,1}, j = i?m,(3)

где NPV_j – чистая приведенная стоимость проекта j ; m – общее количество анализируемых проектов;

5 j - двоичная переменная. Отражает вхождение проекта j в перечень реализуемых проектов (проект j включается в число реализуемых, если 5 j = 1, и не включается - при 5 j = 0); I - финансовые затраты, необходимые для осуществления проекта j ; Ф – общий объем финансовых ресурсов, выделенных на реализацию портфеля проектов.

В работах по проектному анализу рекомендуется применять коэффициент выгоды-затраты (benefit-cost B/C) для решения задачи выбора портфеля реализуемых инвестиционных проектов в условиях ограниченных финансовых ресурсов [3, с. 97]:

nj

— = ^^1/ ( 1 + i ) ,        (4)

C j       t = 1

где Р j - норма прибыли j -го проекта; n j - срок реализации j -го проекта; i – коэффициент дисконтирования.

Необходимо упорядочить все проекты в порядке убывания данного показателя, а затем из полученного списка взять те, для которых суммарные инвестиционные затраты не превышают выделенные финансовые ресурсы.

Представленные выше основные подходы к решению задачи выбора проектов сводятся к двум методам: ранжирования и оптимизации.

Практическая реализация и сравнительный анализ указанных методов на примере решения прикладной задачи выбора инновационных проектов, реализуемых предприятием, осуществлялись на базе филиала № 12 ЗАО «Внешторгсервис».

Основные экономические характеристики рассматриваемых инвестиционных проектов филиала № 12 ЗАО «Внешторгсервис» представлены в таблице 1.

Произведем расчет показателей B/C (4) и NPV , который для проекта j рассчитывается по формуле (5) [5, с. 142]:

n j

NPV j = в j I j £ 1/ ( 1 + i ) t - I j , (5) t = 1

где I_j – объем инвестиций, необходимый для реализации проекта j .

Значение коэффициента дисконтирования i в расчетах принималось равным 0,1. Результаты вычислений для каждого из анализируемых проектов сведены в таблицу 2.

В таблицу 3 сведем величины объема необходимых инвестиций I_j и объема необходимых инвестиций накопительным итогом m

£ I j 5 j , а также критерии экономической эф- j = 1

фективности реализации выбранных проектов – величину NPV_j и величину NPV накопительным итогом NPV _Е . Упорядочим проекты по убыванию коэффициента выгоды-затраты B/C, используя метод ранжирования. В результате предложим рациональный вариант решения задачи выбора проектов, основываясь на ранжированном списке таблицы 3 и принимая условие независимости проектов.

Например, если для реализации всех проектов предприятия выделено 50 млн д. ед., то в число реализуемых проектов должны быть включены первые 9 проектов списка таблицы 3 (№ 2, 3, 4, 5, 7, 9, 10, 12, 15), так как общие затраты на их выполнение составляют 48,0405 млн д. ед. Отобранному портфелю проектов соответствует NPV ^ = 25 719,72 тыс. д. ед.

Улучшить полученное решение не возможно, так как оно является оптимальным с позиций критерия NPV _Е .

Однако не всегда использование метода ранжирования позволяет получить наилучшее решение задачи выбора инвестиционных проектов. Рассмотрим ситуацию, когда для осуществления проектов выделено 100 млн д. ед.

Согласно методике ранжирования должны быть выбраны те первые проекты списка, суммарные объемы финансирования которых

Таблица 1

Экономические параметры инвестиционных проектов филиала № 12 ЗАО «Внешторгсервис»

№ проекта	Объем необходимых инвестиций (тыс. д. ед.)	Средняя норма прибыли	Срок реализации проекта (годы)
1	6 416,93	0,32	4
2	2 491,06	0,36	7
3	4 307,81	0,32	6
4	4 606,94	0,35	6
5	3 941,93	0,41	5
6	25 569,70	0,20	8
7	5 173,94	0,23	15
8	5 541,51	0,27	7
9	2 055,89	0,22	14
10	6 834,36	0,23	12
11	19 199,25	0,21	8
12	12 906,53	0,20	13
13	17 000,00	0,23	8
14	7 035,47	0,27	6
15	5 721,50	0,23	10
16	4 987,19	0,19	12
17	27 264,77	0,18	15

Примечание. Рассчитано авторами по отчетности филиала № 12 ЗАО «Внешторгсервис».

не превышают заданной величины. В данном случае это проекты № 2, 3, 4, 5, 7, 8, 9, 10, 12, 15, 16 и 17. Общие затраты на финансирование этих проектов составляют 85,83397 млн д. ед., NPVΣ = 38 698, 27 тыс. д. ед. При этом из вы- деленных 100 млн д. ед. остаются неиспользованными более 14 млн д. ед.

Анализируя таблицу 3 можно увидеть, что полученное решение возможно улучшить, если в число реализуемых проектов добавить не про-

Таблица 2

Оценка эффективности инвестиционных проектов на основе показателей В/С и NPV

№ проекта	Величина показателя В/С	Величина показателя NPV
1	1,03	173,49
2	1,74	1 831,19
3	1,41	1 770,96
4	1,52	2 381,50
5	1,54	2 109,99
6	1,08	2 053,82
7	1,79	4 070,17
8	1,30	1 669,81
9	1,61	1 256,34
10	1,60	4 104,28
11	1,12	2 371,79
12	1,44	5 658,61
13	1,21	3 539,41
14	1,16	1 154,95
15	1,44	2 536,68
16	1,32	1 618,75
17	1,36	9 689,99

Примечание. Рассчитано авторами.

Таблица 3

Ранжирование проектов по показателю В/С

№ проекта	Величина показателя В/С	Объем необходимых инвестиций (тыс. д. ед.)	Объем необходимых инвестиций накопительным итогом (тыс. д. ед.)	Величина показателя NPV	Величина показателя NPV накопительным итогом
1	2	3	4	5	6
7	1,79	5 173,94	5 173,94	4 070,17	4 070,17
2	1,74	2 491,60	7 665,54	1 831,19	5 901,36
9	1,61	2 055,89	9 721,43	1 256,34	7 157,70
10	1,60	6 834,36	16 555,79	4 104,28	11 261,98
5	1,54	3 941,93	20 497,72	2 109,99	13 371,97
4	1,52	4 606,94	25 104,66	2 381,50	15 753,47
15	1,44	5 721,50	30 826,16	2 536,68	18 290,15
12	1,44	12 906,53	43 732,69	5 658,61	23 948,76
3	1,41	4 307,81	48 040,50	1 770,96	25 719,72
17	1,36	27 264,77	75 305,27	9 689,99	35 409,71
16	1,32	4 987,19	80 292,46	1 618,75	37 028,46
8	1,30	5 541,51	85 833,97	1 669,81	38 698,27
13	1,21	17 000,00	102 833,97	3 539,41	42 237,68
14	1,16	7 035,47	109 869,44	1 154,95	43 392,63
11	1,12	19 199,25	129 068,69	2 371,79	45 764,42
6	1,08	25 569,70	154 638,39	2 053,82	47 818,24
1	1,03	6 416,93	161 055,32	173,49	47 991,73

Примечание. Рассчитано авторами.

ект № 13, который непосредственно следует в списке за проектом № 8 (затраты на его реализацию значительно превышают 14 млн д. ед.), а проекты № 14 (объем финансирования 7 035,47 тыс. д. ед.) и проект № 1 (объем финансирования 6 416,93 тыс. д. ед.).

В результате суммарный показатель NPV реализуемых проектов увеличится на величину 1 328,44 тыс. д. ед. и составит 40 026,17 тыс. д. ед., а из выделенных 100 млн д. ед. остаются неиспользованными 0,71 млн д. ед.

Возможен и другой вариант улучшения исходного решения. Если из списка реализуемых проектов удалить проект № 8, а внести проект № 13, то показатель NPV _Σ реализуемых проектов составит 40 567,87 тыс. д. ед. (что выше предыдущего варианта), а из выделенных 100 млн д. ед. остаются неиспользованными 2,71 млн д. ед.

Заметим, что, как следует из таблицы 3, есть и другие варианты улучшения исходного решения. Таким образом, метод ранжирования инвестиционных проектов по убыванию удельного показателя их экономической эффективности не позволяет получить наилучшее решение задачи выбора инвестиционных проектов в условиях дефицита финансовых ресурсов.

Решим данную задачу методом оптимизации (1)–(3). В качестве значений коэффициентов NPVj целевой функции (1) должны рассматриваться величины показателя NPV проектов, приведенные в столбце 5 таблицы 3, а коэффициентам Ij ограничений (2) отвечают значения необходимых объемов финансирования отдельных проектов, содержащиеся в столбце 3. Параметру Ф можно придавать различные значения.

Результаты решения задачи (1)–(3) при различных объемах финансирования получены в Excel с помощью средства «Поиск решения» и представлены в таблице 4. В этой же таблице приведены аналогичные решения, но полученные методом ранжирования. Сравним решения, найденные различными методами.

При Ф = 100 млн д. ед. оптимальное решение имеет вид δ ₁ = 0, δ ₂ = 1, δ ₃ = 1, δ ₄ = 1, δ ₅= 1, δ ₆ = 0, δ ₇ = 1, δ ₈ = 1, δ ₉ = 1, δ ₁₀ = 1, δ ₁₁ = 0, δ ₁₂ = 1, δ ₁₃ = 1, δ ₁₄ = 0, δ ₁₅ = 1, δ ₁₆ = 0, δ ₁₇ = 1. Этому решению соответствует оптимальное значение целевой функции NPV _Σ = 40 618,9 тыс. д. ед.

Такие значения переменных δ _j означают, что при общем объеме финансирования проектов Ф = 100 млн д. ед. максимальное значение суммарной величины их показателей NPV будет получено при реализации инвестиционных проектов предприятия № 2, 3, 4, 5, 7, 8, 9 10, 12, 13, 15 и 17.

Сравнивая решения задачи выбора инвестиционных проектов двумя методами, отметим, что при одних объемах финансирования (Ф = 50, 80, 90 и 160 млн д. ед.) списки реализуемых проектов совпадают, а при других – отличаются. Например, при Ф = 100 млн д. ед. в списках проектов, полученных методом оптимизации, отсутствует проект № 16, но включен проект № 13. В результате суммарная ве-

Таблица 4

Решение задачи выбора проектов при различных объемах финансирования

Объем финансирования (млн. д. ед.)	Реализуемые проекты		Величина показателя суммарного NPV
	Метод ранжирования	Метод оптимизации	Метод ранжирования	Метод оптимизации
30	2, 4, 5, 7, 9, 10	2–5, 7, 9, 10	15 753,5	17 524,4
50	2-5, 7, 9, 10, 12, 15	2–5, 7, 9, 10, 12, 15	25 719,7	25 719,7
60	2–5, 7, 9, 10, 12, 15	2–5, 7–10, 12, 15, 16	25 719,7	29 008,3
70	2–5, 7, 9, 10, 12, 15	2–5, 7, 9, 10, 12, 17	25 719,7	32 873,0
80	2–5, 7, 9, 10, 12, 15, 17	2–5, 7, 8, 10, 12, 15, 17	35 409,7	35 823,2
90	2–5, 7–10, 12, 15–17	2–5, 7–10, 12, 15–17	38 698,3	38 698,3
100	2–5, 7–10, 12, 15–17	2–5, 7–10, 12, 13, 15, 17	38 698,3	40 618,9
120	2–5, 7–10, 12–17	1–5, 7–10, 12–17	43 392,6	43 566,1
140	2–5, 7–17	1–5, 7–17,	45 764,4	45 937,9
160	2–17	2–17	47 818,2	47 818,2

Примечание. Рассчитано авторами.

личина экономического показателя NPV выросла с 38 698,3 до 40 618,9 тыс. д. ед., то есть на 1 920,6 тыс. д. ед.

Еще более значительный рост показателя суммарного NPV при сравнении двух методов будет наблюдаться при других значениях общих объемов финансирования.

Например, как видно из таблицы 4, при Ф = 60 млн д. ед. и Ф = 50 млн д. ед. методом ранжирования выбран одинаковый перечень проектов. Использование оптимизационной модели при Ф = 60 млн д. е. позволяет включить в список реализуемых проектов дополнительно проекты № 8 и 16. Такому решению соответствует значение показателя эффективности NPV _Σ = 29 008,3 тыс. д. е., что превышает аналогичный показатель, полученный методом ранжирования, на 3 288,6 тыс. д. е.

Таким образом, проведенные расчеты показывают, что более предпочтительным является решение задачи выбора инвестиционных проектов с использованием математической модели (1)–(3). Этот подход сложнее, чем метод ранжирования проектов по некоторым показателям их эффективности, однако он позволяет получить лучшее решение рассматри- ваемой задачи (см. рисунок) и соответственно больший экономический эффект.

Попробуем еще усложнить задачу выбора проектов. Предположим, что инвестировать в проект № 7 будет целесообразно, если осуществляются подготовительные инвестиционные проекты № 1 и № 13 (например, запуск конвертера при увеличении мощности кислородного цеха и постройки воздуховода). Тогда математическая модель вида (1)–(3) будет дополнена следующим ограничением:

δ ₇ = δ ₁ = δ ₁₃.                (6)

При дополнительных ограничениях и объеме финансирования Ф = 90 млн д. е. проект № 7 выбывает из списка, несмотря на то, что при использовании метода ранжирования он стоит на первом месте, при этом дополнительно реализуется проект № 14. Такому решению соответствует значение показателя эф- оаебеам noe NPV _s = 35 783,0 тыс. д. е., что меньше аналогичного показателя, полученного без дополнительных ограничений на 2 915,3 тыс. д. е. (см. табл. 5).

Проект № 7 возможно реализовать, если объем финансирования увеличится до

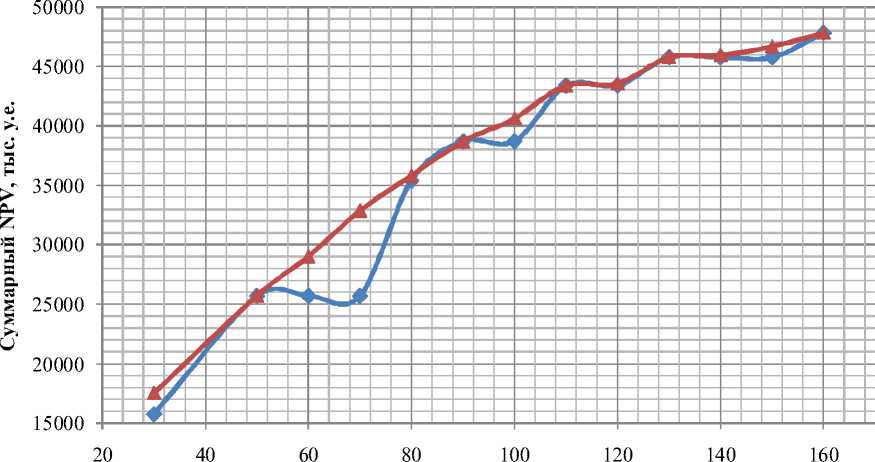
Объемы финансирования, млн у.е.

NPV рассчитан методом ранжирования          NPV рассчитан оптимизационным методом

Рисунок. Значения показателя суммарного для решения задачи выбора проектов, полученные различными методами

Примечание. Составлено по расчетам авторов.

Таблица 5

Решение задачи выбора проектов при различных объемах финансирования с дополнительными ограничениями

Объем финансирования (млн д. ед.)	Реализуемые проекты		Величина показателя суммарного NPV
	Метод оптимизации	Метод оптимизации с дополнительным ограничением	Метод оптимизации	Метод оптимизации с дополнительным ограничением
90	2–5, 7–10, 12, 15–17	2–5, 8–10, 12, 14– 17	38 698,3	35 783,0
100	2–5, 7–10, 12, 13, 15, 17	1–5, 7, 9, 10, 12, 13, 15, 17	40 618,9	39 122,6

Примечание. Рассчитано авторами.

Ф = 100 млн д. е. По сравнивнению с предыдущей ситуацией финансирования в этом случае появляются соответственно проекты № 1, 7 и 13, но отклоняются проекты № 8, 14 и 16.

Если провести сравнение с методом оптимизации без дополнительных ограничений при уровне финансирования Ф = 100 млн д. -ед., то появляется проект № 1 и отклоняется проект № 8. Это приводит к уменьшению значения показателя эффективности на 1 496,3 тыс. д. ед.

Проведенный анализ показал, что использование методов экономико-математического моделирования, в данном случае – применение оптимизационной модели, по сравнению с методом ранжирования позволяет получить более эффективное решение выбора инвестиционных проектов. Однако оптимизационная модель, обычно используемая для выбора инвестиционных проектов при ограниченности инвестиционных ресурсов, является в значительной степени идеализированной, не учитывает ряд важных аспектов осуществления реальных проектов. Это требует дальнейшей модернизации модели и внесения дополнительных ограничений.